動態結冰微觀孔隙結構定量分析

李偉斌，魏東，杜雁霞, *，易賢，楊肖峰

1.中國空氣動力研究與發展中心 空氣動力學國家重點實驗室, 綿陽 621000 2.中國空氣動力研究與發展中心 計算空氣動力研究所, 綿陽 621000

過冷水滴撞擊低溫基底在滿足一定條件后會發生凍結，隨著夾雜過冷水氣流的不斷撞擊，基底表面形成越來越厚的結冰。與傳統結冰較為不同的是，這種結冰具有典型的動態過程，在微觀上，表現為水滴的不斷凍結累積，并且相互間形成孔隙。由于結冰條件的不同，結冰微觀結構中的孔隙特性會存在不同程度差異，直接影響結冰的熱/力學特性。

在結冰冰形計算[1-2]中，結冰的密度是關乎冰形結果的重要參數；在結冰探測[3-4]中，波速與結冰的微觀結構密切相關；在防除冰模擬與試驗[5-6]中，黏附力、導熱系數等受結冰的致密程度影響。然而這些本質由結冰微觀孔隙結構決定的參數大多采用經驗設置方式給定，缺少定量化的手段，這極大限制了冰形精確預測、結冰高精度探測、防除冰系統的高效設計等。

目前，結冰微觀的定量研究多集中于晶核的形成、晶體生長、表面接觸形核等數值模擬[7-12]，雖然有利用孔隙率和分形維數等對結冰微觀結構進行定量刻畫[13-14]，但是缺少類似于多孔材料模型[15-17]的系統研究，無法實現對不同結冰條件下動態結冰孔隙的數學化表達。

本文針對動態結冰微觀孔隙結構定量研究的不足，以不同結冰條件下的結冰顯微圖像為對象，采用前期所提的變分分割模型[18-19]，對圖像中的孔隙進行分割提取，并分析了所使用分割方法的適用性；以孔隙提取結果為基礎，系統分析并提出了孔隙形態、孔徑分布等相關結構特征的數學表述方式。通過研究，以期為動態結冰微觀結構的數學模型建立提供理論依據和數據支撐。

1 結冰試驗手段及方法

1.1 結冰試驗

本文動態結冰試驗在中國空氣動力研究與發展中心(CARDC)小型結冰風洞中進行，其試驗段尺寸為0.3 m×0.2 m×0.65 m(寬×高×長)，如圖1所示。所使用的噴霧用水經過有效過濾，含雜質較少。試驗所用結冰模型為超臨界翼型剖面的縮比模型，弦長100 mm，展長200 mm，材料為7075鋁合金，導熱系數為130 W/(m·K)，如圖2所示。

圖1 0.3 m×0.2 m×0.65 m結冰風洞Fig.1 0.3 m×0.2 m×0.65 m icing wind tunnel

圖2 試驗模型Fig.2 Test model

1.2 結冰微觀圖像采集

結冰顯微圖像由電子顯微鏡連接電腦采集得到，顯微鏡型號為Olympus CX31，如圖3所示。由于基底表面和結冰表面的不同，動態結冰基底部分和其余部分具有明顯不同，本文主要討論動態結冰過程的微觀孔隙結構，為排除基底對結冰的影響，試驗結冰選取遠離基底的部分。結冰切片是低溫環境下從翼型結冰中切割而成，且表面處理光滑平整。文中試驗所使用的結冰顯微圖像均為40倍放大率下采集得到。

圖3 結冰顯微圖像采集系統Fig.3 Microscopy image acquisition system of icing

2 結冰微觀孔隙結構提取方法

結冰微觀結構的不同會直接影響結冰的熱/力學特性，開展結冰微觀孔隙結構提取是定量認識其變化規律的前提。

首先，采用前期所提變分分割方法[18]對結冰顯微圖像進行圖像處理，獲取孔隙的邊緣曲線。變分分割方法的做法是：① 提出分割思想，并將其數學化，最終得到相應的最小化問題；② 結合變分方法和水平集方法，應用優化方法對所提最小化問題進行求解。變分分割方法的求解初值為一條曲線，求解過程的中間量對應著演化曲線，所得到的解與最終的分割曲線對應。

定義u0:Ω→R為灰度圖像，Ω為矩形區域，表示圖像定義域，R為實數域。

文獻[18]的出發點是分割出圖像的背景部分，便可以得到需要的目標區域，即通過演化迭代得到一個足夠大的外部區域，并且該區域內的灰度值是相同的，它可以數學化表示為帶約束的優化問題,即

min -S(Ω1)

(1)

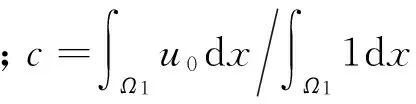
式(1)限制條件的目的是保證曲線外部灰度的同一性，但是由于自然圖像中背景部分的灰度值很難達到相同，因此采用Lagrange乘子法[20]對限制條件進行弱化，即

(2)

式中：μ>0為Lagrange乘子；l為區域Ω1的邊界長度，目的是減小圖像噪聲帶來的影響，即抑制噪聲點處產生小曲線，υ為其權重。

式(2)不能直接求解，需要將其數學化表示，應用水平集方法[21]，可以將演化曲線視為水平集函數φ的0-水平集，即集合{x|φ(x)=0}，將外部區域表達為：Ω1={x|φ(x)<0}，同時應用如下一維Heaviside函數，即

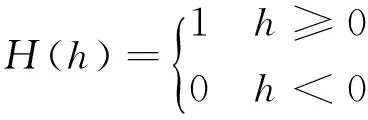
(3)

式中：h為自變量。便可最終得到與式(2)對應的最小化問題，即

(4)

關于φ對式(4)進行求導，可以得到其對應的Euler-Lagrange方程，再應用最速下降法，便可得到對應的水平集演化方程為

(5)

式中：δ(φ)為Dirac函數，僅在φ=0處有非零取值。因此在迭代求解式(5)時，兩個相鄰迭代步的值僅在φ=0處有較小變化，而φ=0對應著曲線的位置，也就是說兩個迭代步中的曲線位置變化較小，曲線演化速度較慢，這不利于曲線收斂至目標區域的邊界。為了克服δ(φ)對迭代過程帶來的影響，將其做近似處理，令δ(φ)≈1，最終得到求解的水平集演化方程為

(6)

求解式(6)，便可得到上述變分分割模型的收斂解φ*。基于此，可以得到孔隙的邊緣曲線C*={x|φ*(x)=0}及孔隙區域Ω*={x|φ*(x)>0}。進而結合MATLAB的bwlabel()和regionprops()等命令，對結冰中所有的孔隙進行編號，得到各自對應的面積和周長等相關定量信息。這樣就實現了結冰孔隙提取的目的。

3 動態結冰孔隙結構定量結果及分析

在結冰顯微圖像采集過程中，可見光從下至上，穿透結冰，并進入顯微鏡鏡頭部分，從而使成像系統清晰捕捉結冰的放大圖像。由于這一成像特點，使得光線經過結冰的氣泡孔隙時，發生折射現象，從而在所成圖像中呈現出黑色散斑。在結冰微觀研究中，孔隙分布的相關特性是分析工作的基礎。本文開展了不同溫度下的結冰微觀孔隙結構定量分析研究工作，其中水滴平均粒徑MVD=38 μm，液態水含量LWC=0.75 g/m3，速度v=25 m/s，溫度T在試驗分析中給出。

3.1 動態結冰顯微圖像分割結果

圖4 閾值法和變分分割方法分割結果對比Fig.4 Comparisons of segmentation results by thresholding and variational methods

為了驗證本文分割方法的優越性，將其與傳統的閾值法進行了分割效果對比，結果展示于圖4中。閾值法是以某一給定像素值為閾值，將待分割區域二值化，從而得到分割結果。本試驗中，選擇的是彩色圖像的第3通道作為分割對象，為了對比的統一性和展示效果，將閾值法的二值化結果轉換為類似于變分分割方法的分割曲線形式。閾值法的關鍵在于閾值的選擇，圖4(a)～圖4(c)給出了3個閾值的分割結果。由于光線傳播的特點，某些孔隙中部會顯示出亮點，無論閾值如何選擇，都沒能正確分割孔隙，即將孔隙內部從孔隙中分離出，沒有得到完整孔隙(見圖4中白色框對比結果)，并且閾值選擇不恰當會將焦平面外的孔隙分割出，得到不正確的分割區域，進而直接影響孔隙分布規律的分析結果。而本文分割方法得到了較為準確的分割結果，如圖4(d)所示。

結冰條件的不同會直接導致結冰顯微圖像內孔隙大小和數量的不同，為了研究它們的變化規律，開展了不同溫度條件下的結冰試驗，并應用變分圖像分割方法，對它們的顯微圖像進行了分割處理，結果如圖5所示。從結果可以看出，每個狀態下的孔隙均被有效分割出，并且孔隙形狀與圓形較為接近。同時，從結果可以發現孔隙數量、大小和分布確實存在著明顯不同。

圖5 不同溫度的顯微圖像分割結果Fig.5 Segmentation results of microscopic images with different temperatures

3.2 動態結冰孔隙形態

動態結冰內部孔隙的形態是對微觀結構進行合理數學建模并分析其結構特征的基礎，應用第2節的變分分割方法對動態結冰顯微圖像進行分割處理，討論孔隙形態。采用式(7)的圓形度表征量[22]對結冰孔隙的截面形狀進行分析，即

C=4πA/L2

(7)

式中：A和L分別為孔隙截面的面積和周長；C值表征的是區域近似于圓形的程度。顯然，當區域為圓時，式(7)具有最大值1。當區域越近似于圓，值越趨近于1；當區域越復雜，C值越小。圖6中給出了同一放大倍數下，不同溫度、不同結冰區域微觀圖像中的孔隙截面對應的C值，其中橫坐標n為孔隙序號。同時表1中給出了C值的相關統計信息。從表中數據可以看出，結冰中C>0.785 4(正方形)的區域占比較大，且所有C值的均值和中值均接近于1，即大多數孔隙截面近似于圓形，這點也可以從圖5的分割結果和動態結冰過程孔隙受力情況中得到驗證。基于此，結合顯微圖像采集的廣泛性及隨機性，可以推廣得到孔隙任意截面均為圓形的結論。因此，在對結冰微觀結構進行量化描述過程中，將結冰孔隙視為球形是可行的。

圖6 結冰孔隙截面圓形度Fig.6 Circularity of pores cross-section of icing

表1 圖6數據的統計信息Tabel 1 Statistical information of data in Fig.6

總個數C>0.7854的個數/占比C均值C中值321240/0.74770.83240.8815

3.3 動態結冰孔隙孔徑分布

從圖5可以看出不同溫度下的孔隙孔徑的分布特性存在著明顯不同，為了更清楚認識這種不同，對其進行定量分析。在孔隙呈球形的結論之上，考慮其區域的復雜性，基于面積和周長數據，通過式(8)計算動態結冰中不同孔隙的直徑:

(8)

對大量孔隙直徑進行統計，圖7給出了不同區間無量綱孔徑頻率f的直方圖。從圖中可以看出，在一定區間范圍內，孔隙直徑均完全覆蓋，即其可以取一定范圍內的任意值。理論上，在結冰過程中，主要受結冰熱/力學的影響，孔隙的形成具有隨機性，并且其大小可以為任意實數。因此，孔隙孔徑的取值是連續的。

從圖7中可以看出不同孔徑的分布密度是不同的，為了更清晰、量化認識這種不同，基于結冰顯微圖像的分割結果，計算直徑的分布函數F(d)，并應用式(9)對其進行曲線擬合，即

(9)

式中：k1、k2均為正實數；x∈[0,+∞)。圖8給出了不同溫度條件下的直徑分布函數和擬合函數對應的曲線圖(參數k1、k2的取值見表2)，從圖中可以看出所有擬合曲線與孔徑分布函數吻合較好。因此，孔隙的孔徑分布函數可以用式(9)的形式表達。進而，結合孔隙孔徑取值是連續的結論，可以推導其概率密度函數(Probability Density Function, PDF)為

圖7 結冰孔隙直徑的頻數直方圖Fig.7 Frequency histogram of pore diameters of icing

圖8 結冰微觀孔徑分布曲線及其擬合曲線Fig.8 Distribution curves of micro pore diameter of icing and the fitting curves

(10)

圖9中給出了圖8對應狀態的概率密度函數擬合曲線圖，可以看出隨著溫度的降低，孔徑最大值增大，概率密度峰值減小。這是因為在保持其他結冰條件不變的情況下，溫度越低，過冷水滴撞擊基底表面結冰速率更快，溢流效應減弱，水滴之間以及水滴與結冰之間夾雜的氣泡更不易破碎或者逃逸。

式(9)是所提出的關于孔徑的分布函數，其在不同結冰條件下的參數取值(k1,k2)不同。為了驗證該形式在同一結冰狀態下的適用性，分別選取溫度為-4.8 ℃和-11 ℃動態結冰不同位置的結冰，進行微觀孔徑分布分析，結果展示于圖10中。從圖中可以看出，同一結冰條件不同結冰位置的孔徑分布與所提出的分布函數具有較好的吻合度，說明以式(9)和式(10)定量表征結冰孔徑分布規律是可行的。

表2 圖8中擬合函數參數取值Tabel 2 Parameter values of fitted functions in Fig.8

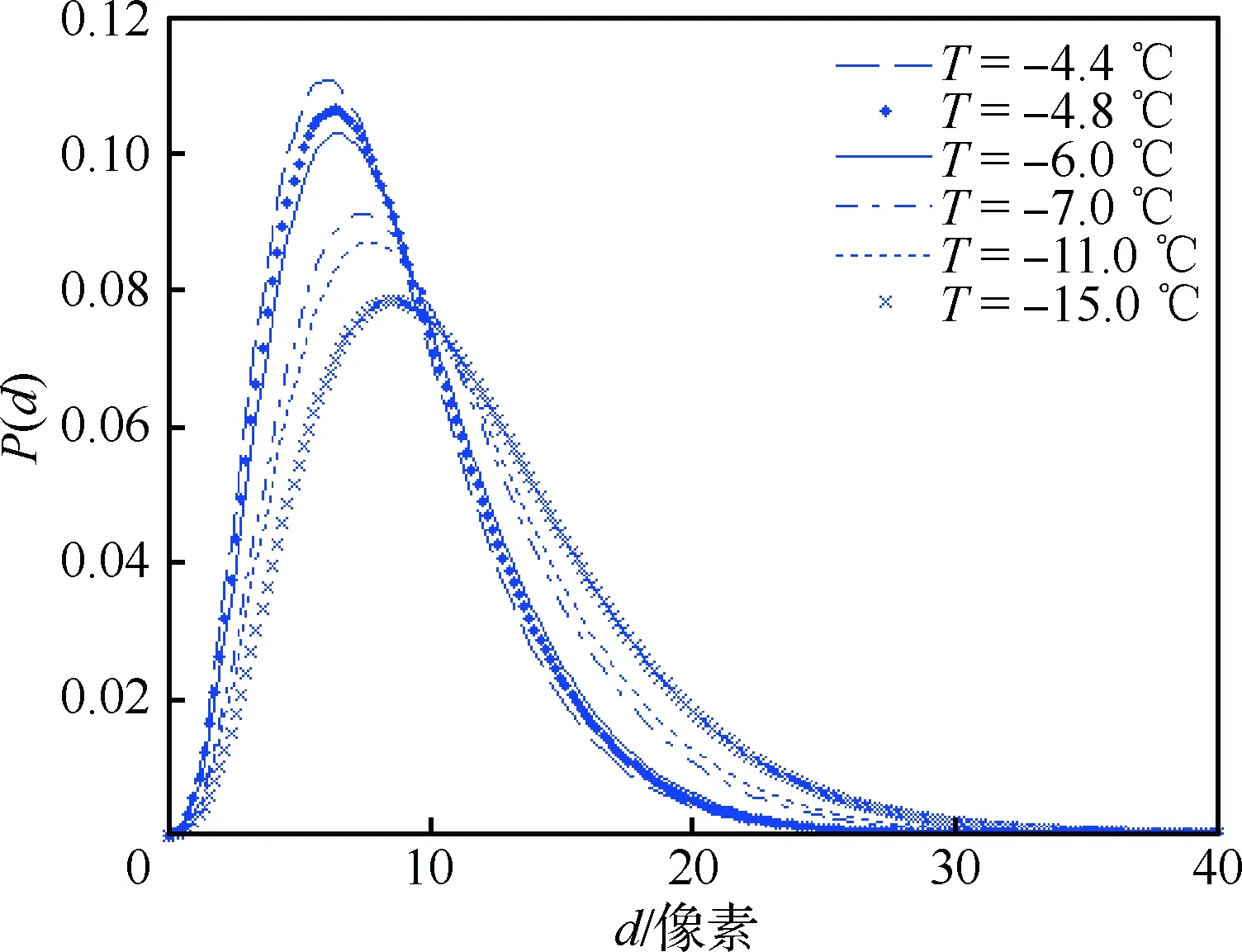
圖9 結冰微觀孔徑概率密度函數擬合曲線Fig.9 Fitted PDF curves of micro pore diameter of icing

圖10 多位置結冰微觀孔徑分布曲線及 其擬合曲線Fig.10 Distribution curves of micro pore diameter of icing on different locations and the fitting curves

4 結 論

1) 在結冰微觀孔隙提取方面,相比于傳統方法，文中使用的變分分割方法能夠得到更準確的分割結果，能夠保持孔隙的完整性，對結冰微觀結構的定量分析提供了較好的數據輸入。

2) 在結冰微觀孔隙結構定量研究方面。通過對結冰內部大量孔隙形態、直徑等相關信息進行統計分析，可以得到微觀孔隙近似呈球形、孔徑分布連續等結論。并在此基礎上提出孔徑分布函數表達式，試驗結果表明所提表達式與結冰內部孔隙孔徑分布較為吻合。

本文對動態結冰孔隙形態和孔徑的分布進行了初步的定量分析討論，下一步將基于更完整的結冰風洞試驗數據，定量確定參數k1和k2與結冰條件的關系，進而建立動態結冰三維結構數學模型，提取用于表征其微觀特征的定量指標，最終建立結冰微觀與宏觀間的聯系。

[1] MESSINGER B L. Equilibrium temperature of an unheated icing surface as a function of airspeed[J]. Journal of the Aeronautical Sciences, 1953, 20(1): 29-42.

[2] MYERS T G, CHARPIN J P F. A mathematical model for atmospheric ice accretion and water flow on a cold surface[J]. International Journal of Heat and Mass Transfer, 2004, 47 (25): 5483-5500.

[3] IKIADES A A, KONSTANTAKI M， CROSSLEY S D. Fiber optic sensors technology for air conformal ice detection[C]∥Optical Technologies for Industrial, Environmental, and Biological Sensing. International Society for Optics and Photonics, 2004: 357-368.

[4] 尹勝生, 葉林, 陳斌, 等. 可識別冰型的光纖結冰傳感器[J]. 儀表技術與傳感器, 2012(5): 9-12.

YIN S S, YE L, CHEN B, et al. Fiber-optical icing sensor for detecting the icing type[J]. Instrument Technique and Sensor, 2012(5): 9-12 (in Chinese).

[5] IVALL J, RENAULT-CRISPO J S, COULOMBE S, et al. Ice-dependent liquid-phase convective cells during the melting of frozen sessile droplets containing water and multiwall carbon nanotubes[J]. International Journal of Heat and Mass Transfer, 2016, 101: 27-37.

[6] KEITZL T, MELLADO J P, NOTZ D.Impact of thermally driven turbulence on the bottom melting of ice[J]. Journal of Physical Oceanography, 2016, 46(4): 1171-1187.

[7] YE Y, NING N, TIAN M, et al. Nucleation and growth of hexagonal ice by dynamical density functional theory[J]. Crystal Growth & Design, 2017, 17(1): 100-105.

[8] BLAKE J, THOMPSON D, RAPS D, et al. Simulating the freezing of supercooled water droplets impacting a cooled substrate[J]. AIAA Journal, 2015, 53(7): 1725-1739.

[9] LU Y, ZHANG X, CHEN M. Size effect on nucleation rate for homogeneous crystallization of nanoscale water[J]. The Journal of Physical Chemistry B, 2013, 117(35): 10241.

[10] COX S J, RAZA Z, KATHMANN S M, et al. The microscopic features of heterogeneous ice nucleation may affect the macroscopic morphology of atmospheric ice crystals[J]. Faraday Discussions, 2013, 167(1): 389-403.

[11] ZHANG X X, LU Y J, CHEN M. Crystallisation of ice in charged Pt nanochannel[J]. Molecular Physics, 2013, 111(24): 3808-3814.

[12] LUPI L, HUDAIT A, MOLINERO V. Heterogeneous nucleation of ice on carbon surfaces[J]. Journal of American Chemical Society, 2014, 136(8)：3156-3164.

[13] LEI G L, DONG W, ZHENG M, et al. Numerical investigation on heat transfer and melting process of ice with different porosities[J]. International Journal of Heat and Mass Transfer, 2017, 107: 934-944.

[14] 杜雁霞, 桂業偉, 柯鵬, 等. 飛機結冰冰型微結構特征的分形研究[J]. 航空動力學報, 2011, 26(5): 997-1002.

DU Y X, GUI Y W, KE P, et al. Investigation on the ice-type microstructure characteristics of aircraft icing based on the fractal theories[J]. Journal of Aerospace Power, 2011, 26(5): 997-1002 (in Chinese).

[15] FRANK C. Reservoir formation damage: Fundamentals, modeling, assessment and mitigation[M]. 2nd ed. Burlington: Gulf Professional Publishing, 2007.

[16] LEHMANN P, STAHLI M, PAPRITZ A. A fractal approach to model soil structure and to calculate thermal conductivity of soils[J]. Transport in Porous Media, 2003, 52(3): 313-332.

[17] OKABE H, BLUNT M J. Pore space reconstruction of vuggy carbonates using microtomography and multiple-point statistics[J]. Water Resources Research, 2007, 43(12): W12S02.

[18] LI W B, YI X, SONG S H. Convex background removed model for image segmentation using the split Bregman method[J]. Journal of Information and Computational Science, 2015, 12(17): 6641-6652.

[19] 李偉斌, 易賢, 杜雁霞, 等. 基于變分分割模型的結冰形測量方法[J]. 航空學報, 2017, 38(1): 120167.

LI W B, YI X, DU Y X, et al. A measurement approach for ice shape based on variational segmentation model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 120167 (in Chinese).

[20] BERTSEKAS D P. Constrained optimization and Lagrange multiplier methods[M]∥Computer Science and Applied Mathematics. Boston: Academic Press, 1982: 1.

[21] OSHER S, FEDKIW R. Level set methods and dynamic implicit surfaces[M]. New York: Springer-Verlag, 2002: 51-72.

[22] 王東霞, 宋愛國. 基于三坐標測量機的圓度誤差不確定度評估[J]. 東南大學學報(自然科學版), 2014, 44(5): 952-956.

WANG D X, SONG A G. Uncertainty assessment of circularity error based on coordinate measuring machine[J]. Journal of Southeast University (Natural Science Edition), 2014, 44(5): 952-956 (in Chinese).