S形進氣道錘激波的動態特性

劉庭申，馮立好，王晉軍

北京航空航天大學 航空科學與工程學院，北京 100083

進氣道的錘激波載荷由發動機強喘振引起。發動機喘振主要由壓氣機葉片的部分或全部失速所產生，可導致進入發動機的流量突然減少，同時伴隨著發動機進口壓力的急劇升高。這種壓力的突變會產生向上游傳播的壓力波，一般稱為錘激波。錘激波的峰值壓力遠遠大于定常狀態的壓力值，通常能達到定常值的兩倍以上。因此盡管錘激波現象并不常見，錘激波載荷卻是飛機進氣道結構強度設計的決定性因素之一[1]。如果進氣道的結構強度無法承受錘激波載荷的沖擊，發動機出現喘振時可能會導致進氣道的破壞，進而威脅飛機的飛行安全。如果進氣道結構強度設計過于保守，則會使得進氣道重量太大影響到飛機的性能。所以，對進氣道錘激波現象進行研究，獲得較為準確的進氣道錘激波載荷具有非常重要的價值。

國外已經進行了一些關于進氣道錘激波現象的研究。一些研究者采用試驗方法探究了飛機進氣道的錘激波現象[1-6]，通過各種方法誘使發動機喘振，進而進行數據的測量。Marshall[2]依據大量的試驗測量數據總結了發動機喘振時壓力變化過程以及喘振超壓的估算方法，可以在只做較少次數的發動機喘振試驗的情況下估算多種不同狀態的發動機喘振壓升情況，為進氣道的錘激波研究提供了基礎。Nugent和Holzman[5]對F-111A飛機進行飛行試驗，獲得了多種飛行狀態下發生喘振時發動機和進氣道壓力隨時間變化情況以及錘激波的傳播速度等數據。在數值計算方面，早期的研究主要針對二維管道開展[7-8]。Hindash等[7]通過對二維管道的錘激波模擬分析了進氣道的受載情況并與試驗數據對比驗證了計算的準確性，同時文章進一步分析了進氣道出口不均勻壓升產生的錘激波的傳播特點以及不同進氣道幾何形狀對錘激波傳播過程的影響。

此后一些學者陸續進行了三維數值模擬研究，并且應用到了多種戰斗機進氣道錘激波現象的研究中[9-12]。Goble等[9]進行了F-22飛機進氣道的錘激波三維數值模擬研究，他們采用在進氣道出口設定隨時間變化的壓力作為邊界條件來產生錘激波，計算了多種飛行條件下的錘激波情況，總結了進氣道所受的壓力分布規律，并發現了進氣道的支路和抽吸孔排氣可以降低進氣道所受的錘激波峰值壓力。類似的錘激波模擬方法應用到了瑞典JAS-39飛機的進氣道錘激波研究中[10]，作者討論了動態計算時間步長的選取，以及加快計算速度的方法，探討了不同計算模型在計算速度和準確性方面的優劣。根據計算結果獲得了進氣道壁面的錘激波載荷數據，并為飛機的進氣道強度設計提供了依據。數值方法的應用可以較為準確地獲得進氣道所受錘激波壓力的分布情況，為進氣道結構強度設計提供更豐富的信息。Gridley等[13]進一步提出了將不同飛行狀態的錘激波載荷和各狀態出現的概率相結合的方法，允許在小概率情況下出現錘激波載荷超出進氣道結構設計強度，從而進一步降低進氣道的結構重量。

國內關于進氣道錘激波載荷的相關文獻較少。主要由朱宇和沈天榮[14]歸納總結了國外錘激波載荷的研究方法和成果，而關于試驗和數值計算的研究成果很少。目前，國內主要采用工程估算的方法評估發動機喘振超壓比，以此作為進氣道錘激波載荷。與此同時，如果能輔以數值模擬計算錘激波沿管道運動過程中載荷變化情況，可以更加有效地為進氣道的結構設計提供幫助。

雖然國外已經對錘激波現象進行了一些研究，但是大部分只提供了進氣道壁面壓力分布，較少關注錘激波過程中進氣道內部的流動結構變化，尤其是內部復雜的三維流動特性。本文對進氣道錘激波進行研究，探討適用于進氣道錘激波計算的三維非定常數值模擬方法，獲得錘激波傳播過程中進氣道壁面壓力變化情況，并且對進氣道內部的三維流動結構和動態演化過程進行分析總結。

1 模型和計算方法

本文采用的計算模型為M2129型S形進氣道。這是一種圓形截面進氣道。它由AGARD(Advisory Group for Aerospace Research and Development)設計，并進行了風洞試驗[15]。試驗在來流馬赫數為0.21下進行，包含了兩種不同的流量條件，兩種流量下喉道的馬赫數分別為0.412和0.794。試驗所測得的進氣道壁面上的壓力分布數據可以獲得，經常被用于數值模擬結果的驗證對比[16-18]。

M2129型S形進氣道的剖面幾何形狀見圖1。該進氣道模型包括外部壁面、筆直的入口段和出口段，以及中間的S段。為了接近常見飛行器的進氣道尺寸，本文中的進氣道模型尺寸相比于原試驗中的模型擴大了4.65倍。其入口段的直徑為0.6 m，出口段直徑約為0.7 m，入口段長度為0.6 m，中間S段的中軸線長度為2.184 m。由于模型是對稱的，僅選取了一半的結構進行計算。為了記錄進氣道壁面壓力隨時間的動態變化，選取了上下壁面各11個點進行記錄，即P1～P11和S1～S11。22個點的編號和位置也在圖1中標出，第1個點同進氣道入口的距離和后面每相鄰兩個點沿x方向的距離均為0.3 m。

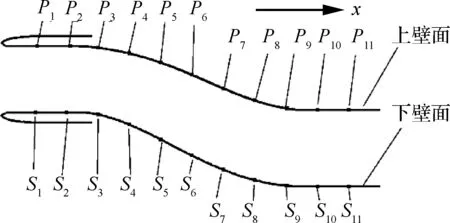
圖1 M2129型S形進氣道幾何模型Fig.1 M2129 S-shaped inlet geometry model

圖2 進氣道壁面網格劃分Fig.2 Grid distribution on inlet wall

整個計算域使用結構網格進行劃分，進氣道壁面上網格如圖2所示。為了精確模擬進氣道內部的流動，進氣道內部流場采用了較密的網格。近壁面的網格也進行了加密來模擬壁面流動。網格數量一共約200萬。

本文采用非定常雷諾平均Navier-Stokes方程進行數值計算，采用耦合求解器求解。外流場設定為壓力遠場邊界條件，給定來流的馬赫數和靜壓，在進氣道出口給定反壓。首先采用定常計算的方法獲得初值，再在進氣道出口給定壓力隨時間變化的函數來模擬發動機喘振的壓力變化，進而進行錘激波的動態計算。這種錘激波的數值模擬方法將在后文中詳細介紹。動態計算的時間步長為2.5×10-5s。計算所選用的湍流模型為k-ε模型。這種湍流模型已經由Nichols[16]在M2129型進氣道模型上進行了靜態的計算，并與試驗結果對比驗證了正確性。

本文為了驗證計算的準確性，將風洞試驗數據和計算所獲得的結果進行了對比。試驗數據來自文獻[15]。因為試驗的低流量狀態和后面用于錘激波計算的流量狀況比較接近，選取該狀態的試驗數據進行對比驗證。

試驗條件是來流馬赫數為0.21，進氣道喉道處的馬赫數為0.412，雷諾數為1.158×106。圖3為試驗和計算獲得的進氣道上下壁面的壓力分布結果，圖中橫坐標為各點x坐標與該方向總長度L的比值，縱坐標為靜壓p與來流總壓pt的比值。上壁面壓力的計算結果與試驗數據非常吻合，下壁面計算結果數值略高于試驗數據，但是誤差在3%以內。表明本文所用方法可以對M2129型進氣道內部的流動情況進行準確的模擬。

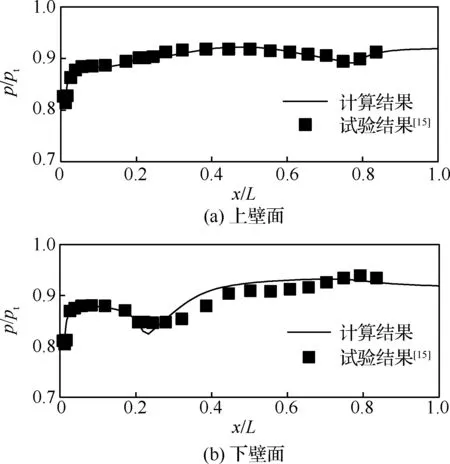
圖3 進氣道上下壁面壓力計算與試驗結果對比Fig.3 Comparison between numerical and experimental results of inlet upper and lower walls

為進一步驗證非定常計算的準確性，對激波管問題進行了數值模擬，并與理論解進行了比較，計算所用激波管長度為1 m，均分為等長的高壓段和低壓段，之間由薄片隔開。高壓段壓力為1 Pa，密度為1 kg/m3。低壓段壓力為0.1 Pa，密度為0.125 kg/m3，計算從兩段氣體之間的薄片突然撤離開始。圖4為時間t=0.2 s時激波管內的壓力p、密度ρ、速度v分布情況的計算結果和理論值的對比。結果表明本文所用數值方法可以準確地模擬激波傳播的非定常過程。

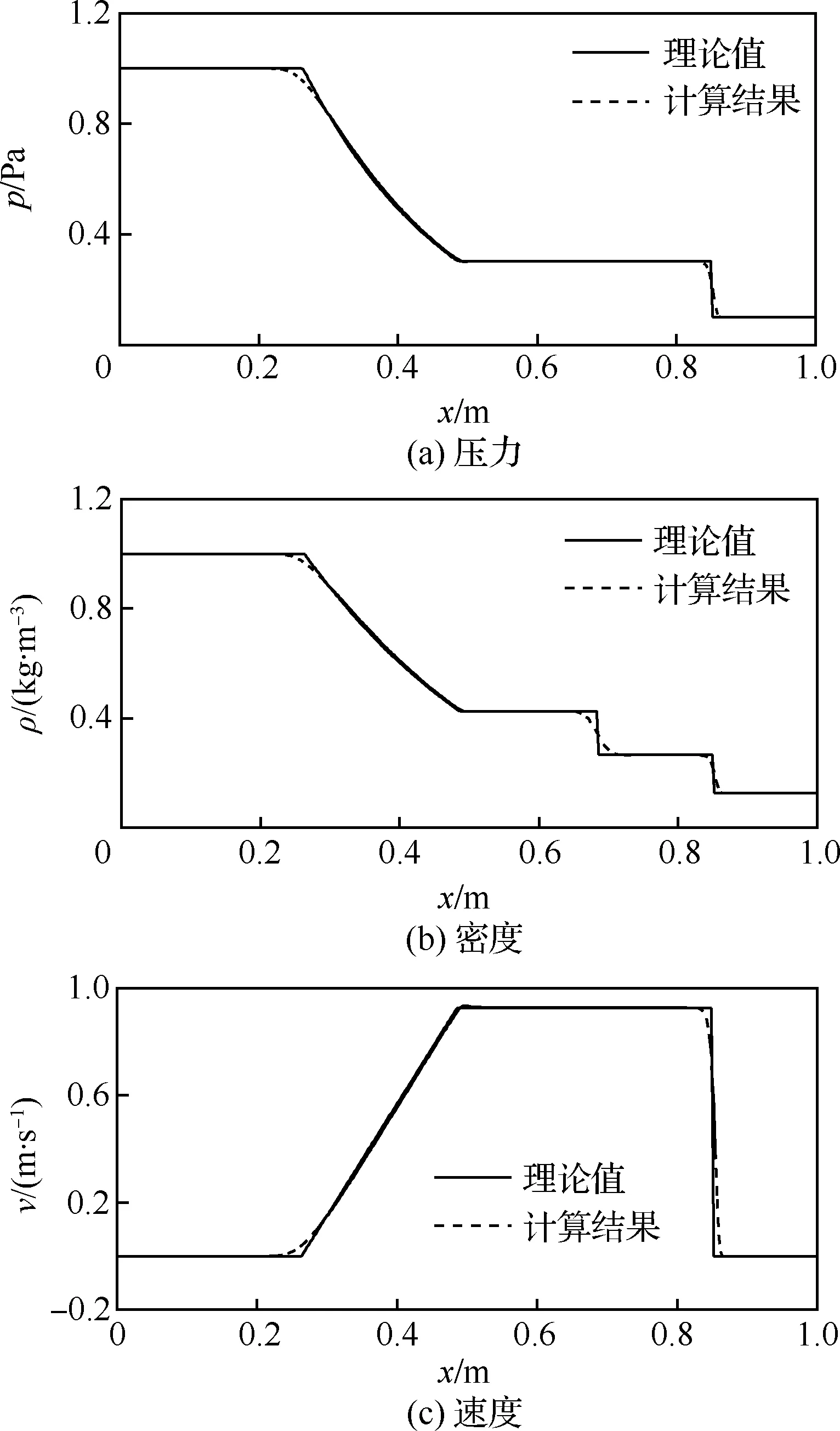
圖4 激波管內壓力、密度和速度的數值與理論結果對比Fig.4 Comparison of pressure,density and velocity between numerical and theoretical results of shock tube

2 錘激波波形設置

通常所采用的計算方法是直接給定喘振時的壓力變化波形作為邊界條件[7-11]，進一步進行錘激波的計算，本文采用同樣的方法。壓力波形的確定依賴于發動機喘振的實際測量數據，不同發動機發生喘振時可能會有不同的壓力變化波形。波形的差異會影響錘激波的計算結果，因此應當盡量準確地模擬實際的壓力變化情況。

通過對喘振時發動機壓力波形的試驗測量發現不同的發動機型號以及不同的喘振狀況產生的壓力變化波形會有所差異。但是其隨時間變化規律通常為迅速達到峰值之后緩慢地下降[7]。因此本文選用圖5所示三角形波形進行錘激波的數值模擬，其超壓比為2.1，即峰值壓力為定常值的2.1倍。出口壓力一開始保持恒定，在t=0.01 s時瞬間達到峰值。之后壓力呈線性下降，經過0.1 s，即在t=0.11 s時壓力恢復到初始值。在此之后，壓力保持不變，直到計算結束。這種波形的壓力曲線如圖5所示，圖中縱坐標為各時刻壓力同定常時壓力pss的比值。

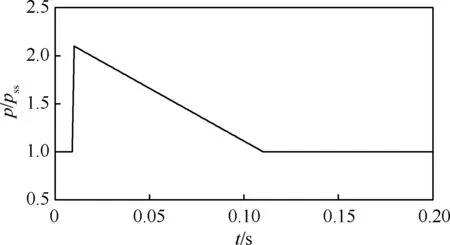
圖5 錘激波壓力波形Fig.5 Pressure waveform of hammershock

3 壓力變化與流動結構

本節進行錘激波計算的狀態為來流馬赫數Ma∞=0.65，來流靜壓p∞=101 325 Pa，靜溫T∞=288.15 K，進氣道定常時的換算流量Wc=60 kg/s(即進氣道出口馬赫數Mae=0.44，入口馬赫數Ma0=0.63)。進氣道上下壁面各點靜壓隨時間變化記錄在圖6中。各點所對應的位置已經在圖1中顯示，圖中將各點的靜壓值除以來流靜壓p∞從而進行無量綱處理。圖6(a)為上壁面各點的結果，圖6(b)為下壁面各點的結果。從圖中可以明顯地看出沿著進氣道入口到出口各點壓力曲線的變化規律。

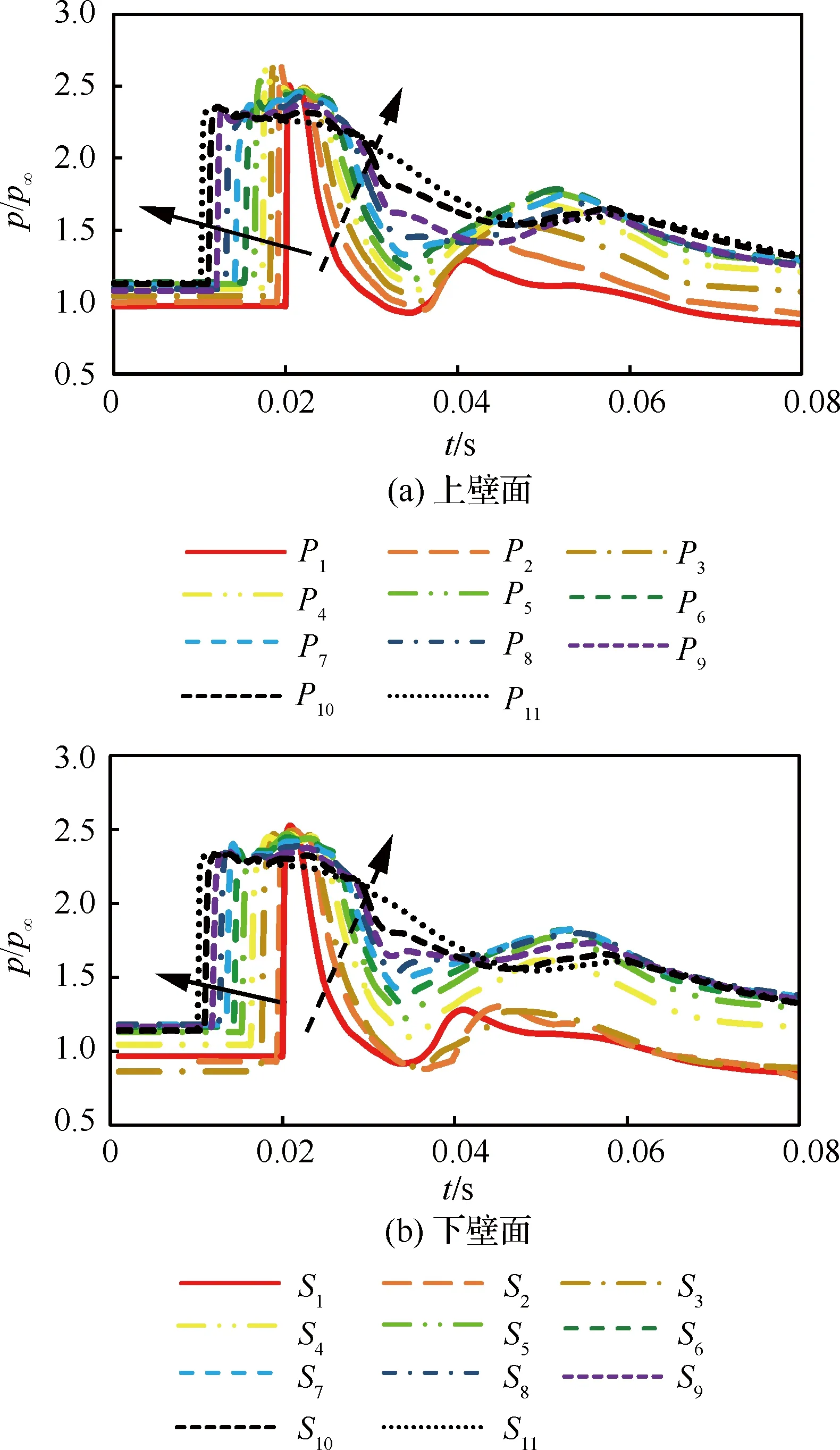
圖6 進氣道上下壁面壓力隨時間變化曲線Fig.6 Time history of pressure on inlet upper and lower walls

圖6(a)中沿實線箭頭方向依編號次序逐個經過P1～P11的曲線，說明越靠近進氣道出口的點壓力開始升高的時間越早，反映了錘激波沿著進氣道逐漸向上游傳播的過程。觀察圖6(a)中壓力曲線在達到峰值之后的下降段，從P1～P11各點的曲線也沿著虛線箭頭方向排布，表明越靠近進氣道出口的點，壓力達到峰值之后下降得越慢。由于該種變化規律，使得曲線的形態呈現出越靠近進氣道入口的點的曲線顯得更尖，而越接近進氣道出口的點的曲線更寬。關于下壁面的點S1～S11，圖中箭頭也標示出了相似的變化規律。根據最靠近進氣道入口的點P1和S1的壓力達到峰值的時間，可計算出錘激波在進氣道內移動的平均速度為306 m/s，馬赫數約為0.9。而錘激波相對于上游來流的平均傳播速度為481 m/s，馬赫數達1.42。

圖7統計了上下壁面各11個點的峰值壓力和定常時的壓力值。可以看到總體上靠近入口位置的載荷略大于出口附近載荷，最大峰值壓力位于上壁面靠近入口的彎折處。上下壁面各點的峰值壓力均達到來流靜壓的2.3～2.65倍左右，說明錘激波能夠誘導產生比定常狀態更高的載荷。

圖7 進氣道上下壁面峰值壓力和定常狀態壓力Fig.7 Peak pressure and steady pressure on the inlet upper and lower walls

圖8顯示了錘激波經過進氣道時壁面上的壓力同來流靜壓比值(p/p∞)的分布云圖；圖9為上下壁面沿程壓力分布曲線，從圖中可以看到錘激波沿進氣道向上游傳播時壓力變化的過程。圖8(a)為t=0.01 s時的壓力云圖，此時進氣道出口壓力剛產生突變，在進氣道壁面上還未產生明顯的影響。在t=0.015 s時，即圖8(b)所示，錘激波剛經過進氣道的第1個彎折處，此時錘激波位置的下壁面受到的壓力略高于上壁面。在t=0.017 5 s和t=0.02 s兩個時刻，即圖8(c)和圖8(d)所示，錘激波正經過進氣道第2個彎道，此時可以明顯看出錘激波處上壁面的壓力較高。由圖8所示的壓力云圖可以發現，錘激波向上游傳播的過程中進氣道受到的最大壓力的區域位于進氣道入口附近彎折處的上壁面，這一區域所受峰值壓力達到來流靜壓的2.65倍左右。在錘激波傳出進氣道之后，進氣道出現了中部壓力較高，入口和出口附近壓力較低的特點，如圖8(e)所示。在這一中部高壓區逐漸后移并消散之后，進氣道便呈現出越靠近入口壓力越低的特點。

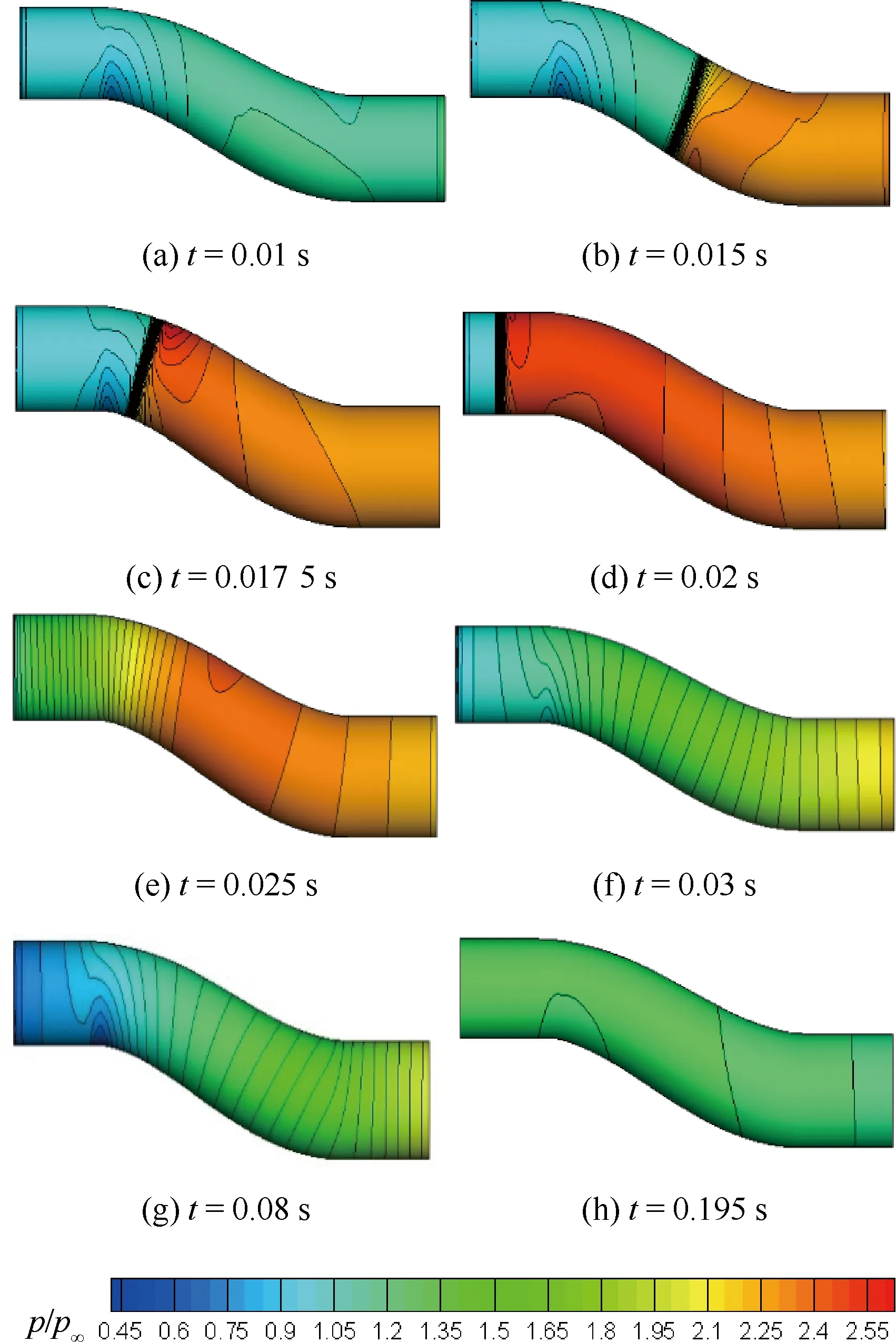
圖8 進氣道壁面壓力云圖Fig.8 Pressure contours on inlet wall

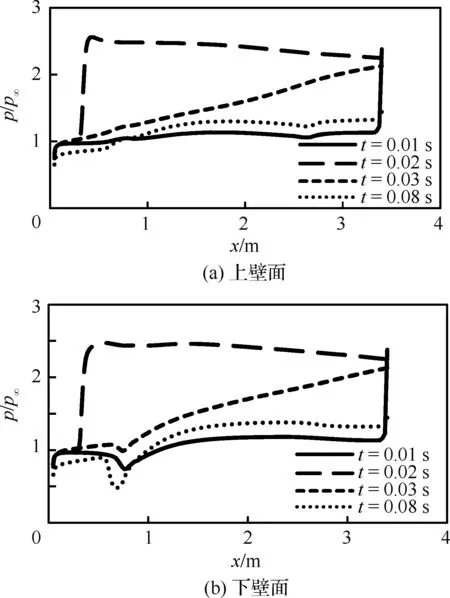
圖9 進氣道上下壁面沿程壓力分布Fig.9 Pressure distribution along inlet upper and lower walls

對于圖9所示壓力沿程分布曲線。在t=0.01 s時剛剛產生錘激波，因而可以看到相應時刻曲線在出口處(x=3.4 m)壓力突增，而其他部位的壓力分布與穩態時相同。在t=0.02 s時，錘激波傳至進氣道入口附近。可以看到，在激波面下游，上下壁面壓力沿進氣道軸向以相近的梯度逐漸下降，與所設定的錘激波波形的形態類似。錘激波傳出進氣道之后，壁面壓力整體上開始逐漸下降。在t=0.03 s時，進氣道壁面壓力呈現入口處低、出口處高的特點，并且上下壁面沿軸向壓力以近似的梯度增高。此時入口處壓力已經降至接近當地穩態時壓力。而在之后時刻，入口附近的壓力會進一步下降直至低于當地穩態時的壓力，典型的如圖中展示的t=0.08 s時刻的曲線。在該時刻，進氣道前段所受壓力低于其穩態時壓力，而進氣道后段所受的壓力仍高于穩態壓力。值得注意的是此時進氣道在靠近入口彎道處的下壁面區域。由于進氣道壁面在此處突然開始彎曲，在穩態時，該處便是一個明顯的低壓區域。但在t=0.08 s時刻，該區域的壓力進一步降低，同時其壓力梯度也更大。這會使得進氣道在該處受到較大的吸力載荷以及較大的剪切應力。

不同時刻進氣道對稱面上壓力云圖以及流線圖顯示在圖10中，圖中壓力均除以來流靜壓以進行無量綱處理。圖10(a)～圖10(d)顯示了錘激波在進氣道內的傳播過程，激波面的法向基本與進氣道中軸線方向一致。位于錘激波上游的壓力和流線未受到影響，依舊與錘激波發生前一樣，但是在錘激波下游，則可以觀察到回流的產生。值得注意的是，圖10(c)錘激波經過進氣道靠近入口的彎折處時，由于進氣道的彎曲，導致錘激波下游回流的流線向上壁面傾斜，錘激波處上壁面出現明顯的壓力集中，使得此處成為進氣道內部峰值壓力最高的部位。在錘激波傳播過程中進氣道下游產生回流，而上游氣流仍從進氣道入口流入，因而在進氣道內部堆積大量流體，形成高壓區域。圖10(d)中錘激波即將從進氣道傳出，激波面后方出現的一段高壓區域，使得流動出現分離，一部分繼續向上游流動，另一部分則流向下游，并在進氣道中部誘導產生復雜的螺旋結構。在錘激波離開進氣道后，聚集在進氣道中部的高壓區導致氣流同時向進氣道入口和出口流出。由于在進氣道出口所設定的波形持續時間較長，因而入口附近壓力下降更快，因此這一高壓區域逐漸向后移動。圖10(e)中高壓區位于進氣道中部，流動在中部分離分別向入口和出口流出，而圖10(f)由于高壓區的后移，流動分離區域也移動到了進氣道的后段。中部高壓區持續了較短時間，在圖10(f)之后不久便完全消散，此時距離錘激波的產生時間僅過了0.02 s，而此時進氣道出口的壓力還處于較高的狀態，進而導致進氣道再次出現回流，回流從進氣道入口流出，在進氣道外部產生旋渦，如圖10(g)所示。此時呈現出越靠近進氣道入口，壓力下降越快的特點。回流持續了較長的時間，并隨著進氣道出口壓力的下降而逐漸減弱。在進氣道出口壓力恢復到初始壓力時，進氣道內流動尚未恢復正常，而是直到0.195 s以后，即距錘激波發生0.185 s之后，流動恢復到初始方向并逐漸穩定，如圖10(h)所示。

圖10 不同時刻進氣道對稱面流線圖和壓力云圖Fig.10 Streamlines and pressure contours on symmetry plane of inlet at different time

圖11 不同時刻進氣道內部三維流線圖 (左：側視；右：俯視)Fig.11 3D streamlines in inlet duct at different time (left：side view; right：top view)

為了進一步分析進氣道內部的三維流動特征，圖11給出了不同時刻進氣道內部的三維流線圖，圖中每一時刻均由兩種不同視角流線圖組成。圖中流線顏色表示速度的大小，單位為m/s。t=0.01 s時的流線圖如圖11(a)所示，此時進氣道出口剛產生壓力突變，內部流動還未受到影響。在t=0.015 s時(圖11(b))，錘激波傳播至進氣道中部，可以看到錘激波下游的回流速度遠小于錘激波上游氣流的流速。從俯視圖中可以看到此時進氣道內部流動沒有出現明顯的側向運動，流線基本與進氣道中軸線方向一致。t=0.02 s時(圖11(c))，位于進氣道中心的旋渦使得流線旋轉并互相纏繞著向進氣道兩側移動。同時值得注意的是，在錘激波下游的回流中，處于進氣道中心旋渦處的氣流流速非常低(小于5 m/s)，而旋渦周邊靠近壁面的氣流流速相對較高，尤其是下壁面附近，流速為錘激波下游回流中最高。t=0.025 s時(圖11(d))，位于進氣道中部的旋渦可以在圖10(e)中觀察到其在對稱面的二維投影。而在進氣道后段的上壁面附近還可以觀察到另外兩個對稱的旋渦。t=0.03 s時(圖11(e))，氣流從高壓區同時向進氣道入口和出口流出，在進氣道內越遠離高壓區的地方流速越快。圖11(f)為t=0.08 s中部高壓區消失后出現的回流，此時回流的流速遠高于錘激波經過進氣道時其下游回流的流速，流線基本與進氣道中軸線平行，沒有出現明顯的三維流動特性。

4 進氣道換算流量的影響

進一步選用3種不同的流量條件進行錘激波過程的數值模擬。3種計算條件下穩態時的換算流量分別為30、45、60 kg/s(對應的進氣道出口馬赫數分別為Mae=0.21，0.31，0.44)。通過改變進氣道出口的反壓來達到預計的流量條件，而來流條件以及非定常計算時錘激波波形均與第3節所述相同。

為了對比換算流量變化的影響，圖12詳細列出了上下壁面各點在3種不同流量條件下的峰值壓力。可以看出，隨著換算流量(或進氣道出口馬赫數)的減小，進氣道各處所受的峰值壓力逐漸增大。

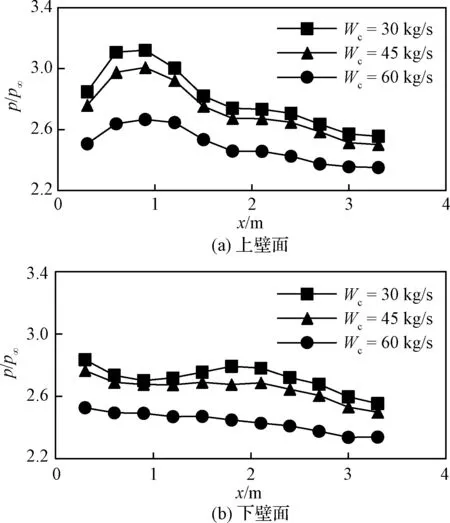
圖12 不同流量條件時上下壁面各點的峰值壓力Fig.12 Peak pressure of each point on upper and lower walls for different flow rate conditions

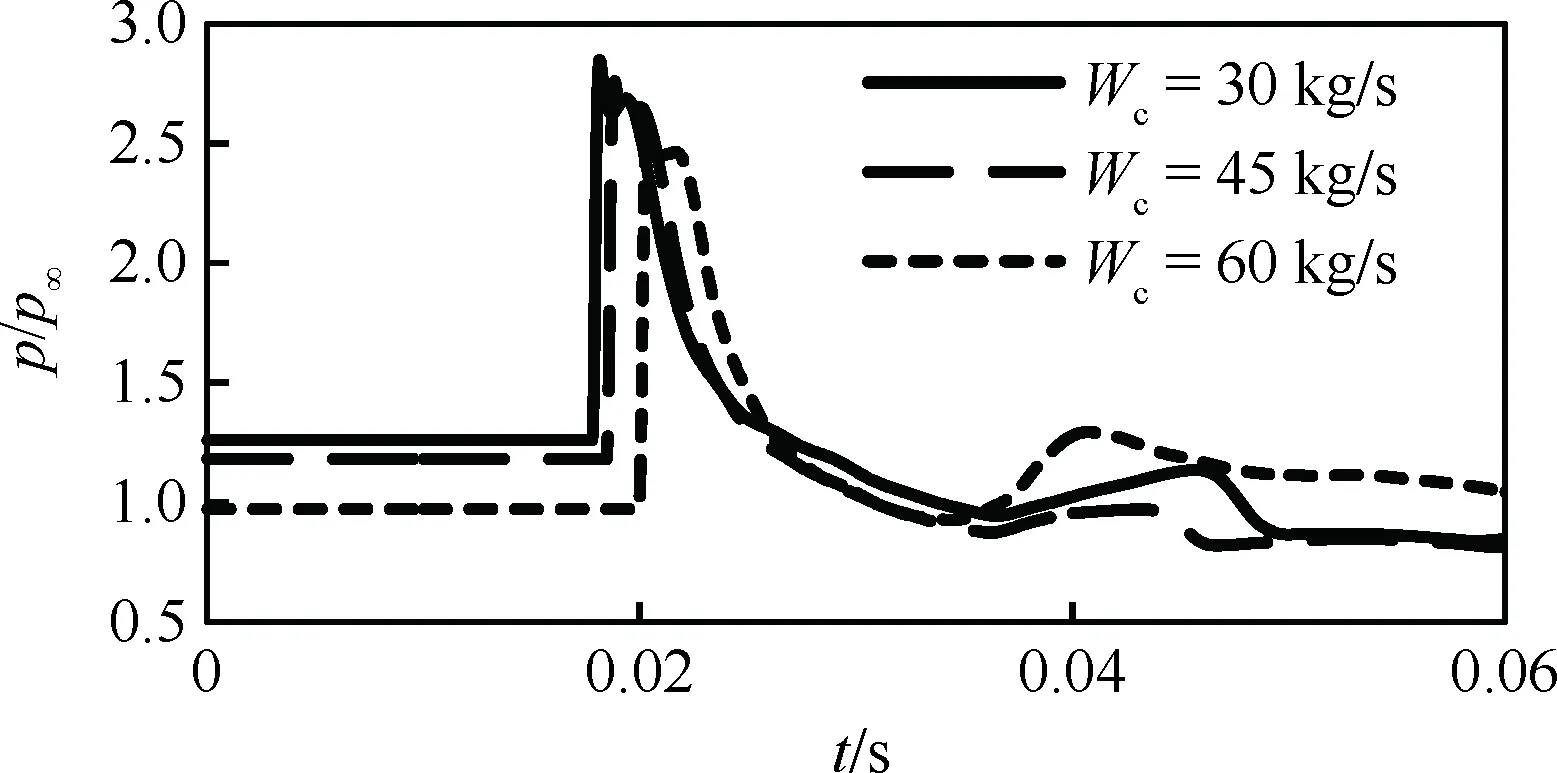
圖13 不同流量條件時點P1處壓力隨時間變化曲線Fig.13 Time history of pressure at probe point P1 for different flow rate conditions

圖13給出了點P1在3種流量條件下壓力隨時間的變化過程，其中點P1的位置已經在圖1中標出。可以看出在不同換算流量時，除了壓力的數值呈現差異，壓力開始變化的時間也有所不同，說明錘激波的傳播速度不同。依據進氣道入口附近點達到峰值的時間，在Wc=30 kg/s(出口馬赫數Mae=0.21)時，錘激波傳播速度達391 m/s(馬赫數Ma=1.15)，而在Wc=60 kg/s(出口馬赫數Mae=0.44)時，錘激波相對進氣道的平均傳播速度為306 m/s(Ma=0.9)。

5 超壓比的影響

錘激波波形的超壓比(Over Pressure Ratio, OPR)表示波形壓力變化峰值與初始壓力的比值。為分析超壓比的差異對進氣道所受壓力的影響，將錘激波波形變更為峰值壓力達3倍初始壓力，而壓力突變為峰值的時間以及壓力恢復到初始值的時間均與圖5所示的原波形相同。除了波形的改變外，計算時其他條件均保持相同。

兩種超壓比條件下上下壁面峰值壓力如圖14所示。表明增大波形的超壓比顯著增大了進氣道壁面所受的峰值壓力。超壓比由2.1增大到3使得設定的波形的峰值壓力增大了約1.43倍。而進氣道各點的峰值壓力的增大比例為1.34～1.42倍，略低于波形中峰值壓力的增大比例。

圖15給出了進氣道上壁面點P1的壓力變化曲線，可以看出在超壓比為3的條件下，點P1達到峰值的時間更早，說明錘激波在進氣道內傳播速度更快。在超壓比為3時，錘激波在進氣道內傳播的平均速度為379 m/s(Ma=1.11)。

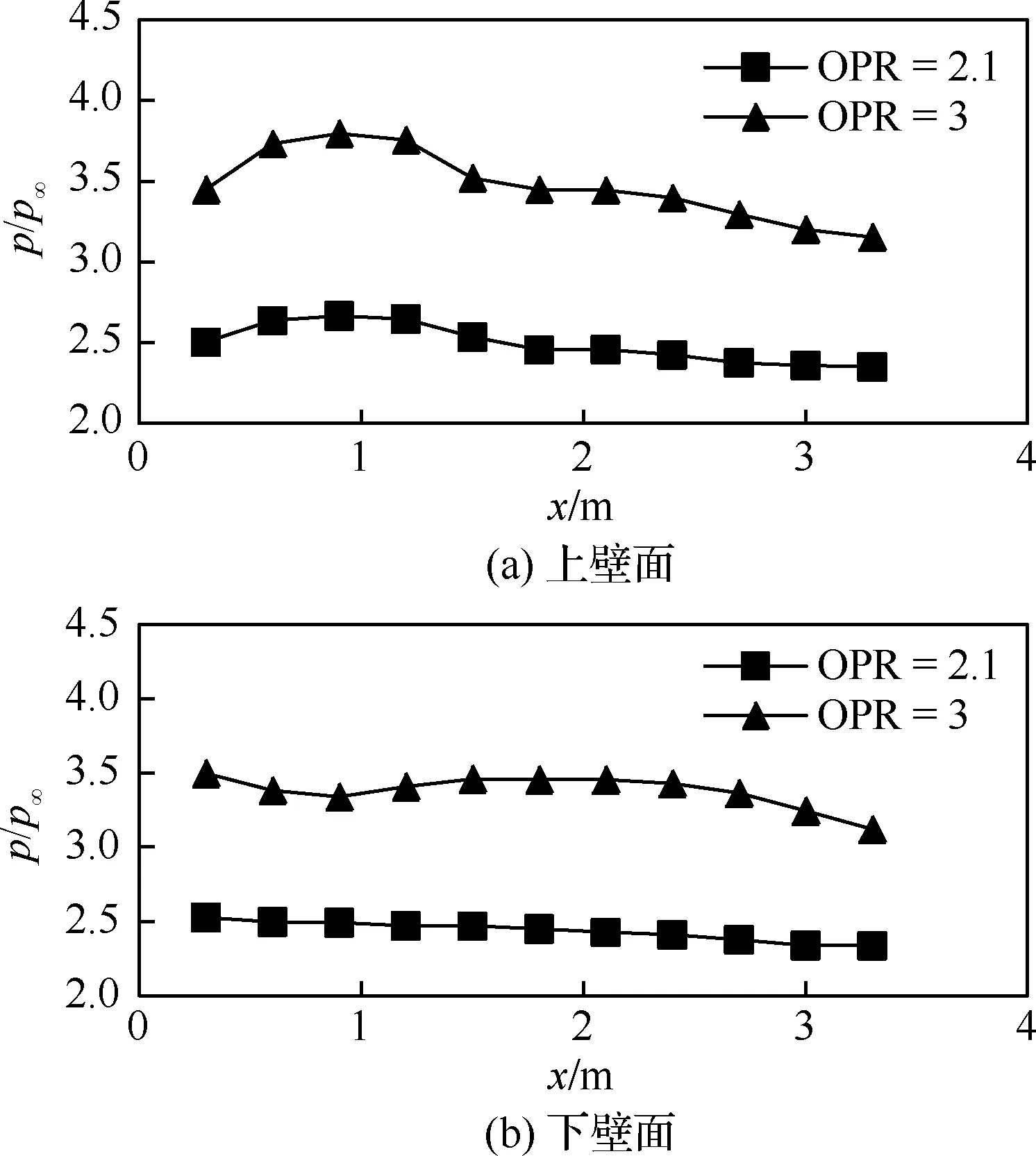
圖14 不同超壓比時上下壁面各點的峰值壓力Fig.14 Peak pressure of each point on upper and lower walls for different Over Pressure Ratios(OPRs)

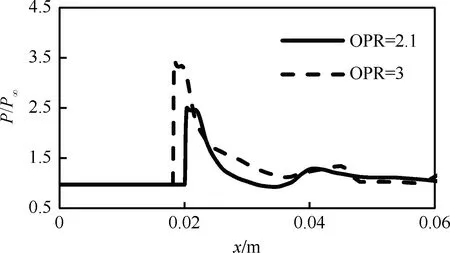
圖15 不同超壓比時點P1處壓力隨時間變化曲線Fig.15 Time history of pressure at probe point P1 for different over pressure ratios

6 中心線幾何形狀的影響

進氣道的幾何形狀會對錘激波壓力的分布情況產生影響。對于S形進氣道幾何造型方面的研究較多，其中Lee和Boedicker[19]提出的關于中心線形狀的3種曲線方程得到了非常廣泛的應用。本文選取其中兩條曲線與原曲線進行對比，探討其錘激波壓力分布的差異。3條曲線如圖16所示，曲線1為原M2129型進氣道中心線，曲線2和3來自文獻[19]，圖中橫縱軸分別表示中心線各點x坐標和z坐標與對應方向總長度的比值。對于前半段(Δx<0.5)，相比于曲線1，曲線2初始時曲率較小，方向變化緩慢，之后曲率迅速增大，而曲線3則一開始曲率最大，方向變化最快，之后變得最為平緩。在后半段(Δx>0.5)，曲線2和3變化規律相反。計算時除了中心線形狀外，其他參數的設定完全相同。

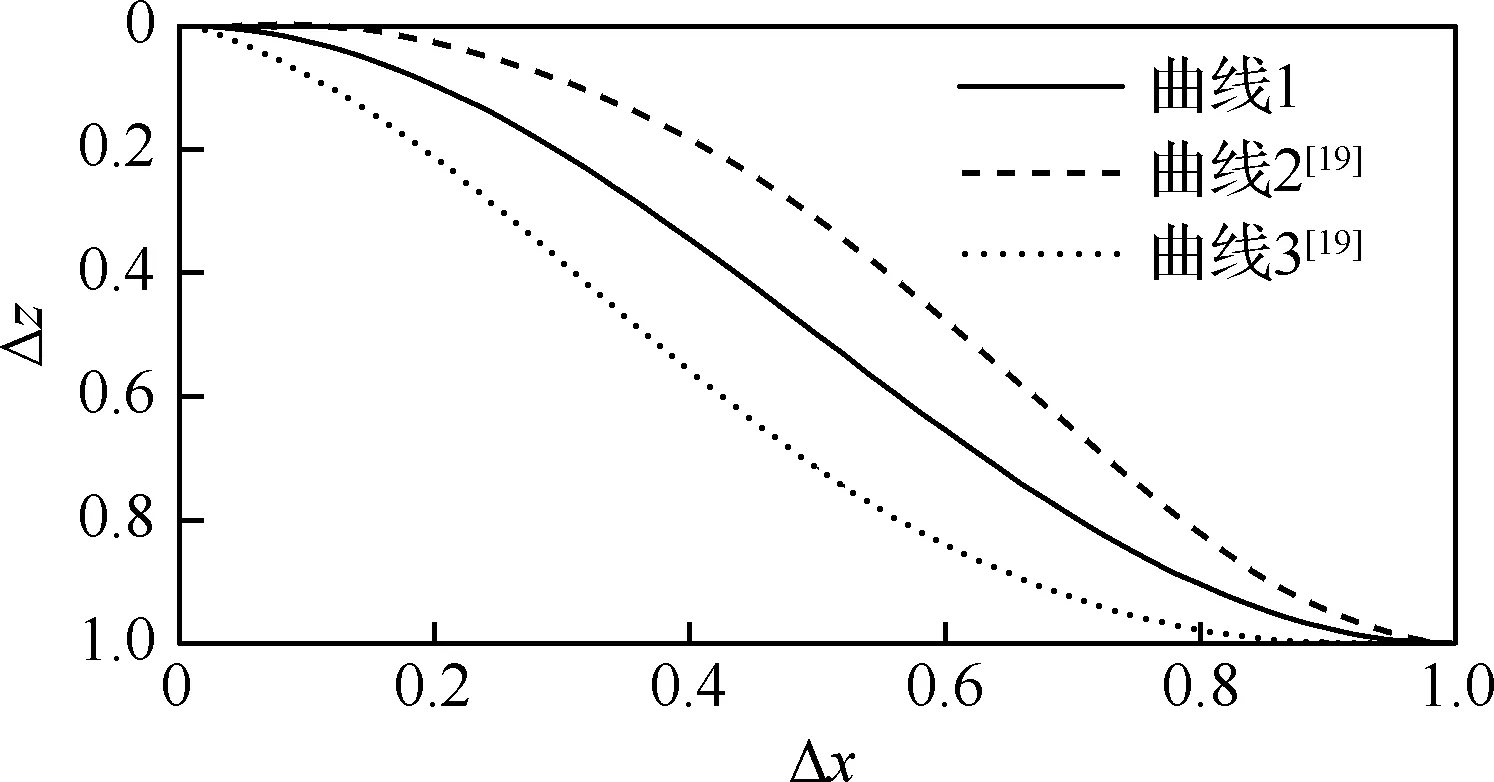
圖16 進氣道中心線幾何形狀Fig.16 Geometry shape of inlet centerlines

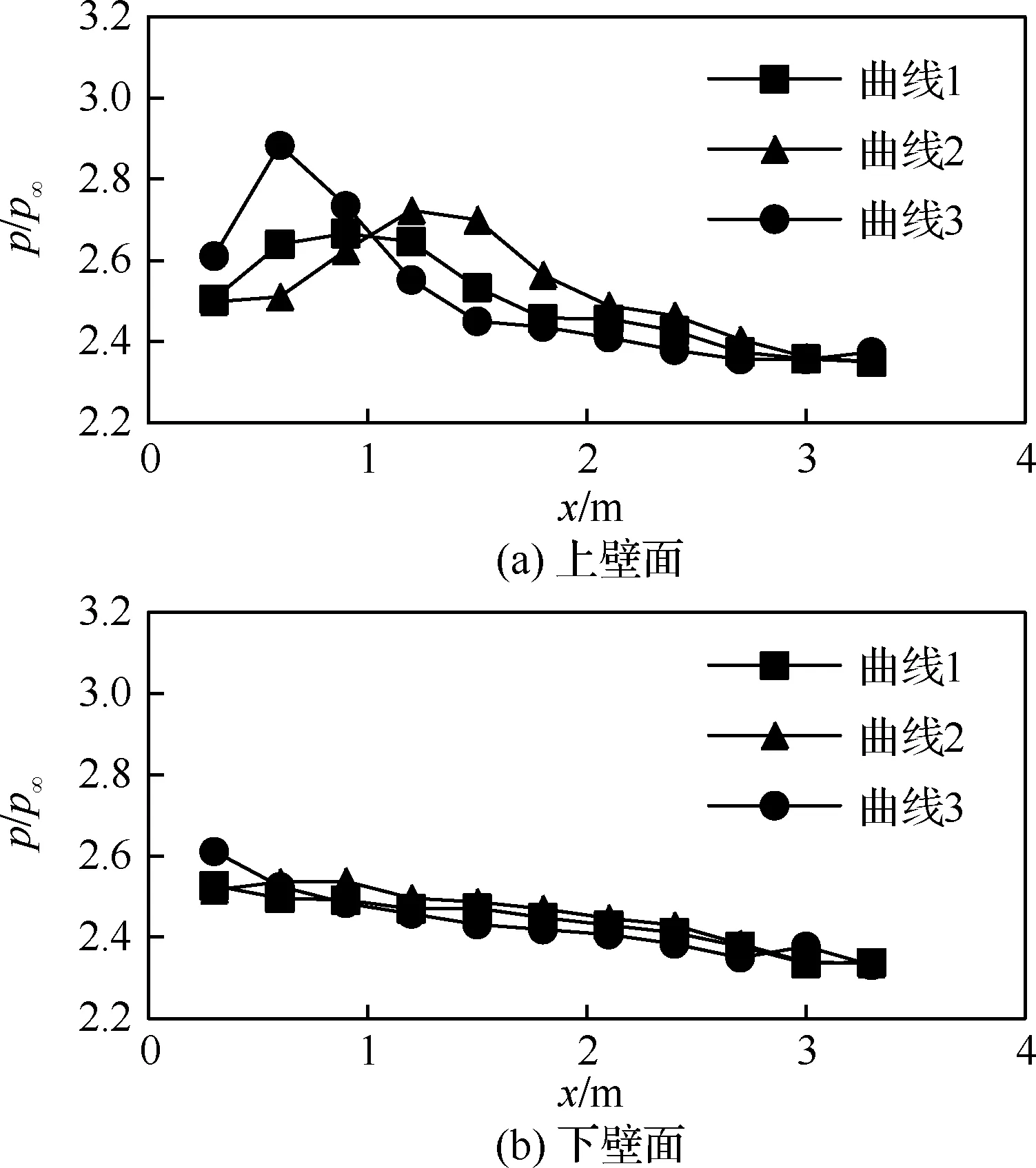
圖17 不同中心線時上下壁面各點的峰值壓力Fig.17 Peak pressure of each point on upper and lower walls with different centerlines

圖17給出了3種不同中心線形狀的進氣道上下壁面各點在錘激波演化過程中的峰值壓力。對比可以看到峰值壓力的變化在進氣道前半段的上壁面最為明顯，最大峰值壓力的位置和大小均有所不同。曲線2開始最平緩之后曲率迅速變大，相應的進氣道靠近入口位置峰值壓力較小，最大峰值所處位置更靠后。曲線3開始曲率很大，之后平緩，相應的進氣道模型受到最大峰值壓力的地方更靠前。而進氣道后半段各點的峰值壓力受幾何形狀的影響較小。通過對比可以看出進氣道中心線形狀的變化對其錘激波壓力分布具有重要的影響。但是峰值壓力還受到其他因素的影響，如所處進氣道的位置、進氣道截面積變化等。因而各處峰值壓力的變化并不與曲率分布完全對應。

7 結 論

本文選取M2129型S形進氣道模型進行了錘激波動態過程的數值模擬。利用在進氣道出口設定壓力波形的方法模擬喘振時發動機的壓力變化。詳細分析了來流馬赫數為0.65，進氣道初始換算流量為60 kg/s的條件下錘激波經過進氣道時壁面的壓力變化和內部的三維流動情況。并進一步分析了不同換算流量、超壓比和進氣道中心線幾何形狀對進氣道所受錘激波壓力的影響。結果表明：

1) 在馬赫數為0.65，進氣道初始換算流量為60 kg/s(出口馬赫數Mae=0.44)的條件下，錘激波以相對進氣道大約306 m/s(Ma=0.9)的速度向上游傳播，相對激波上游來流的速度約481 m/s(Ma=1.42)。在錘激波傳播過程中伴隨三維復雜流動結構和回流的產生。通過記錄進氣道上下壁面各點的壓力隨時間變化情況，發現進氣道上下壁面所受峰值動態壓力達到了來流靜壓的2.3～2.65倍。錘激波經過進氣道彎道處時，彎道外側的壁面壓力會大于內側，尤其靠近入口的彎折處，上壁面所受的峰值壓力為整個進氣道所受錘激波壓力最高的部位。在錘激波傳出進氣道后，進氣道內部流動不會立刻恢復到初始流動，而是經歷了由進氣道中部同時向入口和出口流出以及隨后變為完全回流等流動狀態，經過了大約0.185 s后才恢復為正常狀態。

2) 通過對不同換算流量條件下錘激波演化過程的對比，發現較低流量時進氣道所受峰值壓力更大，錘激波相對進氣道傳播速度更快。對比不同超壓比時錘激波演化過程，發現較高超壓比時進氣道受到峰值壓力更大，錘激波傳播速度更快。

3) 對具有不同中心線幾何形狀的進氣道進行錘激波計算，表明了中心線形狀對錘激波壓力的大小和分布有重要影響。不同中心線形狀時，S形進氣道前半段的彎道所受的錘激波壓力產生了明顯的改變，曲率較大的地方易產生大的錘激波峰值壓力，而后半段受到的影響較小。

[1] YOUNG L C, BEAULIEU W D. Review of hammershock pressures in aircraft inlets[J]. Journal of Aircraft, 1975, 12(4): 210-216.

[2] MARSHALL F L. Prediction of inlet duct overpressures resulting from engine surge[J]. Journal of Aircraft, 1973, 10(5): 274-278.

[3] KURKOV A P, SOEDER R H, MOSS J E. Investigation of the stall hammershock at the engine inlet[J]. Journal of Aircraft, 1975, 12(4): 198-204.

[4] BELLMAN D, HUGHES D. The flight investigation of pressure phenomena in the air intake of an F-111A airplane: AIAA-1969-0488[R]. Reston, VA: AIAA, 1969.

[5] NUGENT J, HOLZMAN J K. Flight-measured inlet pressure transients accompanying engine compressor surges on the F-111A airplane: NASA TN D-7696[R]. Washington, D.C.: NASA, 1974.

[6] EVANS P J, TRUAX P. YF-16 air induction system design loads associated with engine surge[J]. Journal of Aircraft, 1975, 12(4):205-209.

[7] HINDASH I, BUSH R, COSNER R. Computational modeling of inlet hammershock wave generation: AIAA-1990-2005[R]. Reston, VA: AIAA, 1990.

[8] PAYNTER G, MAYER D, TJONNELAND E. Flow stability issues in supersonic inlet flow analyses: AIAA-1993-0290[R]. Reston, VA: AIAA, 1993.

[9] GOBLE B D, KING S, TERRY J, et al. Inlet hammershock analysis using a 3-D unsteady Euler/Navier-Stokes code: AIAA-1996-2547[R]. Reston, VA: AIAA, 1996.

[10] YTTERSTRCM A, AXELSON E. Hammershock calculations in the air intake of JAS 39 GFUPEN using dual timestepping: AIAA-1999-3113[R]. Reston, VA: AIAA, 1999.

[11] BECKER J. Dynamic hammershock effects on the air intake design of supersonic aircraft[M]∥Structures under Shock and Impact Ⅲ. Southampton: WIT Press, 1994: 419-426.

[12] HSIEH T, WARDLAW A B, COLLINS P, et al. Numerical investigation of unsteady inlet flowfields[J]. AIAA Journal, 1987, 25(1): 75-81.

[13] GRIDLEY M, SYLVESTER T, TRUAX P. Impact of a probabilistic approach on inlet hammershock design loads: AIAA-1999-2114[R]. Reston, VA: AIAA, 1999.

[14] 朱宇, 沈天榮. 飛機進氣道錘擊波載荷評估方法研究[J]. 航空發動機, 2015， 41(3): 6-11.

ZHU Y, SHEN T R. Evaluation approach of hammer shock loading for aircraft inlet[J]. Aeroengine, 2015, 41(3): 6-11 (in Chinese).

[15] ANDERSON B H, REDDY D R, KAPOOR K. Study on computing separating flows within a diffusion inlet S-duct[J]. Journal of Propulsion & Power, 1994, 10(5): 661-667.

[16] NICHOLS R. Calculation of the flow in a circular S-duct inlet: AIAA-1991-0174 [R]. Reston, VA: AIAA, 1991.

[17] STANLEY R, MOHLER J. Wind-US flow calculations for the M2129 S-duct using structured and unstructured grids: AIAA-2004-0525[R]. Reston, VA: AIAA, 2004.

[18] DEBIASI M, HERBERG M R, YAN Z, et al. Control of flow separation in S-ducts via flow injection and suction: AIAA-2008-0074[R]. Reston, VA: AIAA, 2008.

[19] LEE C, BOEDICKER C. Subsonic diffuser design and performance for advanced fighter aircraft: AIAA-1985-3073[R]. Reston, VA: AIAA, 1985.