基于FQFD的太陽能無人機設計指標排序方法

周偉，李賽，王學仁，謝飛

1. 火箭軍工程大學 動力工程系，西安 710025 2. 西北工業大學 航天學院 航天飛行動力學技術重點實驗室，西安 710072

太陽能無人機是依靠太陽輻射能作為全部能源來源的飛行器。太陽能無人機利用高空近乎無窮無盡的太陽輻射能作為飛行的動力并儲存白天采集的能量以供夜間飛行，因此具有在高空(10～30 km)持續數年的駐留飛行能力。由于其可以不用消耗“能源”，不用反復起降維護，能在高空持久飛行，可用于通信(中繼)、偵察、監視、氣象環境監測等，是常規衛星、常規動力高空長航時無人機、高空飛艇等作為空中載荷平臺的重要補充。許多國家的學者與航空工業部門都在進行相關技術的研究。

目前對太陽能飛機的設計研究主要集中在總體設計方法、分系統技術指標、高效氣動布局和大展弦比輕質結構等方面[1]，著重于提高飛機的飛行性能，而對方案設計中技術指標的系統關聯性、重要性研究則鮮有報道。太陽能飛機氣動特性、太陽能電池功率面密度、二次電池能重比、推進系統功重比及效率、結構重量系數、白天爬升與夜間下滑的高度等總體設計中的參量密切關聯，影響著太陽能無人機的總體性能[2]。進行太陽能無人機總體設計指標重要度排序研究，可提高太陽能無人機設計與需求的針對性和有效性，對其總體設計來說具有重要意義，但目前還沒有有效的排序分析方法。

利用系統工程的方法(如質量功能展開(QFD)、TRIZ、田口法等)開展無人機技術指標評價排序成為當前一個新的研究熱點。QFD[3]是一種將用戶需求轉化為產品工程技術性能的多層次系統演繹、分析方法。傳統的QFD采用“質量屋”[4](House of Quality，HoQ)二元矩陣展開框架，能最大限度地滿足用戶需求。

Tan[5]研究指出QFD方法作為一個系統集成工具，可用于低速長航時無人機的概念設計配置階段，提出了一個四級標準QFD模型來確定優先影響客戶選擇的重要設計變量，并將客戶屬性部署到性能參數中。解建喜等[6]基于QFD方法提出了飛機頂層決策設計的遞階層次結構，引入競爭性因子建立了評判模型，提出遞階質量屋結構并將之應用于飛機頂層設計中；陳毅雨等[7]采用基于灰關聯分析的質量功能展開(GQFD)方法對警用反恐無人機的任務需求進行了分析，建立HoQ分析模型，得到了警用反恐無人機的關鍵技術性能及其重要度排序。趙雷[8]通過QFD工具逐層分解客戶需求、定位功能和物理參數，分析功能的重要性；通過模糊數學中的最大隸屬度模糊評價原理，分析多種方案的適應性，得出定量分析結果，避免以往依靠經驗和類比的不確定性。張付英等[9]提出了集成模糊聚類法和模糊擴展層次分析法的用戶需求分析方法，將模糊的、不確定性用戶需求信息進行準確化和定量化處理，為產品規劃質量屋的構建和質量功能的瀑布式展開提供有效的用戶需求分析手段。

由于QFD研究方法具有對象、任務針對性強，分析過程獨立性高的特性。因此，上述文獻提出的方法雖能夠較好地解決其自身提出的問題，但并不能完全移植用于太陽能無人機的總體設計指標排序研究工作中。

本文針對太陽能無人機任務針對性強、約束條件苛刻、系統復雜度高、設計自由度小等特點，在傳統QFD評價方法的基礎上，考慮任務需求表達時的主觀性和模糊性，提出了基于模糊質量功能展開(FQFD)的太陽能無人機總體設計指標排序方法。采用模糊數更加準確地刻畫用戶的語言模糊和技術指標間的不確定性，不僅具有把定性分析轉換成定量分析等優點，而且能有效減少人為因素帶來的干擾[10]。在計算太陽能無人機技術指標重要度時，由于技術特性的隸屬度函數未知，提出采用α加權的平均截集去模糊化方法，有效解決了多指標三角模糊數聚集比較、排序困難的問題。依據去模糊重要度的大小對太陽能無人機技術指標進行綜合衡量和評價，為后續優化設計決策提供參考依據。

1 QFD方法簡介

QFD方法是一種將用戶需求轉化為產品工程技術性能的分析方法。該方法最早由日本科學家赤尾洋二教授[11]提出，并由邵家俊[12]、熊偉和權婧雅[13]引入中國，隨后在眾多領域展開廣泛研究探索。1987年，美軍在《可靠性和維修性2000大綱》中把QFD列為減少質量波動、提高產品可靠性的重要方法之一[14]。

準確理解用戶的需求是QFD方法的關鍵，其核心是質量屋，給以合適的輸入信息，通過建立一系列的矩陣將顧客需求、技術指標等定性要素以定量的方式計算表征，獲得更為科學的結論。圖1為質量屋模型，共由7部分組成，如圖1所示。

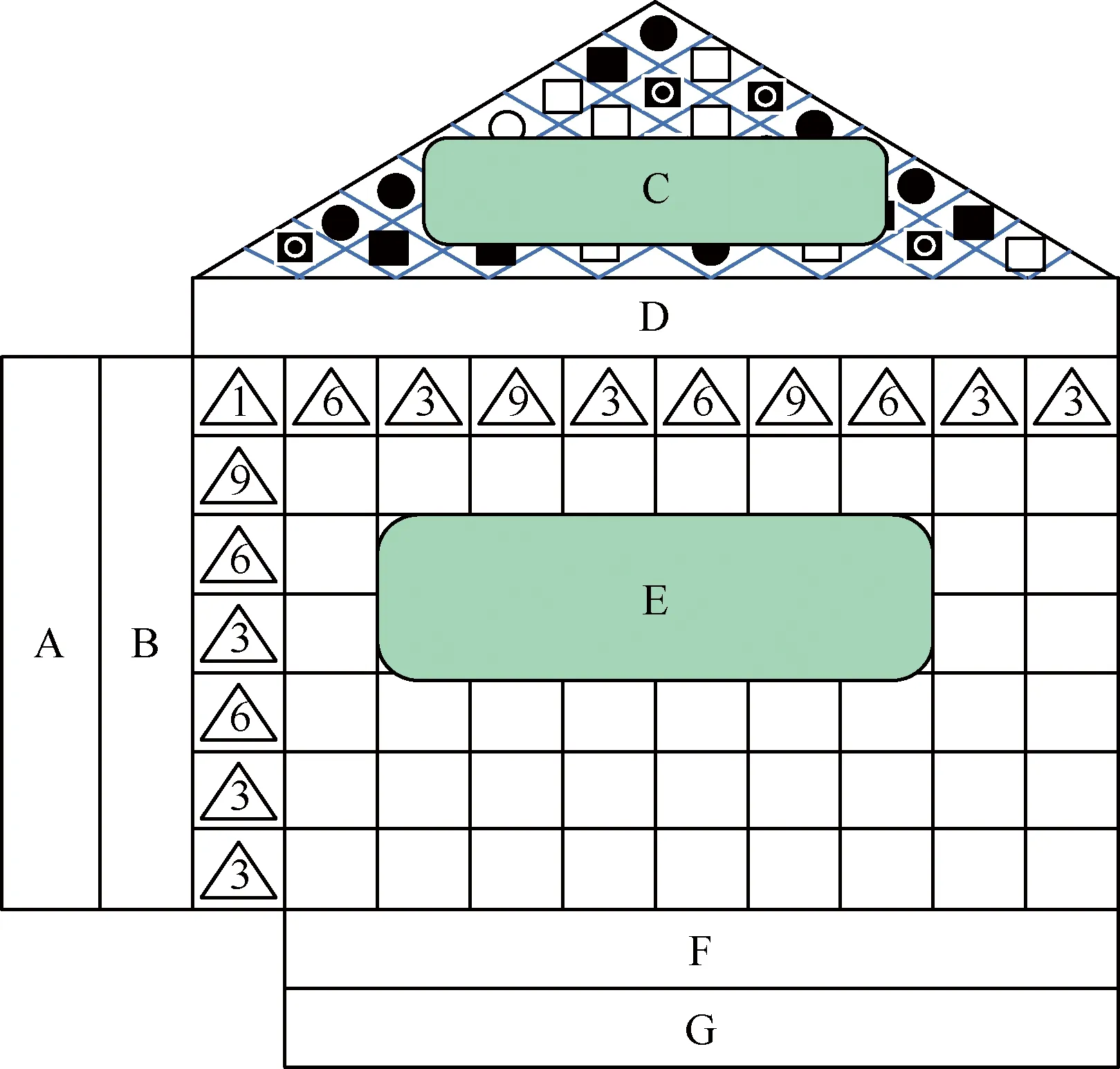
注：左墻A—顧客的需求；左墻B—需求重要度矩陣；屋頂C—技術特性的自相關矩陣；天花板D—技術特性；房間E—技術特性與相對應的顧客需求之間的相互關系矩陣；地板F—技術特性重要度矩陣；地下室G—技術特性排序。圖1 質量屋模型Fig.1 House of quality model

2 模糊數基礎

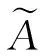
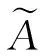
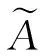
其α-截集定義為

α∈[0,1]。

有關模糊數的算術運算規則可參考文獻[17-18]，本文采用實數運算符號。

3 FQFD綜合評價方法

3.1 評價方法

FQFD方法是指將模糊理論和常規QFD方法相結合,基于常規QFD方法的質量屋框架,利用模糊理論彌補常規QFD方法不能有效地處理系統設計中主觀、定性和模糊信息的不足所形成的方法[6]。其核心是模糊質量屋(FHoQ)模型的建立和完成過程，方法的具體評價分為以下4個步驟：

步驟1確定任務需求的模糊表達式

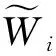
步驟2構建技術指標矩陣

天花板D表示技術指標ECi，通常由可實現的具體參數表示；屋頂C是技術指標自相關矩陣Dsj，表示技術指標之間的相關性，它能明確技術指標之間是怎樣相互作用或者互不影響的，由評價專家給出相關性判斷，或由性能仿真、敏感性計算分析得出。

步驟3構建模糊相關性矩陣

步驟4重要度評價

地板F是技術指標重要度，由于相關性矩陣采用三角模糊數，因此需要去模糊化后才能表征對比，為解決三角模糊數集比較、排序困難的問題，本文采用α加權的平均截集去模糊化方法(見3.4節中的式(9))計算獲得各技術指標的綜合評價指標；地下室G是重要度排序，依據綜合評價獲得技術指標排序。

3.2 數學模型

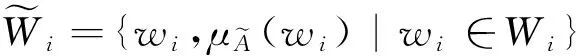
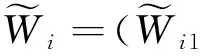
i=1, 2, …,m；k=1, 2, …,r

(1)

式中：⊕為模糊數的加法運算符。

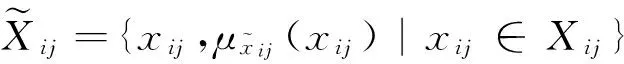
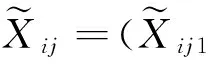
i=1, 2, …,m;j=1, 2, …,n;k=1, 2,…,r

(2)

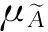
(3)

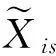
(4)

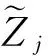
3.3 α-截集模糊加權平均

(5)

(6)

式中：i=1,2,…,m；j=1,2,…,n。

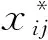
(7)

(8)

式中：i=1, 2, …,m；j=1, 2, …,n；t,qi≥0。

3.4 去模糊化排序

去模糊化就是將模糊數轉換成一個明確的數值，去模糊化并沒有固定的步驟，而去模糊化的方法有很多，較常用的去模糊化的方法有：重心法、最大歸屬度平均法、高度法[22]等。文獻[23]提出的基于“面積”度量的模糊數排序方法與上述3種方法類似，它們都要求已知確切的隸屬度函數。若隸屬度函數未知，則這些方法無法使用。這里又考慮到α值表示了獲取信息的可能性水平和不確定度，α值越大，可能性越大，不確定程度則越低。為有效刻畫用戶語言模糊和技術指標間的不確定性，采用如下α加權修正的平均水平截集去模糊化方法，通過使用該方法能有效解決多指標三角模糊數聚集導致排序困難的問題。計算公式為

j=1, 2, …,n

(9)

式中：α1,α2, …,αN為不同的α-截集水平，且α1<α2<…<αN=1。

根據式(9)可計算各技術特性的不同α-截集對應的去模糊數值，繼而根據模糊值的大小對技術特性進行綜合評價和排序，為產品提高質量、改進性能、合理規劃提供科學依據。

4 實例研究

本節利用FQFD方法對太陽能無人機的技術指標進行綜合排序研究，驗證分析方法的合理性與可行性。

從無人機研究所、潛在用戶方和重點高校相關專業資深研究人員中隨機選擇2位專家，組成6人行業QFD評價組。評價組確定了4項任務需求(用CRi表示)、10項工程特性(用XCi表示)、14項技術指標(用ECi表示)，如表1所示。

由任務需求到技術指標，是從定性到定量，從模糊到精確，從任務需求的語言性描述到太陽能無人機具體技術指標的確定，為實現裝備設計、生產奠定基礎。所以，QFD的本質是一種需求轉化方法，以任務需求為輸入，經層層映射，得到技術指標需求輸出，其過程如圖2所示。

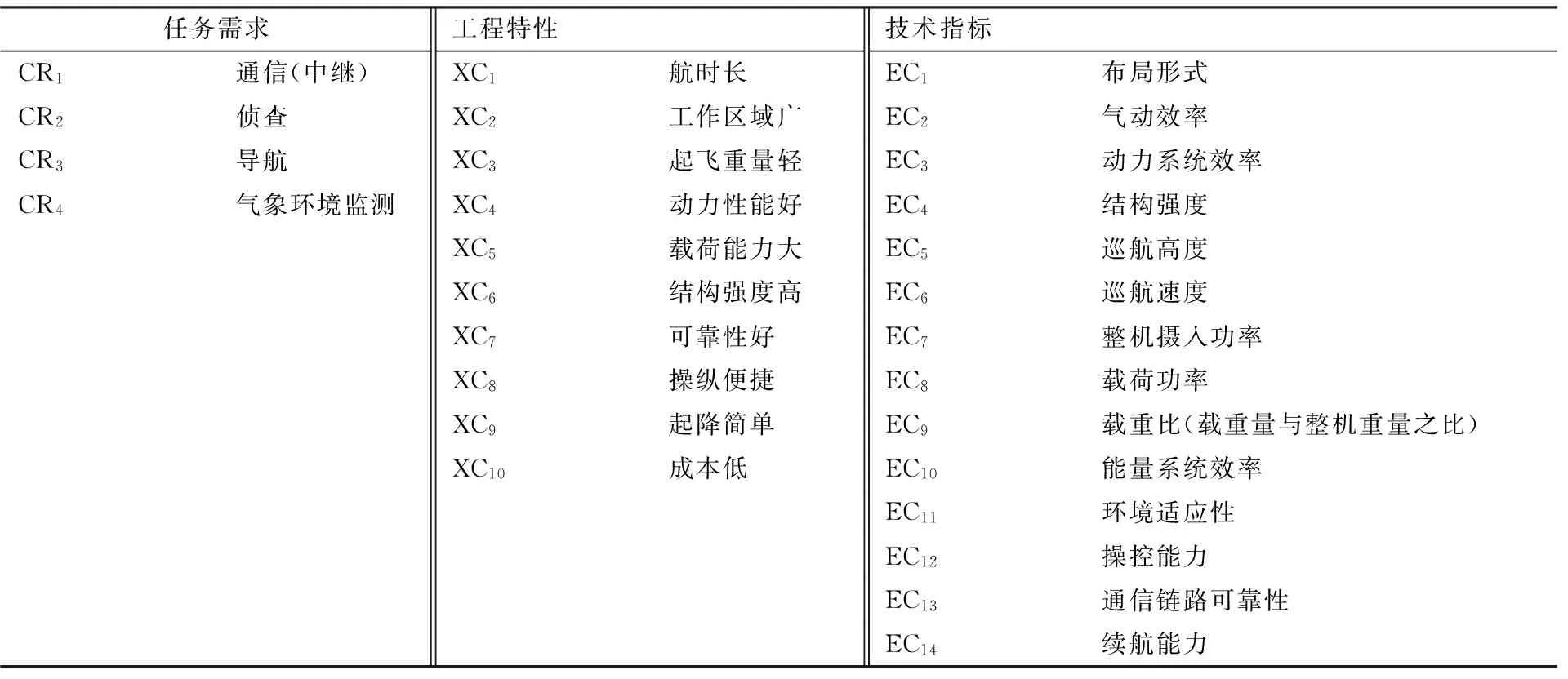
表1 太陽能無人機任務需求與技術指標Table 1 Task demands and technical specifications of solar powered UAV

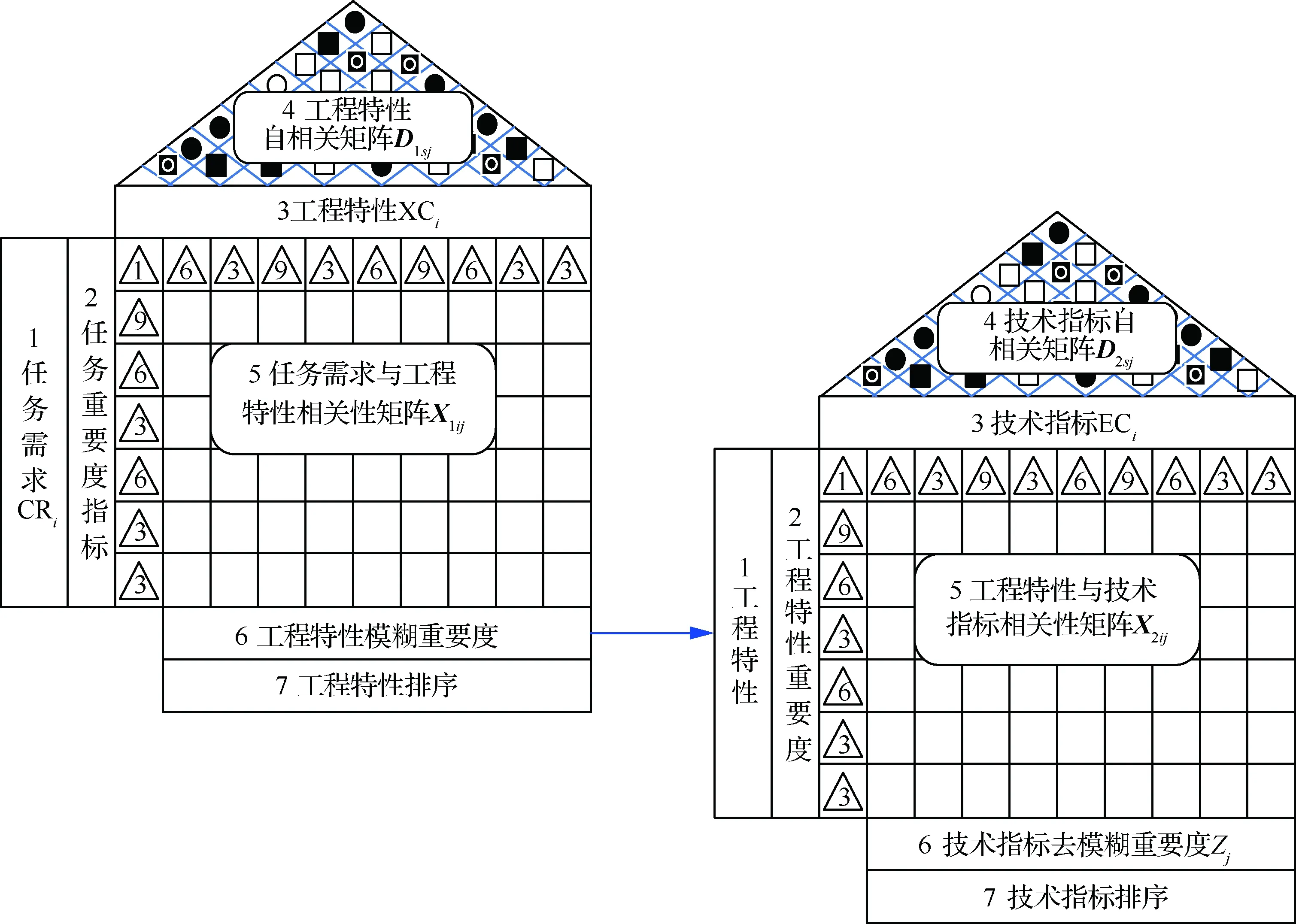
圖2 需求映射過程Fig.2 Demand mapping process

根據FQFD方法，首先確定任務需求權重，任務需求通常采用語言變量來描述需求的重要度，具有模糊性和不確定性，本文采用三角模糊數來表達，并通過模糊加權平均得到任務需求模糊權重。假設任務需求重要度由“不重要”、“較不重要”、“重要”、“較重要”、“非常重要”5個等級語言變量來描述，其對應的三角模糊數可表示為(0, 0.1, 0.3)、(0.2, 0.3, 0.5)、(0.4, 0.5, 0.7)、(0.6, 0.7, 0.9)、(0.8, 0.9, 1.0)。任務需求與技術特性之間的相關度用“0=極弱相關”、“1=弱相關”、“3=相關”、“5=強相關”4個等級的語言變量來描述，其對應三角模糊數分別為(0, 0.15, 0.30)、(0.25, 0.40, 0.55)、(0.50, 0.65, 0.80)、(0.75, 0.90, 1.00)。

根據式(1)，計算6位專家對4項任務需求重要度的評估，即計算任務需求的三角模糊權重，計算結果如表2所示。

由QFD專家評價組給出工程特性的自相關對稱矩陣D1sj，根據式(2)和式(3)得到真實任務需求和工程特性之間的相關模糊度量，如表3所示。

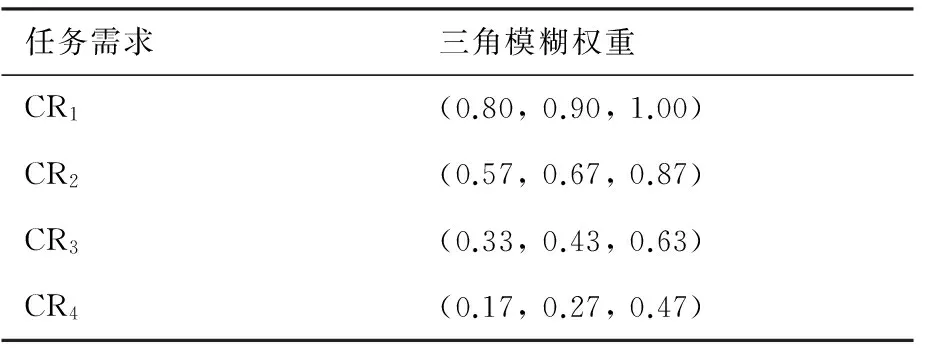
表2 任務需求的三角模糊權重Table 2 Triangular fuzzy weight of task demand

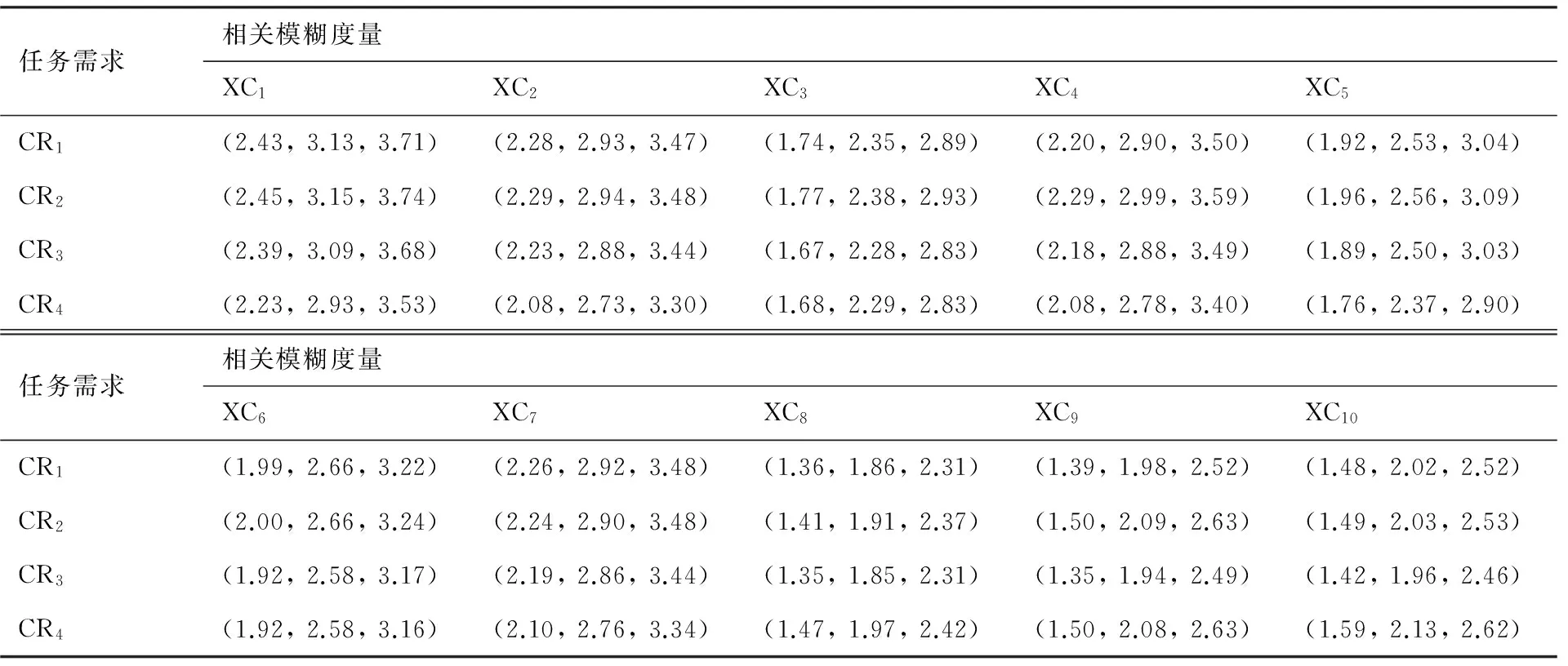
表3 考慮自相關矩陣任務需求和工程特性之間的相關模糊度量Table 3 Related fuzzy measures between task demand and engineering characteristics considering autocorrelation matrix

根據式(4)，計算工程特性的三角模糊重要度，結果如表4所示。

由QFD專家評價組給出技術指標的自相關對稱矩陣D2sj，根據式(2)和式(3)得到真實的工程特性與技術指標之間的相關模糊度量，結果如表5所示。應用式(7)和式(8)計算技術指標重要度的α-截集的上下限，結果如表6所示。

根據式(9)采用α加權修正的平均水平截集去模糊化方法，計算每一個技術指標的去模糊值，根據其值進行排序，結果如表7所示。

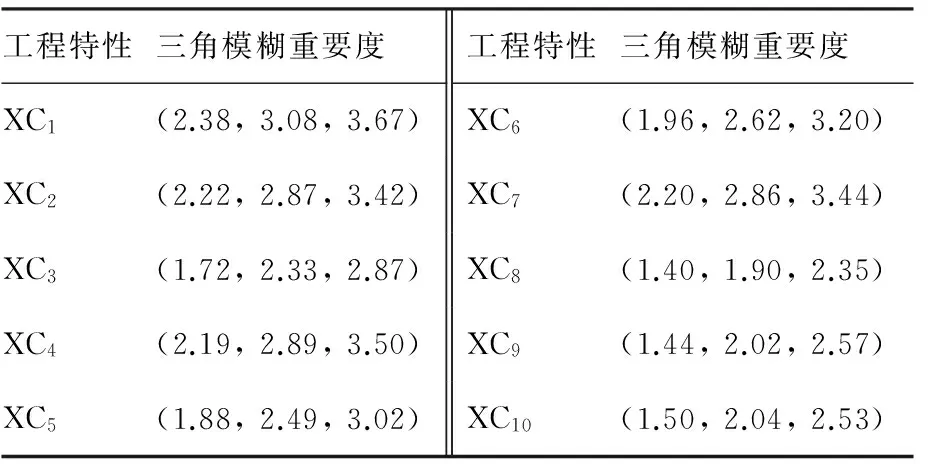
表4 工程特性的三角模糊重要度

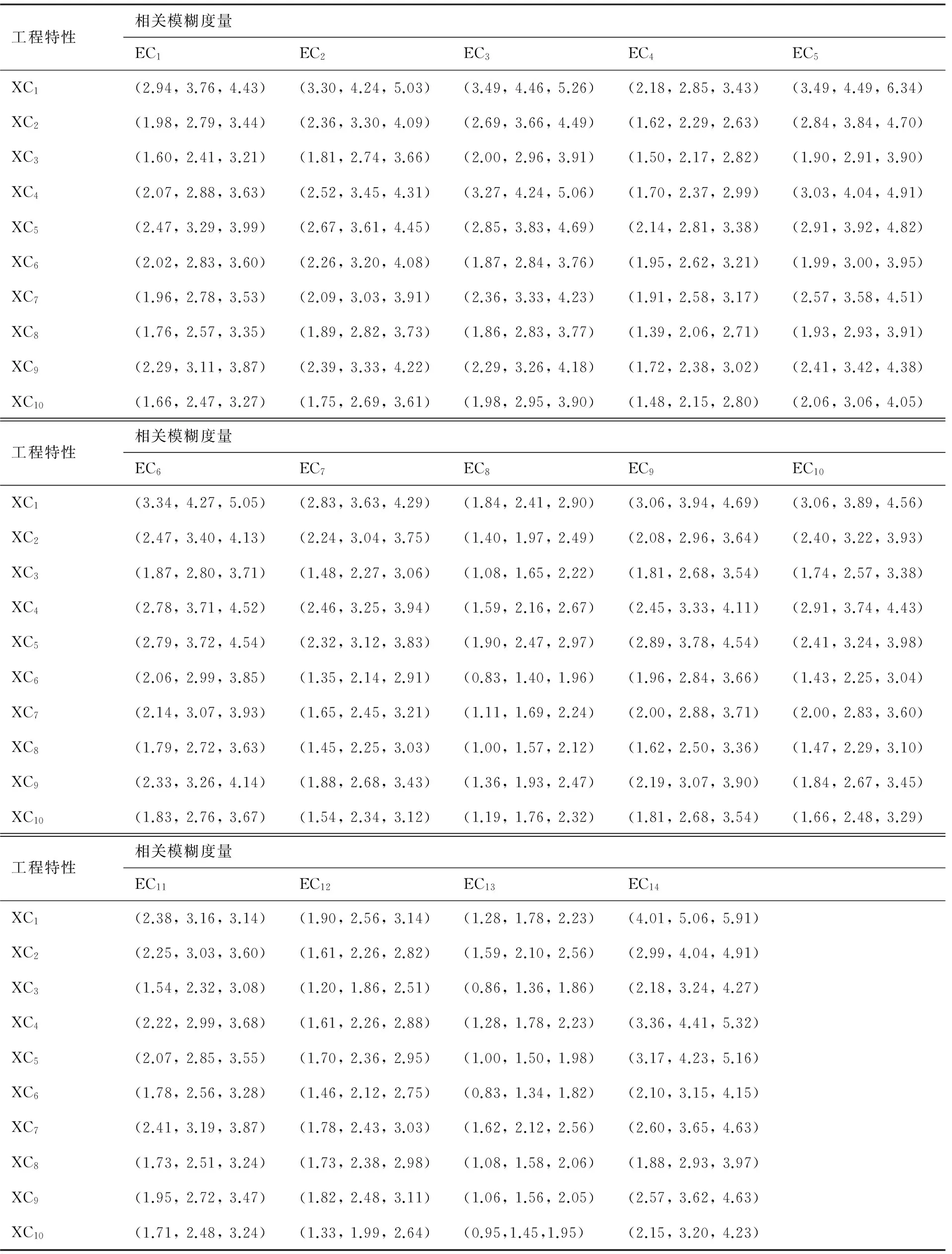
表5 工程特性和技術指標之間的相關模糊度量Table 5 Related fuzzy measures between engineering characteristics and technical specifications

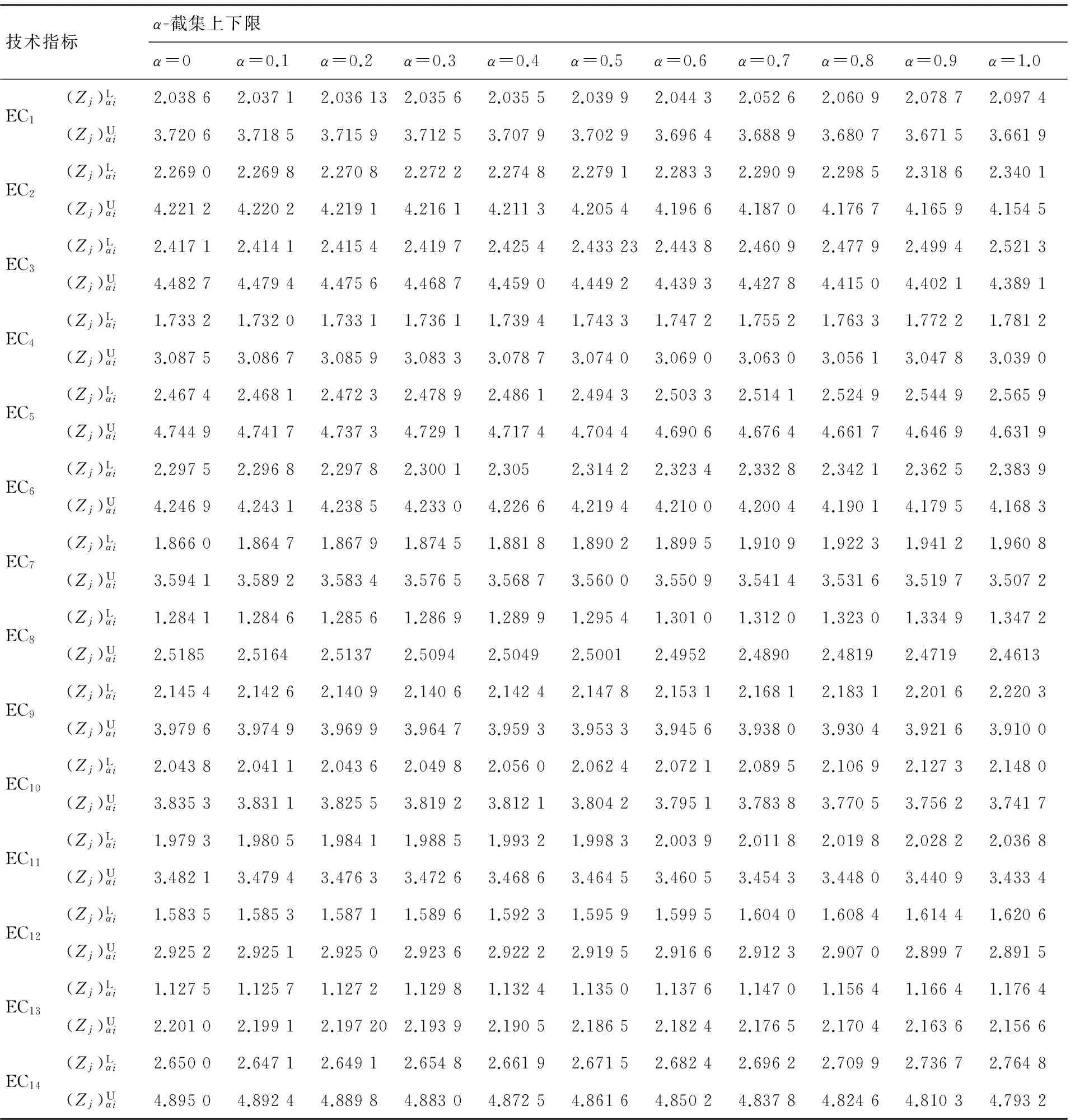
表6 技術指標重要度的α-截集的上下限Table 6 Upper and lower limits of α -cut set based on importance of technical specifications

表7 太陽能無人機技術指標重要度排序Table 7 Importance-sorting of technical specifications of solar powered UAV

通過工程特性的定量計算分析可知，航時長、動力性能好、工作區域廣這3項工程特性對太陽能無人機任務需求具有十分重要的影響。因此，在長航時太陽能無人機總體設計時，應給予其充分重視。由排序表7可知，對于太陽能無人機來說，續航能力、巡航高度、動力系統效率、巡航速度、氣動效率5項指標分別排列重要度前5位，在總體方案設計過程中應將其設為核心技術指標[24]，進行優化設計。

5 結 論

1) 本文提出的基于FQFD的太陽能無人機設計指標排序方法，可將模糊的任務需求轉化為定量數值分析，計算出技術指標重要度排序，為總體設計提供科學依據。

2) 續航能力、巡航高度、動力系統效率、巡航速度、氣動效率5項指標是長航時太陽能無人機最重要的技術性能，在總體方案設計和系統優化設計過程中應將其設為核心技術指標，著重進行分析研究。

3) 對于長航時太陽能無人機，航時長、動力性能好、工作區域廣這3項指標，是完成通信、偵查、導航等任務的重要工程特性。

4) 本文提出的綜合評價方法，對于專家的打分具有一定的依賴性。增大專家抽取數質量或采用相關學科模擬仿真結果取代專家模糊評分，能一定程度上提高排序的準確性，增強評估結果的客觀性，但同時會增大工作量、加大計算復雜度，在應用時應視情確定。

[1] 馬東立, 包文卓, 喬宇航. 基于重力儲能的太陽能飛機飛行軌跡研究[J]. 航空學報, 2014, 35(2): 408-416.

MA D L, BAO W Z, QIAO Y H. Study of flight path for solar-powered aircraft based on gravity energy reservation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 408-416 (in Chinese).

[2] 昌敏, 周洲, 鄭志成. 太陽能飛機原理及總體參數敏度分析[J]. 西北工業大學學報, 2010, 28(5): 792-796.

CHANG M, ZHOU Z, ZHENG Z C. Flight principles of solar-powered airplane and sensitivity analysis of its conceptual parameters[J]. Journal of Northwestern Polytechnical University, 2010, 28(5): 792-796 (in Chinese).

[3] SUN J， KALENCHUK D K， XUE D， et al. Design candidate identification using neural network-based fuzzy reasoning[J]. Robotics and Computer Integrated Manufacturing, 2000, 16(5): 383-396.

[4] BEHZADIAN M, HOSSEINI-MOTLAGH S M, IGNATIUS J, et al. PROMETHEE group decision support system and the house of quality[J]. Group Decision and Negotiation, 2013, 22(2): 189-205.

[5] TAN R. Quality functional deployment as a conceptual aircraft design tool[D]. Singapore: Singapore Institute of Technology, 2000: 13-62.

[6] 解建喜, 宋筆鋒, 劉東霞. 飛機頂層設計中的模糊質量功能配置方法[J]. 機械工程學報, 2004, 40(9): 165-170.

XIE J X, SONG B F, LIU D X. Method of fuzzy quality function deployment in aircraft top-level design[J]. Journal of Mechanical, 2004, 40(9): 165-170 (in Chinese).

[7] 陳毅雨, 劉碩, 鐘斌, 等. 基于GQFD的警用反恐無人機戰績性能需求分析[J]. 火力與指揮控制, 2016, 41(9): 142-146.

CHEN Y Y, LIU S, ZHONG B, et al. Requirement analysis of police anti-terrorism unmanned aerial vehicle’s tactical performance based on GQFD[J]. Fire Control & Command Control, 2016, 41(9): 142-146 (in Chinese).

[8] 趙雷. 航空發動機低溫殼體設計需求分析與指標確定策略[J]. 航空發動機, 2017, 43(5): 91- 96.

ZHAO L. Design requirements analysis and indicators determination strategy of aeroengine cryogenic shell[J]. Aeroengine, 2017, 43(5): 91-96 (in Chinese).

[9] 張付英, 姜向敏, 王宏浩. 基于模糊理論的 QFD 用戶需求分析方法研究[J]. 天津科技大學學報, 2017, 32(1): 56-61.

ZHANG F Y, JIANG X M, WANG H H. Analysis method of customer requirements for QFD based on fuzzy theory[J]. Journal of Tianjin University of Science & Technology, 2017, 32(1): 56-61 (in Chinese).

[10] WANG J. Fuzzy outranking approach to prioritize design requirements in quality function deployment[J]. International Journal of Production Research, 1999, 37(4): 899-916.

[11] AKAO Y. New product deployment and quality assurance-quality deployment system[J]. Standardization and Quality Control, 1972, 25(4): 7-14.

[12] 邵家駿. 質量功能展開[J]. 航空標準化與質量, 1994(5): 9-15.

SHAO J J. Quality function deployment[J]. Aeronautic Standardization & Quality, 1994(5): 9-15 (in Chinese).

[13] 熊偉, 權婧雅. QFD及其發展動向[J]. 中國質量, 2008(10): 16-17.

XIONG W, QUAN J Y. Development trends of QFD [J]. China Quality, 2008(10): 16-17 (in Chinese).

[14] SILVERMAN M. HASS development methods: Screen development, change schedule, and re-prove schedule[C]∥Proceeding Annual Reliability and Maintainability Symposium, 2000, 43: 245-247.

[15] ZADEH L A. Fuzzy sets[J]. Information & Control, 1965, 8(3): 338-353.

[16] 劉雪杰. 兩種模糊數的排序方法及其應用研究[D].成都: 西南交通大學, 2014: 8-18.

LIU X J. Two ranking methods about fuzzy number and its application[D]. Chengdu: Southwest Jiaotong University, 2014: 8-18 (in Chinese).

[17] KAUFMANN A, Gupta M M. Fuzzy mathematical models in engineering and management science[M]∥Sole Distributors for the U.S.A. and Canada. Amsterdam: Elsevier Science Pub. Co., 1988: 37-103.

[18] 姜艷萍, 樊志平. 三角模糊數互補判斷矩陣排序的一種使用方法[J]. 系統工程, 2002, 20(2): 89-92.

JIANG Y P, FAN Z P. A practical ranking method for reciprocal judgment matrix with triangular fuzzy numbers[J]. Systems Engineering, 2002, 20(2): 89-92 (in Chinese).

[19] 李磊， 汪永超， 唐雨, 等. 基于模糊層次分析法的機械材料選擇[J]. 組合機床與自動化加工技術， 2015(11): 8-12.

LI L, WANG Y C, TANG Y, et al. Mechanical material selection based on FAHP[J]. Modular Machine Tool & Automatic Manufalturing Technique, 2015(11): 8-12 (in Chinese).

[20] 何楨, 趙有, 馬彥輝. 模糊QFD中技術重要度排序方法[J]. 天津大學學報, 2008, 41(5): 631-634.

HE Z, ZHAO Y, MA Y H. Method for rating technical characteristics in fuzzy QFD[J]. Journal of Tianjin University, 2008, 41(5): 631-634 (in Chinese).

[21] 錢存華, 張琳, 戴檳, 等. 三角模糊數的加權平均及其在評價決策中的應用[J]. 運籌與管理, 2005, 14(2): 5-9.

QIAN C H, ZHANG L, DAI B, et al. Fuzzy weighted average with triangular fuzzy numbers and its application to the assessment and decision[J]. Operations Research and Management Science, 2005, 14(2): 5-9 (in Chinese).

[22] 車阿大, 林志航, 方勇. 模糊集理論在QFD中的應用[J]. 系統工程理論方法應用, 1998, 7(2): 55-57.

CHE A D， LIN Z H， FANG Y. Study on using fuzzy sets in QFD[J]. Systems Engineering-Theory Methodology Applications, 1998, 7(2): 55-57 (in Chinese).

[23] TRAN L, DUCKSTEIN L. Comparison of fuzzy numbers using a fuzzy distance measure[J]. Fuzzy Set and Systems, 2002, 130(3): 331-341.

[24] 李賽, 周偉, 謝飛. 小型長航時太陽能無人機總體設計優化方法[J]. 空軍工程大學學報(自然科學版), 2018, 19(1): 7-15.

LI S, ZHOU W, XIE F. Overall design and optimization method of small long-endurance solar powered UAV[J]. Journal of Air Force Engineering University (Natural Science Edition), 2018, 19(1): 7-15 (in Chinese).