電動(dòng)力繩系離軌系統(tǒng)電流與拉力混合展開控制

黃靜，劉剛，朱東方，孫祿君

1.上海航天控制技術(shù)研究所，上海 201109 2.上海市空間智能控制技術(shù)重點(diǎn)實(shí)驗(yàn)室，上海 201109

自1957年第1顆人造衛(wèi)星升空以來，航天器應(yīng)用與人類社會(huì)的發(fā)展愈加緊密，但隨著進(jìn)入外層空間物體數(shù)量的不斷增加，空間碎片環(huán)境問題也越發(fā)突出。為了適應(yīng)空間探測的長期發(fā)展戰(zhàn)略，世界航天大國都已開始關(guān)注新型空間應(yīng)用技術(shù)。空間電動(dòng)力繩系離軌系統(tǒng)是一種典型的空間碎片主動(dòng)消除技術(shù)，該系統(tǒng)由在軌航天器、末端載荷及連接用的導(dǎo)電系繩構(gòu)成，工作原理為利用繞地運(yùn)行的導(dǎo)電纜繩切割地球磁場產(chǎn)生的動(dòng)生電動(dòng)勢，此時(shí)在系繩兩端分別安裝電荷采集和發(fā)射裝置即可有電流產(chǎn)生，與地磁場相互作用便產(chǎn)生了洛倫茲力，即電動(dòng)力[1]。與其他方法相比，空間電動(dòng)力繩具有能耗低、安全性高等優(yōu)點(diǎn)，是處理中低軌道太空垃圾的有效手段[2]。在任意空間電動(dòng)力繩任務(wù)中，都需要在發(fā)射至預(yù)定軌道后將系繩釋放到預(yù)定長度。

由于電-力耦合、重力梯度、環(huán)境攝動(dòng)等諸多因素存在，空間電動(dòng)力繩系統(tǒng)是一類典型的非線性系統(tǒng)，在變化地磁場及電離環(huán)境下會(huì)呈現(xiàn)不穩(wěn)定的動(dòng)力學(xué)行為，需要在釋放過程中對電動(dòng)力繩系統(tǒng)的姿態(tài)進(jìn)行控制[3]。目前，對于空間電動(dòng)力繩系統(tǒng)動(dòng)力學(xué)與控制技術(shù)正吸引著更多學(xué)者的密切關(guān)注，已產(chǎn)生了一些研究成果[4]。對于動(dòng)力學(xué)建模，Somenzi等[5]研究了帶有彈性的電動(dòng)力繩系在振動(dòng)和橫向振動(dòng)正則模態(tài)展開下的動(dòng)力學(xué)穩(wěn)定問題，對系統(tǒng)進(jìn)行動(dòng)力學(xué)分析，結(jié)果顯示姿態(tài)不穩(wěn)定來源于面外振動(dòng)角和電動(dòng)力的共振所產(chǎn)生的非零傾角。Zhong和Zhu[6]研究了長時(shí)離軌過程中采用裸線短系繩的電動(dòng)力繩系統(tǒng)的動(dòng)力學(xué)，考慮了由電動(dòng)力引起的軌道攝動(dòng)、大氣阻力、地球扁率等影響。Li和Zhu[7]提出了電動(dòng)力繩離軌過程中的珠點(diǎn)有限元模型，并應(yīng)用辛算法處理離散有限元模型中能量和動(dòng)量守恒問題，有限元法的缺點(diǎn)是計(jì)算量大，不易對動(dòng)力學(xué)方程進(jìn)行分析。潘偉等[8]采用在傅里葉空間描述的軌道動(dòng)力學(xué)模型,將控制量電流表示為傅里葉級數(shù)的形式，并推導(dǎo)了用傅里葉系數(shù)作為參量的橢圓軌道運(yùn)動(dòng)的平均軌道根數(shù)方程。

對于電動(dòng)力繩系統(tǒng)展開穩(wěn)定控制問題，由于空間繩系展開控制系統(tǒng)不僅是非線性的、典型的欠驅(qū)動(dòng)系統(tǒng)，還受到一些物理限制，比如拉力大小和電流強(qiáng)度都存在約束，這些給控制器的設(shè)計(jì)帶來了困難。已有文獻(xiàn)證明，通過拉力控制對于穩(wěn)定空間繩系系統(tǒng)的面內(nèi)運(yùn)動(dòng)是有效的。Rupp[9]首次嘗試?yán)孟道K長度及其變化速率穩(wěn)定系繩軌道平面的天平動(dòng)。近年來，Sun和Zhu[10]針對空間繩系系統(tǒng)展開控制問題設(shè)計(jì)了線性分?jǐn)?shù)階拉力控制律。由于以上文獻(xiàn)并沒有明確考慮非負(fù)的拉力限制，進(jìn)一步研究的學(xué)者們考慮系統(tǒng)的各種限制，采用基于優(yōu)化的方法，解決空間繩系的展開控制問題。例如，Steindl和Troger[11]在系繩拉力和長度變化速率的不等式約束條件下，針對空間繩系系統(tǒng)的面內(nèi)展開控制問題設(shè)計(jì)了最優(yōu)控制律。Wiliams[12]考慮了狀態(tài)和控制約束，在不同的性能指標(biāo)下設(shè)計(jì)了空間繩系面內(nèi)展開與回收的開環(huán)最優(yōu)控制律，并分別對有質(zhì)量彈性系繩與剛性系繩分別進(jìn)行建模與分析，說明了在控制律設(shè)計(jì)過程中，可以對彈性系繩進(jìn)行簡化，利用剛性系繩的展開回收控制律進(jìn)行修正以對實(shí)際系統(tǒng)進(jìn)行穩(wěn)定控制。Wen等[13]考慮空間繩系系統(tǒng)面內(nèi)展開控制問題，利用特殊的飽和函數(shù)處理拉力約束，提出了一種解析反饋控制律。

以上文獻(xiàn)僅考慮了系繩二維面內(nèi)展開的穩(wěn)定控制問題，針對三維空間繩系展開控制，在調(diào)節(jié)拉力或長度進(jìn)行控制基礎(chǔ)上，還需要另外一種推進(jìn)器與拉力進(jìn)行混合控制，以穩(wěn)定系繩的面外運(yùn)動(dòng)[14]。Kumar和Pradeep[15]利用拉力與面外推進(jìn)器混合控制，設(shè)計(jì)了一種線性反饋控制策略在較短時(shí)間內(nèi)穩(wěn)定了空間繩系的三維運(yùn)動(dòng)。在電動(dòng)力繩系統(tǒng)中，由于導(dǎo)電系繩與地磁場相互作用可以產(chǎn)生電動(dòng)力，利用調(diào)節(jié)電流與拉力穩(wěn)定電動(dòng)力繩系統(tǒng)展開時(shí)的面內(nèi)與面外運(yùn)動(dòng)可以充分發(fā)揮電動(dòng)力繩系的優(yōu)勢，不額外增加化學(xué)推進(jìn)裝置，很大程度節(jié)約了燃料。Wen等[16]采用啞鈴模型，忽略系繩質(zhì)量，基于能量方法設(shè)計(jì)了近地圓軌道運(yùn)行的三維電動(dòng)力繩系統(tǒng)展開拉力與電流反饋控制律，并分析了不同軌道傾角下的控制效果，滿足了控制要求，但控制律設(shè)計(jì)較為復(fù)雜。

本文主要考慮在近地橢圓軌道運(yùn)行的三維電動(dòng)力繩系統(tǒng)展開控制問題，僅通過調(diào)節(jié)系繩張力與電流，不依賴其他推進(jìn)器，將導(dǎo)電系繩釋放至期望長度并保持系統(tǒng)穩(wěn)定。在已有的文獻(xiàn)中，基本上都是忽略系繩質(zhì)量，但是在實(shí)際系繩展開過程中，幾千米的系繩存在一定質(zhì)量，且對展開過程中的系統(tǒng)質(zhì)心與等效質(zhì)量有一定影響，如果忽略會(huì)降低控制精度。因此，本文考慮系繩展開過程中系統(tǒng)質(zhì)心與等效質(zhì)量變化的影響，建立二體電動(dòng)力繩系衛(wèi)星系統(tǒng)動(dòng)力學(xué)模型。在控制方面，雖然已有文獻(xiàn)對于考慮控制約束的電動(dòng)力繩系統(tǒng)展開控制有一定研究，但基本上都是基于最優(yōu)控制方法。雖然最優(yōu)控制方法對于處理含約束的非線性控制問題非常有效，且能達(dá)到某些性能指標(biāo)的最優(yōu)，但是基于數(shù)值算法的最優(yōu)化計(jì)算效率較低，不利于實(shí)際應(yīng)用。因此，本文考慮系繩張力與電流存在約束的條件下，采用反步法結(jié)合抗飽和函數(shù)和輔助函數(shù)解決控制器受限問題，并引入動(dòng)態(tài)尺度廣義逆實(shí)現(xiàn)了對欠驅(qū)動(dòng)系統(tǒng)的穩(wěn)定控制。設(shè)計(jì)的姿態(tài)控制器保證了系統(tǒng)的穩(wěn)定性，達(dá)到了控制要求，具有潛在的應(yīng)用前景。

1 系統(tǒng)數(shù)學(xué)模型

1.1 電動(dòng)力繩系衛(wèi)星系統(tǒng)動(dòng)力學(xué)模型

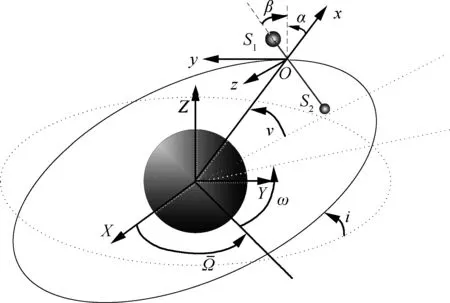
圖1 電動(dòng)力繩系衛(wèi)星系統(tǒng)示意圖Fig.1 Schematic of electro-dynamic tether satellite system

為簡化分析過程，作如下假設(shè)：系繩為質(zhì)量分布均勻的無彈性變形的剛性繩；系繩張力沿著繩的方向, 沒有法線方向的能量耗散；系繩兩端衛(wèi)星視為質(zhì)點(diǎn)，不考慮衛(wèi)星本體的姿態(tài)。

采用歐拉-拉格朗日方法對系統(tǒng)建模，根據(jù)歐拉-拉格朗日方程

(1)

(2)

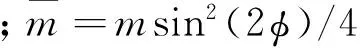
(3)

式中：md為釋放出的系繩質(zhì)量；ΛT=mT/m為系繩無量綱質(zhì)量；Λd=md/m為釋放出的系繩無維質(zhì)量。經(jīng)過推導(dǎo)，系統(tǒng)轉(zhuǎn)動(dòng)慣量Is為

(4)

因系繩釋放過程中，系統(tǒng)的轉(zhuǎn)動(dòng)慣量隨著繩長發(fā)生變化，經(jīng)過計(jì)算，轉(zhuǎn)動(dòng)慣量隨時(shí)間變化可以表示為

(5)

由于地球軌道半徑R遠(yuǎn)大于系繩長度，且μeR-1=Ω2R2，μe為地球引力常數(shù)，則系統(tǒng)勢能可以近似為

(6)

應(yīng)用拉格朗日第二定理求得系統(tǒng)的動(dòng)力學(xué)方程為

(7)

真近點(diǎn)角與地心半徑的關(guān)系可以寫為[17]

(8)

式中:e為軌道偏心率;p為軌道半通徑。下面對Qα和Qβ進(jìn)行計(jì)算，首先引入地磁場強(qiáng)度B=[Bx,By,Bz]T，由地球本體坐標(biāo)系下國際地磁參考場2000模型描述，這里采用較為精確的偶極子模型[18]，描述為

(9)

(10)

式中：

(11)

其中：I為系繩中的電流強(qiáng)度。為了方便計(jì)算，將方程進(jìn)行無量綱，得到如式(12)～式(14)所示的動(dòng)力學(xué)方程

(12)

(13)

(14)

式中:各導(dǎo)數(shù)為對無量綱時(shí)間τ的導(dǎo)數(shù)，d(·)/dt=Ωd(·)/dτ，ε=Ld/lc，lc為參考長度，設(shè)為系繩總長度。進(jìn)一步定義

(15)

根據(jù)式(9)和式(10)，可以求得式(15)中各參數(shù)為

(16)

Cα=[(h1cosi+sinicos2β)sinλ-

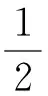
(17)

Cβ=[h2cosisinλ+(2cosusinα-

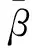
(18)

其中:

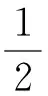
(19)

h2=2sinusinα+cosucosα

(20)

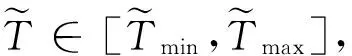
(21)

式中：

(22)

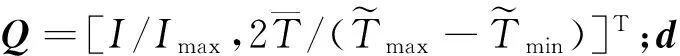
f(x1,x2)=

為了便于后面的控制器設(shè)計(jì)和穩(wěn)定性分析，首先給出一個(gè)引理。

引理1[19]: 對于任意ε>0,a∈R，下面的不等式成立

(23)

式中:δ為常數(shù)，滿足δ=e-(δ+1)，例如δ=0.278 5。

1.2 研究目標(biāo)

將針對1.1節(jié)所示的動(dòng)力學(xué)系統(tǒng)式(22)，考慮控制器輸出限制

‖Q‖∞≤1

(24)

在干擾d存在的情況下，目標(biāo)是通過合理的設(shè)計(jì)跟蹤控制器，使x1、x2趨近于期望狀態(tài)x1d、x2d。假設(shè)干擾d是有界的，即‖d‖∞≤dm，dm為估計(jì)的干擾上界。

2 控制器設(shè)計(jì)

2.1 抗飽和反步控制律設(shè)計(jì)

考慮到動(dòng)力學(xué)系統(tǒng)具有級聯(lián)形式，反步法具有設(shè)計(jì)過程簡單、可調(diào)參數(shù)較少、所得控制器物理意義明顯、可靠性好等優(yōu)點(diǎn)，因此下面將采用反步法，并結(jié)合抗飽和函數(shù)和輔助函數(shù)解決控制受限問題。

首先定義跟蹤誤差

e1=x1-x1d

(25)

構(gòu)造的Lyapunov函數(shù)為

(26)

將式(26)對時(shí)間求導(dǎo)，有

(27)

使閉環(huán)系統(tǒng)達(dá)到穩(wěn)定的虛擬控制量αv選取為

αv=-ce1-ξ

(28)

式中：c>0為可調(diào)節(jié)的常數(shù);ξ為防止控制輸入飽和而設(shè)計(jì)的的補(bǔ)償項(xiàng)，設(shè)計(jì)為[18]

(29)

其中:k2為正增益;ΔQ為實(shí)際控制輸入與飽和值的差，具體形式見式(32)～式(34)。進(jìn)一步定義

(30)

于是，通過式(25)和式(30)，可以得到誤差動(dòng)力學(xué)方程為

(31)

為了滿足控制受限的條件式(24)，實(shí)際的控制輸入Q為

Q=sat(Qs)

(32)

式中:Qs為期望的控制輸入、飽和函數(shù)sat(·)定義為

(33)

這里Qm=1，將式(29)中的ΔQ定義為

ΔQ=Q-Qs

(34)

下面設(shè)計(jì)控制器Qs，構(gòu)造增廣的類Lyapunov函數(shù)

(35)

式中：b>0為可調(diào)節(jié)的常數(shù)，反映了速度偏差的權(quán)重。對函數(shù)V2求時(shí)間導(dǎo)數(shù)，并進(jìn)行計(jì)算可得

(36)

由此可以看出飽和輸入Q被動(dòng)力學(xué)方程式(29)補(bǔ)償，進(jìn)一步設(shè)計(jì)Qs為

(37)

式中:g+(x1)∈R2×3表示控制系數(shù)矩陣g(x1)的廣義逆(Moore-Penrose)，即

g+(x1)=

(38)

式中：k1>0，k2>0為正常數(shù);N(e2)為抑制干擾所設(shè)計(jì)的函數(shù)，選取為

(39)

式中:ε>0為抑制干擾所設(shè)計(jì)的參數(shù)。將式(37)和式(39)代入式(36)，并根據(jù)引理1，則可以得到

(40)

于是可以推出

(41)

式中:kV=min(2c,2k1b)，ε1=δε，那么

(42)

可以看出，V2在可控范圍內(nèi)是非遞增的，由Barbalat引理[20]推論可知，e1和e2為一致最終有界的，最終收斂到0附近一個(gè)小臨域內(nèi)。

(43)

其對時(shí)間的導(dǎo)數(shù)為

(44)

當(dāng)k2>1/2，且ΔQ的模為有限值時(shí)，ξ可收斂并穩(wěn)定在一個(gè)包含零點(diǎn)的區(qū)域S內(nèi)，即

(45)

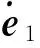
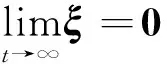
(46)

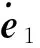
2.2 動(dòng)態(tài)尺度廣義逆引入

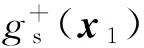
(47)

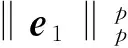
(48)

Q=sat(Qs)

(49)

(50)

總結(jié)上面的控制器設(shè)計(jì)過程以及穩(wěn)定性分析，可以得出以下定理。

本文提出的控制算法在實(shí)際應(yīng)用中需要獲取系繩面內(nèi)角、系繩長度及相應(yīng)的速度信息，可在兩星上安裝GPS、陀螺儀等測量衛(wèi)星的姿態(tài)，通過光電編碼器等測量系繩展開長度，利用“卷繞式”系繩釋放機(jī)構(gòu)，通過調(diào)節(jié)卷筒電機(jī)電壓的脈沖寬度產(chǎn)生拉力(阻力)以控制系繩釋放。并采用如空心陰極等離子接觸器調(diào)節(jié)系繩中的電流，以滿足控制的需要，使系統(tǒng)穩(wěn)定。

3 數(shù)學(xué)仿真分析

本節(jié)在MATLAB/SIMULINK環(huán)境下進(jìn)行數(shù)值仿真實(shí)驗(yàn)，驗(yàn)證本文所提出的控制算法的有效性。

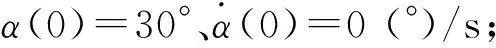
在實(shí)際情況中，電動(dòng)力繩系統(tǒng)在近地軌道附近受到的光壓力、氣動(dòng)阻力等干擾力無量綱值幅值不超過0.01，因此，外部干擾上限設(shè)為dm=0.01。

根據(jù)約束條件及控制精度，經(jīng)多次試驗(yàn)，控制參數(shù)選取為：c=1、b=5、k1=diag(5,5,0.3),k2=1。

仿真時(shí)間為無量綱時(shí)間τ=100，約為16個(gè)軌道周期。為了分析是否考慮系繩質(zhì)量對仿真結(jié)果的影響，本節(jié)分為系繩質(zhì)量為20 kg與0 kg兩種情況進(jìn)行仿真，仿真結(jié)果如圖2～圖8所示。

圖2 系統(tǒng)等效質(zhì)量隨時(shí)間變化曲線Fig.2 Variation curves of system equivalent mass vs time

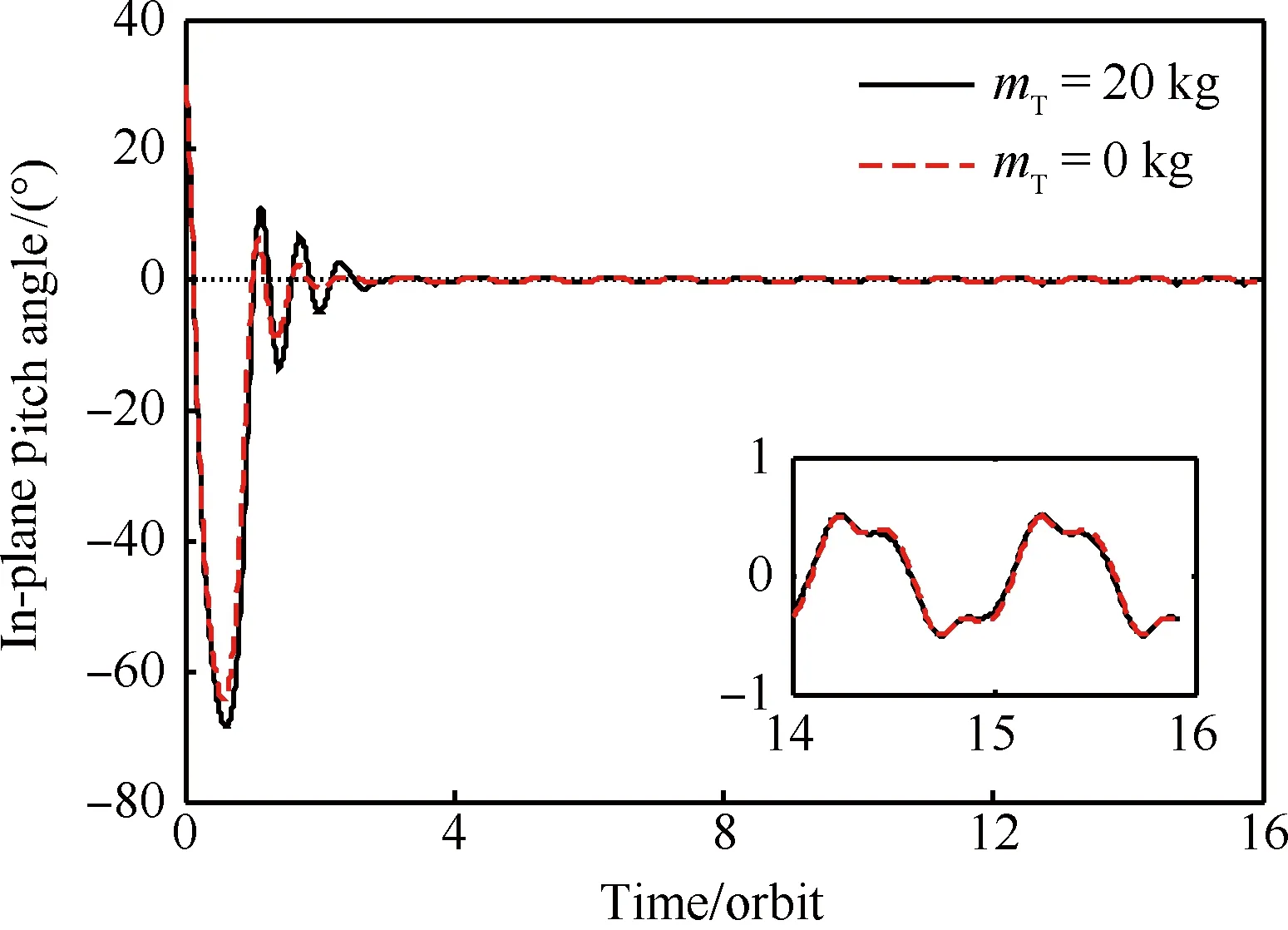
圖3 面內(nèi)俯仰角隨時(shí)間變化曲線Fig.3 Variation curves of in-plane pitch angle vs time

圖4 面外滾動(dòng)角隨時(shí)間變化曲線Fig.4 Viariation curves of out-plane roll angle vs time

圖2為電動(dòng)力繩系衛(wèi)星系統(tǒng)等效質(zhì)量隨時(shí)間變化曲線，可以看出系繩質(zhì)量對系統(tǒng)等效質(zhì)量的影響比較大，不考慮系繩質(zhì)量時(shí)系統(tǒng)等效質(zhì)量穩(wěn)定在29.126 2 kg，考慮系繩質(zhì)量時(shí)系統(tǒng)等效質(zhì)量隨系繩長度產(chǎn)生變化。圖3為面內(nèi)俯仰角隨時(shí)間變化曲線，可以看出在所提出的控制律作用下，面內(nèi)角在2個(gè)軌道周期左右收斂到0°附近，最大擺動(dòng)角約67°，在2個(gè)軌道周期后，面內(nèi)角在0°附近擺動(dòng)，由于動(dòng)態(tài)尺度廣義逆與廣義逆存在一定誤差，因此擺動(dòng)角在執(zhí)行機(jī)構(gòu)未達(dá)到飽和的情況沒有收斂到0°，擺動(dòng)周期約為1個(gè)軌道周期，幅度為0.5°，滿足在系繩展開過程中面內(nèi)角穩(wěn)定的要求。圖4為面外滾動(dòng)角隨時(shí)間變化的曲線，從圖4中可以看出，面外角振蕩幾次之后在2個(gè)軌道周期左右收斂到0°附近，在2個(gè)軌道周期后，面內(nèi)角在0.2°附近擺動(dòng)，擺動(dòng)周期約為0.5個(gè)軌道周期，幅度為0.3°，滿足在系繩展開過程中面外角穩(wěn)定的要求。圖5為系繩長度隨時(shí)間變化曲線，可以看出，系繩長度從初始的50 m平穩(wěn)地展開至5 000 m，2個(gè)周期后在拉力與電流的共同作用下維持在4 992 m附近，系繩最終長度誤差在0.2%以內(nèi)，滿足控制精度的要求。

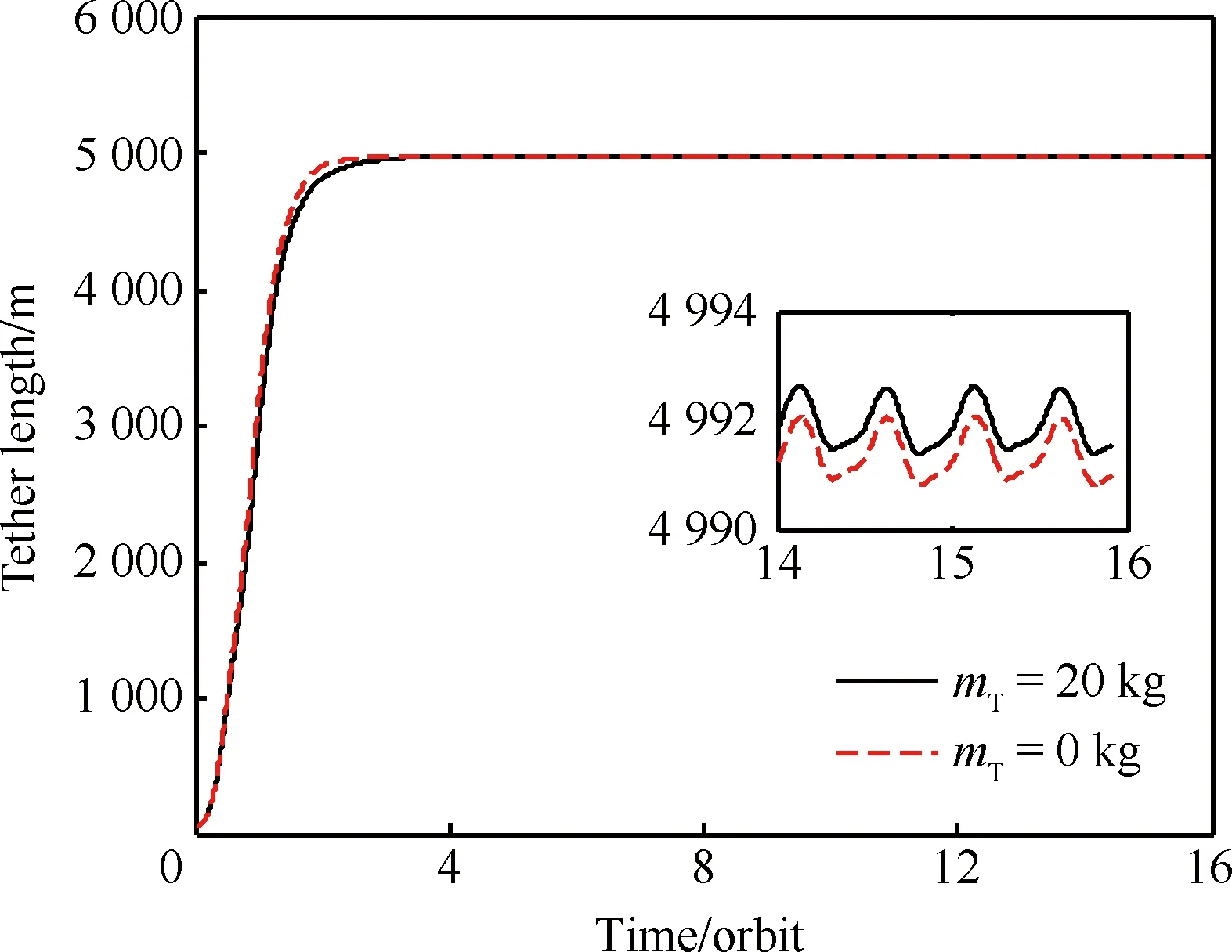
圖5 系繩長度隨時(shí)間變化曲線Fig.5 Variation curves of tether length vs time

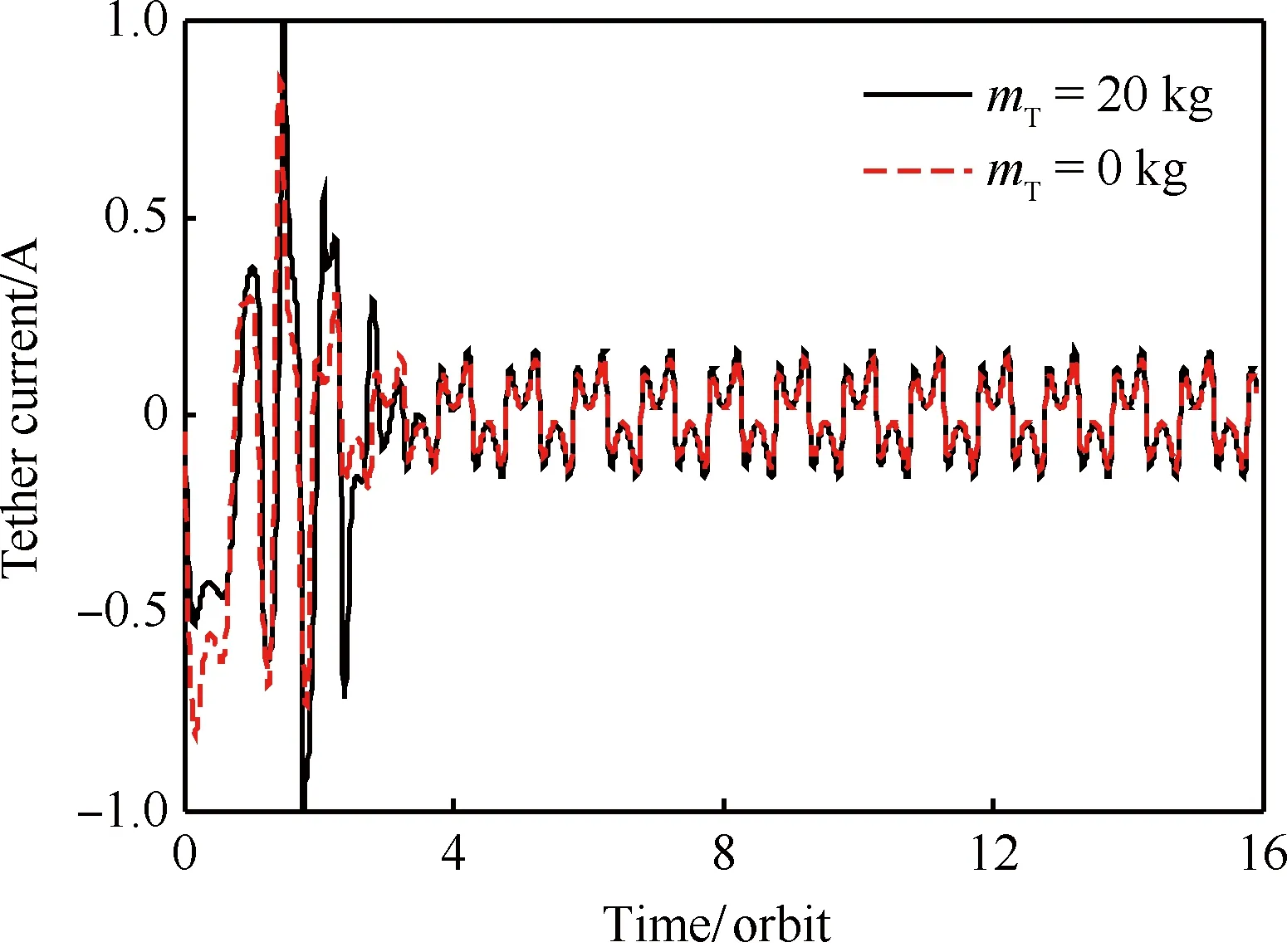
圖6 系繩電流隨時(shí)間變化曲線Fig.6 Variation curves of tether current vs time

圖8和圖9分別為兩種情況下16個(gè)軌道周期和最后兩個(gè)軌道周期內(nèi)的系繩末端在以母星(火箭末級等)為坐標(biāo)原點(diǎn)的軌道坐標(biāo)系下的變化軌跡。可以看出，釋放出的系繩末端在沿x方向釋放到4 992 m左右，并在穩(wěn)定后作小幅度周期性運(yùn)動(dòng)，表明是否考慮系繩質(zhì)量對系繩末端的三維運(yùn)動(dòng)影響不大。說明了在系繩電流、拉力受限以及攝動(dòng)影響的情況下，設(shè)計(jì)的欠驅(qū)動(dòng)反步控制器能保證整個(gè)閉環(huán)電動(dòng)力繩展開系統(tǒng)的一致最終有界穩(wěn)定性，充分驗(yàn)證了本文所提出的非線性控制器的有效性。

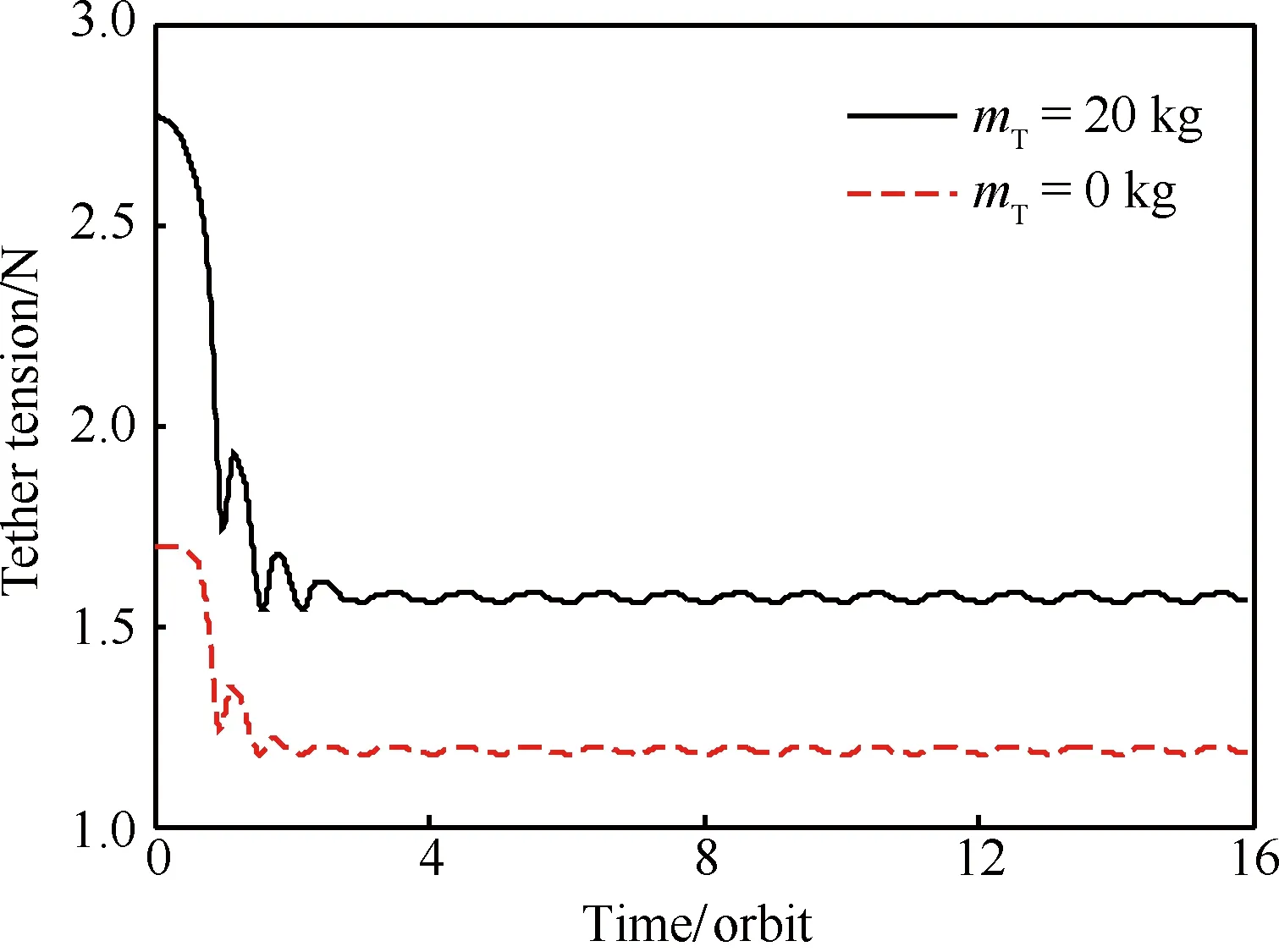
圖7 系繩拉力隨時(shí)間變化曲線Fig.7 Variation curves of tether tension vs time

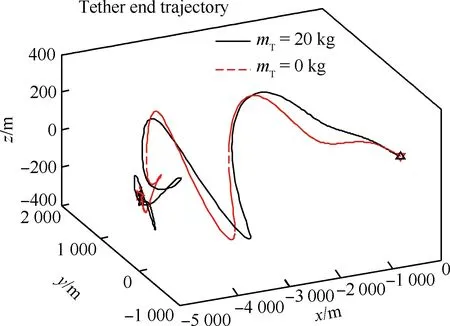
圖8 系繩末端在軌道坐標(biāo)系下變化軌跡Fig.8 Tether end trajectory in orbital coordinate frame

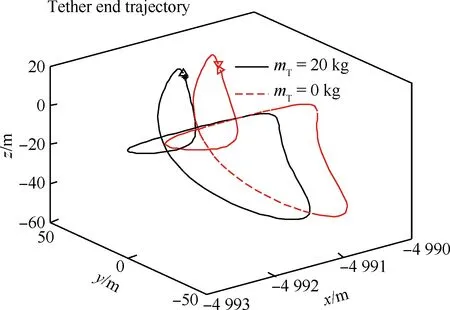
圖9 系繩末端在軌道坐標(biāo)系下變化軌跡 (最后兩個(gè)軌道周期)Fig.9 Tether end trajectory in orbital coordinate frame (the last two orbit periods)

4 結(jié) 論

本文針對近地軌道電動(dòng)力繩系統(tǒng)系繩展開控制問題，設(shè)計(jì)了一種僅通過調(diào)節(jié)系繩張力與電流的非線性欠驅(qū)動(dòng)電動(dòng)力系繩展開控制律。

1) 建立了考慮系繩質(zhì)量的近地軌道二體電動(dòng)力繩系衛(wèi)星系統(tǒng)動(dòng)力學(xué)模型，考慮了展開過程中系統(tǒng)質(zhì)心與等效質(zhì)量隨展開系繩長度的影響，減小了數(shù)學(xué)模型與實(shí)際系統(tǒng)的建模誤差。

2) 提出的控制算法僅通過調(diào)節(jié)系繩張力與電流，不依賴其它推進(jìn)器，將導(dǎo)電系繩釋放至期望長度并保持系統(tǒng)穩(wěn)定。

3) 考慮系繩張力與電流存在約束的條件下，提出了一種基于反步法結(jié)合抗飽和函數(shù)和輔助函數(shù)的控制律，并引入動(dòng)態(tài)尺度廣義逆實(shí)現(xiàn)了對欠驅(qū)動(dòng)系統(tǒng)的穩(wěn)定控制。仿真結(jié)果表明，系繩長度釋放至目標(biāo)長度，誤差保持在0.2%以內(nèi)，同時(shí)，系繩姿態(tài)面內(nèi)外角分別保持在小幅度擺動(dòng)，設(shè)計(jì)的姿態(tài)控制器保證了系統(tǒng)的穩(wěn)定性，達(dá)到了控制要求，具有潛在的應(yīng)用前景。

4) 在今后的研究中，將在此基礎(chǔ)上，進(jìn)一步考慮系繩撓性的影響，設(shè)計(jì)更加具有工程意義的控制律。

[1] SHIAH A, HWANG K S, WU S T, et al. Three-dimensional simulation of current collection in space[J]. Planetary and Space Science, 1997, 45(4): 475-482.

[2] PARDINI C, HANADA T, KRISKO P H. Benefits and risks of using electrodynamic tethers to de-orbit spacecraft[J]. Acta Astronautica, 2009, 64(5): 571-588.

[3] HOYT R P. Stabilization of electrodynamic tethers[C]∥Proceedings of 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Reston, VA: AIAA, 2002: 1-8.

[4] 蔡洪, 楊育偉, 郭才發(fā). 電動(dòng)力繩系研究進(jìn)展[J]. 宇航學(xué)報(bào), 2014, 35(11): 1223-1232.

CAI H, YANG Y W, GUO C F. Review of electrodynamic tether system[J]. Journal of Astronautics, 2014, 35(11): 1223-1232 (in Chinese).

[5] SOMENZI L, IESS L, PELAEZ J. Linear stability analysis of electrodynamic tethers[J]. Journal of Guidance, Control, & Dynamics, 2012, 28(5): 843-849.

[6] ZHONG R, ZHU Z H. Dynamics of nanosatellite deorbit by bare electrodynamic tether in low earth orbit[J]. Journal of Spacecraft & Rockets, 2015, 50(3): 691-700.

[7] LI G Q, ZHU Z H, Long-term dynamic modeling of tethered spacecraft using nodal position finite element method and symplectic integration[J]. Celestial Mechanics & Dynamical Astronomy, 2015, 123(4): 363-386.

[8] 潘偉, 路長厚, 李吉棟, 等. 基于傅里葉展開的電動(dòng)力繩系衛(wèi)星最優(yōu)控制[J]. 航空學(xué)報(bào), 2011, 32(9): 1714-1721.

PAN W, LU C H, LI J D, et al. Optimal control of electrodynamic tethered satellites based on Fourier series expansion[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1714-1721 (in Chinese).

[9] RUPP C C. A tether tension control law for tethered subsatellites deployed along local vertical: NASA-TM-X-64963[R]. Wahsington, D.C.: NASA, 1975, 1-28.

[10] SUN G H, ZHU Z H. Fractional-order tension control law for deployment of space tether system[J]. Journal of Guidance, Control, & Dynamics, 2014, 37(6): 2062-2066.

[11] STEINDL A, TROGER H. Optimal control of deployment of a tethered subsatellite[J]. Nonlinear Dynamics, 2003, 31(3): 257-274.

[12] WILLIAMS P. Optimal deployment/retrieval of tethered satellites[J]. Journal of Spacecraft & Rockets, 2008, 45(2): 324-343.

[13] WEN H, ZHU Z H, JIN D P, et al. Space tether deployment control with explicit tension constraint and saturation function[J]. Journal of Guidance, Control, & Dynamics, 2016, 39(4): 915-920.

[14] STEINDL A, Optimal control of the deployment (and retrieval) of a tethered satellite under small initial disturbances[J]. Meccanica, 2014, 49(8): 1879-1885.

[15] KUMAR K, PRADEEP S. Strategies for three dimensional deployment of tethered satellites[J]. Mechanics Research Communications, 1998, 25(5): 543-550.

[16] WEN H, JIN D, HU H. Three-dimensional deployment of electro-dynamic tether via tension and current control with constraints[J]. Acta Astronautica, 2016, 129: 253-259.

[17] VALLADO D A. Fundamental of astrodynamics and applications[M].New York: Microcosm Press, 2007: 103-117.

[18] WILLIAMS P. Libration control of electrodynamic tethers using predictive control with time-delayed feedback[J]. Journal of Guidance, Control, & Dynamics, 2015, 32(4): 1254-1268.

[19] POLYCARPOU M M, IOANNOU P A. A robust adaptive nonlinear control design[J], Automatica, 1996, 32(3): 423-427.

[20] SLOTINE J J E, LI W. Applied nonlinear control[M]. Beijing: China Machine Press, 2004: 121-155.

[21] 黃靜, 李傳江, 馬廣富, 等. 基于廣義逆的欠驅(qū)動(dòng)航天器姿態(tài)機(jī)動(dòng)控制[J]. 自動(dòng)化學(xué)報(bào), 2013, 39(3): 285-292.

HUANG J, LI C J, MA G F, et al. Generalised inversion based maneuver attitude control for underactuated spacecraft[J]. Acta Automatica Sinica, 2013, 39(3): 285-292 (in Chinese).