片間綜合化互連時間觸發(fā)通信調度方法
孔韻雯,李峭, *,熊華鋼,程子敬
1.北京航空航天大學 電子信息工程學院,北京 100083 2.北京衛(wèi)星信息工程研究所,北京 100080
綜合化航空電子系統(tǒng)經(jīng)歷了分立式、聯(lián)合式、綜合式到高度綜合的發(fā)展過程[1-2],目前,高度綜合的分布式綜合模塊化航空電子(Distributed Integrated Modular Avionics, DIMA)體系結構,其特征在于利用分布式架構將所有綜合化模塊分布在整個飛行器中[3],通過時間確定網(wǎng)絡實現(xiàn)安全關鍵性消息的嚴格周期確定性。文獻[4]提到未來航電系統(tǒng)計算體系結構向著智能化、多核處理、微內核和片上系統(tǒng)(System on Chip, SoC)的方向發(fā)展。更進一步,隨著可綜合模塊微小型化的發(fā)展,例如:美國國防高級研究計劃局(DARPA)的MTO辦公室推出新型片內微結構的研究項目[5],歐洲e2V公司推出了幾百克重的航電多核處理機[6],微小型智能片間互連系統(tǒng)有望成為未來航空航天電子系統(tǒng)分布式綜合對象。
迄今為止航電綜合化互連技術屬于局域網(wǎng)(LAN)或系統(tǒng)域網(wǎng)(SAN)范疇,尚未出現(xiàn)廣為認可的跨越處理核內部總線、外部局部總線、I/O總線、SAN和LAN等計算體系結構[7]層次的互連技術。針對微小型智能片上系統(tǒng)亟待解決的片間互連問題,串行外設接口(SPI)和Rapid-IO支持的最大速率雖然遠高于I2C的5 Mbit/s[8-9],但是沒有提供固定規(guī)則的尋址方案和數(shù)據(jù)流量控制[10],基于SPI總線和Rapid-IO的消息傳輸尋址都需要設計人員的特定規(guī)劃。考慮到未來應用遷移的方便性,本文采用開放性介質無關接口實現(xiàn)芯片間互連,滿足跨體系結構層次互連的功能一致性。
對于跨越微小型智能器件的綜合化互連系統(tǒng),文獻[11]研究了混合關鍵性系統(tǒng)分布式實時架構,通過時間觸發(fā)以太網(wǎng)(Time-Triggered Ethernet, TTE)實現(xiàn)了多個多核芯片互連的跨層次體系結構,其側重于該架構下的可重配置方法。文獻[12]研究了片上和片間跨層次體系結構模型,并分別將基于靜態(tài)調度表和基于優(yōu)先級的兩種調度方法應用于該模型,但前者會引入調度切換開銷,后者由于不同層次結構中流量約束優(yōu)先級不同,可能會對可組合性產生影響。更有甚者,文獻[13-14]提出了時間觸發(fā)片上系統(tǒng)(Time-Triggered System on Chip, TTSoC)架構,通過時間觸發(fā)片上網(wǎng)絡[15](Time-Triggered Network-on-Chip,TTNoC)實現(xiàn)片上多個異構IP塊的互連,但與底層硬件聯(lián)系緊密。
得益于時間觸發(fā)網(wǎng)絡中TT流量調度方法的積累,可以為片間互連網(wǎng)絡拓撲中TT流量的調度方法提供參考。如:文獻[16-17]采用可滿足模理論(Satisfiability Modulo Theories, SMT)求解器,通過網(wǎng)絡拓撲和流量配置進行約束,生成滿足約束的TT網(wǎng)絡時間觸發(fā)調度表;文獻[18]則提出了利用最早期限(EDF)算法調度異步任務的增量化調度方法;文獻[19]綜合考慮了時間觸發(fā)控制器處理和通信的約束關系,但片間互連往往是多網(wǎng)段分布式交換結構,無法直接應用上述總線調度結果。對于更細粒度的片間TT流量調度,文獻[20-21]基于特征任務的嚴格周期性任務可調度分析方法可供借鑒。
另外,對于端系統(tǒng)主機組成的TTE網(wǎng)絡,雖然TT流量的單跳交換延遲為μs量級,但應用層事件觸發(fā)和時間觸發(fā)機制配合的等待時間甚至達到流量周期的量級,TTTech公司的操作系統(tǒng)中間件[22]可以部分解決上述問題;但對于片上系統(tǒng)組成的網(wǎng)絡,應用的操作環(huán)境是輕量化的,很難在源、宿節(jié)點嵌入純軟件實現(xiàn)的中間件,且具有多級交換轉發(fā),為了保證各物理鏈路上TT流量的嚴格實時性,只得將等待時間分散于各交換節(jié)點。
本文的貢獻在于建立基于開放性介質無關接口的芯片間綜合化互連模型,并在現(xiàn)有嚴格周期性任務可調度分析方法[20-21]的基礎上,提出一種應用于片間互連的TT通信調度方法。本方法采用負載均衡的選徑方法,以盡量減小等待時間為目標確定流量的發(fā)送時間偏移量,并利用遺傳算法優(yōu)化發(fā)送端口的調度表相位,獲得具有全局意義的時間觸發(fā)調度表。
1 片間綜合化互連模型
1.1 片間互連的拓撲結構
在電路板范圍內,芯片之間通過開放式的介質無關接口建立物理鏈路,進行全雙工通信。芯片的物理鏈路數(shù)量和布局根據(jù)數(shù)據(jù)傳輸?shù)男枨蟠_定,在一般情況下是不對稱的。取代獨立的中心交換機的交換結構也通常不對稱,分別就近嵌入于芯片端口內的可編程結構中。選定某一芯片作為片間互連的網(wǎng)關,通過連接板外交換機節(jié)點進行跨電路板消息的端到端傳輸。
將一個芯片間互連結構記為G=(V,E),V={vi}表示各個芯片,E={ei}表示芯片間的雙向連接路徑。芯片之間的通信是全雙工的,相鄰芯片間的物理連接可以根據(jù)不同的方向標記為不同的通信鏈路,用L={li}表示板上通信鏈路的集合。若vi、vj∈V為相鄰節(jié)點,則(vi,vj)∈L表示vi到vj的通信鏈路;(vj,vi)∈L表示vj到vi的通信鏈路。
對于給定芯片vs、vd∈V間的端到端通信,從vs到vd傳輸路徑可以表示為
p=((vs,vi),…,(vj,vd))
式中:vs為源節(jié)點;vd為目的節(jié)點;其他芯片為中轉節(jié)點,角標i和j為芯片編號。此外,規(guī)定流量傳輸路徑不會構成回環(huán)。
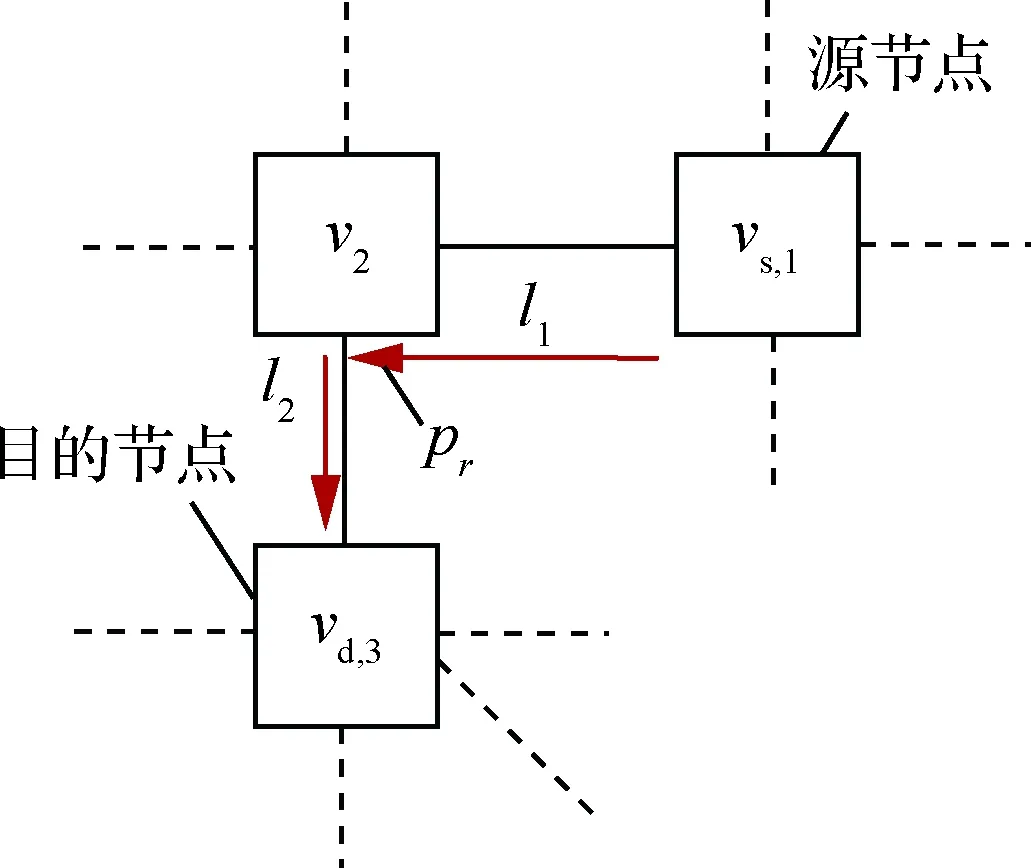
圖1為局部芯片互連拓撲示例,選擇v6作為板上網(wǎng)關節(jié)點。圖中所示為傳輸路徑:e1和e2分別為v1、v2和v1、v5之間的雙向連接通信路徑;v5為中轉節(jié)點,包含鏈路l1=(v5,v4)的發(fā)送端口。
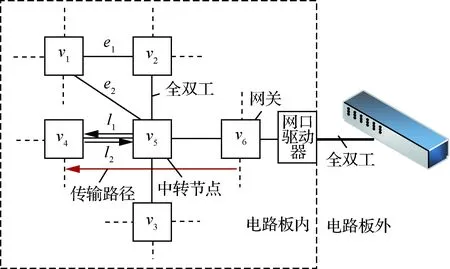
圖1 局部芯片互連拓撲Fig.1 Topology of local chip interconnection
1.2 時間觸發(fā)流量片間通信模型
假設片間通信的TT流量集合為F=(f1,f2,…,fn),每條流量都由芯片產生或是由網(wǎng)關轉發(fā)進入板內,用4組元fi=〈Pi,Ti,ci,pi〉(1≤i≤n)表示,Pi為流量的優(yōu)先級,本文中規(guī)定跨板流量具有最高優(yōu)先級,周期具有次高優(yōu)先級,周期越小優(yōu)先級越高;Ti和ci分別為周期和執(zhí)行時間;pi為傳輸路徑,包含了q(q≥1)段通信鏈路,源節(jié)點為vs,i,目的節(jié)點為vd,i,經(jīng)過的跳數(shù)為h=q+1。流量傳輸路徑可以由設計根據(jù)需求靜態(tài)離線確定,對于沒有確定路徑的流量,將在2.1節(jié)中說明根據(jù)負載均衡原則確定路徑的方法。
芯片之間需要進行時鐘同步,專用同步線是可選的近距離時鐘同步的簡易方法;然而,考慮到抗摧毀能力和未來應用遷移所需的開放性,利用片上的可編程資源實現(xiàn)壓縮主控器(Compress Master,CM)、同步主控器(Synchronization Master,SM)和同步客戶端(Synchronization Client,SC),通過協(xié)議控制幀(Protocol Control Frame, PCF)實現(xiàn)各個芯片間的時鐘同步,形成符合SAE AS6802標準[23]的同步過程,使之不僅在本地電路板上實現(xiàn)同步,而且可以與滿足該標準的時間觸發(fā)網(wǎng)絡實現(xiàn)同步。目前,對于100 Mbps碼速率的TTE,分布式同步精度為1 μs。此外,TT流量通信過程有以下規(guī)則:
1) 各個芯片端口發(fā)送的TT流量均滿足嚴格周期性,即同一個TT流量的兩個連續(xù)消息之間的時間間隔是固定的,且等于周期。
2) 本調度方法中規(guī)定選定作為網(wǎng)關的片上系統(tǒng)不作為消息傳輸路徑中的中轉節(jié)點中繼轉發(fā)消息。
3) 跨板流量具有最高的優(yōu)先級,在所有等待調度的TT流量中優(yōu)先被安排。
1.3 嚴格周期任務的可調度性
如果將時間觸發(fā)流量的傳輸服務作為任務,傳輸延遲作為任務的“執(zhí)行”時間,則也可借鑒多處理器任務集合可調度性的判定方法。在下面的討論中,令“任務”與TT流量的含義相同,而消息作為流量的實例,相當于任務的“作業(yè)”。
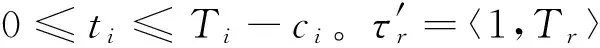
此外,用函數(shù)LLC(S)表示一個非空集合S中連續(xù)整數(shù)的最長長度,函數(shù)SLC(S,l)表示一個非空集合S中長度大于l的連續(xù)整數(shù)中的最小整數(shù)[20],函數(shù)LC(S)表示一個非空集合S中各段連續(xù)整數(shù)的長度。
1) 利用原任務的特征任務,采用取模運算求出Tr上被任務τi占用的時間ITU(i,r)。
2) 求出特征任務在可調度時的所有空余時間。
3) 計算特征任務可用空余時間的最大長度,判斷任務的可調度性。
定理1[20-21]任務τr=〈cr,Tr〉與集合T中所有任務是可調度的,當且僅當:
cr≤LLC(QT(r))
(1)
式中:LLC(QT(r))為空余時間QT(r)的最長長度。
2 TT流量調度方法
片間互連的TT流量調度方法在1.3節(jié)嚴格周期任務可調度性判定方法的基礎上,調度得到由分布于各端口的循環(huán)調度表組成的全局時間觸發(fā)調度表。該方法主要有以下3個步驟:
1) 利用基于特征任務的可調度性分析,計算端口負載率,根據(jù)負載均衡原則確定流量傳輸路徑。
2) 以等待時間局部最優(yōu)為目標,依據(jù)優(yōu)先級排序以增量化方式初步確定流量發(fā)送時間偏移量,獲得各端口的循環(huán)調度表。
3) 利用遺傳算法調整各端口調度表相位,更新流量在各端口發(fā)送時間偏移量,得到全局優(yōu)化意義的時間觸發(fā)調度表。
2.1 流量傳輸路徑的選擇
對于TT流量跳數(shù)相同的可能端到端路徑,以負載均衡為目標選擇流量傳輸路徑。為了提高路徑選擇算法的效率,采用廣度優(yōu)先,在不產生回環(huán)路徑的前提下,逐級搜索可能經(jīng)過的通信鏈路,判定TT流量在通信鏈路發(fā)送端口的可調度性。若存在無法調度的端口,則通過“剪枝”,剔除包含該端口所在傳輸路徑。通過累加計算可行端到端路徑的流量負載率,選擇負載率最小的路徑為流量的傳輸路徑。
2.1.1 TT流量可調度性判定算法
參考1.3節(jié)嚴格周期任務的可調度性判定多次和定理1[20-21],算法1用于判定TT流量在通信鏈路li發(fā)送端口的可調度性,其計算的時間復雜度為O(NTmax),Tmax為流量集合里的最大周期。
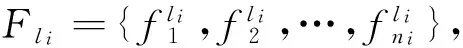

算法1 TT流量可調度性判定算法 輸入:TT流量集合Fli={fli1,fli2,…,flini}和待判定流量fr=
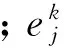
(2)
(3)
2.1.2 TT流量通信路徑選擇算法
采用廣度優(yōu)先算法,搜索得到待安排路徑流量fr=〈Pr,Tr,cr,pr〉可能的k條端到端傳輸路徑集合Rr=(p1,p2…,pk),以及所有可能路徑中包含的q段物理鏈路li(1≤i≤q)。
算法2用于選擇TT流量的通信路徑,在算法1的基礎上先判定鏈路的可調度性,在剔除包含不可調度的鏈路的路徑后,選擇負載率最小的可行端到端路徑為流量的傳輸路徑,其計算的時間復雜度為O(N2)。算法2的偽代碼如下。

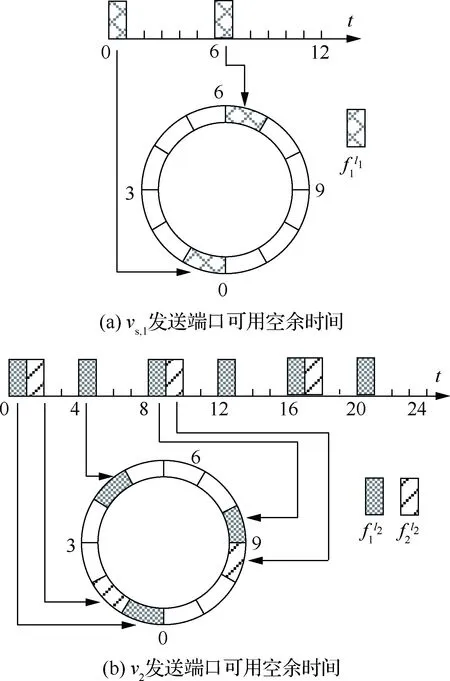
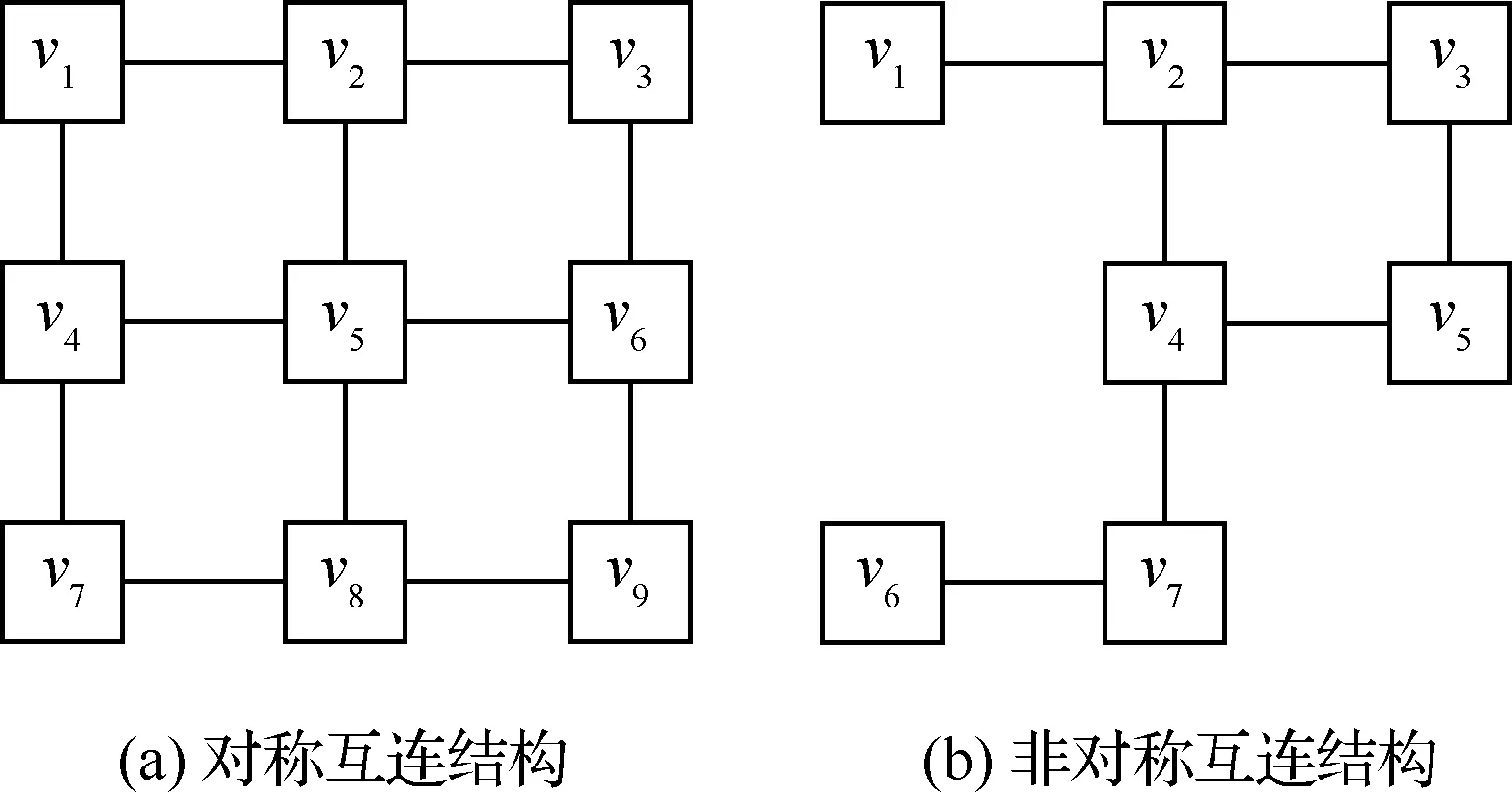
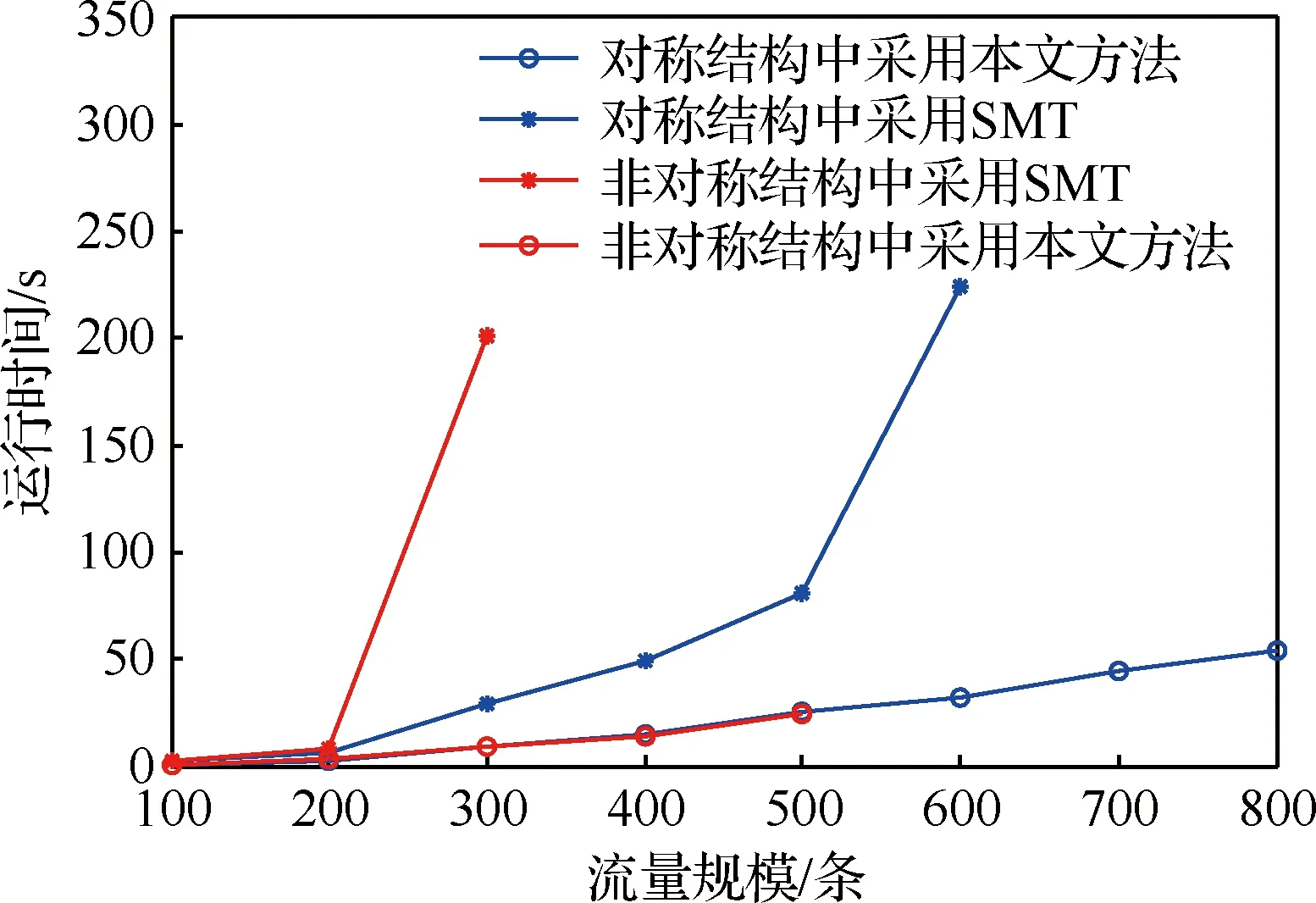
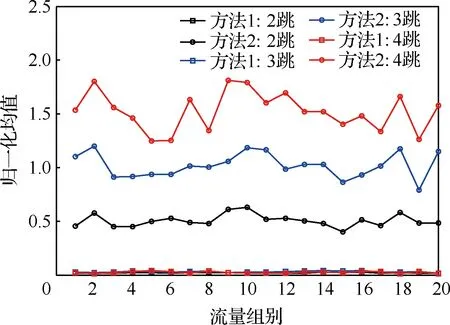
算法2 TT流量通信路徑選擇算法 輸入:TT流量集合Fli=fli1,fli2,…,flini{},待安排流量fr= 其中:A為預先根據(jù)可能負載率設定的較大常數(shù);Uli為鏈路li發(fā)送端口的負載率,即 (4) 2.2.1 發(fā)送時間偏移量的初步確定 在片間的傳輸過程中,對流量傳輸?shù)亩说蕉搜舆t影響最大的是流量在中轉節(jié)點等待發(fā)送的緩存時間,記流量fr在傳輸路徑pr的等待時間為wtr(pr),流量fr在中轉節(jié)點vi(li=(vi,vj))等待時間為wtr(li),表示流量fr在到達vi后等待發(fā)送的時間。對于包含q段通信鏈路的路徑pr,wtr(pr)由wtr(li)累加得到,即 wtr(pr)= wtr(l2)+wtr(l3)+…+wtr(lq) (5) 對于靜態(tài)調度的流量,在發(fā)送節(jié)點端口的發(fā)送時間偏移量為 (6) 在中轉節(jié)點端口的發(fā)送時間偏移量為 (7) 圖3給出了例1根據(jù)算法1計算得到的結果,其中圖3(a)給出了vs,1發(fā)送端口可用的空余時間;圖3(b)為中轉節(jié)點v2發(fā)送端口可用的空余時間。 由此得到,fr中的消息在路徑pr的最小可行等待時間wtr(pr)=wtr(l2)=2。 圖2 消息傳輸路徑Fig.2 Message transfer path 圖3 消息等待時間計算過程Fig.3 Calculation process for message waiting time 2.2.2 等待時間的優(yōu)化 發(fā)送端口的循環(huán)調度表決定了該輸出物理鏈路上TT流量的嚴格周期性,而且各個循環(huán)調度表之間的相對相位影響了消息的等待時間。為了縮短最壞情況下的等待時間,采用遺傳算法[24-25]調整芯片各發(fā)送端口的調度表相位,得到各端口近似最優(yōu)的一組相位值。 給定相位值后,各流量在發(fā)送端口的偏移量依次循環(huán)移位更新,得到全局優(yōu)化意義的時間觸發(fā)調度表,此時最壞情況下的最大等待時間最短。 當一代相位確定后,代入式(8)進行各端口流量fr=〈Pr,Tr,cr,pr〉的發(fā)送時間偏移量的更新 (8) 偏移量更新后,采用式(8)計算等待時間,進而得到其中的最大等待時間wtmax。從優(yōu)化目標可知,wtmax越大,遺傳算法中基因保留在子代的可能性越小,因此設置適應度函數(shù)為 (9) 式中:Cmax為預先根據(jù)可能結果設定的較大常數(shù)。 根據(jù)父代個體所得的適應度值降序的排列,利用選擇算子和交叉算子生成子代,經(jīng)過多代遺傳后適應度函數(shù)收斂,從而得到近似的最優(yōu)值。 設基于芯片間消息實際傳輸速率為100 Mbit/s,以太網(wǎng)幀的幀長范圍為64~1 518字節(jié),則每一幀傳輸?shù)膱?zhí)行時間范圍為5.12~121.44 μs,TT流量的周期通常為1~128 ms。考慮到仿真主要是為了驗證該調度方法的有效性,需要在逼真度和計算復雜度之間取得權衡,因此將消息的執(zhí)行時間和周期以μs為單位進行上取整為cr∈[6,122],且cr∈N;在工程中,取整后增加的冗余量可作為消息的保護間隔。為了在仿真中使各流量的周期存在一定的公約數(shù)關系且具有多樣性,使Ti=2n×3m×1 000,其中0≤n≤7,0≤m≤2,且Ti∈[1 000,128 000]。 仿真規(guī)模對應于3×3網(wǎng)格式的實驗原型,該原型可配置為對稱互連結構及非對稱互連結構,分別如圖4(a)和圖4(b)所示。 為了進行對比,其對照組利用SMT工具求解各端口調度表[16-18],值得說明的是,現(xiàn)有SMT工具僅面向端系統(tǒng)主機之間的互連,計算中將“端系統(tǒng)”等效為芯片的發(fā)送端口,“交換機”等效于芯片內部的交換結構,但規(guī)定連接于同一“交換機”的“端系統(tǒng)”間不產生外部通信流量。 類似于文獻[16],SMT的單跳延遲下界設置為122 μs(最長幀執(zhí)行時間),不可判定情況下的停機時間為1.5 h,但為了允許中轉節(jié)點緩沖等待,將單跳延遲上界設為最長幀的4倍(文獻[16]中的最大選項)。 針對對稱與不對稱的互連結構,調度規(guī)模如表1所示,分別采用SMT和本文提出的調度方法得到各組流量中的最大等待時間。其中,對稱和非對稱結構中的最大等待時間分別記為wtmax,S和wtmax,A,以μs為單位,“--”表示SMT不可判定超時。 由仿真結果可以看出,在兩種結構中,當規(guī)模較小時,兩種方法調度得到的等待時間相近;而流量規(guī)模較大時,利用SMT進行調度的傳輸?shù)却龝r間較小于本文調度方法得到的等待時間,但本文調度方法的可調度流量規(guī)模相較于SMT至少增加30%。 圖4 對稱和非對稱互連拓撲結構Fig.4 Topology structure of symmetrical and asymmetrical interconnection 表1 可調度流量規(guī)模Table 1 Scheduled message size 流量規(guī)模SMT本文方法wtmax,S/μswtmax,A/μswtmax,S/μswtmax,A/μs1001085133378489420018672039601224830016592437152238794001856--236059735002133--373396296002273--3638不可調度700----3800不可調度800----5294不可調度 此外,與SMT相比,本調度方法可以明確得到不可調度的結論,且導致不可調度的流量明確,便于根據(jù)實際調度情況及時調整。 對照組采用Yices SMT求解器,核心算法為優(yōu)化后的同余閉包算法[26],其時間復雜度為O(N3lgN),然而,當它具體應用于TT調度問題時,會出現(xiàn)非線性的離散數(shù)學約束,即使僅搜索可行解,也被認為是NP問題[18]。對于本文提出的調度方法,依次執(zhí)行算法1和算法2即可得到可行解,整體時間復雜度為O(N2)。在對稱與非對稱拓撲結構中,SMT與本文提出的調度方法對流量進行調度規(guī)劃的運行時間如圖5所示,本方法對流量進行調度規(guī)劃的時間遠小于SMT,并且在對稱與非對稱結構中,流量規(guī)模的增加并不會導致調度規(guī)劃的時間明顯增長。 圖5 運行時間對比Fig.5 Comparison of execution time 利用20組600條TT流量,對比本文提出的逐跳計算流量的發(fā)送時間偏移量方法(方法1)和文獻[20]中既有的基于特征任務的調度方法(方法2)對等待時間的影響。 以流量傳輸?shù)却龝r間占周期的比例作為歸一化的傳輸延遲度量,圖6為分別為采用兩種方法調度2~4跳流量的平均傳輸延遲;其中10組仿真結果中,每組流量中的最大等待時間wtmax及對應的歸一化傳輸延遲見表2。 在不經(jīng)過遺傳算法優(yōu)化前方法1得到的傳輸延遲不超過0.01,流量等待時間沒有隨著傳輸跳數(shù)的增加而明顯增加,而方法2得到的傳輸延遲至少為1.99,傳輸路徑每增加1跳,等待時間顯著增加。本方法與既有的基于特征任務的調度方法相比,傳輸延遲縮短到后者的2%以下,得到每條流量的局部最優(yōu)等待時間。 圖6 等待時間歸一化均值Fig.6 Normalized average of message waiting time 表2 最大等待時間Table 2 Maximum waiting time 流量組別方法1方法2wtmax/μswtmaxTi跳數(shù)wtmax/μswtmaxTi跳數(shù)126110.01942868732.994244490.03532868552.994328940.05422869902.994431420.03332559432.004527650.02231917052.004626690.02122551421.993736400.03732559182.004831970.03332872182.994929320.02032569112.0041030330.02432558442.004 針對3.1節(jié)非對稱結構中調度的一組500條TT流量,利用方法1調度得到的最大等待時間為11 173 μs,利用方法2調度得到的最大等待時間為25 8133 μs。采用遺傳算法優(yōu)化兩種方法調度得到的最大等待時間,其優(yōu)化結果如圖7所示。 方法1得到的最大等待時間經(jīng)過遺傳算法優(yōu)化后為9 645 μs,優(yōu)化了13.7%,方法2得到的最大等待時間經(jīng)過1 672代的遺傳迭代優(yōu)化后,盡管該方法調度流量中的最大等待時間在優(yōu)化后減小了35.8%,仍然遠大于方法1得到的最大等待時間,進一步驗證了本文方法能夠縮短流量傳輸?shù)却龝r間這一優(yōu)勢。 圖7 方法1和方法2最大等待時間優(yōu)化過程Fig.7 Optimization process of maximum waiting time for Methods 1 and 2 1) 本文建立了可以用于片間、片上系統(tǒng)和模塊聯(lián)合工作的片間綜合化互連結構模型,提出了適用于該結構的一種TT通信調度方法,其將縮短等待時間作為優(yōu)化目標,規(guī)劃流量傳輸路徑,選擇并調整流量發(fā)送時間偏移量,獲得具有全局最優(yōu)意義的時間觸發(fā)調度表,并通過了案例仿真進行驗證。 2) 本方法能夠在有限時間內得到是否可調度的判定結論;通過案例研究,對于可調度的情況,本方法的可調度流量規(guī)模比SMT方法至少增加了30%;即使不可調度,本方法能夠明確指出導致不可調度的流量,便于快速設計調整。 3) 案例研究結果表明,以流量傳輸?shù)却龝r間占周期的比例作為歸一化的傳輸延遲度量,本方法得到的傳輸延遲小于0.01,與既有的基于特征任務的調度方法相比,縮短到后者傳輸延遲的2%以下。 [1] 熊華鋼, 王中華. 先進航空電子綜合技術[M]. 北京: 國防工業(yè)出版社, 2009: 2-13. XIONG H G, WANG Z H. Advanced avionics integration techniques[M]. Beijing: National Defense Industry Press, 2009: 2-13 (in Chinese) [2] 王國慶, 谷青范, 王淼, 等. 新一代綜合化航空電子系統(tǒng)構架技術研究[J]. 航空學報, 2014, 35(6): 1473-1486. WANG G Q, GU Q F, WANG M, et al. Research on the architecture technology for new generation integrated avionics system[J]. Acta Aeronautica et Aastronautica Sinica, 2014, 35(6): 1473-1486 (in Chinese). [3] WOLFIG R, JAKOVLJEVIC M. Distributed IMA and DO-297: Architectural, communication and certification attributes[C]∥Proceedings Digital Avionics Systems Conference. Piscataway, NJ: IEEE Press, 2008:1.E.4-1-1.E.4-10. [4] 蒲小勃. 現(xiàn)代航空電子系統(tǒng)與綜合[M]. 北京: 航空工業(yè)出版社, 2013: 70-86. PU X B. Modern avionics system and integration [M]. Beijing: Aviation Industry Press, 2013:70-86 (in Chinese). [5] DARPA M T O. Another big shrink: Tiling chiplets into next-generation microsystems[EB/OL]. (2016-07-19)[2017-07-05].http:∥www.darpa.mil/news-events/2016-07-19. [6] E2V. E2V and Adeneo partner to create the world’s smallest, multicore computer for aerospace applications[EB/OL]. (2016-07-18)[2017-07-05].https:∥www.e2v.com/news/e2v-and-adeneo-partner-to-create-the-worlds-smallest-multicore-computer-for-aerospace-applications/. [7] 林闖, 賈子驍, 孟坤. 自適應的未來網(wǎng)絡體系架構[J]. 計算機學報, 2012, 35(6): 1077-1093. LIN C, JIA Z X, MENG K. Research on adaptive future internet architecture[J]. Chinese Journal of Computer,2012, 35(6): 1077-1093 (in Chinese). [8] HIERGEIST S, HOLZAPFEL F. Fault-tolerant FCC Architecture for future UAV systems based on COTS SoC[C]∥Proceedings Architecture of Computing Systems. Berlin: Springer International Publishing, 2016: 1-5. [9] SCHECKEL T. Serial RapidlO: Benefiting system interconnects[C]∥Proceedings SOC Conference. Piscataway,NJ: IEEE Press, 2005: 317-318. [10] LEENS F. An introduction to I 2 C and SPI protocols[J]. IEEE Instrumentation & Measurement Magazine, 2009, 12(1): 8-13. [11] DURRIEU G, FOHLER G, GALA G, et al. DREAMS about reconfiguration and adaptation in avionics[C]∥Proceedings Embedded Real Time Software and Systems. Toulouse: European Congress Press. 2016: 48-57. [12] OLIVER R S, CRACIUNAS S S. Hierarchical scheduling over off- and on-chip deterministic networks[J]. Acm Sigbed Review, 2016, 13(4): 14-19. [13] OBERMAISSER R, EL SALLOUM C, HUBER B, et al. The time-triggered system-on-a-chip architecture[C]∥Proceedings IEEE International Symposium on Industrial Electronics. Piscataway,NJ: IEEE Press, 2008:1941-1947. [14] WASICEK A, EI-SALLOUM C, KOPETZ H. A system-on-a-chip platform for mixed-criticality applications[C]∥Proceedings IEEE International Symposium on Object/Component/Service-Oriented Real-Time Distributed Computing. Piscataway, NJ: IEEE Press, 2010: 210-216. [15] SCHOEBERL M. A time-triggered network-on-chip[C]∥Proceedings International Conference on Field Programmable Logic and Applications. Piscataway,NJ: IEEE Press, 2007: 377-382. [16] STEINER W. An evaluation of SMT-based schedule synthesis for time-triggered multi-hop networks[C]∥Pro-ceedings Real-Time Systems Symposium. Piscataway, NJ: IEEE Press, 2011: 375-384. [17] POZO PéREZ F M, RODRIGUEZ NAVAS G, HANSSON H, et al. Schedule synthesis for next generation time-triggered networks[C]∥IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA).Piscataway, NJ: IEEE Press, 2015: 1-8. [18] CRACIUNAS S S, OLIVER R S. SMT-based task- and network-level static schedule generation for time-triggered networked systems[C]∥Proceedings International Conference on Real-Time Networks and Systems. Versailles: RTNS Press, 2014: 45-54. [19] HU M, LUO J, WANG Y, et al. Scheduling periodic task graphs for safety-critical time-triggered avionic systems[J]. IEEE Transactions on Aerospace & Electronic Systems, 2015, 51(3): 2294-2304. [20] CHEN J, DU C, XIE F, et al. Schedulability analysis of non-preemptive strictly periodic tasks in multi-core real-time systems[J]. Real-Time Systems, 2016, 52(3):239-271. [21] 陳進朝, 杜承烈. 單處理器平臺下的嚴格周期任務可調度性判定[J]. 計算機工程, 2016, 42(5): 288-291. CHEN J C, DU C L. Schedulability test for strictly periodic tasks in uniprocessor systems[J]. Computer Engineering, 2016, 42(5): 288-291 (in Chinese). [22] TTE-COM. TTE-COM A653 for VxWorks 653 2.4 [EB/OL]. (2016-10-25)[2017-07-05]. Vienna, Austria:TTTech Computertechnik AG, 2016.https:∥www.tttech.com/products/aerospace/development-test-vv/middleware/tte-com-a653-for-vxworks-653/. [23] SAE. Time-triggered Ethernet: AS6802[S]. Warrendale, PA: SAE International, 2011. [24] DING S, YIN X, XU H, et al. A hybrid GA-based scheduling method for static segment in FlexRay systems[C]∥Proceedings Control and Decision Conference. Piscataway, NJ: IEEE Press, 2010: 1548-1552. [25] 代真, 何鋒, 張宇靜, 等.AFDX虛擬鏈路路徑實時尋優(yōu)算法[J]. 航空學報, 2015, 36(6): 1924-1932. DAI Z, HE F, ZHANG Y J, et al. Real-time path optimization algorithm of AFDX virtual link[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6):1924-1932 (in Chinese). [26] DUTERTRE B. Yices 2.2[C]∥Proceedings International Conference on Computer Aided Verification. Berlin: Springer International Publishing, 2014: 737-744.
2.2 發(fā)送時間偏移量的確定
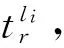
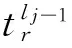


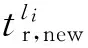
3 案例研究
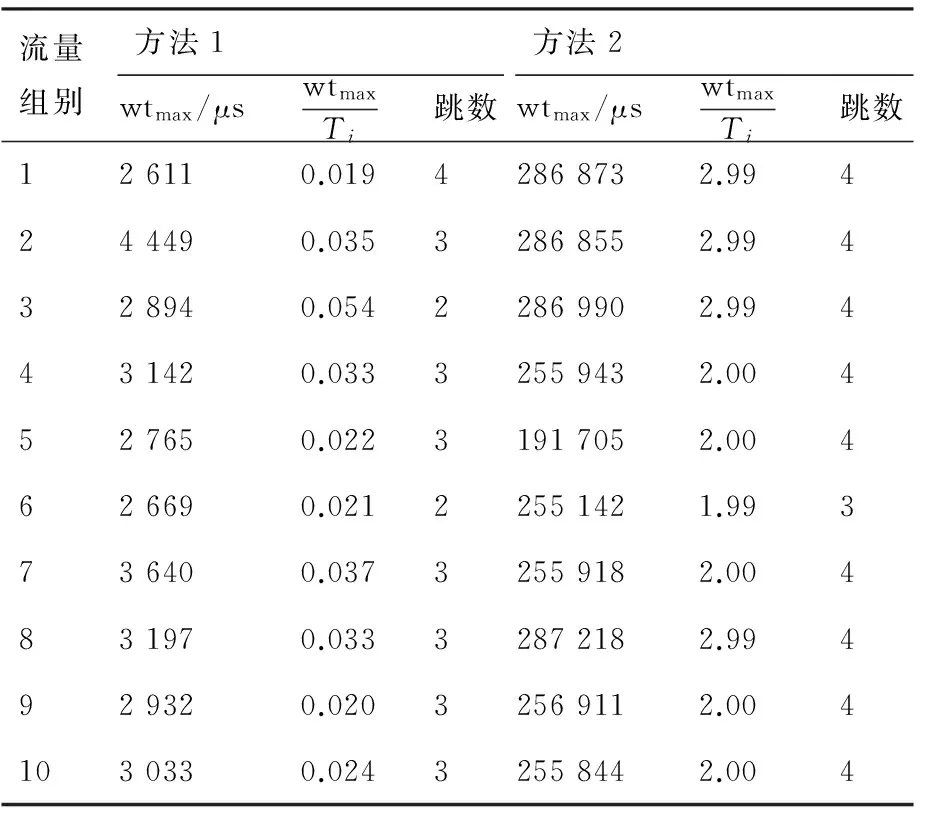
3.1 片間綜合化互連模型仿真

3.2 等待時間仿真結果對比
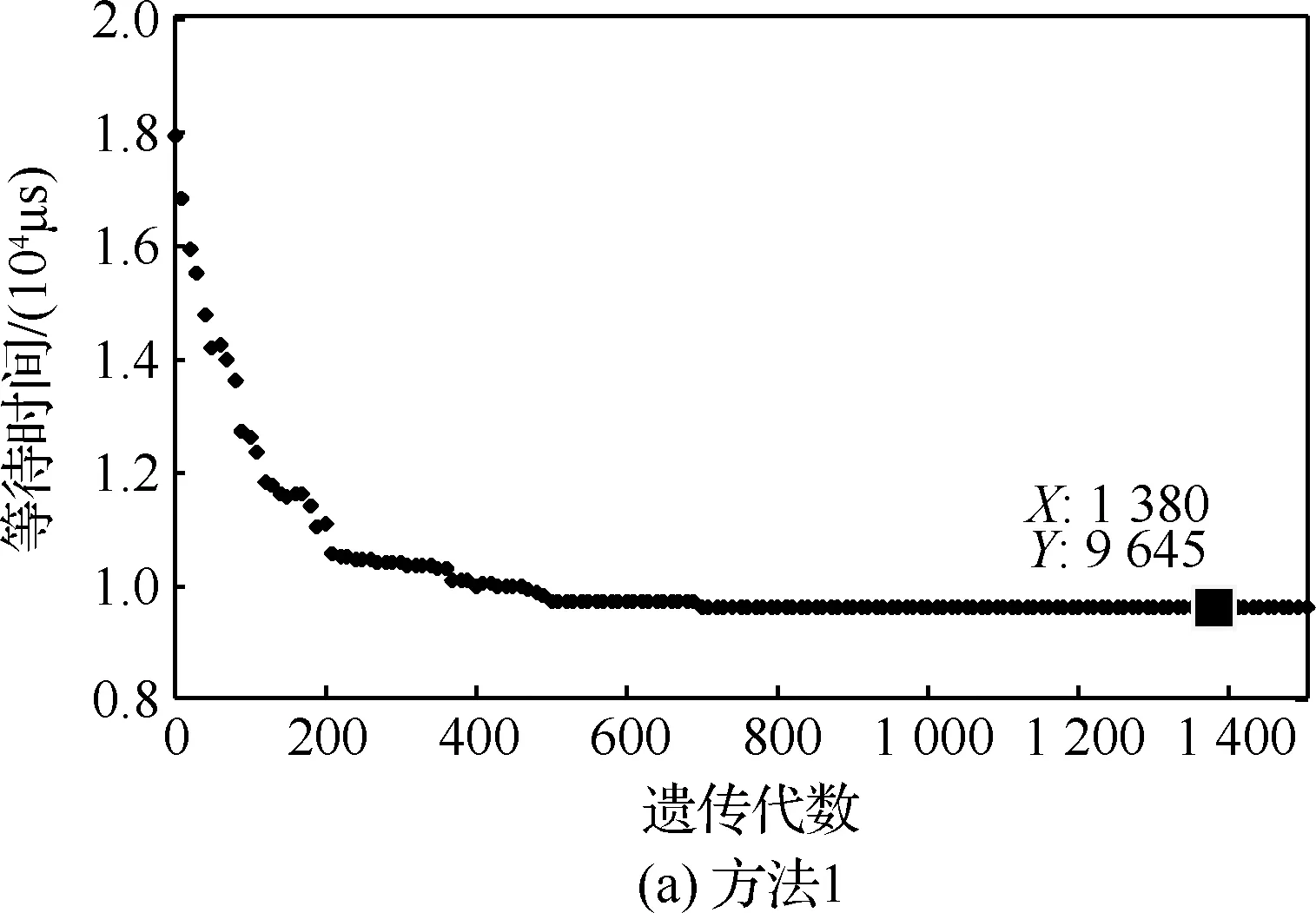
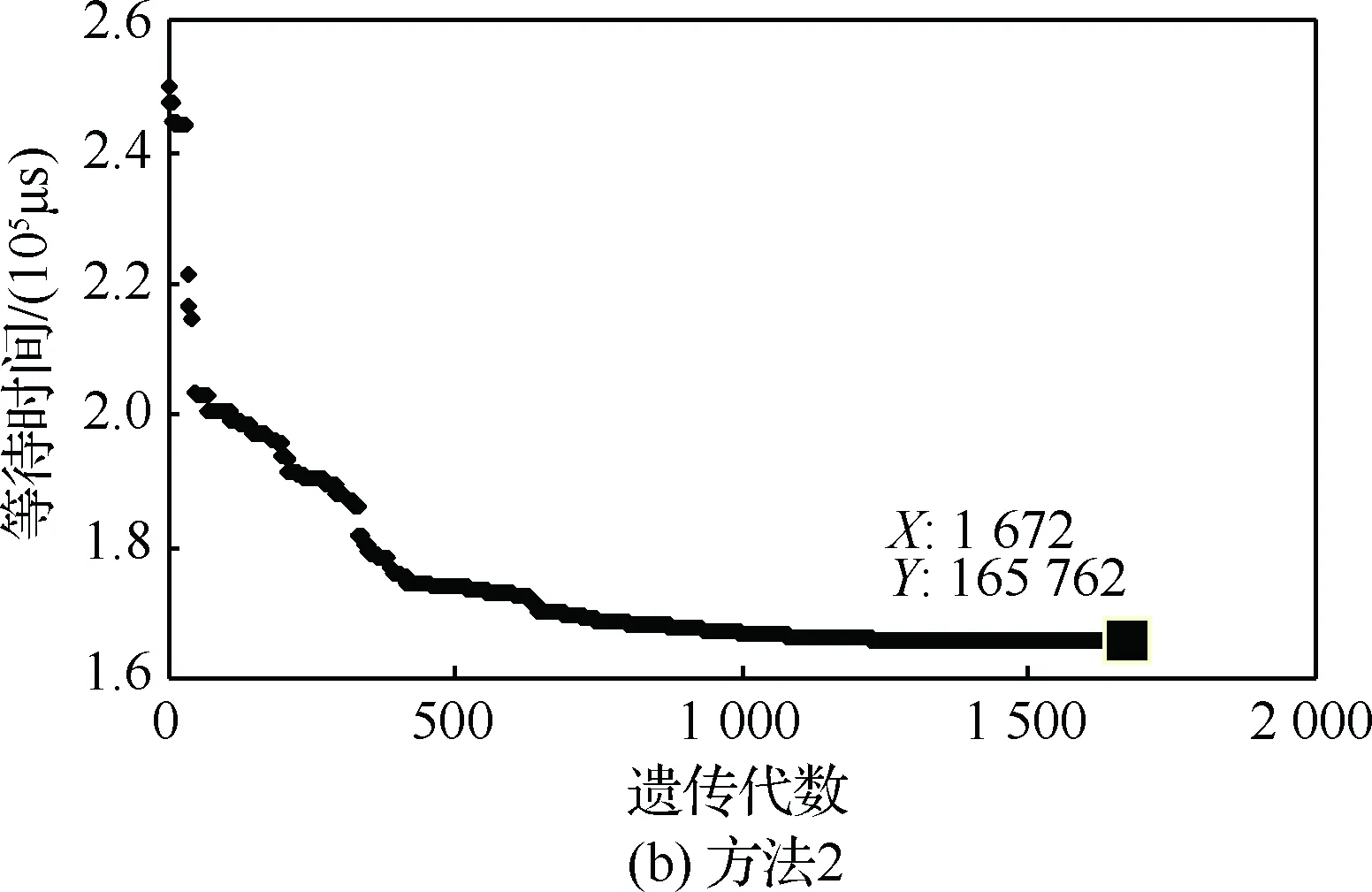
3.3 遺傳算法優(yōu)化實驗
4 結 論

