基于蒙特卡洛模擬的源網非同調的電網簡化方法

張雙梅,王國城,劉瑞超(.國網天津市電力公司 寶坻供電分公司，天津 30800；.光大生物能源(天津薊縣)有限公司，天津 30907)

0 引 言

電力系統源網間的協同調控問題是電力系統安全、經濟、可靠運行的核心問題。然而，由于系統運行的不均勻性[1-2]，導致了源網非同調現象的產生，該現象是指網的安全制約了最經濟源的運行，使部分網不隨源而變化或變化趨勢相反的現象。隨著電力系統的發展，風、光、儲等可再生能源以分散或集中的方式大規模的并入電網，源的類型、網的規模空前龐大和復雜，導致該現象將進一步加劇。

與此同時，等值簡化對異常復雜的電力系統顯得尤為必要[3-4]，簡單且精確的模型可以極大地提高系統的計算效率。近年來，國內外專家學者對此展開了大量的研究[5-6]，在動態等值中，同調機群識別、電動機、發電機、原動機等參數簡化一直是研究的熱點。靜態等值中的系統結構分區、網絡等值簡化等方面也出現了大量的研究成果[7-8]。但這些方法或僅對某一特定元件參數或僅對系統網絡結構展開研究，沒有考慮源網間的非同調關系，且簡化后的等效模型存在依賴于運行點、網絡潮流模式變化較大等問題[9-10]。

針對上述情況，本研究提出源網同調和非同調的指標、判別源網同調的方式，以及利用源網同調特點實現電網分類簡化的方法。

1 源網非同調現象

根據功率分布理論，電網中任意支路中的潮流為具有不同系數的電源提供的功率分量的代數和，功率分量的歸屬電源明確，體現了源網之間的耦合關系。然而，對應負荷曲線中某點，電源最經濟運行方式受網的制約而出現非同調的現象。本研究采用三節點系統對此情況進行說明，如圖1所示。

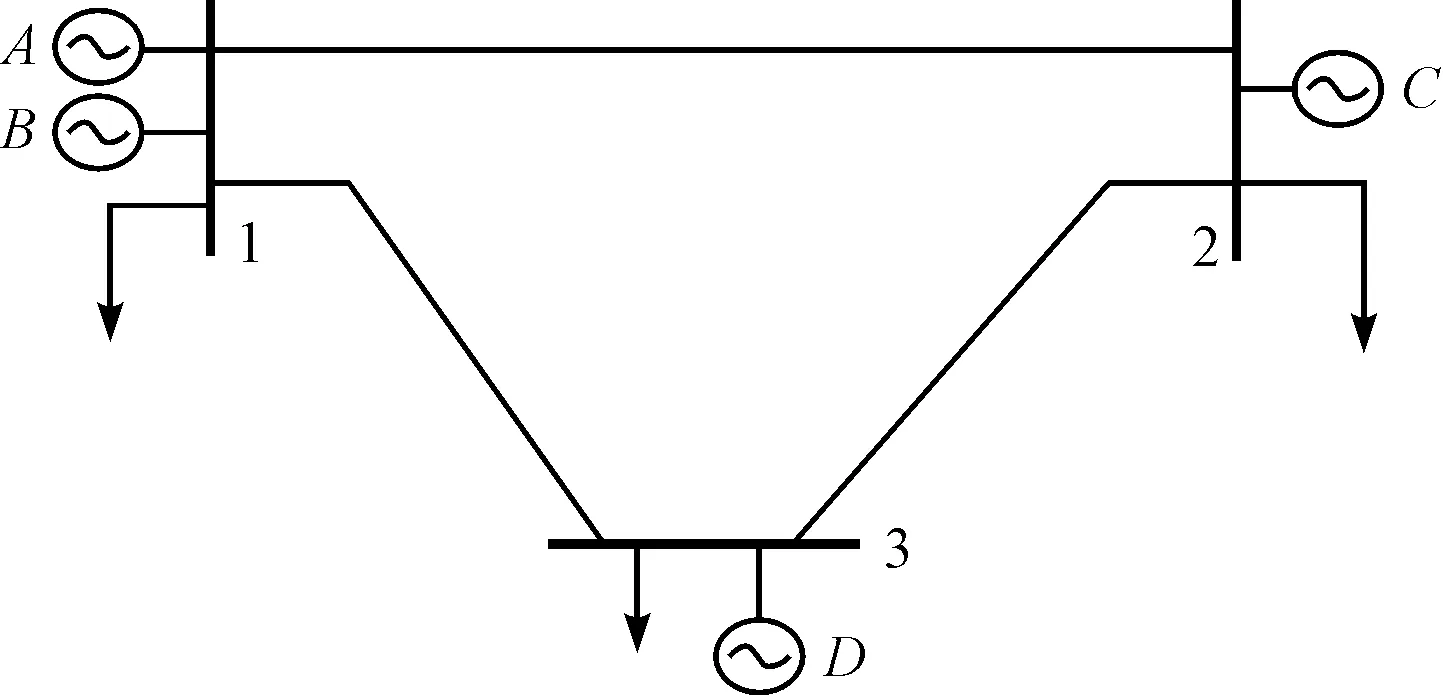
圖1 三節點系統

系統負荷運行模式如表1所示。

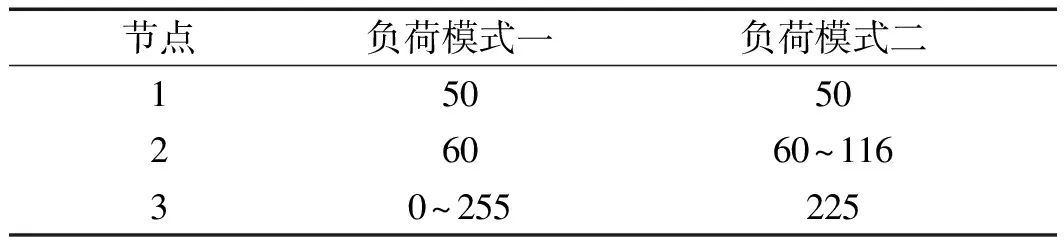
表1 負荷運行模式(單位：MW)

1.1 源網同調

在負荷模式一情況下，對其進行連續潮流計算，得到系統各電源及網絡潮流變化情況如表2所示。負荷最大時系統運行如圖2所示。此時恰好滿足網的制約(支路1-2達輸電限值)。

結果顯示，在該負荷模式下，隨著負荷的增加，源網保持同步增加，源的最經濟運行方式不受網的制約，源網同調。

表2 負荷模式一下系統有功變化情況(單位：MW)

1.2 源網非同調

在負荷模式二下，節點1、節點3處的負荷保持不變，節點2處的負荷由60 MW增長至116 MW，對其進行連續潮流計算，可得系統各電源及網絡潮流變化情況如表3所示。

負荷最大時系統運行如圖3所示。

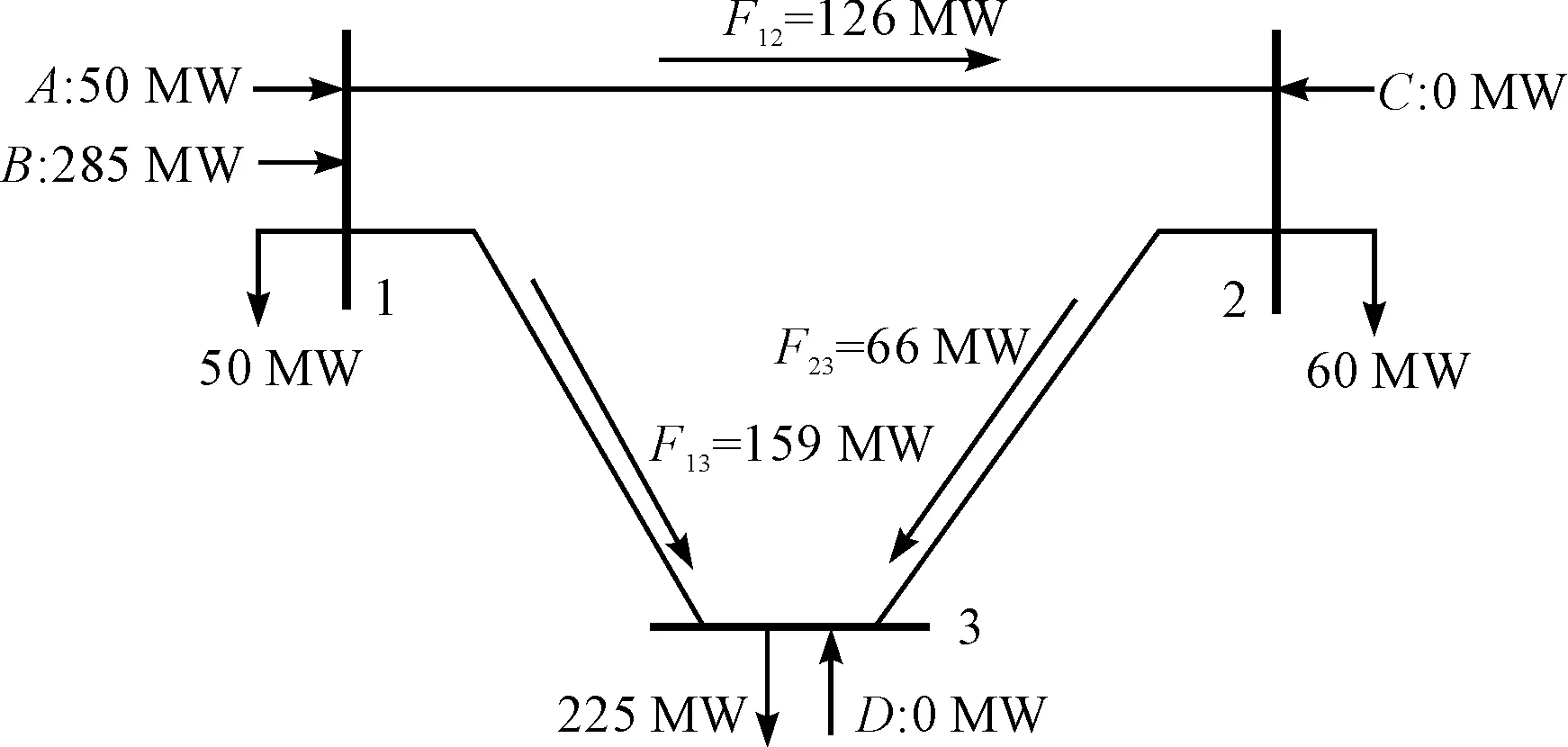
圖2 負荷模式一最值時系統運行

負荷1負荷2負荷3電源A電源B電源C電源D支路1-2潮流支路1-3潮流支路2-3潮流初值5060225502850012615966終值501162252228508412613110

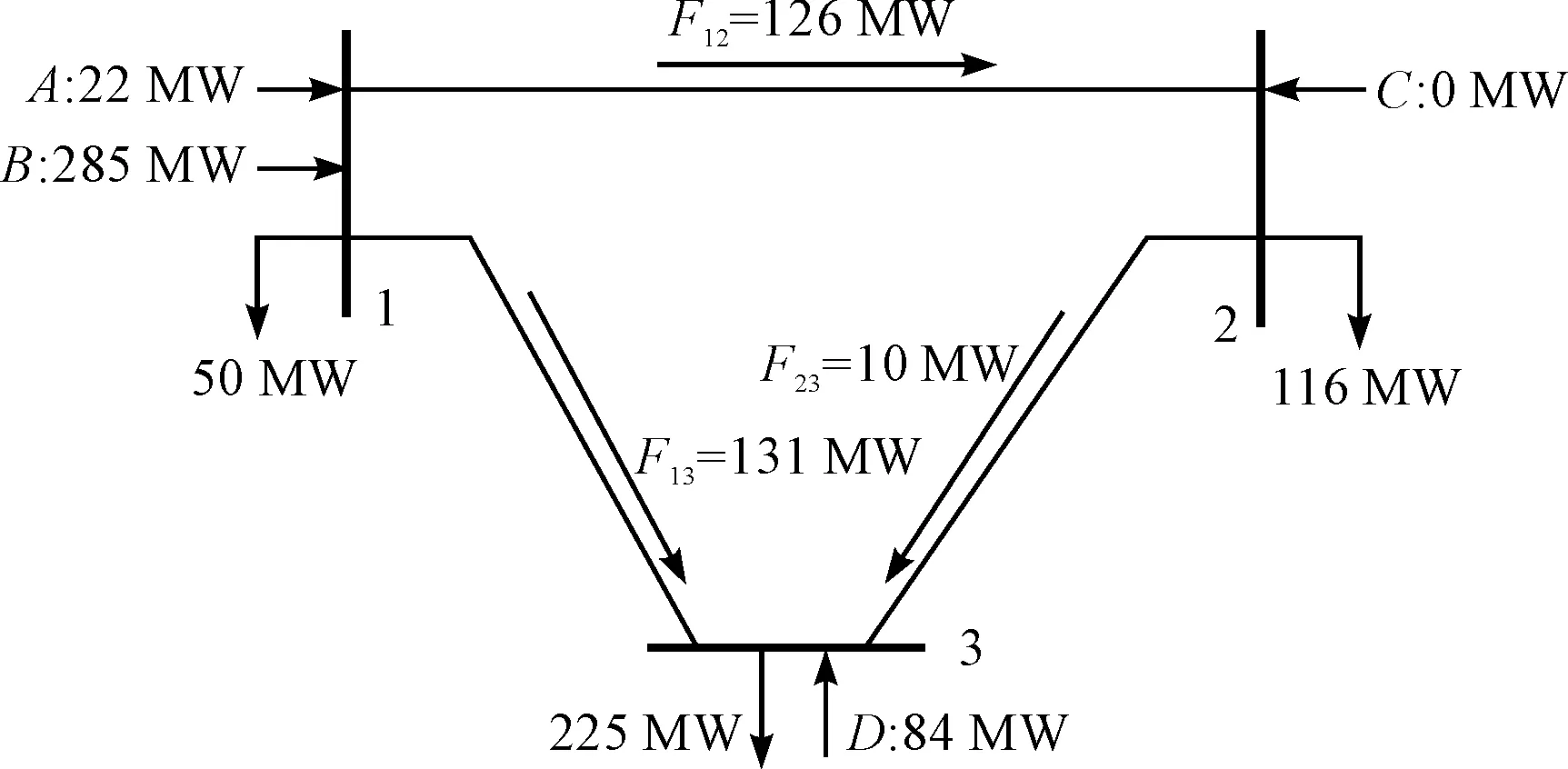
圖3 負荷模式二最值時系統運行

此時，隨著節點2負荷增大，受網的制約，電源A、支路1-3、支路2-3有功減小，電源D有功增大，支路1-2有功保持不變，網不隨電源D同調變化。

2 源網非同調識別指標

與源網非同調相反，同調的源和網指的是源網有功變化同步增大或減小，表現了源網內部無制約和擠兌，可分為一類，顯示源的屬性；而部分網在源的變化過程中保持不變，相對獨立，也可分為一類，顯示網的特性；若同調源與其互聯的網非同調，則網將其分為獨立的類。經過此劃分，原電力系統可簡化為由同類的源與網組成的簡化系統。

同調屬性是一個動態變化識別的過程，設當前時刻為t0，定義超前時刻t1時，源網非同調的識別指標為：

(1)

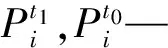
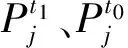
3 蒙特卡洛模擬及源網分類識別

3.1 蒙特卡洛模擬系統運行

在不同時刻電力系統的負荷可能不同，服從隨機變化規律，而蒙特卡羅模擬預測法[11]是一種利用隨機數來解決具有動態隨機性質問題的方法，在電力系統分析中已得到廣泛應用[12]。

假設系統的發電、負荷服從區間內的均勻分布，即：

(2)

(3)

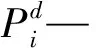
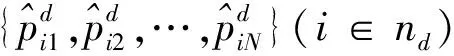
(4)

(5)

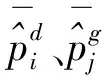
3.2 源網同調狀態識別

根據潮流計算結果，設t1時刻得到的系統源網功率分別為：

(6)

式中：n—系統節點數；b—支路數。

設t0時刻系統潮流分布已知，表示為：

(7)

則t1時刻相對于t0時刻源和支路的有功變化量分別為：

(8)

其中:

(9)

(10)

根據式(8)的數據，使用(1)的識別指標可識別出系統的同調源和同調網，進一步對式(8)進行計算，可得到識別源網同調的矩陣：

C=(ΔP)T?(ΔPl)′

(11)

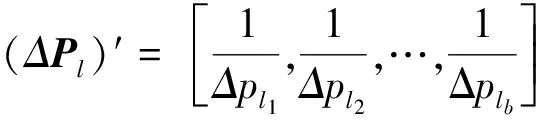
在上述計算過程中，存在部分源節點保持不變的情況，這部分節點為聯絡性節點，可根據系統結構將其分類。

4 實驗及結果分析

筆者采用IEEE118進行仿真，以驗證本研究的算法，系統結構參數參考文獻[13]。

經過本研究第1及第2部分分類算法，將系統分為3類的距離比分為兩類的小，所以將系統分為3類為最優的分類，分為3類的結果如表4、圖4所示。

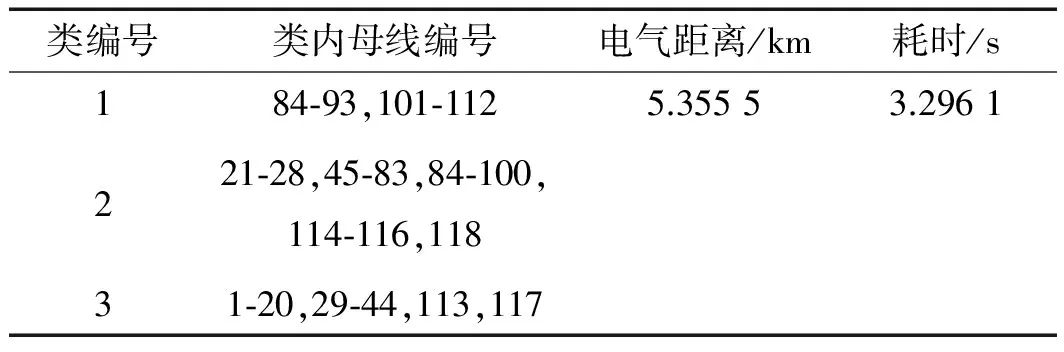
表4 IEEE118母線系統分為3類結果

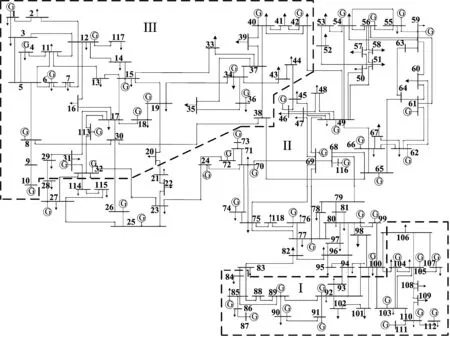
圖4 IEEE118母線系統分為三類示意圖

按圖4所示的分類結果將系統簡化為如圖5所示的三母線系統。

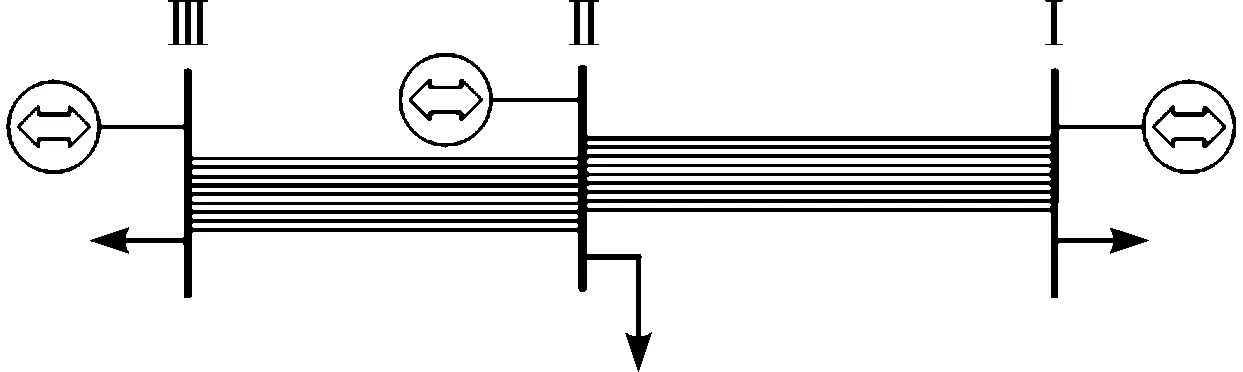
圖5 IEEE118母線系統簡化為三母線系統示意圖

其中，母線Ⅰ與Ⅱ之間有83-84、83-85、94-93、94-92、100-92、100-101、100-103、100-104、100-106共9條并行支路，母線Ⅱ與Ⅲ之間有21-20、23-32、26-30、27-32、28-29、49-42、45-44、65-38、114-31共9條并行支路。

根據文獻[14]算法計算圖8所示簡化電網PTDF矩陣Hr及節點有功注入Pr分別為：

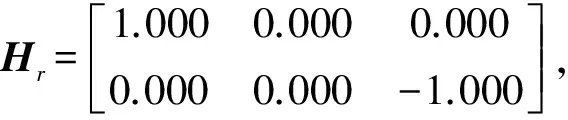
筆者使用本文所提方法對圖5所示簡化系統進行潮流計算，與文獻[14]的比較結果如表5所示。

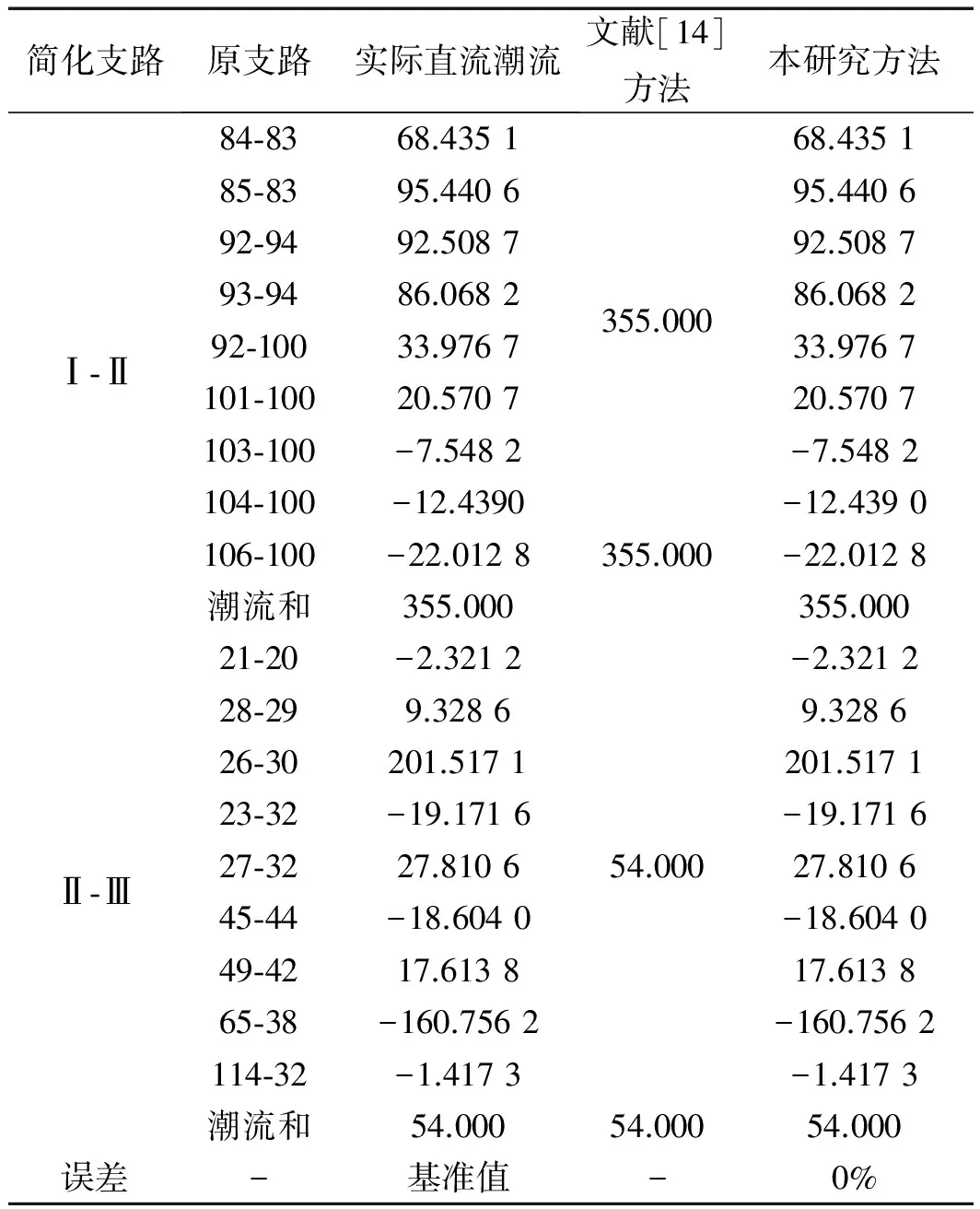
表5 簡化IEEE118母線系統潮流結果比較/MW

5 結束語

本研究根據電網各個電源具有同調的特點提出了一種新的電網簡化方法。通過使用本研究所提方法，在算例部分可以看出，可以極大簡化電網的分析和調度，有助于提高電網監視的效率，且可以達到與原始電網相同的調度結果。

[1] AAR K B, ALLXLLED S S, MUSTAFA M W, et al. A novel method for ATC computations in a large scale power system[J].IEEETrans.OnPowerSystems,2004,19(2):1150-1158.

[2] OU Y, SINGH C. Assessment of available transfer capability and margins[J].IEEETrans.Onpowersystems,2002,17(2):463-468.

[3] ANNAKKAGE U D, NAIR N K C, LIANG Y, et al. Dynamic system equivalents: a survey of available techniques[J].IEEETransactionsonPowerDelivery，2012，27(1)：411-420.

[4] GHASSEMI F, KOO K L. Equivalent network for wind farm harmonic assessments[J].IEEETransactionsonPowerDelivery，2010，25(3)：1808-1815.

[5] 劉寶英，楊仁剛.采用輔助問題原理的多分區并行無功優化算法[J].中國電機工程學報，2009，29(7)：47-51.

[6] 顏 偉,何 寧.基于Ward等值的分布式潮流計算[J].重慶大學學報:自然科學版,2006,29(11):36-40.

[7] LIANG Min. Total transfer capability computation for multi-area power systems[J].IEEETransactionsonPowerSystems,2006,21(3):1141-1147.

[8] 劉志文，劉明波.基于Ward等值的多區域無功優化分解協調算法[J].電力系統自動化，2010，34(14)：63-69.

[9] 蘇勛文，米增強，王 毅.風電場常用等值方法的適用性及其改進研究[J].電網技術，2010，34(6)：175-180.

[10] XV Jian-zhong, GOLE A M, ZHAO Cheng-yong. The use of averaged-value model of modular multilevel converter in DC grid[J].IEEETransactionsonPowerDelivery，2015，30(2)：519-528.

[11] JI Y H, JUNG D Y, KIM J G, et al. A real maximum power point tracking method for mismatching compensation in PV array under partially shaded conditions[J].IEEETransactionsonPowerElectronics,2011,26(4):1001-1009.

[12] PATEL H, AGARWAL V. Matlab-based modeling to study the effects of partial shading on PV array characteristics[J].IEEETransactionsEnergyConversion,2008,23(1):302-310.

[13] 王錫凡，肖云鵬，王秀麗.新形勢下電力系統供需互動問題研究及分析[J].中國電機工程學報，2014，34(29)：5018-5028.

[14] HYUNGSEON O. A new network reduction methodology for power system planning studies[J].IEEETrans.onPowerSystems,2010,25(2):677-684.