軟酉空間及其運算性質

劉用麟，吳成達

（武夷學院 數學與計算機學院， 福建 武夷山 354300）

由于客觀世界中或客觀世界在向人腦反映的過程中存在著大量的不精確、不完全或不完全可靠的信息（統稱為不確定信息）,因而，在現實社會中需要處理大量的不確定性信息，經典的數學方法不能有效地處理.目前有一些理論，如概率理論，模糊集理論和粗糙集理論被用來處理不確定性事物，但這些理論都有自己的困難和問題.Molodtsov[1]認為原因之一可能是這些理論的參數工具不足.為了克服這些困難，1999年Molodtsov引進了軟集的概念作為一種新的處理不確定性的數學工具，他同時指出了軟集的若干可能應用方向.軟集理論提出后，經過一些學者的擴展研究，取得了較大進展.Maji等[2]應用軟集理論于決策分析，Maji等[3]還研究了軟集理論的運算.隨后,Ali等[4]指出了文[3]中所提出的交、并運算的一些問題,并給出了新的運算.Chen等[5]提出了參數約簡的一個新定義，并將這個定義與粗糙集理論中相關概念屬性約簡的進行了比較.近年來，Aktas等[6]定義了軟群并給出了相關的性質，將軟集理論應用到群結構上去.從此，一些學者成功地將軟集合理論應用到各類代數系統上,如Feng等[7]提出了軟半環，Zhan等[8]提出了軟BL代數，Acar等[9]提出了軟環，Akram等[10-11]提出了軟李代數、軟K-代數等概念.本文作者也對軟代數理論作了一些研究，提出了軟剩余格、軟結合BCI-代數等[12-14]。已經證明軟代數具有與經典代數不一樣的性質。

本文將軟集合理論應用到酉空間中.首先給出酉空間和軟集合理論的相關知識;再對軟酉空間進行了合理的定義,給出具體的例子來證明軟酉空間的存在性;接著研究軟酉空間的運算性質,給出軟酉空間的擴展交、限制交和限制差分;最后研究軟酉空間的同態性質。

1 預備知識

1.1 歐幾里得空間的定義及性質

定義1.1.1[15]令V是實數域R上一線性空間,在V上定義一個二元實函數,稱為內積,記成（α,β）,它具有以下性質：

1、（α,β）=（β,α）;

2、（kα,β）=k（α,β）;

3、（α+β，γ）=（α，γ）+（β，γ）;

4、（α，α）≥0,當且僅當 α=0 時（α，α）=0.

這里α，β，γ是V中任意向量,k是任意實數，稱這樣的線性空間V為歐幾里得空間。

定理1.1.1[15]若V1,V2是歐式空間V的兩個子空間,那么它們的交V1∩V1也是V的子空間.

1.2 酉空間的定義及性質

歐式空間是專門對實數域上的線性空間而討論的,因此,酉空間就是一種歐式空間.

定義1.2.1[15]設V是復數域上的線性空間,在V上定義了一個二元復函數,稱作內積,記成（α,β）,它具有以下性質：

2、（kα,β）=k（α,β）;

3、（α+β，γ）=（α，γ）+（β，γ）;

4、（α，α）是非負實數,且（α，α）=0 當且僅當 α=0.這里α,β，γ是γ中任意向量,k是任意復數,這樣的線性空間V稱為酉空間.

性質1.2.1[15]由內積的定義可得到以下性質：

2、（α，β+γ）=（α，β）+（α，γ）;

4、向量 α，β,當（α，β）=0 時稱為正交或互相垂直.

定義1.2.2[15]設W是酉空間V的一個非空子集,若對于V中的加法及復數域C與V的純量乘法構成復數域C上的一個線性空間,則稱W為V的酉子空間.

1.3 軟集合理論相關定義與基本運算

定義1.3.1[1]設U是一個論域,E是參數集,U?E,P（U)是 U 的冪集.若 F 是 A 到P（U)的映射,則稱（F,A）為U上的一個軟集合.

定義1.3.2[4]設U的兩個軟集合分別是（F，A）和（G,B）,定義為（H,C）這兩個軟集合的擴展交,此時 C=A∪B,則

記為（F,A）∩E（G,B）=（H,C）.

定義1.3.3[4]設U的兩個軟集合分別是（F,A）和（G,B）,A∩B≠φ

1、此時可對這兩個軟集合的限制交定義為軟集合（H,C）,即：C=A∩B,?e∈C，H（e）=F（e）∩G（e）記為（F,A）∩△（G,B）=（H,C）

2、此時可對這兩個軟集合的限制并定義為軟集合（H,C）,即 C=A∩B,?e∈C，H（e）=F（e）∩G（e）.記為（F,A）∩R（G,B）=（H,C）

3、此時可對這兩個軟集合的限制差定義為軟集合（H,C）,即 C=A ∩B,?e∈C，H（e）=F（e）G（e）,記為（F,A）∩D（G,B）=（H,C）

定義1.3.4[4]設U的兩個軟集合分別是（F,A）和（G,B）,若滿足以下條件

1、A?B；

2、?x∈A，F（x）?H（x）.

則稱（F,A）為（G,B）的軟子集，記作（F,A）?（G,B）.

2 軟酉空間

2.1 軟酉空間的定義

為了便于說明,在這里令V是一個酉空間,A是一個非空集合.

定義2.1.1 設（F,A）是酉空間V上的一個軟集合,若?x∈A，F（x）,是 V 上的一個酉子空間,則稱（F,A）為V上的軟酉空間.

推論2.1.1 設（F,A）和（G，B）是酉空間上的兩個軟酉空間,如果滿足下列兩個條件：

1、B?A;

2、?x∈B，G（x）?F（x）.

則稱（G,B）是（F,A）的軟酉子空間,記為（F,A）?（G,B）.

定義2.1.2 設（F,A）和（G,B）是 V 上的兩個軟酉空間,當 G=F 時,僅需滿足條件：B?A,則（G,B）是（F,A）的軟酉子空間.

2.2 軟酉空間的例子

例2.2.1 在線性空間 Cn中,對于向量 α=（α1，α2，…，αn）,β=（b1，b2，…，bn）,定義內積,則Cn就成為一個酉空間.取S=,易證 S 是 Cn的酉子空間.令 A=｛0,1｝,定義

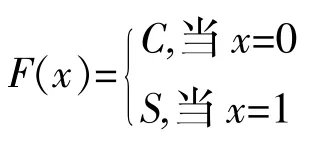
則（F,A）為 Cn上的軟集合.又 F（0）=Cn,F（1）=S皆是 Cn的酉子空間,所以（F,A）為Cn上的軟酉空間.

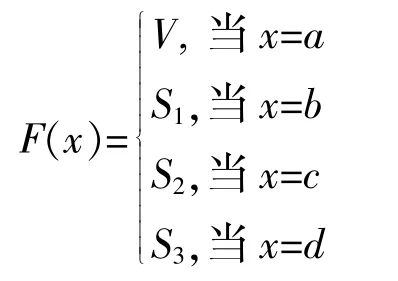
于是 F（a）=V，F（b）=S1，F（c）=S2，F（d）=S3， 都是 V 的酉子空間，所以（F，A）為｝上的軟酉空間.

3 軟酉空間的性質

3.1 軟酉空間的擴展交

引理3.1.1 若A,B均為酉空間X的酉子空間,則A∩B也是X的酉子空間.

證明：首先,根據0∈A,0∈B可知 0∈A∩B,因此A∩B 是非空的.其次,若 α,β∈A∩B,即 α,β∈A,且 α,β∈B,則 α+β∈A,α+β∈B,于是 α+β∈A∩B.對 α∈A∩B,K∈C,即 α∈A,α,∈B,那么 kα∈A,kα∈B,因此 kα∈A∩B,所以A∩B也是X的酉子空間.

定理3.1.1 如果（F1，A1）和（F2，A2）是酉空間 X 上的兩個軟酉空間,則（F1，A1）∩E（F2，A2）也是酉空間 X上的軟酉空間.

證明：令（F，A）=（F1，A1）∩E（F2，A2）,其中 A=A1∪A2，?x∈A

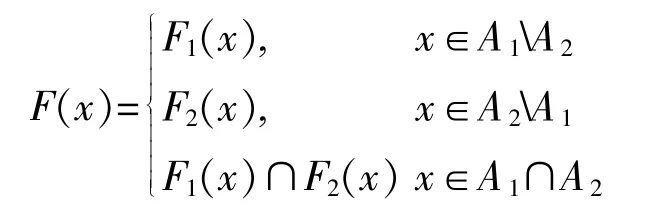
因為（F1，A1）和（F2，A2）都是酉空間 X 上的軟酉空間,對?x∈A,則x∈A1A2或 x∈A2A1或 x∈A1∩A2三者必然成立一個,若 x∈A2A1或 x∈A1A2則 F（x）=F1（x）或 F2（x）,均為 X 的酉子空間. 若 x∈A1∩A2,則 F（x）=F1（x）∩F2（x）,由引理 3.1.1,F（x）也為 X 的酉子空間.因此是（F，A）是X上的軟酉空間.

3.2 軟酉空間的限制交

定理3.2.1 如果（F1，A1）和（F2，A2）都是酉空間 X上的軟酉空間,且 A1∩A2≠φ,則（F1，A1）∩△（F2，A2）也是X上的軟酉空間.

證明：令（F，A）=（F1，A1）∩△（F2，A2）,其中 A=A1∩A2且對?x∈A，F（x）=F1（x）∩F2（x）. 由于（F1，A1）和（F2，A2）都是 X 上的軟酉空間,所以對?x∈A1,有 F1（x）是 X 上的酉子空間;同理可得,?x∈A2,有 F2（x）是 X上的酉子空間,因此,對?x∈A,有F（x）是 X 上的酉子空間,從而（F1，A1）∩△（F2，A2）是 X 上的軟酉空間.

3.3 軟酉空間的限制差分

定理3.3.1 如果（F1，A1）和（F2，A2）都是酉空間 X上的軟酉空間,且 A1∩A2≠φ,則（F1，A1）∩D（F2，A2）一定不是酉空間X上的軟酉空間.

證明：令（F，A）=（F1，A1）∩D（F2，A2）,其中 A=A1∩A2且對?x∈A，F（x）=F1（x）F2（x）.由已知,對?x∈A,F1（x），F2（x）為酉空間 X 的酉子空間,所以 0∈F1（x）,0∈F2（x）,故 0?F（x）.于是，F（x）不是酉空間 X 上的酉子空間,故（F1，A1）∩D（F2，A2）一定不是酉空間 X 上的軟酉空間.

3.4 軟酉空間的同態性質

定義3.4.1 設X和Y是復數域C上兩個酉空間,f：A→B是一個映射,若滿足：

1、?α,β∈A,有 f（α+β）=f（α）+f（β）,

2、?k∈C，α∈A,有 f（kα）=kf（α）,

則稱f是酉空間A到B的一個同態映射.若f是滿射,則稱f是酉空間A到B的一個滿同態；若f是單射,則稱f是酉空間A到B的一個單同態；若f是雙射,稱f是酉空間A到B的一個同構.

引理3.4.1 設X,Y是兩個酉空間,如果f：X→Y為從X到Y的酉空間同態：

1、假設X的酉子空間為M,那么Y的酉子空間就是 f（M）.

2、假設Y的酉子空間為L,那么的酉子空間就是f-1（L）.

證明：設?y1，y2∈f（M）,在 M 中存在兩個元素 x1,x2,使得 y1=f（x1）,y2=f（x2）.則 y1+y2=f（x1）+f（x2）=f（x1+x2）由M為X的酉子空間可知x1+x2∈M,從而y1+y2=f（x1+x2）∈f（M）；設?k∈C,?y∈f（M）,則 M 中存在 x,使得 y=f（x1）,于是 ky=kf（x）=f（kx）,由于 kx∈M,所以ky=f（kx）∈f（M）.因此 f（M）為 Y 的酉子空間.同理可證,f-1（L）為X 的酉子空間.

定理3.4.1 設X,Y是兩個酉空間,如果f：X→Y為從X到Y的酉空間同態,（F，A）是上的軟酉空間,則（f（F），A）是 Y 上的軟酉空間.

證明：首先由（f（F），A）的定義知（f（F），A）為 Y 上的軟集.由（F，A）是X上的軟酉空間知,對任意的α∈A,F（α）是 X 的酉子空間,由引理 3.4.1,可知 f（F（α））為 Y的酉子空間,即對任意的 α∈A，f（F）（α）是 Y 的酉子空間,從而有（f（F），A）是 Y 上的軟酉空間.

定理3.4.2 設X,Y是兩個酉空間,如果f：X→Y為從X到Y的酉空間同態,（H,B）是Y上的軟酉空間,則（f-1（H），B）為 X 上的軟酉空間.

證明：首先由（f-1（H），B）的定義知（f-1（H），B）為 X上的軟集.對任意的b∈B,由（H,B）是Y上的軟酉空間知 H（b）是 Y 的酉子空間,因此由引理 3.4.1,f-1（H（b））是 X 的酉子空間,即對任意的 b∈B,f-1（H）（b）是 X 的酉子空間,從而有（f-1（H），B）為 X 上的軟酉空間.

定理3.4.3 如果 f：X→Y 是一個酉空間同態,（F，A）和（H,B）是酉空間 X 上的軟酉空間,（F，A）?（H,B）,則（f（F），A）?（f（H），B）.

證明：由（F，A）?（H,B）可知 A?B,故對?x∈A,有F（x）是 H（x）的酉子空間.又由 f是同態映射,有 f（F）（x）=f（F（x））是 f（H（x））=f（H）（x）的酉子空間,由定理3.4.1 可知（f（F），A）與（f（H），B）為 Y 上的軟酉空間,再根據定義 2.1.2 可得（f（F），A）?（f（H），B）.