基于多目標優化算法的交流電抗器參數設計
張華軍,黃 鵬,蘇義鑫
?
基于多目標優化算法的交流電抗器參數設計
張華軍,黃 鵬,蘇義鑫
(武漢理工大學自動化學院,武漢 430070)
以整流電路為應用背景,對其產生的電流諧波進行了分析,針對電壓占比法引入交流電抗器較片面的問題,引入多目標優化算法對系統輸入電流諧波畸變率、電抗器占壓比、整流輸出電壓紋波系數等方面進行針對性的優化計算,并對兩種方案進行仿真比較分析,證明了多目標優化算法的優越性。
整流電路交流 電抗器 多目標優化算法
0 引言
整流系統中含有的大量非線性電力負載,給電網帶來了大量的諧波污染[1]。我國對于諧波治理主要分為主動諧波治理和被動諧波治理。主動諧波治理從諧波源本身出發抑制諧波的產生,主要有脈沖寬度調制(PWM)技術、增加變流裝置的相數或脈沖數、采用高功率因數變流器等方法;被動諧波治理通過配置額外諧波治理裝置來實現諧波治理,主要有引用無源電力濾波器、有源電力濾波器、混合型有源電力濾波器以及統一電能質量調節器等技術來實現諧波治理[2]。對于高頻開關電源系統中的高頻諧波,以引用輸入電抗器方法效果最為顯著,工程中通常以電抗器電壓占比為研究對象對其進行選取[3],但是此方法忽略了功率因數、輸出電壓紋波、諧波畸變率等因素對系統的影響,因此無法獲得最佳電抗器電感量,影響系統的輸出性能。
針對常規整流電路中電抗器電感量設計方法不完善的問題,本文提出了一種基于多目標優化理論的電抗器電感量計算方法,以電流諧波畸變率、電抗器電壓、功率因數等為目標進行全局優化,推導了最佳電感量計算方法,并利用仿真分析檢驗了所提出的電感量計算方法的有效性。
1 輸入電抗器濾波原理
如圖1所示,La、Lb、Lc為三相輸入電抗器。開關電源的整流部分采用二極管不可控橋式整流電路,后級濾波部分采用電解電容作為濾波元件。當功率在幾千瓦到幾十千瓦的三相整流電路電源電壓發生突變時,其電壓上升率為:

這就可能導致可控整流元器件誤導通,而電感的特性是交流感抗大,直流感抗小且近似為零,所以引入交流電抗器將會使母線上的電壓波動較小,這也就起到了維持母線電壓水平的作用[4]。

式中i為各次諧波電流,其中主要以5、7、11、13次諧波為主。
輸入電流中大量的諧波電流將會使∑較大,造成交流輸入功率因數降低。采用相應的電抗器后可以使系統中的諧波電流含量降低,進而可以有效提高系統的輸入功率因數[5]。
2 電壓占比法引入輸入電抗器
輸入電抗器電感量越大,抑制電流變化的能力就越強,電流諧波畸變率會更低,整流輸出電壓紋波更小,但電感量過大的電抗器會導致電抗器分壓過大,整流輸出電壓變小,系統的動態相應速度也會明顯降低,電抗器上較大的分壓也將會導致運行過程中損耗增大,影響電抗器的使用壽命,系統的運營成本會更高,不利于整個系統的長期運行。工程上一般根據電抗器每相繞組上的壓降ΔU計算電抗器的電感量[6]:

式中:L為電抗器上流過的電流,0為電網頻率,一般為50 Hz。
壓降的選擇一般取在網側相電壓的2~4%,重載運行時以4%來計算電感值和確定線圈截面等。僅僅只考慮三相輸電線路上的電壓降雖然可以使輸出電壓相對穩定,但是對于整個系統運行來說這樣的選取方式將會顯得比較片面,運行過程中產生諧波的種類含量、功率因數、整流輸出電壓紋波系數,乃至后期選用電抗器的體積、成本等都是電抗器選用過程中不可忽視的影響。針對常規方法選取電抗器較片面的問題,本文提出了基于多目標優化算法對目標函數求取最優解的方法來選取電抗器電感量。
3 多目標優化算法
在多目標優化算法中各個子目標可能是相互沖突的,一個子目標的改善有可能引起另一個子目標性能的降低,所以只能在它們中間進行協調和折中處理,才能使各個子目標函數盡可能達到最優。法國經濟學家V.Pareto(1848-1923)最早研究了經濟學領域內的多目標優化問題并提出了Pareto解集:通常一個多目標問題大多會具有很多個Pareto最優解[7, 8]。在實際應用問題中,必須根據對問題的了解程度和決策人員的個人偏好,從Pareto最優解集合中挑選一個或一些解作為多目標優化問題的最優解。求解多目標優化問題的關鍵步驟在于求取該問題的所有最優解[9]。
3.1 基于多目標優化算法的最優解求取
本文基于加權求和法將目標函數轉換為單目標優化問題進行求解[10]。首先建立如下優化目標函數:

上式中f1(x)~fn(x)為影響電抗器選型的各子目標經過數據標準化處理后的函數,ω1~ω4為各子目標函數所對應的權重,其中
同時參數x的迭代公式為:

通過比較F(x(n+1))和F(xn)的值即可得到目標函數在xn附近的最小值,然后進行算法的反復迭代即可逐次逼近目標函數最小值,從而得到目標函數最優解。
3.2 針對電抗器電感量的多目標優化計算
本文選用380 V/50 Hz的三相工頻交流電作為輸入電源,負載為7.5 Ω的電阻,濾波電容取3000 μF,輸出電壓有效值為514.7 V;輸入電壓有效值為220 V,輸入電流有效值為55.14 A.輸入電流諧波畸變率為94.60%;電路仿真模型如圖1所示。
求取多目標優化問題的最優解時需要對數據進行標準化處理,然后才能對標準化后的數據進行多目標優化求解。其中數據標準化處理主要包括數據同趨化處理和無量綱化處理。
數據同趨化處理:

數據無量綱化處理:
式中()為預處理的數據,min()和max()分別為預處理數據中的最小值和最大值。
數據同趨化處理是為了使各個子目標對整個系統的作用方向趨于一致,再加總才能得到正確的結果,而數據無量綱化處理主要用于解決數據的可比性,將原始數據轉化成無量綱化目標測評值,使各子目標都處于同一個數量級別上,然后才能對數據進行求解[11]。
對該電路進行各個電感量的仿真后得到的數據標準化表如表1所示:

表中為電抗器電感量,i、L、b、分別為在不同電抗器電感量下輸入電流諧波畸變率、電抗器占壓比、整流輸出電壓紋波系數、輸入功率因數標準化后的函數值。
通過對數據進行擬合處理,可得到各子目標函數的函數表達式:
電流諧波畸變率函數(i):

電感電壓占比函數(UL):

輸入功率因數函數(P):
目標函數:

根據各子目標的重要程度賦予它們相應的權系數,這里選取1=0.2,2=0.5,3=0.1,4=0.2。即可得到系統的目標函數。將函數代入上述算法,并設定初始值為0=0.1mH,取用步長設為=0.001,電抗器最優解取用范圍為0.1~1mH,通過多目標優化算法的迭代可得到的最優解為0.442 mH。
而基于電壓占比法所得的電抗器電感量為:
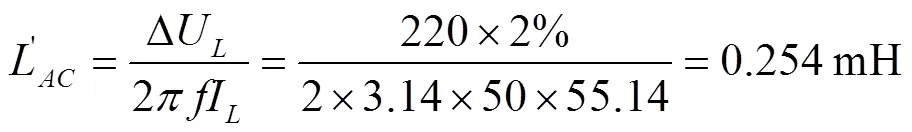
表2為宙康部分電抗器的價格和體積,同等電壓等級下電抗器電感量越小,體積越大,成本就越高,綜合考慮選用電感量為0.47 mH的電抗器,而根據電壓占比法選取0.28 mH的電抗器。
4 仿真分析
本文對引入兩種不同方案得到的電抗器(AC=0.47 mH和'AC=0.28 mH)進行建模和仿真實驗,并對仿真結果進行對比分析。其中電源部分為380 V/50 Hz的三相交流電,負載為7.5 Ω的電阻,取濾波電容=3000 μF。
表3為三種方案仿真結果,其中輸入功率因數在引入0.47 mH的電抗器后有明顯提升,整流輸出電壓紋波系數也顯著降低,但電感電壓占比會相對較大。圖(2a)和(2b)分別為基于兩種方案引入電抗器的電流傅立葉分析圖,在未引入電抗器時輸入電流諧波畸變率為94.60%,在引入0.28 mH的電抗器后諧波畸變率降為64.17%,而在引入0.47 mH的電抗器后諧波畸變率改善到了43.20%,這說明該電抗器較電壓占比法有較明顯的抑制效果。

圖2兩種情況下的傅立葉分析圖
圖3為兩種方案的輸出電壓電流仿真比較圖,其中引入0.28 mH的電抗器浪涌電流在850 A左右,而引入0.47 mH電抗器后浪涌電流縮小到接近660 A,這表明多目標優化算法在抑制浪涌電流方面效果較電壓占比法更加明顯。圖中引入0.28 mH的電抗器整流輸出電壓有效值為506.9 V,而在引入0.47 mH的電抗器的電路輸出電壓為502.2 V,多目標優化算法所得的電抗器較常規方案電抗器電感量大,電抗器電壓占比也就大,所以前者的整流輸出電壓高。

圖3 三種狀況輸出電壓電流波形圖

5 結論
高頻開關電源的整流電路造成的諧波是不可避免的,后級的濾波電容器也會在電源開通時產生較高的浪涌電流和過電壓,引入輸入電抗器非常必要。本文以電抗器的壓降問題、線路中的諧波種類、輸入功率因數、輸入電壓諧波畸變率、輸出電壓紋波、體積成本等作為研究對象,并運用多目標優化的方法對多個子目標進行優化處理,得到了最合適的電抗器電感量。并通過仿真分析表明該方法得到的電抗器在抑制輸入電壓諧波、降低輸出沖擊電流、減小輸出電壓紋波等方面較電壓占比法效果更好,系統性能得到改善。
[1] Umihani? M. Analyze of higher harmonic six pulse rectifier transformer connection [J]. Technical Journal. 2015, 9(1).
[2] 孫媛媛, 王小宇,尹志明. 三相整流裝置諧波產生機理分析及簡化模型[J]. 電力系統自動化, 2012, (07): 51-56.
[3] 馬慧霞. 變頻器諧波干擾的形成及抑制措施[J]. 自動化與儀器儀表, 2015, (06): 173-174.
[4] 馬超, 趙彥珍, 馬西奎. 基于等電流相位法的單相干式空心電抗器設計[J]. 電工技術學報, 2017, 32(10): 190-195.
[5] 孫錦,方超,曹亮. 變頻器輸入電抗器及直流濾波電容器的設計[J]. 應用科技, 2014, (02): 16-20.
[6] 黎冰. 變頻器實用手冊[M]. 化學工業出版社, 2011.
[7] Talbi E, Mostaghim S, Okabe T, et al. Multiobjective optimization[M]. Springer Berlin Heidelberg.
[8] Zitzler E, Thiele L. An Evolutionary algorithm for multiobjective optimization: The Strength Pareto Approach[J]. 1998.
[9] 王晗丁. 復雜問題的多目標進化優化算法研究[D]. 西安電子科技大學, 2015.
[10] 馬小姝,李宇龍, 嚴浪. 傳統多目標優化方法和多目標遺傳算法的比較綜述[J]. 電氣傳動自動化, 2010, (03): 48-50.
[11] 李光, 吳祈宗. 基于結論一致的綜合評價數據標準化研究[J]. 數學的實踐與認識, 2011, (03): 72-77.
Parameter Design of AC Reactor Based on Multi-objective Optimization Algorithm
Zhang Huajun, Huang Peng, Su Yixin
(School of Automation, Wuhan University of Technology, Wuhan 430070, China)
TM47
A
1003-4862(2018)01-0001-04
2017-10-15
湖北省自然科學基金資助項目(2016CFB502,2015CFB586)
張華軍(1980-),男,副教授。專業方向:電力電子與電氣傳動。

