定子繞組等效模型對電機熱計算結果影響研究
萬 里,熊 用,祝后權
?
定子繞組等效模型對電機熱計算結果影響研究
萬 里,熊 用,祝后權
(武漢船用電力推進裝置研究所,武漢 430064)
在電機熱計算中,由于定子繞組結構比較復雜,一般對其進行相應的等效簡化處理,但對相關處理方法的理論支撐及對溫升計算結果的影響很少進行深入研究。本文主要針對定子繞組常用的兩種等效形式進行相關研究,首先對不同模型進行理論分析,再通過三維仿真計算,對不同形式的溫升結果進行評估和對比,得到相關的結論,可用于指導提高電機熱計算的準確度。根據仿真結果可知,絕緣材料對定子繞組的散熱影響較大,將全部繞組等效為一個整體分布在槽中間,絕緣均勻分布在其周圍的假設所得結果最接近實際情況。
定子繞組 等效 網格劃分 仿真模型
0 引言
電機的熱設計是電機設計的重要部分,它關乎著電機的使用壽命和穩定性等各方面的性能。電機定子繞組結構較為復雜,對它進行實體建模計算會花費大量的時間和精力,一般會根據其結構特點進行等效假設。現在常見的處理方法有兩種,一種是將全部的繞組等效為一個整體分布在槽中間,絕緣部分均勻的分布在其周圍;另一種等效則是直接將繞組和絕緣等效在一起成為一個整體。不同的簡化模型將會導致計算結果的差異,需要對等效模型的準確性和適用條件進行研究,從而評估這些差異帶來的影響。本文將針對定子繞組的等效形式進行相關研究,旨在找出相關結論,為后續電機熱計算提供參考。
1 國內外研究現狀
目前國內外針對電機熱設計的研究很多,但很少針對繞組等效假設進行專門研究,大多數文章中都是直接將槽內繞組等效為一個整體分布在槽中心,將絕緣部分簡化為均勻分布。
胡萌對船用高功率密度永磁發電機的溫度場的分析,直接構造了定轉子的整體溫度場模型,將雙層繞組等效為單層繞組,繞組端部等效為直線形式[1];史忠震等對電機定子繞組熱模型等效方法進行分析研究,根據槽滿率將繞組等效為一個整體,外層由絕緣材料包裹[2];張炳義等對永磁電機熱負荷分析,電機是雙層繞組,根據假設將上下兩層繞組分別等效為兩個個整體;胡淑環對永磁電機熱計算研究,也是將雙層繞組分別等效為兩個整體,而且還把槽簡化為規則的形狀[3];汪文博研究永磁同步電機的熱路模型,將繞組等效為銅導熱體,集中分布在槽的中心,槽內的其他材料等效為同質的絕緣到熱體[4];舒圣浪永對高速磁電機溫度場與流體場進行了計算研究,把槽內導體等效為均勻銅條,將定子槽內各絕緣以及空氣等效為絕緣實體,端部繞組以平均半匝長做平直化處理[5]。
國外A.G.Sarigiannidis等人對牽引用永磁電機的熱分析和性能評估中,將電機的繞組等效為一個整體均勻分布在槽中心[6];B.Funieru對一款牽引用永磁電機進行熱設計,對雙層繞組分別等效為兩個整體均勻分布[7];AlirezaSiadatan對一型開關磁阻電機的熱穩定性進行有限元分析,其中電機繞組直接等效為一個均勻的整體[8]。
由此可見,國內外對電機進行熱設計和熱分析時,繞組一般都是作整體等效處理,但不足之處是很多文章都沒有給出相應的理論證明、適用條件和不同模型對結果偏差。為了進一步研究繞組等效形式的使用范圍和有效性,現作相關的研究和討論。
2 理論推導
2.1 基本模型
根據國內外文中提到的簡化假設模型,具體將其歸納為以下兩種情況。第一是將所有繞組等效為一個整體,絕緣均勻分布在其四周,稱為假設一模型;第二種是將繞組和絕緣等效為一個整體,稱為假設二模型。它們的示意圖見圖1。


2.2 理論推導
根據電機定子的傳熱路徑,現研究其一維導熱情況。在X軸方向上,最大溫差在模型中間,假設一與原模型由于導熱熱阻相同,得到的最大溫升相同;在Y軸方向上可以分為兩種情況,根據導熱計算公式,對三種模型的溫升理論結果推導如下:
當下端絕熱,熱量全部沿Y軸正方向傳導,此時模型最下端具有最大溫差。
原模型的溫差為

假設一模型的溫差為
假設二模型可以看作是具有內均勻熱源Ф的導熱問題。
當在Y軸方向上正負同時導熱,且上下兩端導熱條件完全相同時,中間溫差最大。
原模型的溫差為

假設一的溫差為
假設二的溫差為

外熱源的情況,最大溫差可以表示為
2.3 理論結果比較
各假設等效模型的導熱最大溫差如下表1所示。根據表1可知:當熱量在x軸方向上單獨傳導時,假設一與原模型的最大溫差相同,在后面的計算討論中不再考慮x軸方向上的情況;在y軸方向上單邊傳熱時,假設一與原模型情況一致,雙邊傳熱時假設一的最大溫差會大于原模型;假設二也要考慮等效導熱系數,在與外熱源的模型對比時,假設二的最大溫差較小。

3 三維仿真計算
3.1模型建立及網格劃分
本文的研究對象是一型永磁電機,雙層繞組結構。根據上文中的等效方法,建立如下三種仿真模型。

如圖2所示為原模型和三種假設等效形式。A表示原模型;B表示假設一,將繞組等效為上下兩部分,分別由絕緣包裹;C表示假設二,將上、下層繞組和絕緣分別等效為兩個整體;C表示假設三,把所有繞組和絕緣全部等效為一個整體。
利用ICEM-CFD軟件對上述四種模型進行結構化網格劃分,得到如圖3結果。
3.2邊界條件設置
在第二和第三種等效模型中,由于將繞組和絕緣都等效為一個整體,所以要計算出它的等效導熱系數,具體公式如下。


在進行模型進行仿真時,只考慮鐵心上端散熱,將其設為散熱面,其他壁面設為絕熱。繞組導線的生熱量給定,具體數據如下表4。
3.3 網格無關性分析
為了驗證網格的無關性,現對等效模型三進行不同網格數的仿真,分別將其劃分為十萬數級網格和五十萬數級網格,得到的仿真結果如下圖。

由圖4可以看出,當等效模型一致,外部傳熱條件等都相同時,網格數量對最終的傳熱結果影響甚微。在后面的仿真中,所有模型都采用十萬級網格進行計算。
圖4 網格數比較
3.4各模型結果對比
根據前文中所得到的各材料的導熱系數,取絕緣導熱系數,槽楔導熱系數和墊塊導熱系數都取0.2W/(m·K),網格數取十萬級,得到的仿真結果如圖5。

圖5 各模型仿真結果
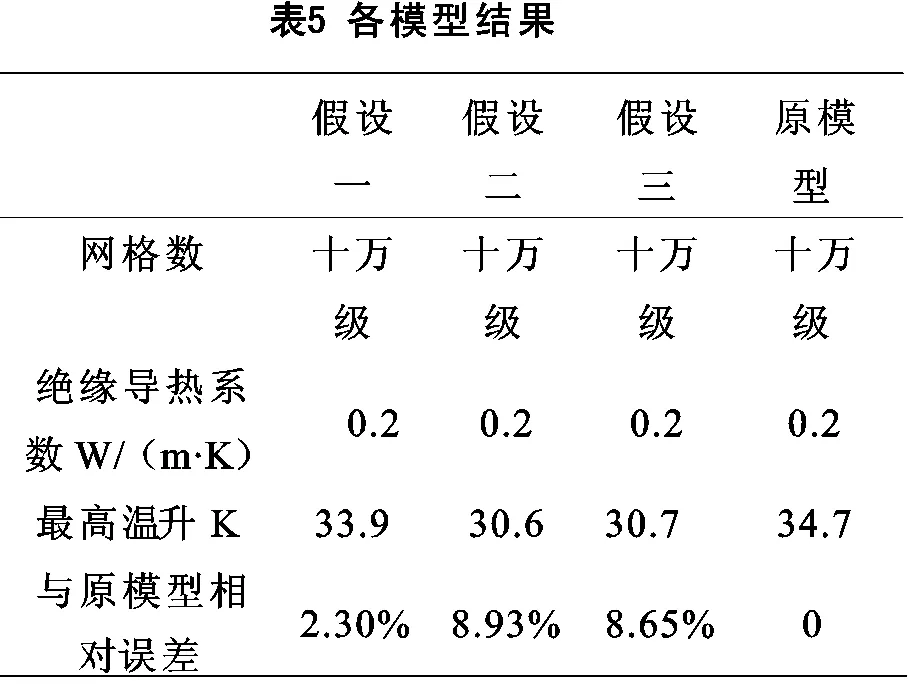
各種模型所得的結果如表5。
4結束語
1)本文對定子繞組熱計算時常用的幾種假設進行理論推導和仿真計算,驗證了假設的合理性和準確性。2)根據仿真結果可知,假設一所得到的結果最接近原模型,假設二與假設三的結果稍小于原模型。3)各模型的優缺點和適用條件見下表。

[1] 胡萌. 船用高功率密度永磁發電機的溫度場研究.[碩士學位論文]. 上海:上海交通大學,2014.
[2] 史忠震. 電機定子繞組熱模型等效方法的研究[J]. 制造技術與機床, 2015, 12:103-106.
[3] 張炳義. 潛油泵直驅單元組合式永磁電機熱負荷分析[J]. 微電機, 2014, 47(7):1-4.
[4] 汪文博. 永磁同步電機的熱路模型研究[碩士學位論文]. 浙江:浙江大學, 2014.
[5] 佟文明, 程血雪斌, 舒圣浪. 高速磁電機流體場與溫度場的計算分析[J]. 電工電能新技術, 2016, 35(5):23-28.
[6] A.G.Sarigiannidis,M.E. Performance evaluation and thermal analysis of interior permanent magnet traction motor over a wide load range.IEEE Electrical Machines,doi:10.1109/ICELMACH, 2016. 7732897, 2016.
[7] B. Funieru, A. Binder Thermal. Design of a permanent magnet motor usedfor gearless railway traction. IEEE Industrial Electronics, 2008: 2061-2066.
[8] AlirezaSiadatan,S.H.Mirimani,MahshidShamei,TohidKhalili.Thermal stability Analysis of 6/4 switchreluctance motor using finite element method.International SymposiumonPowerElectronics , 2016 :382-387.
Influence of Stator Winding Equivalent Form on Thermal Calculation of Motor
Wan Li, Xiong Yong, Zhu Houquan
(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)
TM34
A
1003-4862(2018)01-0061-04
2017-11-15
萬里(1991-),男,碩士研究生。研究方向:電機與電器。

