具有次近鄰相互作用的五量子比特XXZ海森伯自旋鏈的熱糾纏?

劉貴艷 毛竹 周斌

(湖北大學物理與電子科學學院，武漢 430062)

1 引 言

量子糾纏作為量子系統中的最基本特征之一,因其所特有的物理性質,在量子計算與量子信息領域中得到了廣泛的應用,例如量子隱形傳態[1]、量子超密編碼[2]以及量子秘鑰分發[3]等.在固態系統中實現與調控量子糾纏是人們關注的研究熱點.海森伯自旋鏈作為一種簡單的固態量子體系已成為人們研究量子糾纏的理想模型之一.眾所周知,體系的量子效應會受到環境溫度的重要影響,熱漲落將抑制量子效應的產生.在量子糾纏態的制備中溫度被看成是一個非常重要的調控參數,人們由此提出熱糾纏的概念.Arnesen等[4]首次在海森伯模型中研究了熱糾纏的性質,隨后人們對各種兩量子比特海森伯模型和多量子比特海森伯模型的熱糾纏和配對糾纏特性開展了廣泛的理論研究[5?14].研究表明,溫度、磁場、自旋相互作用的各向異性和Dzyaloshinkii-Moriya(DM)相互作用等各種參數的變化都對體系熱糾纏性質起到重要的調控作用.

在海森伯自旋鏈模型熱糾纏的研究中,人們較多考慮的是最近鄰量子比特自旋相互作用.實際上,一種J1-J2海森伯模型也引起了人們的研究興趣,該模型中同時考慮了最近鄰自旋相互作用和次近鄰自旋相互作用[15,16].在J1-J2海森伯模型中,由于次近鄰相互作用的引入導致阻挫效應,對體系的磁性有著重要的影響.研究發現,在一些準一維化合物中,如CuGeO3[17]和NaV2O5[18]等存在次近鄰自旋相互作用.最近,有一些理論工作研究了具有次近鄰相互作用的多量子比特海森伯模型中的糾纏性質[19?26].如Gu等[19]研究了溫度和次近鄰相互作用參數的變化對具有次近鄰相互作用的一維海森伯自旋鏈中最近鄰量子比特及次近鄰量子比特配對糾纏的影響.他們數值計算了該自旋的體系中糾纏消失所對應的臨界溫度.Liu等[23]研究了具有次近鄰相互作用的三量子比特XXX海森伯模型在非均勻磁場作用下的配對熱糾纏性質. ?ahinta?和Akyüz[26]研究了具有次近鄰相互作用的四量子比特XXZ海森伯模型中的糾纏性質.他們重點討論了DM相互作用和阻挫參數對最近鄰量子比特及次近鄰量子比特配對糾纏的影響.

本文研究具有次近鄰相互作用的五量子比特XXZ海森伯模型中的熱糾纏性質;利用數值計算方法分別計算最近鄰量子比特和次近鄰量子比特共生糾纏度;研究上述兩種共生糾纏對隨溫度、磁場強度、DM相互作用、自旋相互作用及阻挫參數的變化關系;給出理論模型和糾纏度的計算方法,以及糾纏度的數值計算結果,并討論各參數對糾纏度的影響.

2 理論模型和糾纏度

2.1 理論模型

研究的具有次近鄰相互作用五量子比特XXZ海森伯自旋鏈模型如圖1所示,系統哈密頓量H由下式給出:

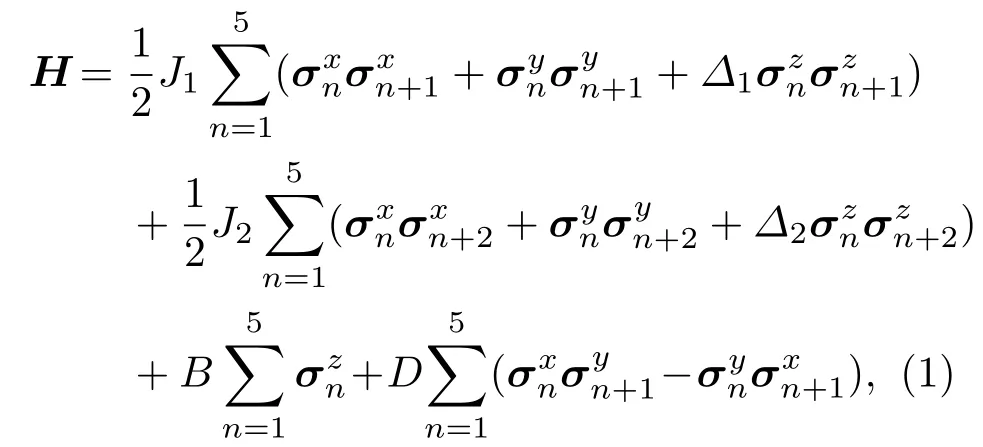
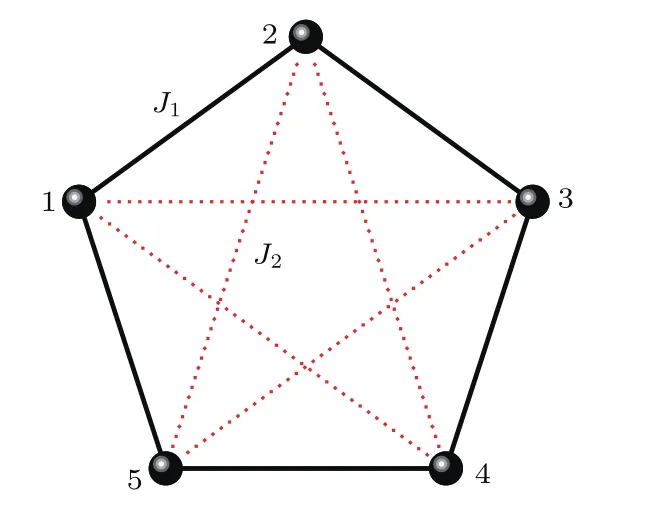
圖1 五量子比特海森伯自旋鏈示意圖 黑色點代表自旋1/2的量子比特,黑色實線代表最近鄰相互作用記為J1,紅色虛線代表次近鄰相互作用記為J2Fig.1.Five-qubit Heisenberg spin chain.The black dot represents a qubit with spin 1/2,the black lines represent the interaction between the nearest neighboring qubits named as J1,and the red dashed lines represent the interaction between the next nearest neighboring qubits named as J2.

2.2 糾纏度

哈密頓量(1)式的本征值和對應的本征矢分別為En和|ψn〉(n=1,2,···,32),在溫度為T時,系統的密度矩陣為

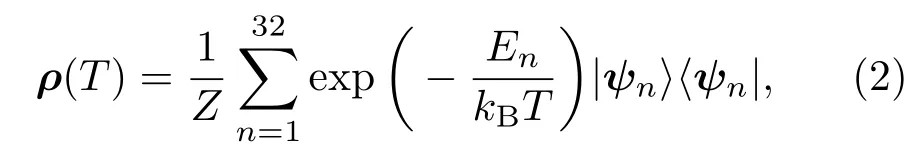
其中Z為系統的配分函數

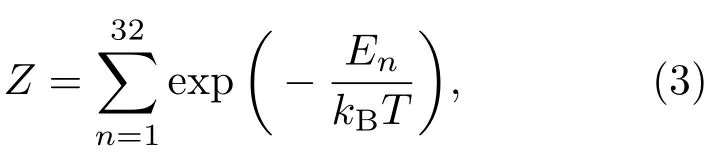
計算中取玻爾茲曼常數kB=1.

為了研究上述五量子比特海森伯自旋鏈的糾纏性質,計算第i個量子比特和第j個量子比特之間的共生糾纏度Cij,共生糾纏度的定義為[27?29]

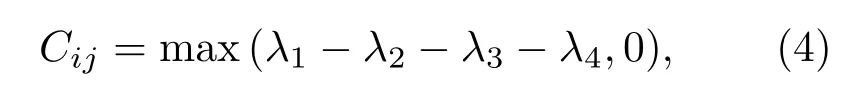
其中λn是算子Rij的本征值的平方根,Rij定義為

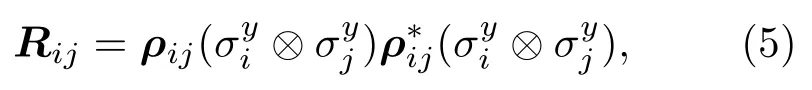
λn按降序排列,即λ1≥λ2≥λ3≥λ4;ρij是約化密度矩陣,是ρij的復共軛矩陣;糾纏度Cij的取值由0到1,Cij=0表示無糾纏,Cij=1表示系統處于最大糾纏態,0＜Cij＜1表示部分糾纏.根據圖1中自旋鏈結構的對稱性,下面分別討論最近鄰兩量子比特的共生糾纏度C12與次近鄰兩量子比特共生糾纏度C13隨參數的變化關系.

3 結果與討論

基于共生糾纏度的定義,用數值計算方法研究具有次近鄰相互作用五量子比特XXZ海森伯自旋鏈模型熱糾纏性質,分別求解最近鄰兩量子比特共生糾纏度C12和次近鄰兩量子比特共生糾纏度C13在不同的溫度、磁場強度、DM相互作用參數及各向異性參數下隨阻挫參數的變化關系.

3.1 磁場與溫度對C12和C13的影響

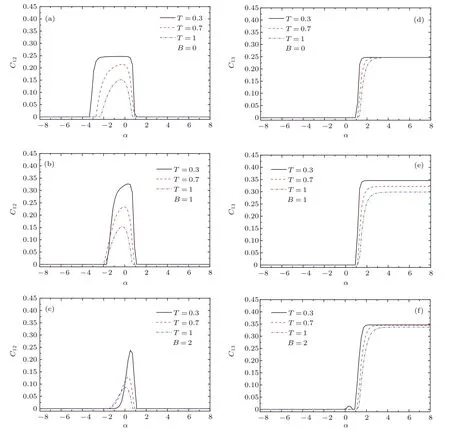
圖2 在不同溫度和磁場強度下,C12和C13隨阻挫參數α變化情況 (a),(d)B=0;(b),(e)B=1;(c),(f)B=2;這里取D=0,Δ1=Δ2=1和J1=1Fig.2.C12and C13versus frustration parameter α for different temperature and magnetic fi eld:(a)and(d)B=0;(b)and(e)B=1;(c)and(f)B=2.Here,D=0,Δ1=Δ2=1 and J1=1.

首先考慮DM相互作用為零(D=0)的情形.當各向異性參數Δ1=Δ2=1時,即系統由各向異性的XXZ自旋模型轉變為各向同性的XXX自旋模型,在不同磁場和溫度下,C12和C13隨阻挫參數的變化關系由圖2給出.從圖2(a)中可以發現,在沒有磁場作用下(B=0),溫度較低時(如T=0.3)C12在阻挫參數?3.3＜α＜1.0區間出現一個非零的平臺(C12=0.25).這表明,阻挫參數絕對值的增大將壓制最近鄰兩量子比特糾纏的產生.隨著溫度的升高,出現糾纏(C12不為零)的阻挫參數區間逐漸縮小,而且伴隨著C12最大值的減小.如當溫度分別為T=0.7和T=1時,出現糾纏的阻挫參數區間分別為(?2.7,0.9)和(?2.3,0.7),相應的C12最大值為0.21和0.15.圖2(b)和圖2(c)顯示,在同樣的溫度下,出現糾纏的阻挫參數區間隨著磁場強度的增加而縮小.以溫度T=0.7為例,磁場強度分別為B=1和B=2時,出現糾纏的阻挫參數區間分別為(?2.0,0.9)和(?1.4,0.9).圖2(d)—(f)給出了次近鄰兩量子比特共生糾纏度C13隨阻挫參數的變化關系.顯然,C13表現出與C12完全不同的變化關系.次近鄰兩量子比特共生糾纏度C13不為零出現在阻挫參數α＞1,而α＜1時次近鄰兩量子比特配對糾纏消失.以T=0.3為例,當磁場為零時(如圖2(d)所示),當α＞1,隨α的增加,C13迅速達到最大值0.25并保持不變.當磁場強度增加時,如B=2,C13的最大值提高到0.35,同樣對于α＞1,C13隨α的增加迅速飽和并保持不變.這表明,對于反鐵磁情形(J1,J2＞0)而言,當次近鄰相互作用參數大于最近鄰相互作用參數時,有利于次近鄰兩量子比特配對糾纏的產生,而最近鄰兩量子比特糾纏消失.

為了更進一步討論磁場對C12和C13的影響,取溫度T=0.3為例,計算了隨磁場和阻挫參數變化的共生糾纏度,結果由圖3給出(圖3中藍色區域代表糾纏度為零,紅色最深的區域對應糾纏度為0.35).從圖3(a)中可以看出,隨著磁場增大,一方面出現最近鄰量子比特糾纏的區域逐漸縮小,另一方面共生糾纏度C12先增大后逐漸減小直至消失.同時發現,當磁場超過一定強度（B＞2.5）時,出現糾纏的區域被限制在一個很窄的參數空間內(見圖3(a)中淺藍色區域),而且共生糾纏度C12也被壓制在0.1以內.圖3(b)對應共生糾纏度C13的變化情況.在磁場小于3時,出現次近鄰量子比特糾纏的區域大致保持不變,而磁場超過3時,產生糾纏的臨界阻挫參數隨磁場增大逐漸增大.在圖3(b)中,隨著磁場和阻挫參數的變化,存在使得共生糾纏度達到飽和值C13=0.35的一個較大參數區域.

當考慮自旋相互作用各向異性時(取Δ1=Δ2=0.5),C12和C13隨阻挫參數變化關系由圖4給出.比較圖2和圖4發現,自旋相互作用各向異性對上述兩種共生糾纏度都有顯著的影響.以T=0.3為例,當磁場為零時,C12不為零的阻挫參數區有兩個(見圖4(a)),即分別是?2.5＜α＜0.9和α＜?3.6,第一個參數區的范圍相對于各向同性時(Δ1=Δ2=1,見圖2(a))略有縮小;而第二個參數區是各向同性時所沒有的.隨著磁場的增加,存在糾纏的第一個阻挫參數區相應的C12的值減小,即最近鄰兩量子比特糾纏受到磁場的抑制;對于第二個參數區而言,磁場反而有利于最近鄰兩量子比特糾纏的產生(見圖4(b)和(c)).同樣,隨著阻挫參數的變化,次近鄰兩量子比特糾纏不為零的參數區也有兩個,分別是1＜α和α＜?2.7(當T=0.3和B=0時,見圖4(d)),其中第一個參數區類似于各向同性的情形(見圖2(d)),而在第二參數區則是由自旋相互作用各向異性誘導出次近鄰兩量子比特間的配對糾纏.對于其他一定的溫度和磁場強度,也存在著對應C13不為零的與上述情形相似的阻挫參數區(見圖4(e)和(f)).如,當T=1和B=1時,對應于1.2＜α和α＜?3.3,存在次近鄰兩量子比特配對糾纏(即C13/=0).

在自旋相互作用各向異性的情形下,同樣取溫度T=0.3為例,圖5給出了共生糾纏度C12和C13隨磁場和阻挫參數變化的等高圖.與圖3(a)比較,不難發現,在自旋相互作用各向異性的情形下,圖5(a)顯示共生糾纏度C12在阻挫參數較大的負值區間出現新的糾纏區.在這個新的糾纏區,隨磁場增大,C12先逐漸增大至最大值,后被抑制直至消失.同樣,對于C13而言(如圖5(b)所示),與圖3(b)比較,考慮到自旋相互作用各向異性,在阻挫參數較大的負值區間也出現了新的糾纏區.特別是當阻挫參數取較大的負值時,如α=?8,C13隨磁場增大出現了兩個極大值.

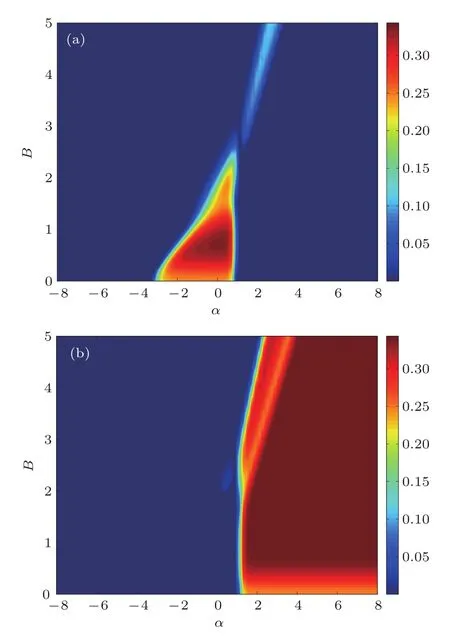
圖3 共生糾纏度隨阻挫參數α及磁場強度變化情況 (a)C12;(b)C13;這里取T=0.3,D=0,Δ1=Δ2=1和J1=1Fig.3. Concurrence versus frustration parameter α and magnetic fi eld:(a)C12;(b)C13.Here,T=0.3,D=0,Δ1=Δ2=1 and J1=1.

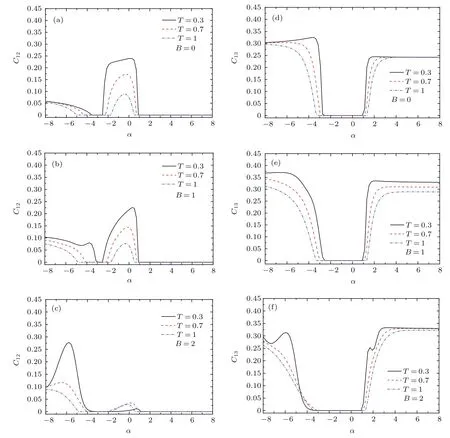
圖4 在不同溫度和磁場強度下,C12和C13隨阻挫參數α變化情況 (a),(d)B=0;(b),(e)B=1;(c),(f)B=2;這里取D=0,Δ1=Δ2=0.5和J1=1Fig.4.C12and C13versus frustration parameter α for different temperature and magnetic fi eld:(a)and(d)B=0;(b)and(e)B=1;(c)and(f)B=2.Here,D=0,Δ1=Δ2=0.5 and J1=1.

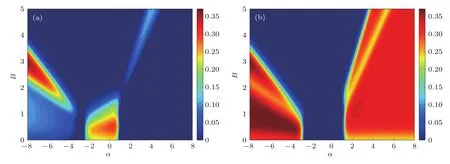
圖5 共生糾纏度隨阻挫參數α及磁場強度變化情況 (a)C12;(b)C13;這里取T=0.3,D=0,Δ1=Δ2=0.5和J1=1Fig.5.Concurrence versus frustration parameter α and magnetic fi eld:(a)C12;(b)C13.Here,T=0.3,D=0,Δ1=Δ2=0.5 and J1=1.

3.2 DM相互作用對C12和C13的影響

下面研究DM相互作用對共生糾纏度的影響.在各向異性參數Δ1=Δ2=0.5的情形下,圖6和圖7給出了對應于不同溫度、磁場強度及DM相互作用參數,最近鄰兩量子比特共生糾纏度C12和次近鄰兩量子比特共生糾纏度C13隨阻挫參數的變化情況.

圖6(a)—(c)給出了沒有外加磁場(B=0)時C12隨阻挫參數變化情況.顯然,在一定的阻挫參數區域，DM相互作用有利于最近鄰兩量子比特配對糾纏的產生.以T=0.7為例,當不考慮DM相互作用時(D=0,見圖4(a)),最近鄰兩量子比特共生糾纏度C12不為零的阻挫參數區有兩個,即分別是?2.2＜α＜0.8和α＜?4.2;當考慮DM相互作用時(見圖6(a)—(c)),隨DM 相互作用參數的增大,C12最大值增大,如D=0.5,1,2相對應的C12最大值分別是0.28,0.32,0.33.而且,C12不為零的第一個阻挫參數區的范圍變大,如D=0.5,1,2相對應的C12不為零的第一個阻挫參數區的范圍分別是?2.6＜α＜1,?3.3＜α＜2.9和?4.1＜α＜6.1;同時也注意到隨DM相互作用參數的增大,C12不為零的第二個阻挫參數區向左偏移.圖6(d)—(i)給出了有外加磁場時C12隨阻挫參數變化情況.顯然,在有外加磁場時,DM相互作用對最近鄰兩量子比特配對糾纏的影響與無磁場時定性一致.

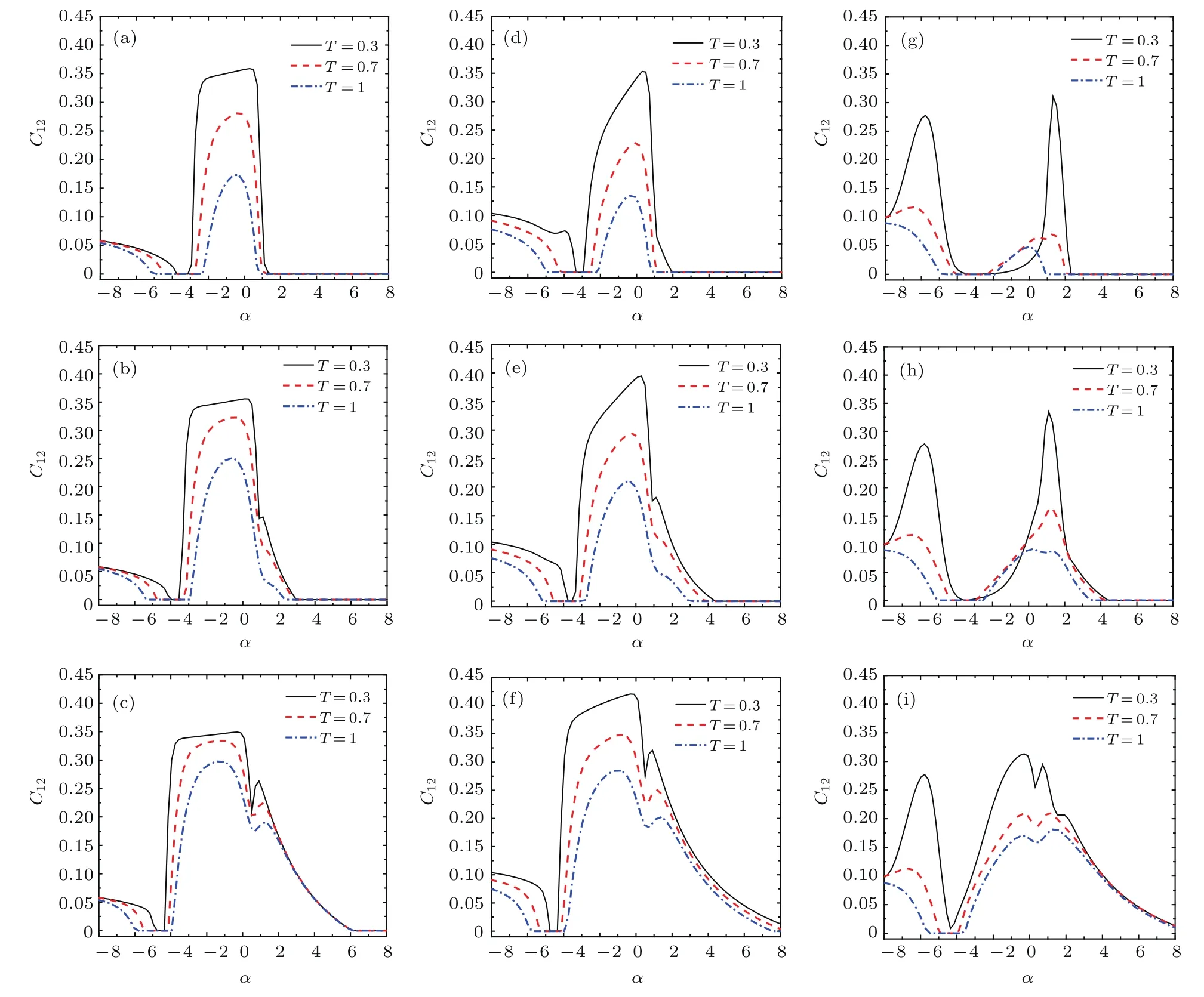
圖6 在不同溫度、磁場強度和DM相互作用參數下,C12隨阻挫參數α變化情況,Δ1=Δ2=0.5和J1=1 (a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2Fig.6.C12versus frustration parameter α for different temperature,magnetic fi eld and DM interaction parameter,Δ1= Δ2=0.5 and J1=1:(a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2.

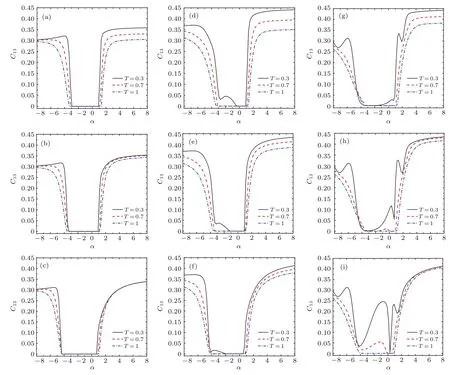
圖7 在不同溫度、磁場強度和DM相互作用參數下,C13隨阻挫參數α變化情況,Δ1=Δ2=0.5和J1=1 (a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2Fig.7.C13versus frustration parameter α for different temperature,magnetic fi eld and DM interaction parameter, Δ1=Δ2=0.5 and J1=1:(a)B=0,D=0.5;(b)B=0,D=1;(c)B=0,D=2;(d)B=1,D=0.5;(e)B=1,D=1;(f)B=1,D=2;(g)B=2,D=0.5;(h)B=2,D=1;(i)B=2,D=2.

圖7(a)—(c)給出了沒有外加磁場(B=0)時C13隨阻挫參數的變化情況.不難發現,隨著DM相互作用的增強,相應次近鄰兩量子比特共生糾纏度C13為零的阻挫參數區域增大.以T=0.7為例,對應于D=0.5,1和2時,C13為零的阻挫參數區域分別是(?3.1,1.1),(?3.4,1.1)和(?4.2,1.0). 而且在α＞1區域,隨著DM相互作用的增強,溫度對C13的影響受到抑制.當考慮磁場的作用時,在一定的磁場范圍內,如B=1時(見圖7(d)—(f)),DM相互作用對次近鄰兩量子比特配對糾纏的影響與無磁場時也是定性一致的.當磁場適當增加時,如B=2時(見圖7(g)—(i)),DM相互作用的增強使得原先C13為零的阻挫參數區在溫度較低時(如T=0.3)也產生了次近鄰兩量子比特配對糾纏.

4 結 論

基于數值計算方法求解共生糾纏度,研究了具有次近鄰相互作用的五量子比特XXZ海森伯自旋模型熱糾纏性質.分別討論了最近鄰兩量子比特和次近鄰兩量子比特共生糾纏度隨系統各種調控參數的變化規律.研究結果表明,阻挫參數的變化對上述兩種共生糾纏度的影響表現出不同的性質.例如,對于反鐵磁情形而言,當次近鄰相互作用參數大于最近鄰相互作用參數時,有利于次近鄰兩量子比特配對糾纏的產生,而最近鄰兩量子比特的糾纏消失.同時發現,溫度、磁場、DM 相互作用以及各向異性參數對配對糾纏有著不同程度的影響.因此,通過選擇適當的模型參數,可以有效地調節和提高五量子比特XXZ海森伯自旋鏈的共生糾纏度.

[1]Bennett C H,Brassard C,Crépeau C,Jozsa R,Peres A,Wootters W K 1993Phys.Rev.Lett.70 1895

[2]Bennett C H,Wiesner S J 1992Phys.Rev.Lett.69 2881

[3]Ekert A K 1991Phys.Rev.Lett.67 661

[4]Arnesen M C,Bose S,Vedral V 2001Phys.Rev.Lett.87 017901

[5]Wang X G 2001Phys.Rev.A64 012313

[6]Wang X G 2001Phys.Lett.A281 101

[7]Zhang Y L,Zhou B 2011Acta Phys.Sin.60 120301(in Chinese)[張英麗,周斌 2011物理學報60 120301]

[8]Cao M,Zhu S Q 2005Phys.Rev.A71 034311

[9]Wang X G,Fu H C,Solomon A I 2001J.Phys.A34 11307

[10]Hou J M,Du L,Ding J Y,Zhang W X 2010Chin.Phys.B19 110313

[11]Wang Y H,Xia Y J 2009Acta Phys.Sin.58 7479(in Chinese)[王彥輝,夏云杰 2009物理學報 58 7479]

[12]Hu Z N,Yi K S,Park K S 2007J.Phys.A:Math.Theor.40 7283

[13] ?uczak J,Bu?ka B R 2012J.Phys.:Condens.Matter24 375303

[14]Zhou B 2011Int.J.Mod.Phys.B25 2135

[15]Majumdar C K,Ghosh D K 1969J.Math.Phys.10 1388

[16]Majumdar C K,Ghosh D K 1969J.Math.Phys.10 1399

[17]Hase M,Terasaki I,Uchinokura K 1993Phys.Rev.Lett.70 3651

[18]Bray J W,Interrante L V,Jacobs L S,Bonner J C 1983Extended Linear Chain Compounds(Volume 3)(New York:Plenum Press)pp353–415

[19]Gu S J,Li H,Li Y Q,Lin H Q 2004Phys.Rev.A70 052302

[20]Eryi?it R,Gündü? Y,Eryi?it R 2006Phys.Lett.A358 363

[21]Eryi?it R,Gündü? Y,Eryi?it R 2006Phys.Lett.A349 37

[22]Chhajlany R W,Tomczak P,Wójcik A,Richter J 2007Phys.Rev.A75 032340

[23]Liu R,Liang M L,Yuan B 2007Eur.Phys.J.D41 571

[24]Eryi?it R 2009Int.J.Theor.Phys.48 885

[25]Kwek L C,Takahashi Y,Choo K W 2009J.Phys.:Conf.Ser.143 012014

[26] ?ahinta? A,Akyüz C 2016Physica A448 10

[27]Hill S,Wootters W K 1997Phys.Rev.Lett.78 5022

[28]Wootters W K 1998Phys.Rev.Lett.80 2245

[29]Coffman V,Kundu J,Wootters W K 2000Phys.Rev.A61 052306