外場對分子納米結電流-電壓特性的影響?

牛璐 王鹿霞

(北京科技大學數理學院,北京 100083)

1 引 言

隨著高性能計算的市場需求和納米光刻技術的發展,半導體硅晶材料組成的集成電路已遠不能滿足市場的要求,分子電子學器件由于具有高靈敏度、高穩定性和低功耗等特征而受到廣泛關注,同時掃描隧道顯微鏡和原子力顯微鏡的發展為相應的實驗研究開創了條件,電極-電解質體系中的非絕熱電子輸運問題[1,2]的研究也促進了分子電子學理論的開展.

由金屬電極/分子/金屬電極組成的分子納米結(如圖1所示)作為分子電子器件的基本單元,深入理解其光電特性至關重要.由于分子具有多樣化的結構特點,不同的分子納米結可以具有開關效應、整流效應、負微分電阻效應、場效應管效應、量子干擾效應等一系列重要特征[3?11].最近的研究還發現分子和電極之間的熱電相互作用[8]、電極的位形[5,9]以及分子的對稱性[11]的變化等都是影響器件電子輸運性質的重要因素,這些研究成果對發展小尺度、高速度、低功耗和高集成的分子器件提供科學支持.關于分子納米結的研究理論方法主要有密度矩陣動力學方程[12]、非平衡態格林函數法[4?11,13,14]、擴展主方程[15?17]、密度泛函理論[18]、散射理論[19]等.非平衡格林函數方法的優點是能夠將分子的電子結構計算與分子納米結的I-V特征計算有效結合,并可通過第一性原理計算方法和非平衡態格林函數理論研究分子的位置取向對分子納米結中電子輸運性質的影響[20].通過引入光子自能,非平衡態格林函數方法還可以考慮光場的作用[21?24],并對外場作用下的分子不同構型間的轉變導致的電流開關效應進行研究.擴展主方程作為密度矩陣描述的約化形式,可通過分子的勢能考慮電子與分子振動態的耦合和分子的電子激發態,實現對電子輸運過程中的光激發及其退激發過程的模擬,該方法對分子與電極弱耦合條件下的彈性電流具有獨到的優越性.文獻[25]使用了該方法研究了光激發作用下分子納米結上的電子輸運問題,并且在電子輸運過程中的電子轉移和能量轉移方面做出了很多深入的研究.在光激發作用下分子納米結的電子輸運問題,May課題組做了先驅性的工作,他們考慮分子中振動效應、弛豫效應、光激發效應等應用密度矩陣理論發展了研究分子納米結中非彈性電流的一般方法,并發現當分子納米結中受到一定強度的光激發時,新的電荷轉移通道打開,從而Franck-Condon阻滯現象消失[25,26].隨后May及其合作者研究了分子納米結的非平衡態振動效應、分子不同帶電態上的電荷輸運過程以及電極和分子受到光激發過程的熱效應等,但大部分理論研究只關注不同外界條件下分子達到穩定時的電流-電壓特性.然而分子在光激發過程中的瞬間行為是影響分子納米結以及分子電子器件穩定性的至關重要的因素,了解分子納米結電流達到穩定所需要的時間、瞬間電流在不同偏壓和不同脈沖作用下的響應時間等因素對深入理解分子納米結中的非彈性電流及其性質將有積極的意義.文獻[27]雖然研究了外場在開啟和關閉過程中的瞬間電流行為,但沒有針對不同偏壓下的瞬間行為做系統研究,對光激發過程中的自發輻射沒有深入探討.而通過掃描隧道顯微鏡實驗驗證分子納米結中分子振動頻率分布與光場的耦合可以引起分子內光子的自發輻射[28?32].在外場作用下,若激光場達到穩定值所用的時間小于或與電荷轉移過程中電荷在分子內駐留的時間相當的情況下,激光場強度隨時間變化的過程中通過分子納米結的電流必將變化,但由于電荷在分子內的非平衡態振動分布,電流不發生同步改變,研究瞬間電流是分子電子學中非常迫切的問題.

為了突出分子納米結的物理特性,本文不關注分子和電極的具體結構和位形特點,應用擴展主方程方法,通過分子納米結的非彈性電流、光激發特性、耗散特性等研究高斯型外場對分子納米結中瞬間電流的影響.

圖1 分子導電納米結示意圖,兩端為金屬電極,中間為分子Fig.1. Scheme of the molecular conducting nanojunction.Molecule is in the center of two metal leads.

2 物理模型及相關公式

為了描述分子內振動態的非平衡態分布,將分子態按照電子態和振動態展開,這種表象適合于分子與電極耦合的系統.當有電流通過分子納米結時,首先需要區分分子的帶電態.用N表示進入中性分子內電子的數目,相應的分子基態能表征為EN,由于分子在得到電子或失去電子過程中會伴隨著核的運動,因此EN可以理解為N帶電態時其勢能面的最小值,即在分子在帶電態N時分子平衡態的能量.

分子的帶電態是否穩定取決于不同帶電態間的能量差EN?EN?1與作用電極的化學勢μ0之間的關系,比如E1?E0＜μ0表明N=1單電子態穩定.引入關系式ΔE10=E1?E0?μ0,若ΔE10＞0表明中性態穩定.同時假設ΔE0?1＜0即中性態比單空穴態穩定.由于光激發作用在分子的基態和激發態之間,因此需要同時區分不同帶電態下的電子態.用ENa表示N=0,1和a=g,e時的能量(g表示電子基態,e表示電子激發態,本文中只考慮單電子輸運過程,其他輸運過程與單電子輸運過程類似,這里不考慮),振動量子數用μ表示,分子處于某個狀態時的能量用ENaμ≡?εα表示,α為復合量子數.這樣在絕熱近似下分子的波函數可以表示為ψα=χNaμφNa,其中φNa表示電子態,χNaμ表示相應的振動態.這里假設電子的輸運過程與某個簡正主坐標Q下的振動有關,分子的其他坐標與輸運過程不直接耦合,認為是次級坐標不出現在復合量子數α中,其對電子輸運的貢獻主要表現在能量耗散上,因此用分子內振動態的重新分布(IVR)過程來描述.

分子納米結的哈密頓量H分別由分子部分Hmol、電極部分Hlead、分子與電極的耦合部分Hmol-lead以及分子與外場的耦合Hmol-field(t)組成:

其中分子部分的哈密頓量為

其中α和β為復合量子數,包含了三個量子態信息,分別為電子態a=g,e、帶電態N=0,1和分子振動態v和μ.電極部分的哈密頓量寫成二次量子化形式,這里,左右電極分別表示為X=L和R,s為電子自旋,k為電極導帶電子的波矢,?ωXks是相對應于電子態|ks〉的本征能量.電極與分子之間相互作用的哈密頓量寫為

這個表達式中的電子湮滅和產生算符aXks和分別指左電極或右電極X=L,R,轉移積分用TX(N±1a,Nb,k)表示.電極可以看作是宏觀系統,由巨正則統計分布決定,具體參見文獻[26],這里不再贅述.

偶極近似下分子與外場與分子的相互作用項為

其中dαβ為α和β態間的分子偶極矩,E(t)為外場,具有如下形式:

E(t)為外場強度的包絡線,一般為高斯型脈沖;n為電場方向矢量,其頻率則為ω.高斯型脈沖的數學形式為:,其中τp為脈沖寬度,tp為脈沖最大值所對應的時間.當外場頻率與分子激發態能量共振時,分子被有效地激發.分子導電納米結兩端的電極存在偏壓時,電極的費米能級及與之耦合的中性分子態能級隨之改變,當|e|V/2＜ΔE10時,電子無法轉移至能量較高的帶電態上,出現所謂的Franck-Condon阻滯,當電壓繼續增加,分子納米結中有電流通過,描述電荷在兩個態間的傳輸率K滿足以下條件:

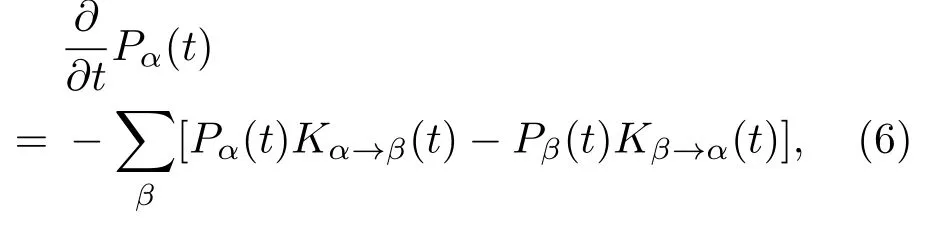
假設單電子輸運過程,則電極到分子的電荷傳輸率為

分子到電極的傳輸率為

其中NX為電極X上的電子態密度,U為電極和分子的耦合強度,這兩個物理量原則上都應與兩個態上的能量差ε1aμ,0bν有關.在本文的計算中將不區分分子的自旋,因此在此表達式中乘以2因子.

IVR引起的電荷轉移率在單振動反應坐標下的表示式為

其 中,n(ωvib)為 玻 色-愛 因 斯 坦 分 布 函 數,JMa(ωvib)為與次級振動坐標耦合的譜密度,由于反映主坐標內的勢能面為諧振子勢,譜密度只有在ωvib處有相應的值.

分子的光激發和光輻射率可以表示為

其中ω為外場頻率;為Rabi能,其表達式為,為外場包絡線與分子偶極矩的乘積.展寬系數γNaμ,Nbν表示在不同電子振動態間的轉移,由分子和電極間的耦合和IVR率共同決定.

由電極X到分子的電流為

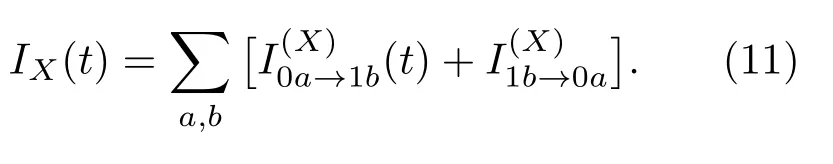
由于外場隨時間變化,電流隨時間t變化,表現瞬間特性.其兩部分電流的表達式分別為

分別表示分子得電子和失電子的過程,具體推導可參看文獻[25].需要注意的是這個電流成立的條件是外場的開關時間應該大于或可比于分子注入或流出電荷時間以及IVR的特征時間.

當電流達到穩定時,有IL=?IR,即從左電極流向分子的電流等于分子流向右電極的電流,在非穩定情況,有關系式

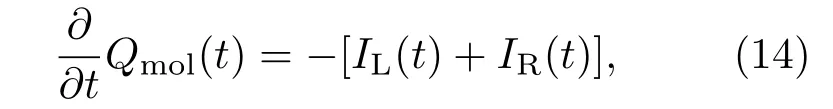
即從左電極到分子的電流和從右電極到分子的電流決定分子電荷的瞬間變化,其中分子電荷表示為

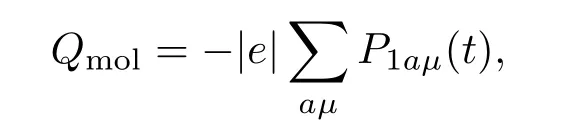
是帶電態上的電荷總和.

3 結果與討論

以下的計算將不關注某個特殊分子,而是采用分子和電極的一般參數給出通過子分子納米結中的穩定和瞬間電流.為了突出物理性質并簡化計算,我們采用了一些近似,如認為電極與分子直接耦合作用與其能量差無關,用常數表示,電極中的態密度也認為是常數,電極與分子間的電荷輸運與這兩個量均有關,用組合參數

表1 參數列表(具體說明見正文)Table 1.List of parameters(explanation present in the text).

表示分子與電極的耦合強度.分子與電極的耦合對分子電流有較強的影響,在本文中,為了強調非彈性電流效應和瞬間電流效應,設分子與電極間有弱耦合,并設隧穿現象在本文設定的弱耦合條件下不可能發生[29].當分子納米結的兩端加上電壓V時,兩端的電極化學勢發生變化分別為

3.1 分子納米結的非彈性電流

圖2 不同IVR效應下分子納米結的I-V特性曲線 黑線為光激發作用下的I-V特性曲線,灰線為沒有光激發作用下的I-V特性曲線(實線,J=0;虛線,J=1.0 meV)Fig.2.The I-V characteristic curve of molecular nanojunction for IVR effects. Black lines is the photoinduced I-V characteristic curves,gray lines is the IV curves without photoexcitation(solid lines,J=0;dashed lines,J=1.0 meV).

圖3 Rabi能為0—10 meV的條件下,IVR效應參數J=1.0 meV時,分子納米結的I-V特性曲線Fig.3. The I-V characteristic curves of molecular nano-junction for different Rabi energies and with IVR parameter of J=1.0 meV.

為了闡明外場和IVR對分子納米結I-V特性曲線的共同影響,圖3給出了ER=0—10 meV,J=1 meV條件下的I-V特性曲線.從圖中可以看到,在弱電場激發下(ER≤3 meV),Frank-Condon阻滯區域內的電流受到IVR效應的影響明顯,僅有小電流通過,隨著外加電場的升高,臺階式電流出現,說明在較強的外場作用下,IVR效應相對不明顯,電壓升高使得高能級振動態依次參與電荷轉移過程.

3.2 Gauss型外場激發作用下的瞬間電流

前面研究外場對分子納米結中I-V特性的影響時假設分子納米結在所加的外場范圍內持續受到外場的激發,實際上外場經常以脈沖形式作用在分子納米結中,在脈沖作用后分子納米結中的電流會經歷一定的響應時間才能達到穩定,在此期間左電極到分子的電流不等于分子到右電極的電流,我們稱之為瞬間電流.下面采用高斯型激光脈沖波形,研究不同脈沖寬度τs下的瞬間電流.為了突出不同偏壓對分子納米結瞬間響應特性的影響,定義電流增益函數:

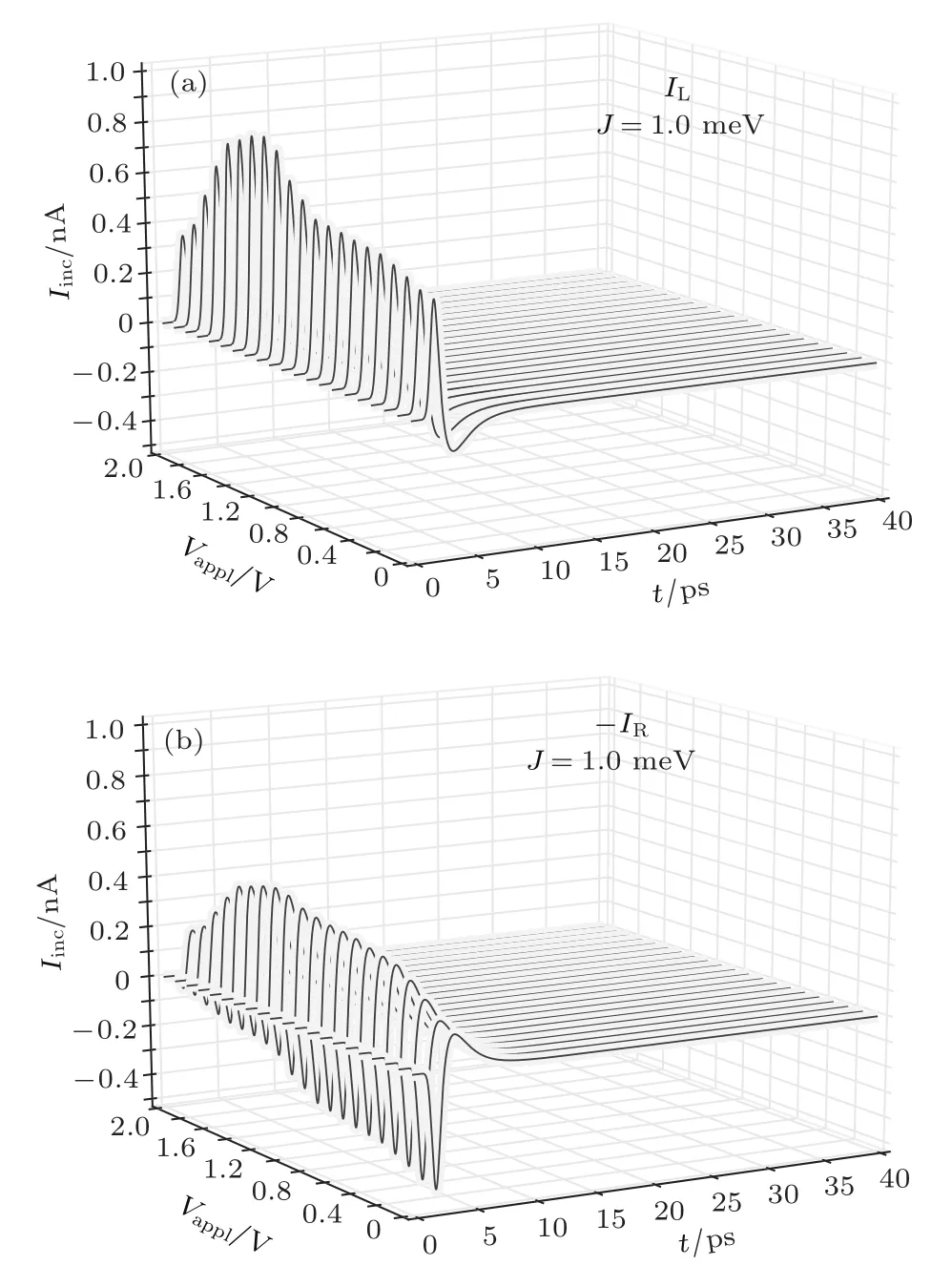
圖4 高斯型外場作用下,在偏壓范圍為0—2.0 V內,分子納米結的瞬間特性曲線 (a)左電極到分子的瞬間電流;(b)分子到右電極的瞬間電流Fig.4.Applied a Gaussian external fi eld and the bias voltage between 0–2 V,the transient I-V characteristic curves are demonstrated:(a)The transient current from left lead to molecule;(b)the transient current from the right lead to molecule.

圖4給出了不同偏壓下在脈沖寬度為ps量級的高斯型外場作用下左電極到分子的瞬間電流(圖4(a))和分子到右電極的瞬間電流(圖4(b)).比較圖4(a)和圖4(b)可以發現,隨著脈沖加入到10 ps時間范圍內電流出現瞬間行為,左電極到分子的電流呈現脈沖型增加-減少-平穩的過程,分子到右電極的電流與之相反出現減小-增加-平穩的過程.在相同的脈沖作用不同偏壓下的瞬間電流并不完全相同,在電壓較高時瞬間行為趨于平緩,但瞬間行為持續的時間大致相同.

圖5給出了脈沖寬度為0.1—10.0 ps的高斯型外場的左電極到分子的電流和分子到右電極的電流圖.當脈沖寬度較小時,瞬間電流行為不明顯,脈沖寬度在1 ps附近時,由圖5(b)可以看到,右電極向分子的逆向電流很顯著,說明在這個脈沖寬度下分子內的電子弛豫時間較長,左電極傳輸至分子的電子在分子內弛豫較長時間后才轉移至右電極.隨著脈沖寬度的增加,雖然電流增益函數也呈高斯型分布,IL與?IR幾乎同步,說明脈沖時間長,電子在被激發的同時完成了在分子中的弛豫過程,兩個過程同時進行,因此瞬間電流行為也不明顯.

圖5 在偏壓為1 V的環境下,考慮IVR效應:J=1.0 meV時,高斯型外場脈沖寬度τs的變化對分子納米結瞬間響應特性的影響,τs從前至后分別為0.1(粗),0.2,0.4,0.6,0.8,1.0(粗),2.0,4.0,6.0,8.0,10.0 ps(粗)Fig.5.With the applied bias voltage of 1 V and J=1 meV,the transient currents are plotted for various pulse widths τsof the Gaussian external fi eld.From the front to back,τsare 0.1(bold),0.2,0.4,0.6,0.8,1.0(bold),2.0,4.0,6.0,8.0,10.0(bold)respectively.

4 結 論

針對在光激發作用下由電極-分子-電極組成的分子納米結系統,考慮影響電荷輸運的幾個因素:分子與電極間的耦合、光激發作用、分子內振動態的重新分布等因素對電荷輸運過程的影響,分析了在兩個電極間加不同偏壓下的穩定電流以及不同脈沖寬度的高斯型脈沖下的瞬間電流行為.分子納米結中的穩定電流隨電壓升高呈臺階式增加,呈現非彈性特點,在光激發作用下可以有效地消除Frank-Condon阻滯.在給定的高斯型脈沖作用下,雖然在不同偏壓下瞬間電流的電流增益不同,但瞬間行為的持續時間大致相同.脈沖寬度對瞬間電流的增益也有較大影響,在脈沖寬度1 ps附近,分子內電子的弛豫時間較長,左電極電流和右電極電流出現不同步現象,在長脈沖電場激發下,電子在被激發過程中同時完成了弛豫過程,瞬間行為不明顯.

[1]Gupta C,Shannon M A,Kenis P J A 2009J.Phys.Chem.C113 4687

[2]Gupta C,Shannon M A,Kenis P J A 2009J.Phys.Chem.C113 9375

[3]van der Molen S J,Liao J,Kudernac T,Agustsson J S,Bernard L,Calame M,van Wees B J,Feringa B L,Schoanenberger C 2009Nano Lett.9 76

[4]Long M,Chen K Q,Wang L,Qing W,Zou B S,Shuai Z 2008Appl.Phys.Lett.92 215

[5]Fan Z,Chen K 2010Appl.Phys.Lett.96 053509

[6]Fan Z Q,Zhang Z H,Deng X Q,Tang G P,Chen K Q 2013Appl.Phys.Lett.102 013113

[7]Zeng J,Chen K Q 2014Appl.Phys.Lett.104 033104

[8]Yaswant V,Kumar A,Sambandan 2016Appl.Phys.Lett.109 024101

[9]Fan Z Q,Zhang Z H,Deng X Q,Tang G P,Yang C H,Sun L,Zhu H L 2016Carbon98 179

[10]Zeng J,Xie F,Chen K Q 2016Carbon98 607

[11]Ying H,Zhou W X,Chen K Q,Zhou G 2014Comp.Mater.Sci.82 33

[12]Mii T,Tikhodeev S G,Ueba H 2003Phys.Rev.B68 205406

[13]Galperin M,Nitzan A,Ratner M A 2006Phys.Rev.B73 045314

[14]Harbola U,Esposito M,Mukamel S 2006Phys.Rev.B74 4070

[15]May V,Kühn O I V 2006Chem.Phys.Lett.420 192

[16]Joachim C,Ratner M A 2005Proc.Natl.Acad.Sci.USA102 8801

[17]Qiu X H,Nazin G V,Ho W 2004Phys.Rev.Lett.92 206102

[18]Liu S,Nurbawono A,Zhang C 2015Sci.Rep.5 15386

[19]Kaun C C,Seideman T 2005Phys.Rev.Lett.94 226801

[20]Xia C J,Fang C F,Hu G C,Li D M,Liu D S,Xie S J 2007Acta Phys.Sin.56 4884(in Chinese)[夏蔡娟, 房常峰,胡貴超,李冬梅,劉德勝,解士杰 2007物理學報 56 4884]

[21]Derosa P A,Seminario J M 2001J.Phys.Chem.B105 471

[22]Emberly E G,Kirczenow G 2003Phys.Rev.Lett.91 188301

[23]Zhang C,Du M H,Cheng H P,Zhang X G,Roitberg A E 2004Phys.Rev.Lett.92 158301

[24]Pati R,Karna S P 2004Phys.Rev.B69 155419

[25]May V,Kuehn O 2008Phys.Rev.B77 115440

[26]May V,Kuehn O 2008Phys.Rev.B77 115439

[27]Wang L X,May V 2011Chem.Chem.Phys.13 8755

[28]Dulic D,van der Molen S J,Kudernac T,Jonkman H T,de Jong J J D,Bowden T N,van Esch J,Feringa B L,van Wees B J 2003Phys.Rev.Lett.91 207402

[29]Galperin M,Nitzan A 2005Phys.Rev.Lett.95 206802

[30]Flaxer E,Sneh O,Cheshnovsky O 1993Science262 2012

[31]Berndt R,Gaisch R,Gimzewski J K,Reihi B,Schlittler R R 1993Science262 1425

[32]Qiu X H,Nazin G V,Ho W 2003Science299 542