基于X射線脈沖星導航試驗衛星觀測數據的到達時間估計

，，，，，，，，，，

1. 錢學森空間技術實驗室，北京 100094 2. 中國空間技術研究院，北京 100094

脈沖星是存在于宇宙中的一種高速運轉的中子星，因自身極其穩定的周期性而被譽為宇宙中最穩定的天文時鐘，尤其是毫秒脈沖星的周期穩定度可達到10-19～10-21s/s[1，2]。X射線脈沖星導航(X-ray Pulsar-based Navigation，XPNAV)是利用脈沖星輻射的X射線進行導航[3-5]的一種新概念導航技術，它是利用X射線頻段的計時觀測數據，通過差分方程自主確定航天器的導航參數。X射線脈沖星導航系統對于未來導航系統的發展具有重要的研究意義，近年來備受國內外學者的廣泛關注[6-8]。

2016年11月10日，中國首顆X射線脈沖星導航試驗衛星-1(X-ray Pulsar-based Navigation-1,XPNAV-1)成功發射。XPNAV-1衛星工作在500 km的LEO軌道，是一顆質量為270 kg的小衛星。該衛星搭載了兩種不同體制的X射線探測器——掠入射Wolter-I聚焦型X射線探測器(簡稱Wolter-I探測器)和準直型微通道板(Microchannel Plates，MCP)探測器(簡稱MCP探測器)。XPNAV-1衛星主要任務是在軌開展X射線脈沖星的探測并進行脈沖星導航體制的驗證[9，10]。在前期的觀測中，選擇了蟹狀星云(Crab)脈沖星(PSR B0531+21)[11]進行觀測，目前已經完成了Wolter-I探測器對Crab脈沖星的多次觀測，得到了Crab脈沖星輻射的一系列的X射線光子。

在X射線脈沖星導航系統中，脈沖星的脈沖到達時間(TOA)作為導航系統的基本觀測量，其測量精度是后續的導航定位精度的決定性因素，因此對脈沖TOA進行高精度的求解是XPNAV系統中一個非常關鍵的問題[12]。多重信號子空間分類(Multiple Signal Classification，MUSIC)算法是陣列信號處理領域的一種高精度算法，主要是用于信號波達方向的估計，為了進行高精度的到達時間(Time Of Arrival，TOA)估計，本文提出了利用MUSIC方法，通過對接收數據的預處理，完成脈沖星導航系統中的TOA估計。為了驗證方法的性能，對提出的方法進行試驗仿真，即對Wolter-I探測器觀測得到的X射線光子進行了光子折疊輪廓處理得到折疊輪廓，利用本文的方法，成功得到了折疊輪廓的TOA估計值，并且估計精度與傳統互相關法相當。

1 脈沖輪廓

標準輪廓是脈沖星的一個重要特征，它是通過對脈沖星進行長時間觀測，將得到的X射線光子TOA通過光子歷元折疊方法得到的。不同脈沖星的標準脈沖輪廓不同，因此可以將脈沖星的標準脈沖輪廓作為XPNAV系統的一個必備數據。

圖1是Crab脈沖星的標準輪廓[13]，表明了Crab脈沖星的一個重要特征，它是利用長時間多次觀測的數據建立的。在XPNAV-1的觀測中，截取了一段時間內的觀測數據進行光子歷元折疊。觀測時間選為UTC 57 727.0約簡儒略日(Modified Julian Day，MJD)到UTC 57 812.0 MJD，在0.5～10 keV頻段內Wolter-I探測器共接收到4 853 983個光子，得到了119段PSR B0531+21的光子數據，將每段光子數據進行輪廓折疊[14，15]，可以得到一系列的脈沖折疊輪廓。隨機選取8段時間內光子數據進行脈沖折疊輪廓，得到圖2。

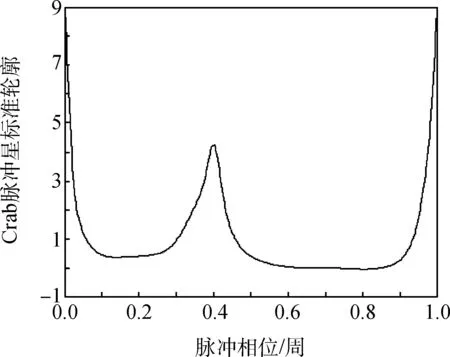
圖1 Crab脈沖星標準輪廓Fig.1 Standard profile of Crab pulsar

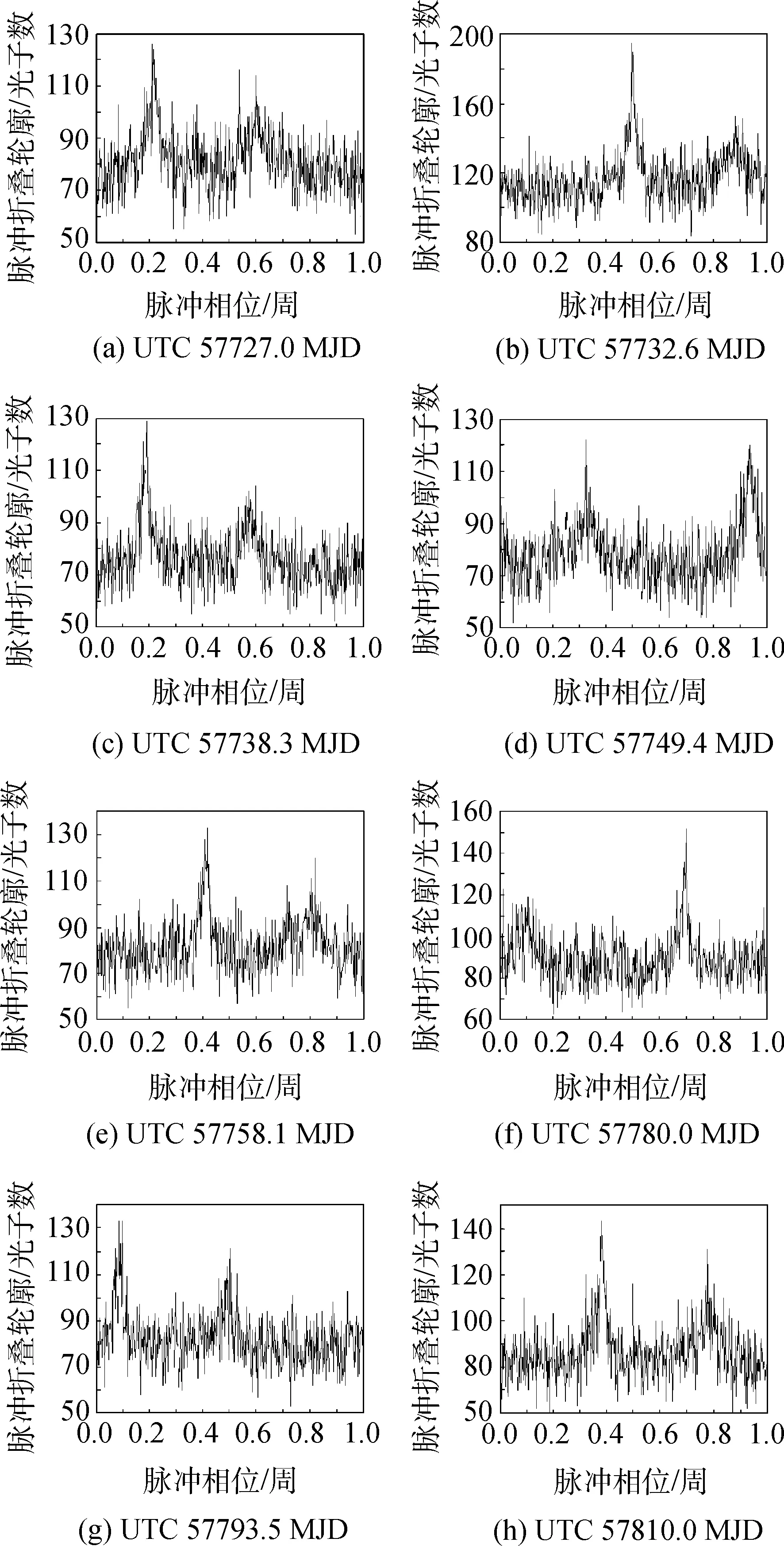
圖2 Crab脈沖星折疊輪廓Fig.2 Epoch folding profiles of Crab pulsar

對比圖1和圖2，圖2八段時間的觀測輪廓與標準脈沖輪廓形狀相同，但是在橫坐標(即脈沖相位)存在著時間的左右偏離，時間偏離值稱為脈沖TOA。脈沖TOA與相位之間的關系為TOA=φT0，T0為脈沖周期。

因此對于Crab脈沖星，可以定義其標準輪廓為s，觀測得到的折疊輪廓為r，兩者之間的關系可以建立為：

r(φi)=βs(φi-φ0)+ω(φi)

(1)

式中：β為幅度因子；φ0為r相對于s的相位偏離，即為待估計的TOA；φi(i=1,2,…,Nb)為第i個格對應的相位；Nb為在輪廓折疊過程中，將一個相位周期均勻劃分的格數；ω(φi)為等效的折疊噪聲，在折疊格中的光子數多于20個時，該噪聲可以認為是均值為零的高斯噪聲[16]。

2 脈沖TOA估計

在X射線脈沖星導航中，利用航天器上的X射線探測器探測到脈沖星X射線光子數據，通過對比脈沖星的同一個脈沖到達航天器與基準點之間的相位差，得到后續的導航參數。基準點可以設置在太陽系質心，通過脈沖星的計時觀測模型可以得到基準點的TOA，而航天器處脈沖TOA需要利用互相關法、本文方法等獲取。

2.1 互相關法

互相關法是TOA估計的常用方法，其基本原理在于對互相關函數最大值所對應的自變量的求解。

在用于XPNAV系統中進行脈沖TOA估計時，首先需要計算標準輪廓與折疊輪廓的互相關函數，即

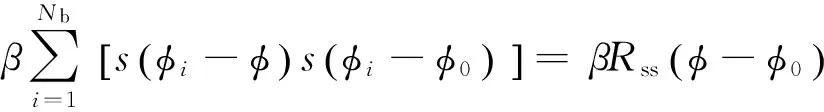
(2)

由自相關函數的性質：

|Rss(φ-φ0)|≤Rss(0)

(3)

因此，在Rsr(φ)在φ=φ0處有一個峰值，峰值對應處即為脈沖TOA的估計：

(4)

式中：arg{·}表示取函數的自變量；max[·]表示取函數的最大值。互相關函數的峰值點對應的延遲量即為脈沖TOA的估計。

2.2 本文方法

互相關法的計算簡單，但XPNAV系統中，估計精度受噪聲及信號形式的影響較大，因此針對XPNAV系統，本文提出了利用MUSIC算法對TOA進行估計。

2.2.1 MUSIC算法原理

MUSIC算法[17，18]具有“超分辨、高精度”的性能，基本原理是將接收的數據進行特征值分解，分解后得到兩個相互正交的空間，利用兩個空間的正交性計算出尖銳的譜峰，譜峰所對應的參數即為需要估計的參數。

首先可以將MUSIC算法的接收信號模型建立為：

X(t)=A(θ)S(t)+N(t)

(5)

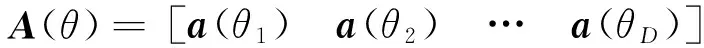
計算協方差矩陣:

R=E[XXH]=AE[SSH]AH+σ2I=

ARSAH+σ2I

(6)

對協方差矩陣進行特征值分解，可以得到特征值和對應的特征向量。將特征值由大到小排序λ1>λ2>…>λM，將特征值分為兩部分，D個較大的特征值λ1,…,λD對應著信號，相應的特征向量u1,…,uD構成了信號子空間US=[u1,…,uD]；(M-D)個較小的特征值對應著噪聲，相應的特征向量uD+1,…,uM構成了噪聲子空間UN=[uD+1,…,uM]，假設噪聲為高斯白噪聲，那么有λD+1≈…≈λM≈0。

由MUSIC算法的性質[17]可知，US與UN正交，并且導向矢量陣A(θ)與US張成了同一空間，因此有：

(7)

式(7)等號右側為一個零向量，表明陣列的導向矢量陣與噪聲子空間是相互正交的。但是在實際環境中，式(7)的右側并不是一個嚴格的零向量，而是近似為零向量。因此，MUSIC算法可以利用此性質來進行參數估計，即譜估計公式為：

(8)

最后，搜索PMUSIC(θk)的極大值點即為對應的參數值。

2.2.2 TOA估計

在波達方向(Direction-Of-Arrival，DOA)估計領域，MUSIC算法因其“高精度”性能備受學者的青睞。為了利用這個性質，本文將該算法引入到脈沖星導航系統中的TOA估計。

觀察MUSIC算法的步驟可知，MUSIC算法進行DOA估計時，利用的是同一個接收時間下的不同陣元之間的接收數據進行信號參數的估計。而利用X射線光子探測器(Wolter-I探測器)接收到的光子數據并不是同一個接收時間下的不同陣元之間的接收數據，而是在同一個陣元的不同接收時間下的光子數據，并不符合MUSIC算法的信號模型，為此需要將光子數據進行整合處理。

利用一個X射線光子探測器(Wolter-I探測器)，在不同時間下得到光子到達時間的標記，然后進行脈沖輪廓折疊，可以得到式(1)的形式，將其寫成矩陣形式為：

r= [r(φ1)r(φ2) …r(φNb)]T=

A(φ0)·β+ω

(9)

式中：r為觀測的折疊輪廓矢量；A(φ0)=[s(φ1-φ0)s(φ2-φ0)…s(φNb-φ0)]T為導向矢量，是一個與φ0(即脈沖TOA)有關的矢量；ω=[ω(φ1)ω(φ2)…ω(φNb)]T為噪聲矢量。

式(9)與式(5)具有相同的組成形式，因此可以考慮通過MUSIC算法來求解TOA。具體步驟為：

1)計算r的協方差矩陣Rr=E[rrH]；

2)對Rr進行特征值分解，UN=[u2,…,uNb]；

3)計算譜函數：

(10)

其中，搜索向量構造為：

A(φi)=[s(φ1-φi)s(φ2-φi)s(φNb-φi)]T

(11)

4)對f=[f(φ1),f(φ2),…,f(φNb)]的最大值進行搜索，最大值所對應的φk即為脈沖相位的估計，即：

(12)

3 TOA估計結果及分析

3.1 仿真及結果分析

首先對算法的有效性進行仿真，選取PSR B0531+21(即Crab脈沖星)為觀測脈沖星，Crab脈沖星的周期為0.033 1 s，背景流量為5×10-3ph/s/cm2，來自脈沖星的流量為1.54 ph/s/cm2(流量參數統計頻段為2 keV至10 keV內單位時間、單位面積探測器接收的光子數)。

(1)仿真1 TOA估計譜

選取Crab脈沖星為觀測脈沖星，探測器的面積為0.5 m2，時間分辨率為100 μs，觀測周期起點為57 727.0 MJD，觀測周期長為0.5 s，起點脈沖相位設置為φ0=0.7，分別利用互相關和本文方法進行一次脈沖相位估計，并進行歸一化處理，得到圖3。

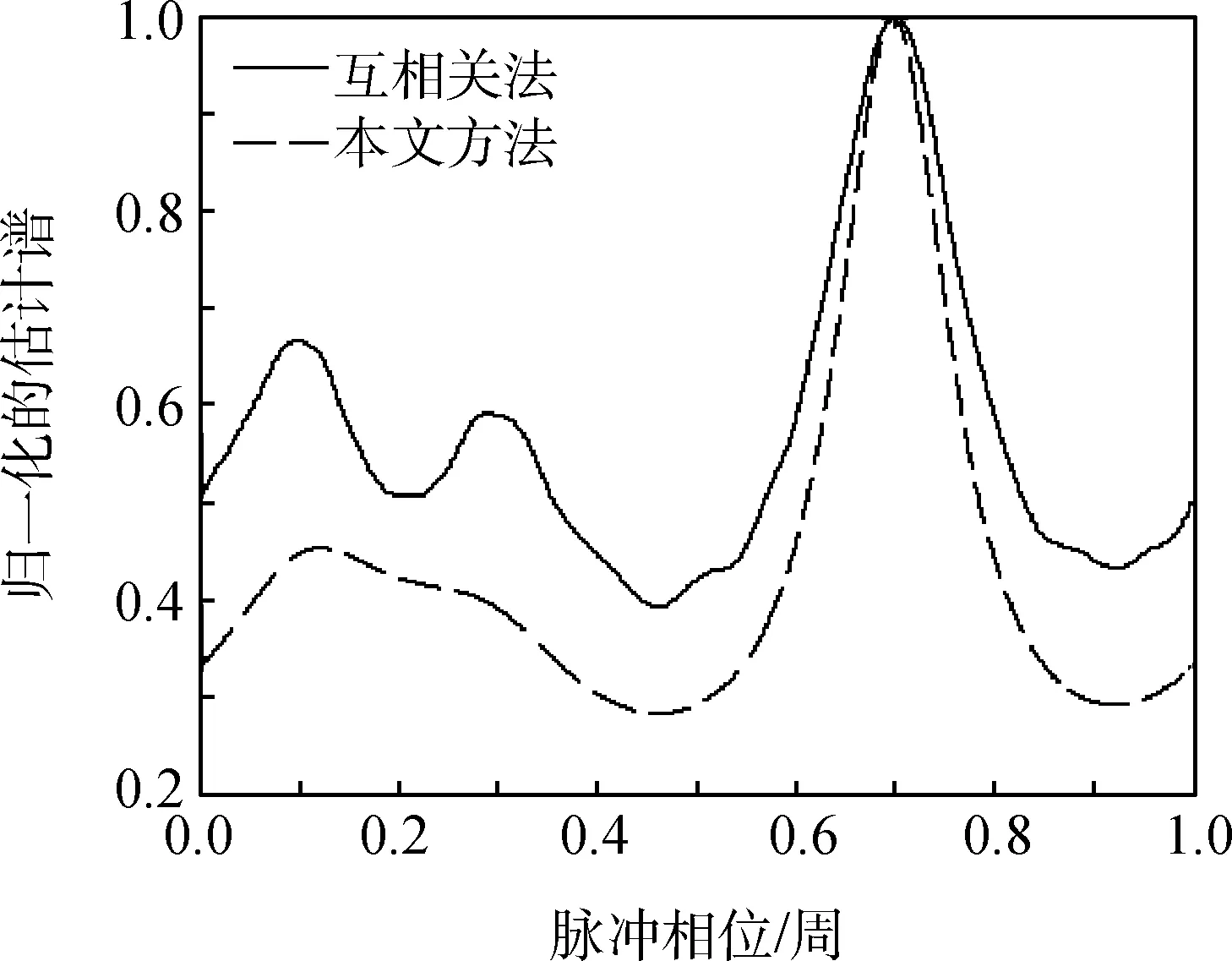
圖3 TOA估計譜Fig.3 TOA estimation spectrum

由圖3可知，本文方法的估計譜要比互相關方法的估計譜尖銳，對譜峰進行搜索，得到了互相關法與本文方法的TOA估計值分別為0.683 1和0.691 2，即本文方法的估計值較為準確。

(2)仿真2 不同觀測時間下TOA估計誤差

為了進一步驗證算法的性能，觀測時間選取0.1 s，0.2 s，0.5 s，1 s，5 s，10 s，20 s，50 s，在不同的觀測時間下分別進行100次Monte-Carlo仿真，計算TOA估計的均方根誤差，其他參數與仿真1相同。

圖4為不同觀測時間下的TOA估計誤差，可以看到，觀測時間越長，估計誤差越小，即估計精度變高，而在相同的觀測時間下，本文方法的估計精度要高于互相關法。

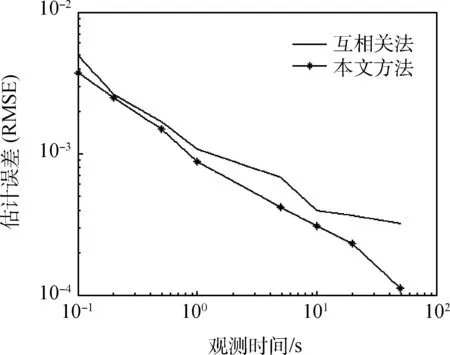
圖4 不同觀測時間下的TOA估計誤差Fig.4 RMSE in different observation time

3.2 實測數據分析

圖2是隨機選取的8段光子數據進行脈沖折疊輪廓圖，下面對這8段數據分別利用互相關法和本文方法進行脈沖相位的估計，將兩種方法得到的估計譜進行歸一化處理并進行比較，得到圖5。

由圖5可知，互相關法和本文方法均能得到TOA估計的譜峰，即兩種方法都成功進行了TOA估計。對比兩者的估計譜，可以明顯看出前者的譜峰要比后者的尖銳，因此本文算法的估計結果較為精確。

最后統計8段數據的光子數和利用兩種方法估計得到的脈沖相位，如表1所示。由表1的結果可以看出，本文方法與互相關法的估計結果相當。

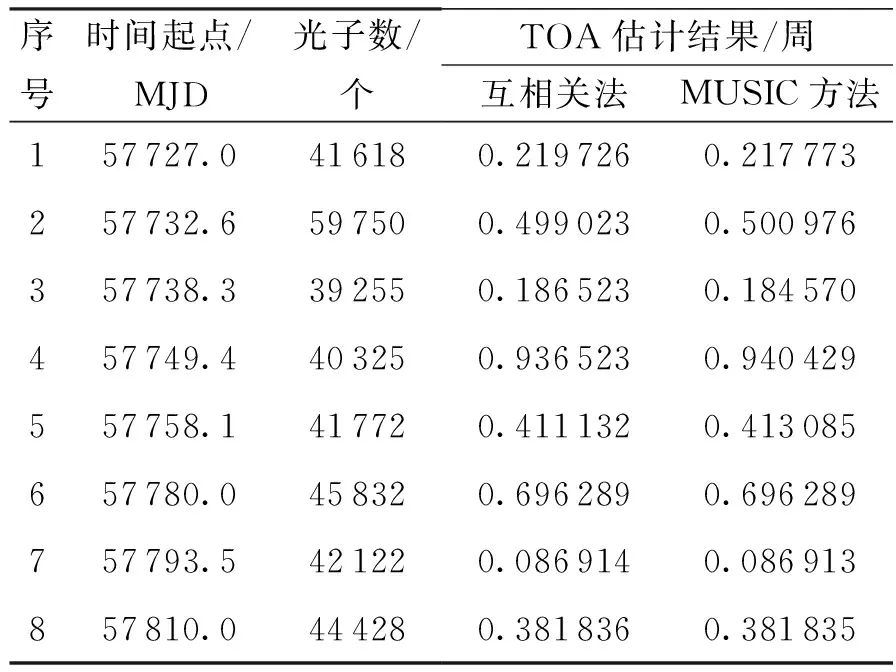
序號時間起點/MJD光子數/個TOA估計結果/周互相關法MUSIC方法157727.0416180.2197260.217773257732.6597500.4990230.500976357738.3392550.1865230.184570457749.4403250.9365230.940429557758.1417720.4111320.413085657780.0458320.6962890.696289757793.5421220.0869140.086913857810.0444280.3818360.381835

4 結束語

為了進行TOA估計，本文提出了利用MSUIC算法的高精度性質進行脈沖星導航系統中的TOA估計，并且對互相關法和本文方法進行了對比。仿真結果表明，本文方法的TOA估計的譜峰要比互相關法尖銳，在相同的情況下，本文方法的估計精度要高于互相關法。在XPNAV-1衛星前期的觀測中，選取了光子流量較強的Crab脈沖星，衛星所搭載的探測器成功接收到了Crab脈沖星的光子數據，本文中選取了57 727.0 MJD到57812.0 MJD內0.5～10 keV頻段內的光子觀測數據進行處理，得到了脈沖輪廓折疊。XPNAV-1衛星的成功發射，對建立X射線脈沖星導航系統具有突破性的意義。在XPNAV-1衛星后續的任務中，我們也規劃了對其他光子強度較弱的脈沖星的觀測。

References)

[1] 帥平.脈沖星:宇宙航行的燈塔[D]. 北京：國防工業出版社，2016.

SHUAI P. Pulsar are lighthouses for space flight[M]. Beijing： National Defense Industry Press，2016(in Chinese).

[2] HEWISH A，BELL S J，PILKINGTON D H，et al. Obser-vation of a rapidly pulsating radio source[J]. Nature，1968，217：709-713.

[3] HANSON J E. Principles of X-ray navigation[D]. CA：Stanford University，1996：1-32.

[4] SHEIKH S I. The use of variable celestial X-ray sources for spacecraft navigation[D]. MD：Maryland University，2005：375-403.

[5] 帥平，陳紹龍，吳一帆，等. X射線脈沖星導航原理[J].宇航學報，2007，28(6): 1538-1543.

SHUAI P，CHEN S L，WU Y F，et al. Navigation principles using X-ray pulsars[J]. Journal of Astronautics，2007，28(6)：1538-1543(in Chinese).

[6] The ATNF Pulsar Catalogue[EB/OL].[2017-03-17].http:∥www.atnf.csiro.au/research/pulsar/psrcat.

[7] XIONG Z，QIAO L，KIU J Y，et al. GEO satellite autonomous navigation using X-ray pulsar navigation and GNSS measurements[J]. International Journal of Innovative Computing，Information and Control，2012，8(5): 2965-2977.

[8] ANDESON K D，PINES D J. Method of pulse phase tracking for X-ray pulsar based spacecraft navigation using low flux pulsars[C]. Space Ops. Conferences，Pasadena，CA，5-9 May，2014.

[9] 黃良偉，帥平，林晴晴，等. X 射線脈沖星導航標稱數據庫構建[J].中國空間科學技術，2015，32(3)：66-74.

HUANG L W，SHUAI P，LIN Q Q，et al. Research of the nominal database for X-ray pulsar navigation[J]. Chinese Space Science andTechnology，2015，35(3)：66-74(in Chinese).

[10] 黃良偉，帥平，張新源，等. 脈沖星導航試驗衛星時間數據分析與脈沖輪廓恢復[J]. 中國空間科學技術，2017，37(3)：1-10.

HUANG L W，SHUAI P，ZHANG X Y，et al. XPNAV-1 Satellite timing data analysis and pulse profile recovery[J]. Chinese Space Science and Technology，2017，37(3)：1-10(in Chinese).

[11] WINTERNITZ L M，HASSOUNEH M，MITCELL J W，et al. X-ray navigation algorithms and testbed for SEXTANT[C]. IEEE Aerospace conference，2015:1-14.

[12] 林晴晴，帥平，黃良偉，等. 一種高精度的X射線脈沖星導航TOA估計方法[J].宇航學報，2016，37(6):604-701.

LIN Q Q，SHUAI P，HUANG L W，et al. A high precision TOA estimation method for X-ray pulsar-based navigation system[J]. Journal of Astronautic，2016，37(6):604-701(in Chinese).

[13] MPIfR EPN Pulsar Profiles Database，2017，available: http:∥rian.kharkov.ua/decameter/EPN/browser.html.

[14] EMADZADEH A A，SPEYER J L. X-ray pulsar-based relative navigation using epoch folding[J]. IEEE Transactions on Aerospace and Electronic Systems，2011，47(4): 2317-2328.

[15] EMADZADEH A A，SPEYER J L. On modeling and pulse phase estimation of X-ray pulsars[J]. IEEE Transactions on Signal Processing，2010，58(9)：4484-4495.

[16] HANSON J E，SHEIKH S I，GRAVEN P，et al. Noise analysis for X-ray navigation systems[C]. 2008 IEEE/ION Position Location and Navigation Symposium，Monterey，CA，May，2008.

[17] SCHMIDT R O. Multiple emitter location and spectrum estimation[J]. IEEE Transactions on Signal Processing，1986，34(3): 276-280.

[18] JIN H，SWAMY M N S，AHMAD M O. Efficient appli-cation of MUSIC algorithm under the coexistence of far-field and near-field sources[J]. IEEE Transactions on Signal Processing，2012，58(1): 2066-2070.