基于GPU的三維弧面漸變填充技術研究與實現

羅童心，仇建偉，王家潤

(華北計算技術研究所，北京 100083)

0 引 言

對于三維標圖軟件，線面標號繪制是其基本的功能。為使圖形符號表達更多含義，尤其在涵蓋顏色信息外還需要更直觀形象地體現某種趨勢和程度時，通常會對線面標號進行漸變填充處理，即利用兩種不同顏色的混合效果，展現諸如污染程度、進攻方向和顏色權重等信息。這種繪制效果在軌跡繪制等場合也發揮著重要作用。此外，相比于單一色彩的填充，漸變填充通常有更好的視覺效果[1-2]。

目前的三維標圖應用廣泛采用的是基于傳統圖形流水線的繪制方法，即使用固定功能的圖形流水線。該方法需要對曲面上的每個頂點綁定其對應的顏色屬性等數據，再交由圖形流水線完成余下渲染過程，其數據計算主要由CPU執行。如將該方法應用到三維場景的線面標號漸變填充中，則可能無法發揮較高的性能。這是由于為使線面標號的繪制貼合球面，通常需要填充的是細分程度較高的光滑弧面，這意味著有數量較多的頂點和三角面片數據，而在漸變填充中每個頂點的顏色不盡相同，使得CPU串行計算每個頂點的顏色值將耗費大量時間，此外為每個頂點存儲其對應的顏色屬性也需要占用大量空間[3-4]。這些問題使得圖形繪制效率較低，在復雜態勢標繪應用中無法滿足實時快速顯示的要求。

為提高三維線面標號的繪制速度，文中在固定管線渲染的基礎上使用能夠替代原有功能模塊的可編程模塊，即頂點和片元著色器，將部分原本在CPU中串行計算的大量頂點操作轉移到GPU中進行并行計算[5]。當應用于三維弧面漸變填充的場合時，該方法只需傳遞少量參數，在頂點著色器內部利用頂點位置等信息計算頂點對應顏色值，同時省去顏色屬性數組的構建和傳輸，在空間和時間性能上都有大幅度的提升。

1 算法基本概念與理論

1.1 球面的經緯映射

經緯映射是將球面上的三維笛卡爾坐標系下的點轉換為經緯度坐標的映射方式，在三維地球的標繪中通常用該映射方式取代由三維坐標系到二維坐標系的正投影或透視投影變換。

對于球心位置為原點(0,0,0)的球，球面上坐標為(x,y,z)的三維空間點轉換到經緯度坐標系的公式如下[6]：

(1)

(2)

為使弧面的漸變填充效果均勻平滑地貼合球面弧度，算法需利用球面的經緯映射將在三維地球上弧面的各頂點從三維空間坐標系映射到二維坐標系下。

1.2 漸變模型

1.2.1 關鍵參數及含義

(1)顏色混合參數：對于弧面上每個點，都對應一個顏色混合參數值，表示該位置上參與漸變的兩種顏色的混合比例，其取值范圍為0.0～1.0。根據每個頂點的顏色混合參數para，利用式(3)可以求得該位置應該被填充的顏色值。

VertexColor=(1-para)*MainColor+para*

SubColor

(3)

(2)漸變基準：可指定為弧面上任意位置，其對應的顏色混合參數為某個固定值，被作為弧面上其他點計算顏色混合參數的參照，通過弧面各個頂點到漸變基準的距離可以計算出其他位置對應的顏色混合參數。

(3)漸變半徑：即漸變基準到弧面包圍體邊界的距離，用于計算顏色混合參數。

(4)

1.2.2 輻射漸變

如圖1(a)所示，輻射漸變的漸變基準為一個點，該點的顏色混合參數為固定值0；輻射漸變的漸變半徑即為指定圓心為漸變基準的包圍圓半徑；位于包圍圓圓周上的點，其顏色混合參數均為1，其他位置的顏色混合參數則在其與漸變基準之間按距離遠近插值。輻射漸變可以直觀表達弧面上各點距離漸變基準的位置遠近，通常應用于對區域內輻射強度等信息的表達。

1.2.3 線性漸變

如圖1(b)所示，線性漸變的漸變基準是一條垂直于漸變方向的直線，該直線上所有位置的顏色混合參數均為固定值0.5；線性漸變的漸變基準到沿漸變方向的方向包圍盒兩端距離不一定相等，因此線性漸變的漸變半徑有兩個取值；在沿漸變方向包圍盒邊界，顏色混合參數為1，在與漸變方向相反的包圍盒邊界，顏色混合參數為0，其他位置的顏色混合參數則在二者與漸變基準之間按距離進行插值。線性漸變可以直觀表達弧面的方向趨勢信息以及兩種顏色參與漸變的權重，權重較大的顏色，在漸變過程中衰減得較慢，即該顏色在整個面的填充效果上占的份額較多，通常應用于行進方向等信息的表達。

圖1 兩種漸變模型及參數示意

1.3 圖形對象包圍體

1.3.1 包圍圓

對象的包圍圓定義為包含該對象的最小的圓周。在輻射漸變的漸變半徑計算中，需計算指定圓心位置的圖形對象包圍圓，即包圍圓的圓心需為漸變基準點。在確定漸變基準位置后，將所有頂點遍歷一次，計算并比較各頂點到中心位置的距離，其最長距離為指定圓心的包圍圓半徑，即輻射漸變的漸變半徑。

1.3.2 方向包圍盒

方向包圍盒(OBB)是較為常用的包圍體類型。它是包含指定繪制對象且相對于坐標軸方向任意的最小的長方體[7]。對于線性漸變的漸變半徑計算，則只需求出該圖形沿指定方向(線性漸變方向)的方向包圍盒。遍歷所有頂點，利用向量投影計算并比較各頂點到漸變基準的距離，同時運用向量的點積判斷頂點相對于漸變基準的位置，在沿兩個相反方向上的最大距離則分別為方向包圍盒的上下邊界到漸變基準的距離[8]，即為線性漸變的漸變半徑。

2 著色器

2.1 著色程序與GLSL語言

實驗使用GLSL語言編輯著色程序，實現著色器繪制，以提高渲染過程中GPU的利用率。頂點著色程序是被GPU內可編程頂點處理器執行的程序，應用程序設定的圖元信息，如頂點坐標、顏色值、法向量、紋理坐標等頂點屬性，傳入到頂點著色器中進行并行處理。存在片元著色程序時，頂點著色器的輸出會作為片元著色器的輸入，再由片元著色器的輸出決定屏幕上像素顯示的顏色，在單一使用頂點著色時，則只對輸入的頂點進行操作，頂點之間的部分則按照硬件默認的方式進行自動插值[9-11]。

GLSL是基于OpenGL的著色語言，在各顯卡上均有較好的支持，相較于僅在NVIDA顯卡上得到支持的Cg等著色語言，具有良好的可移植性[12]。GLSL語言提供了少量的內置變量和部分內置函數。

實驗中用內置變量gl_Vertex獲取頂點的三維坐標，使用transform()內置函數對頂點進行MVP矩陣變換，以及使用dot()、length()函數計算向量點積和長度等。

2.2 Uniform參數

考慮到圖形流水線的結構和著色器的并行計算能力，實驗選擇將計算每個頂點各自顏色的過程放到頂點著色器中進行，無需再額外構建和綁定頂點顏色數組。由于著色器中每個頂點的計算都是獨立在各個GPU單元間進行的，無法在獨立單元之間進行數據交換，因此涉及其他頂點的計算需要在外部程序中預先求出，再作為常量參數Uniform或頂點的屬性參數Attribute傳給著色器。

其中Uniform參數是綁定到整個著色器、用于所有頂點的參數，而Attribute參數則是綁定到每個獨立頂點的參數，通常為與頂點數組等大的數組[13-15]。為保證著色器的效率，應盡量使用Uniform傳參。

根據該算法的基本思想，對于中心漸變填充，選擇將漸變半徑和漸變基準點坐標作為Uniform常量參數傳遞給著色器；對于線性漸變填充，則將漸變半徑、中心點坐標，以及漸變方向向量作為常量參數傳遞給著色器，其中線性漸變半徑使用二維向量vec2類型以承載漸變基準兩側的半徑值。

3 算法設計與實現

3.1 繪制流程

圖2給出了基于可編程圖形管線的漸變填充繪制過程及每個計算階段的輸入輸出內容，大致可以分為在CPU中進行的預處理計算過程和在GPU中進行的計算和渲染過程。其中頂點著色器和片元著色器替代了固定管線渲染中原有的固定功能操作模塊，通過將原本在CPU中串行計算的部分轉移到著色器中進行并行計算，以提升整個計算和繪制過程的效率。

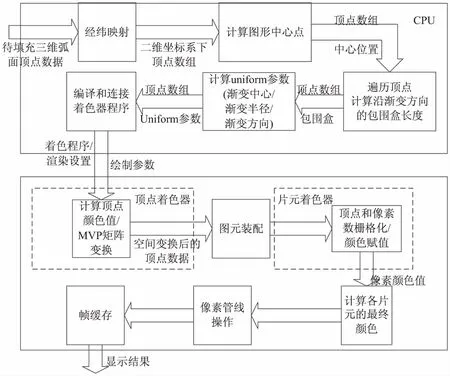
圖2 計算和繪制過程

3.2 著色程序實現

以下給出著色程序的核心代碼，用于并行計算弧面上各點顯示的顏色，分別被頂點著色器和片元著色器執行：

(1)頂點著色器。

uniform vec4 mainColor;//漸變主色

uniform vec4 subColor;//漸變輔色

uniform vec2 centerNode;//漸變基準位置

uniform vec2 radius;//兩側漸變半徑值

uniform vec2 angle;//漸變方向角度，為減少三角函數計算使用方向向量代替

varying vec4 vertexColor;//頂點顏色

floatpara;//顏色混合參數

vec2 vector=gl_Vertex.xy-centerNode.xy;//由漸變基準指向頂點的向量

float distance=dot(vector,angle)/length(angle);//頂點向量沿漸變方向向量的投影距離，大于0表示向量夾角小于90°，反之大于90°

if(distance<0.0) para=distance/radius.x;//計算顏色混合參數，向量夾角大于90°時應用左側的漸變半徑計算，反之應用右側漸變半徑計算

elsepara=distance/radius.y;

vertexColor=subColor*para+mainColor*(1-para);//計算頂點顏色

transform();//頂點MVP矩陣變換

(2)片元著色器。

varying vec4vertexColor;

gl_FragColor=vertexColor;//渲染像素顏色

4 實驗結果及分析

圖3給出了基于可編程渲染管線繪制對地球上某弧面分別進行輻射漸變和線性漸變填充的效果。AB為漸變基準位置不同的輻射漸變填充，CD為漸變方向和顏色權重不同的線性漸變填充。其中C表示漸變角度為0°，兩種顏色權重均為0.5的線性漸變填充效果；D表示漸變角度為135°，顏色權重分別為0.3和0.7的效果。AC的填充中未使用α通道。

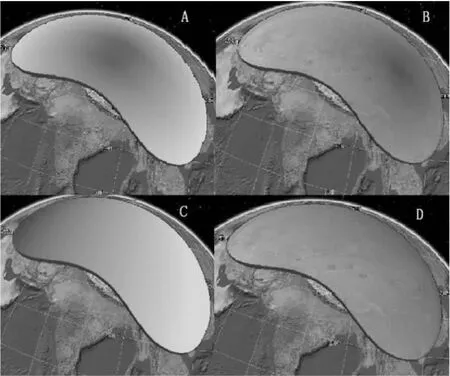
圖3 漸變填充效果

圖4給出了使用著色器渲染的實驗組與使用固定管線繪制的對照組在性能上的比對結果，分別從運行時間和顯示幀率進行對照，展示了在單一繪制對象內，隨著頂點數目和三角面片數目的增加，不同的繪制方案呈現的性能趨勢。其中實線代表實驗組的測試結果，虛線代表對照組的測試結果。測試結果統計均基于算法相對復雜的線性漸變填充。

由圖4可以看出，在三角面數量較少、網格較為簡單時，二者并未呈現較大的性能差異；當三角網格數目達到十萬級時，對照組的顯示幀率已經開始大幅降低，達到百萬級時，幀率已經下降到20幀以下，幾乎不足以支持流暢顯示；而即使三角網格數目達到100萬時，實驗組仍能保持流暢的顯示，幀率維持在30幀以上，直到數量接近200萬時才不足20幀。對照組的運行時間始終呈線性增長趨勢，實驗組運行時間則僅在數量級跨度較大時有少量的增加，在三角面數量接近200萬時，二者的運行時間差異有5倍之多。

由測試結果可以得出，使用著色器繪制的弧面漸變填充算法有著明顯的性能優勢，尤其針對繪制對象數量較少而三角面數較多的復雜線面標號，能表現出遠優于傳統固定管線繪制的性能。在渲染管線內使用著色器編程,更充分應用了GPU的計算能力，使得每個獨立的頂點計算能夠并行進行，極大地縮短了計算時間，優化了顯示效果。

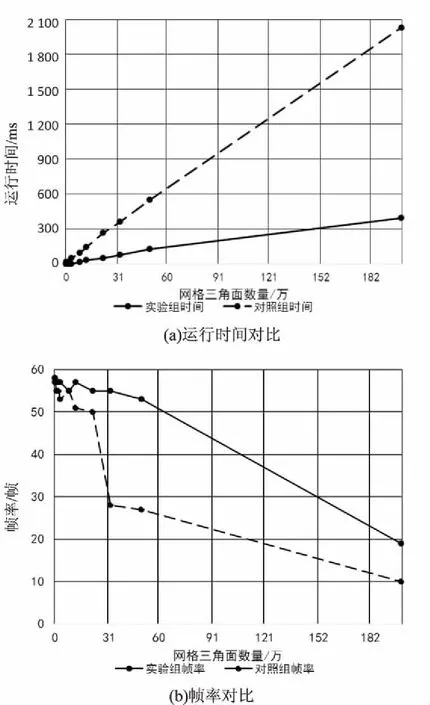
圖4 兩種繪制策略在單一繪制對象中

5 結束語

針對傳統固定管線渲染方法在沿地球弧面的三維線面標號漸變填充性能上表現出的不足，提出了基于GPU并行計算的性能優化方法。實驗結果表明，通過在渲染管線過程中使用著色器編程，提高了算法對GPU的利用率，使得對于頂點的部分計算過程能夠并行進行，極大提升了圖形的繪制效率，同時也減少了頂點部分屬性數組在空間上的占用，實現了較高性能應用于光滑弧面的兩種漸變填充效果；同時通過在線面標號漸變填充這一典型實例上的應用和大量數據測試，驗證了著色器在大量點線面數據處理上的高效率。

[1] 韓李濤，范克楠.三維地形顏色漸變渲染的光滑過渡方法研究[J].地球信息科學學報,2015,17(1):31-36.

[2] 張 旭，戴 寧，廖文和，等.基于三維漸變的牙齒磨耗可視化仿真[J].機械工程學報，2013,49(3):95-100.

[3] 簡洪登，范湘濤.基于GLSL的多重視頻紋理映射與融合[J].計算機工程與設計，2014,35(11):3873-3878.

[4] MILOSAVLJEVI? A,DIMITRIJEVI? A,RAN?I? D.GIS-augmented video surveillance[J]．International Journal of Geographical Information Science,2010,24(9):1415-1433.

[5] 裘 初，費廣正，石民勇.可編程圖形硬件綜述[J].北京廣播學院學報：自然科學版，2004,11(3):13-19．

[6] 王俊杰，徐小剛，胡運發，等.魚眼投影在虛擬實景中的應用研究[J].小型微型計算機系統,2004,25(2):287-290.

[7] 蘆鴻雁.基于層次包圍盒的碰撞檢測算法研究[J].計算機與數字工程,2008,36(2):23-25.

[8] 李運鋒，劉修國.基于方向包圍盒投影轉換的輪廓線拼接算法[J].計算機應用，2011,31(12):3353-3356．

[9] CIRNE M V M,PEDRINI H.Marching cubes technique for volumetric visualization accelerated with graphics processing units[J].Journal of the Brazilian Computer Society,2013,19(3):223-233.

[10] WATSON B,LUEBKE D.The ultimate display:where will all the pixels come from[J].Computer,2005,38(8):54-61.

[11] 韓俊剛，蔣 林，杜慧敏,等.一種圖形加速器和著色器的體系結構[J].計算機輔助設計與圖形學學報，2010，22(3):363-372.

[12] 黃 龍.基于GLSL三維渲染效果的研究與應用[D].西安:西安科技大學，2014.

[13] WOO J H,SOHN J H,KIM H,et al.A 195 mW,9.1M vertices/s fully programmable 3-D graphics processor for low power mobile devices[J].IEEE Journal of Solid-State Circuits,2008,43(11):2370-2380.

[14] 陳繼選，王毅剛.基于OSG的GLSL著色器編輯環境[J].計算機系統應用，2011,20(3):153-156.

[15] WOLF D.OpenGL4.0 shading language cookbook[M].[s.l.]:PACKT Publishing,2011.