地鐵區間隧道風速監測點選取分析研究

王方宇 畢海權 王宏林 曹 松

?

地鐵區間隧道風速監測點選取分析研究

王方宇 畢海權 王宏林 曹 松

（西南交通大學機械工程學院 成都 610031）

為了確定地鐵區間隧道內的平均風速，合理布置風速監測點是準確監測斷面平均風速的關鍵。針對圓形地鐵區間隧道，對隧道內活塞風速大小和斷面上風速分布進行了數值研究，研究結果表明區間隧道內的活塞風速大小為2m/s～10m/s；通過將監測點布置在平均風速點處直接測得隧道平均風速的方法是不可行的，而通過修正監測點風速得到隧道內的平均風速的監測方法是可行的，并給出了隧道斷面上不同監測點處風速與斷面平均風速的計算公式；隧道內監測點風速與隧道平均風速呈線性關系，且監測點離隧道中心越近，線性關系的相關性越高。

地鐵區間隧道；風速監測點；平均風速；風速分布；數值計算

0 前言

地鐵隧道內的風速大小和分布是決定隧道內是否擁有一個良好環境的重要因素[1]，為保證隧道內合理的風環境，有必要對地鐵隧道內風速進行長期監測。由于隧道環境十分復雜，風速監測點位置的選取是準確監測風速的關鍵，監測點的選取原則包括兩方面，一是該位置點處的風速能夠直接或者間接反應出隧道平均風速，二是監測處布置的傳感器不能越過車輛限界，避免其對行車安全造成影響。

現有對于列車活塞風的研究主要集中在活塞風特性、活塞風的影響因素以及隧道內通風方案的優化[2-6]，對隧道斷面上風速分布規律的研究很少。國內外關于地鐵隧道風速的監測點選取的研究幾乎空白，僅有對地鐵活塞風測試的相關研究。以往研究人員在進行地鐵隧道風速測試時，常用的測試方法是在隧道兩側布置若干個測點，或采用人工手持測試的辦法在多個位置進行測試。但由于實際隧道內的風速并不均勻，上述多點布置的方法不僅會大大增加監測系統建設成本，而且還會增加測試儀器安裝和維護的難度，因此目前隧道風速測點的選取方法并不合理，不能直接用于風速監測。本文采用數值計算方法分析了區間隧道的活塞風速大小變化范圍和斷面上風速分布特性，并研究了圓形區間隧道斷面上風速監測點選取方法的可行性。

1 數值計算方法

1.1 計算模型

本文重點研究圓形盾構地鐵區間隧道，計算模型參照重慶某軌道交通線區間隧道，并對隧道內部管線等凸起結構進行了適當簡化，如圖1、圖2所示。

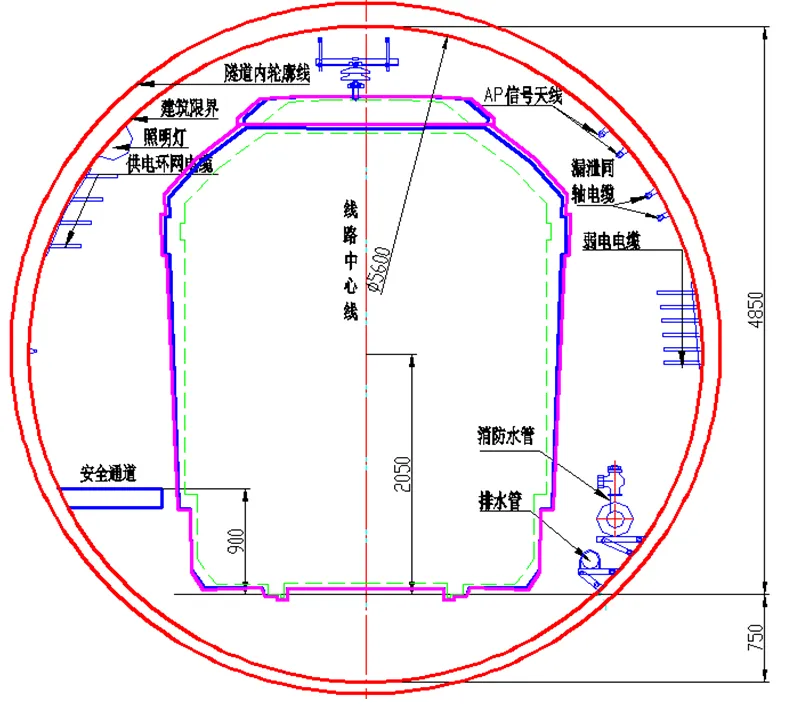
圖1 區間隧道內部結構示意圖

圖2 區間隧道計算模型

數值計算中隧道長度為500m，圓形區間隧道的斷面直徑分別為5.2m、5.4m、5.6m、5.8m、6.0m。

計算模型采用多面體網格進行劃分，五種尺寸隧道模型的網格單元數量約為690萬～970萬。

1.2 邊界條件和求解條件

隧道模型包括一個風流入口和一個風流出口，風流入口設置為速度入口，風流出口設置為壓力出口，隧道壁面設置為固定壁面。隧道壁面的襯砌粗糙高度取0.0089m，軌面的粗糙高度取0.0095m。

計算中假定隧道壁面與空氣無熱交換，且隧道內無質量源輸入，隧道內的空氣流動視為粘性不可壓縮流動。模擬計算時采用單精度的分離式求解器，湍流模型選用Realizable湍流模型。

1.3 計算方法驗證

隧道內空氣流動屬于非圓管的三維不可壓縮湍流流動，其流動物理特性與標準圓管內的湍流流動相似，因此本文研究了入口風速6m/s，內徑分別為5.2m、5.4m、5.6m、5.8m和6.0m標準圓管內湍流運動研究，將得到的充分發展段斷面上的平均風速點到壁面距離值和最大速度值與湍流充分發展段速度分布半經驗公式[14-16]的計算值相比較，公式如下：

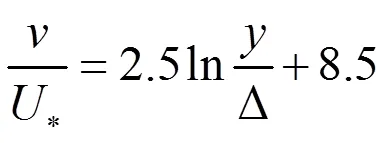
其中，為圓管內某點的速度，為該點到管壁的距離，壁面的粗糙高度是Δ，*為摩擦速度。

驗證計算模型和計算方法的可靠性，對比結果如圖3所示。由圖可見兩種計算結果的變化趨勢一致，且誤差在5%以內。因此本文針對隧道內的速度分布采用的數值計算方法是準確的。

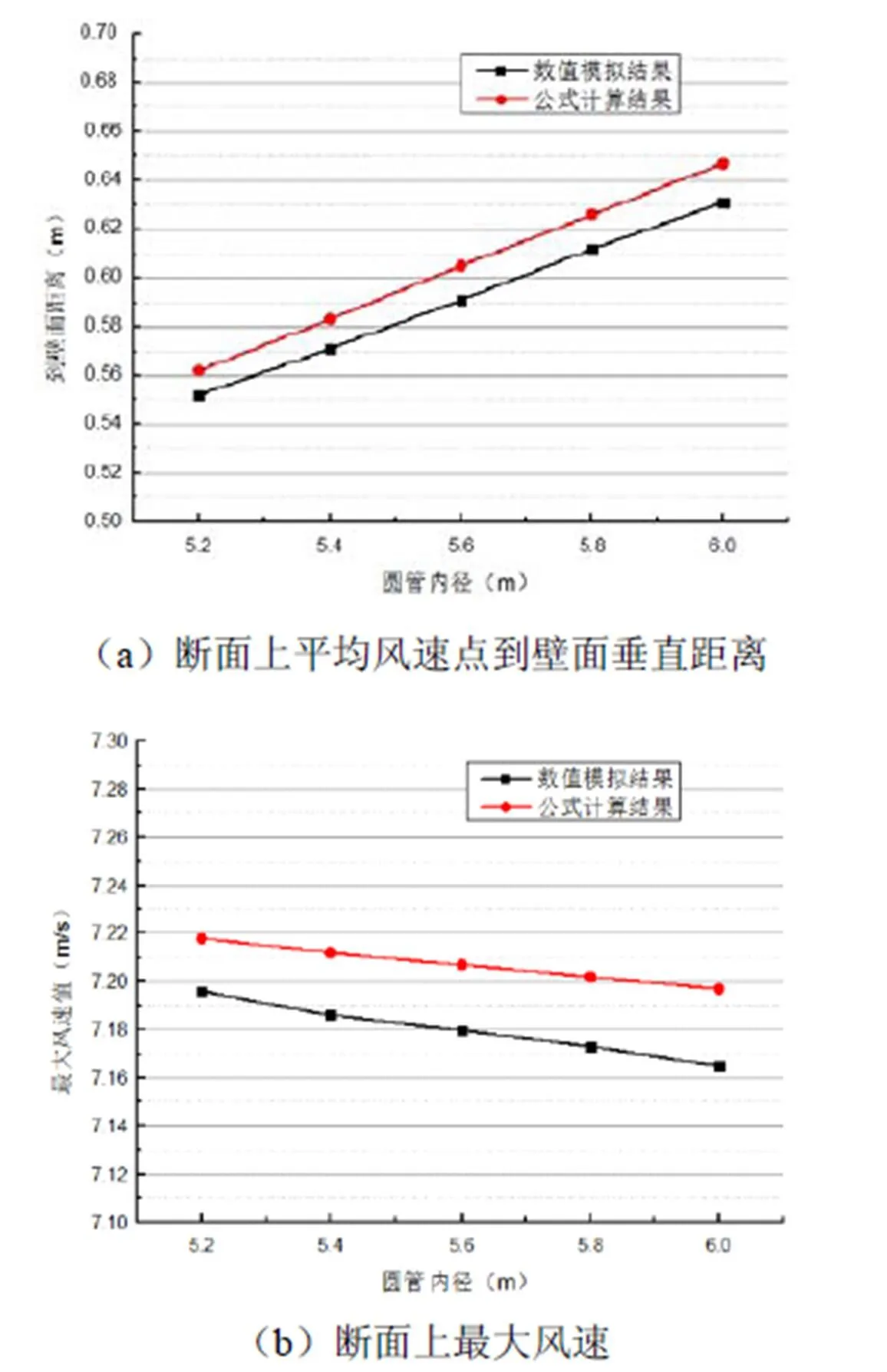
圖3 數值計算與公式計算結果對比

2 區間隧道內活塞風速范圍的確定

以重慶某軌道交通線為研究基礎，選取其中一個典型的地下車站及與其相連的區間隧道，根據該軌道交通線路的設計參數確定了8個車站相連的單線隧道一維計算模型，如圖4所示。模型線路全長為10.6km，車站隧道的長度為140m，斷面積為20.545m2；車站站臺端至區間隧道之間的過渡段隧道長30m，斷面積為29m2；兩站之間的區間隧道長取1km，斷面積為23.32m2；活塞風井高度為20m，格柵自由面積為16m2；隧道考慮為直線，坡度考慮為0。

圖4 隧道一維計算模型網絡節點圖

地鐵列車選用A型車，車體正面投影面積為11.45m2，長度為122m，最高運行速度為80km/h。列車平均加速度及列車平均減速度均為0.62m/s2。行車對數為30對/h。

利用SES軟件對多列地鐵列車在整條線路上的運行進行動態模擬一段時間后，截取D站停靠的列車即將發車的時刻，從該時刻開始，逐秒計算該列車從D站開始起步直至抵達前方車站E的過程中區間隧道內的風速大小變化。同時建立與D站、E站以及兩站間區間隧道相對應的三維計算模型，計算與一維數值計算相同過程中活塞風的變化。

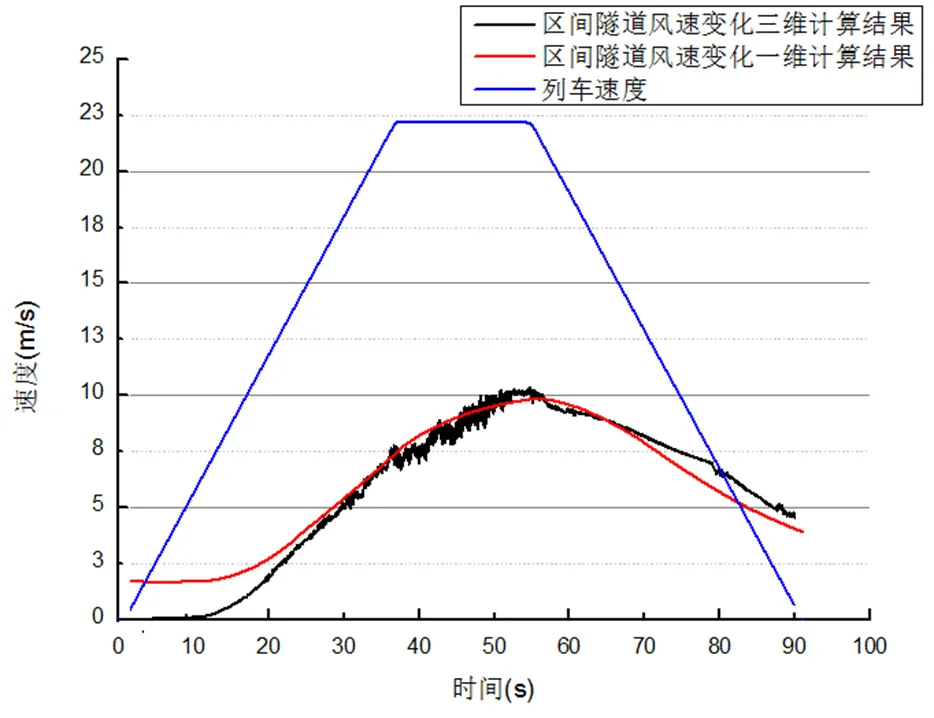
圖5 計算結果對比

圖5為一維和三維計算模型得到的區間隧道活塞風速，由圖可見兩種計算得到的活塞風速曲線吻合良好。此外計算結果還表明區間隧道內活塞風速與列車速度的變化規律基本一致，且區間隧道內活塞風速大小變化范圍大致為1.74m/s～9.84m/s。

通過以上計算結果，針對區間隧道內的測點選取進行研究時，考慮的隧道內平均風速范圍為2m/s～10m/s。

3 風速監測點位置選取的研究分析

根據第2節確定的區間隧道風速范圍，分別研究風速入口平均風速分別為2m/s、4m/s、6m/s、8m/s及10m/s工況下，湍流充分發展段內距風速入口400m的隧道斷面上的風速分布。本文擬通過兩種思路來對風速監測點的位置選取進行分析研究，第一種基于布置一個風速測點，使該點所測得的風速值能直接反映出隧道內的平均風速，第二種給定一個函數關系，通過修正監測結果從而得到隧道平均風速。

風速監測點位置選取的首要原則是不影響列車行車安全性，其次應該避開斷面上線等結構產生的渦流區的影響，另外還需兼顧安裝維護方便，以保證能夠長期獲得出準確可靠的數據。通過以上分析可知，相對比較合適布置風速監測點的位置區域只有圖6中的區域1和區域2。為了便于分析對比，對區域1與隧道斷面圓心平齊的高度直線和區域2過隧道斷面圓心與水平線成45度夾角的直線上的點進行研究，測點具體位置如圖6所示。

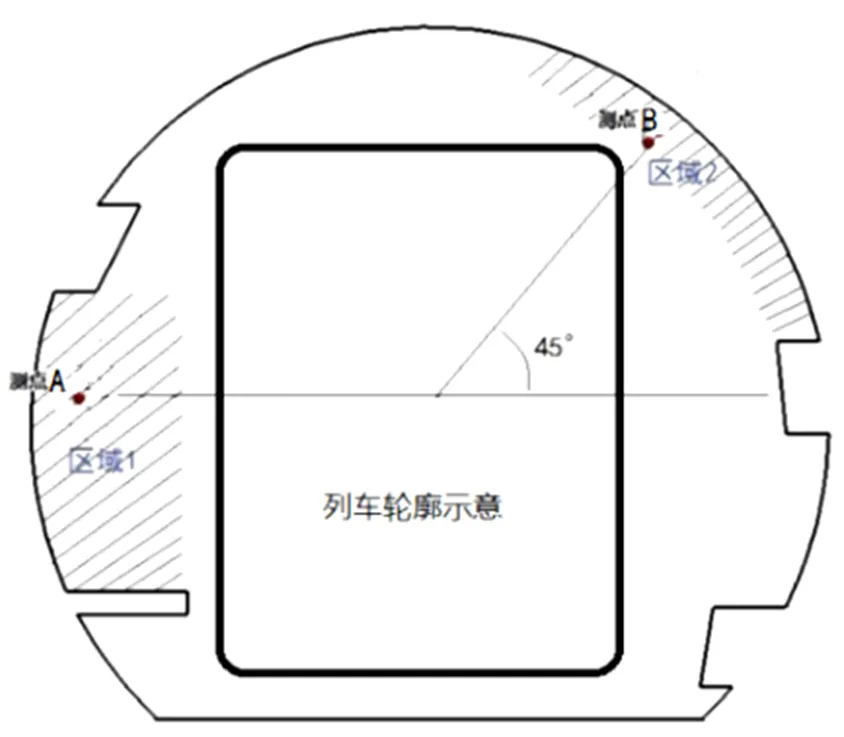
圖6 監測點位置選取示意

3.1 基于平均風速點監測方法的研究

由表1和表2中計算結果可知，當隧道內平均風速相同時，平均風速點到隧道壁面的距離隨著隧道直徑增大而增大；對于同一直徑尺寸的隧道，當隧道內的風速增大時，由于隧道本身圓缺形狀和安全通道，管線等凸起結構造成隧道斷面上的各向非同性，從而導致平均風速點與隧道壁面的距離隨著平均風速的增大而減小，這與相應圓管規律不一致。

由上可見對于同一區間隧道，平均風速點的位置會隨平均風速的改變而改變，且平均風速點離壁面的距離基本上都大于0.5m，在該位置布置監測點會影響安全通道上人員通行和列車的行車安全，因此將監測點布置在隧道斷面上平均風速點的位置來監測隧道平均風速的方法是不可行的。

3.2 基于修正風速監測值監測方法的研究

在圖6中區域1和區域2的直線上，離壁面垂直距離為200mm和300mm的地方，分別選定風速監測點A1、A2、B1和B2。表3顯示了各工況下四個監測點的風速值。對表中數據進行分析可知，監測點風速隨平均風速的變化大致呈線性。由于受篇幅限制，本文僅給出了5.6m直徑隧道的監測點風速變化曲線圖，如圖7所示。

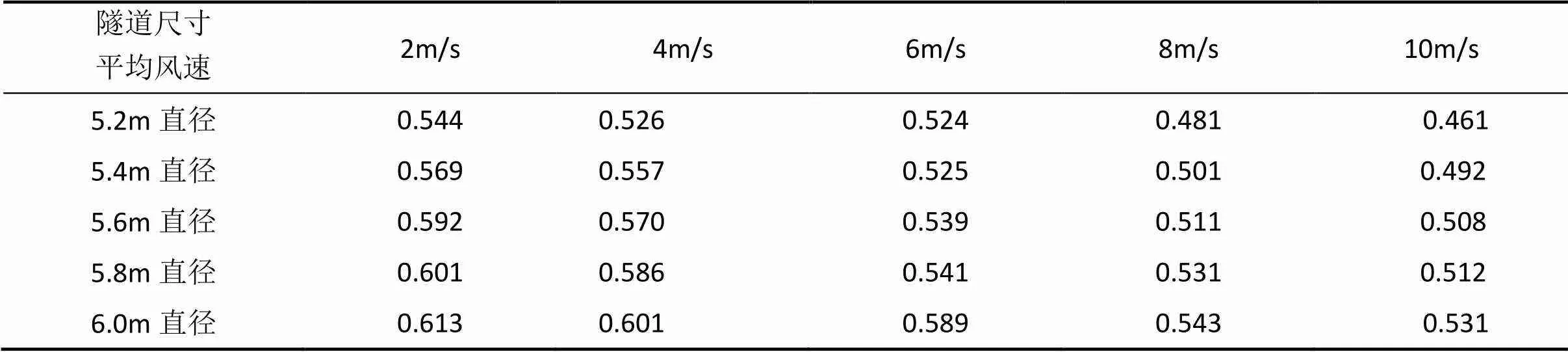
表1 平均風速點A離隧道壁面垂直距離（單位：m）

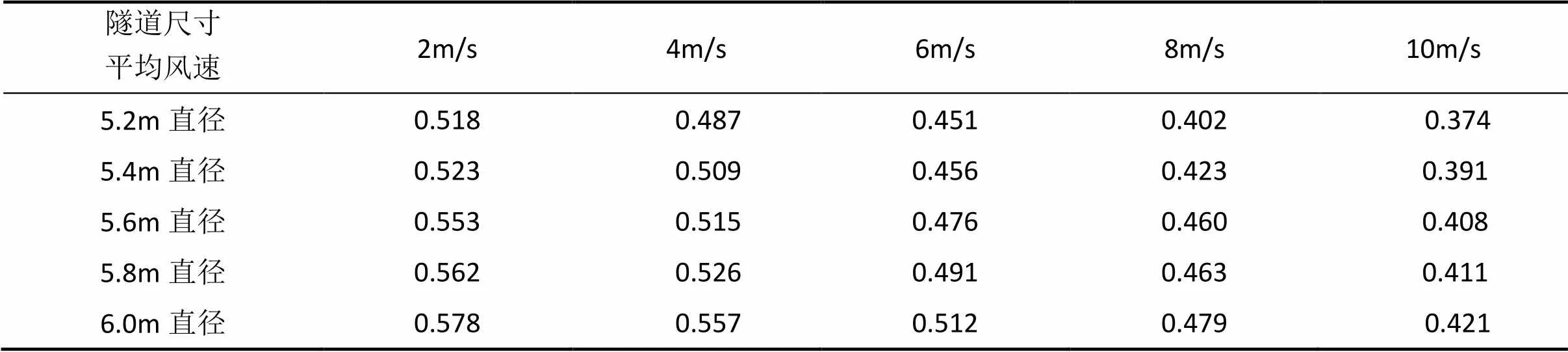
表2 平均風速點B離隧道壁面垂直距離（單位：m）

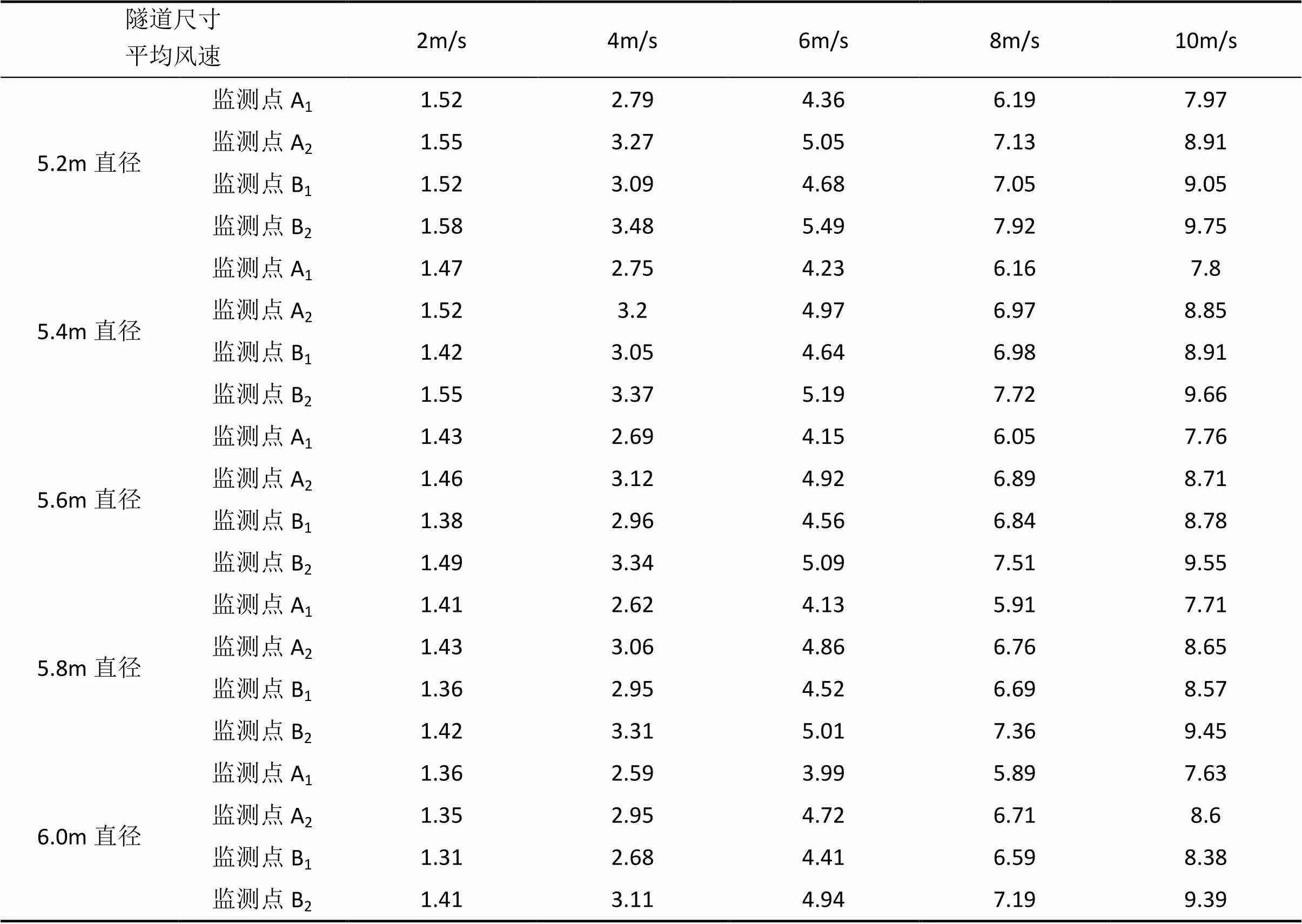
表3 風速監測點風速值（單位：m/s）

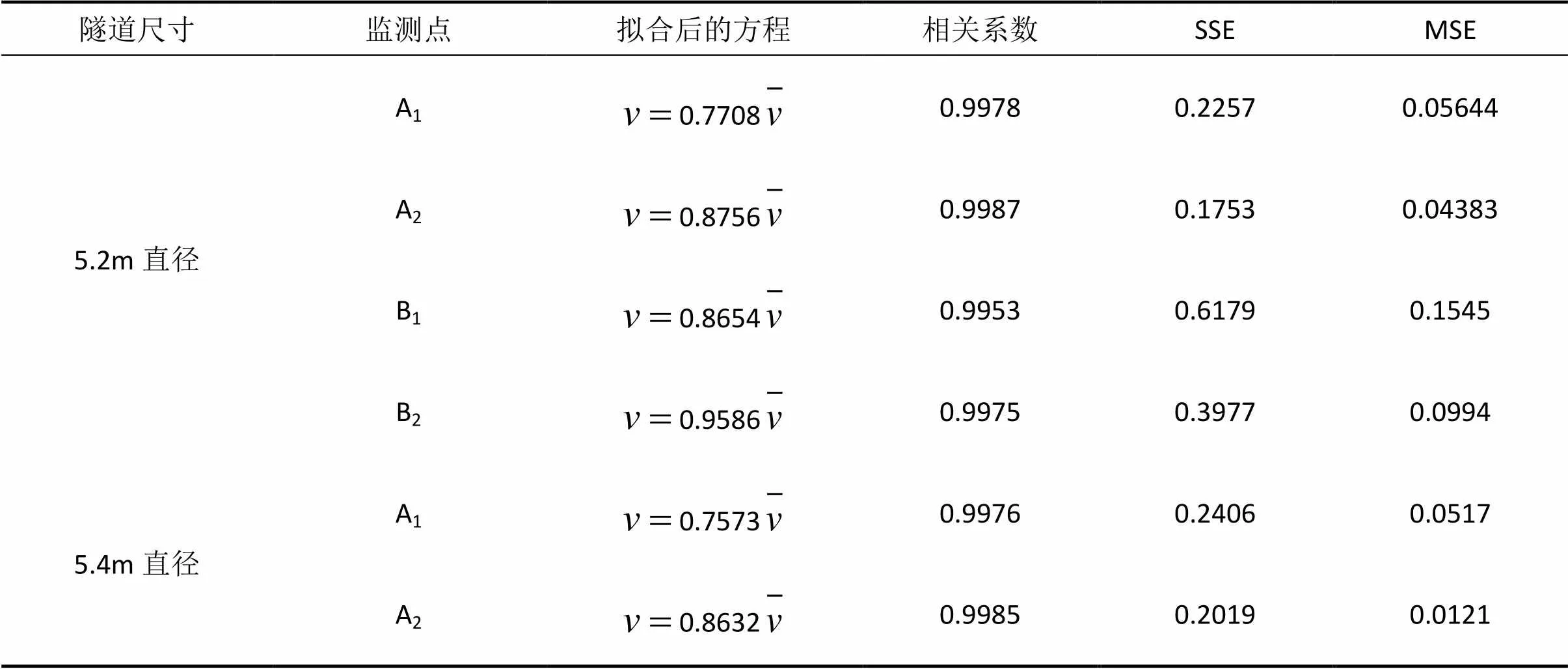
表4 不同直徑隧道各監測點風速擬合方程

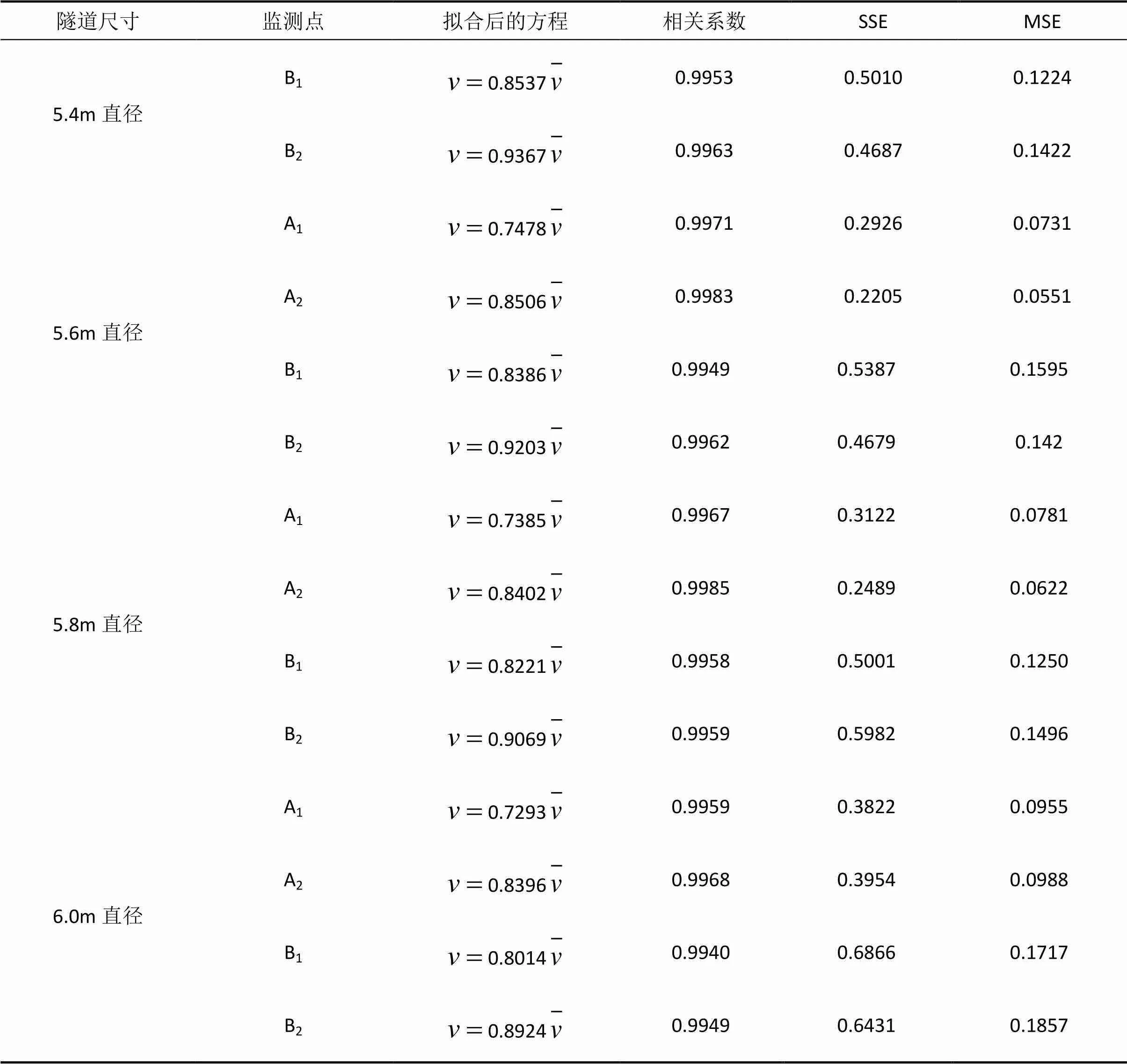
續表4 不同直徑隧道各監測點風速擬合方程

4 結論

（1）地鐵區間隧道內的活塞風速一般在2m/s～10m/s之間。

（2）由于受車輛限界的限制，將地鐵區間隧道風速監測點布置在斷面平均風速點位置直接測得隧道平均風速的方法是不可行的。

（3）在隧道靠近壁面較空曠且不影響地鐵列車行駛安全的區域布置風速監測點，通過修正監測點風速得到隧道內的平均風速，從而對區間隧道內平均風速進行監測方法是可行的。

（4）隧道內監測點風速與隧道平均風速呈線性關系，且監測點離隧道中心越近，線性關系的相關性越高。

[1] 吳喜平.地鐵與熱環境[J].能源技術,1999,(4):37-39.

[2] Ming-TsunKe, Tsung-CheCheng, Wen-Por Wang. Numerical simulation for optimizing the design of subway environment control system[J]. Building and Environment, 2002,37(8):1139-1152.

[3] 王麗慧.地鐵活塞風與地鐵環控節能[D].上海:同濟大學,2007.

[4] 豆鵬亮.地鐵活塞風與新型屏蔽門環控系統的數值研究[D].上海:東華大學,2013.

[5] 趙蕾,王君,胡浩明,等.基于實測的西安地鐵二號線活塞風特性分析[C].2014年鐵路暖通年會,2014.

[6] 王樹剛,江億,朱穎心.北京地鐵列車活塞風的實測與分析[J].暖通空調,1998,(5):47-49.

[7] 郝元偉,陳開巖,蔣中承,等.基于CFD模擬的港道風速監測值修正處理[J].煤炭安全,2011,42(2):1-3.

[8] 王翰鋒.基于Fluent巷道斷面平均風速點定位監測模擬研究[J].煤炭科學技術,2015,43(8):92-96.

[9] 暨朝頌.管流中湍流速度分布函數[J].中國礦山工程,2013,42(4:63-67.

[10]魯華偉,畢海權,周陽,等.高緯度寒區隧道施工熱環境數值計算研究[J].制冷與空調,2016,30(2):2015-207.

Study on the Selection of Air Velocity Monitoring Point for Circular Subway Interval Tunnel

Wang Fangyu Bi Haiquan Wang Honglin Cao Song

( School of mechanical engineering, southwest Jiaotong university, Chengdu, 610031 )

In order to determine the reasonable air velocity monitoring point layout position of average air velocity monitoring in the circular subway interval tunnel, the numerical simulation method is used to analyze the size of velocity and distribution of air velocity in the cross section in the tunnel. The result show piston wind speed in the interval tunnel is 2m/s～10m/s. It is feasible to install the air velocity monitoring point in the area close to the wall and does not affect the safety train, and obtain the average air velocity in the tunnel by modifying the air velocity of the monitoring point. At the same time, the relationshipbetween the air velocity at the monitoring point and the tunnel diameter and the average air velocity is summarized. The air velocity of monitoring point is linearly related to the average air velocity in the tunnel l, and the monitoring point is closer t to the center of the tunnel, the linear correlation is higher.

Subway interval tunnel; air velocity monitoring point; Average air velocity; distribution of air velocity; numerical calcucation

1671-6612（2018）01-071-07

TU834/U231.5

A

王方宇（1990.3-），男，在讀碩士研究生，E-mail：wfangyu123@163.com

畢海權（1974.12-），男，教授，E-mail：bhquan@163.com

2017-06-01