MArP風險過程破產時間的改進算法
溫玉卓,唐勝達,鄧國和
(廣西師范大學a.經濟管理學院;b.數學科學學院,廣西桂林541004)
0 引言
定義MArP風險過程:

其中,u是初始盈余資金,常數c>0是保費率。不妨設c=1,設J={}J(t),t≥0是不可約連續時間Markov過程(CTMC),稱J為環境過程。J的有限狀態空間為EJ={1,2,…,M},狀態i∈EJ表示保險公司所處的風險環境。計數過程N(J(t))表示風險過程在(0,t]的索賠次數。設{(J(t),N(J(t))),t≥0}構成一Markov到達過程[1](Markov Arrival Process,MArP)。具體地,在狀態空間EJ×N上存在兩個M階矩陣,滿足:
①Q(0)+Q(1)構成環境過程J的轉移率矩陣;
②對所有j,k∈EJ,j≠k,qjk(0)≥0表示環境狀態由j轉移至k時,沒有索賠發生的轉移速率;
③對所有j,k∈EJ,qjk(1)≥0表示環境狀態由j轉移至k時,發生索賠的轉移速率。
在風險過程(1)中,Xi表示風險過程的第i次索賠大小。給定環境狀態時,設索賠序列{Xi}相互獨立。本文假定索賠Xi具有PH分布,由于PH分布對于一切具有正支撐分布類稠密[2],因而這一假設使得索賠更具一般性及概括性。設索賠受環境過程J影響,即當環境狀態由j轉移至k并發生索賠時,險種索賠額的分布為PH(βk,Bk),記bk=-Bke,其中e是維數適當的單位列向量,不失一般性,對所有k∈EJ,設PH(βk,Bk)對應的潛在Markov過程的瞬間狀態空間為Eph={1,2,…,K}。本文總是假定風險過程(1)滿足正的安全負荷條件:

其中μk=-βkBk-1e表示在k狀態發生索賠額的期望,{πj,j∈EJ}是環境過程J的平穩分布,即
本文主要討論MArP風險過程(1)的與破產時間相關的性能指標。基于此,定義:

稱τ為風險過程(1)的破產時刻。若對任意i∈Em1,都有V(t)>0,則令u,0)。

定義破產時刻τ的分布函數為:定義破產時刻τ的Laplace-stieltjes變換(LST):
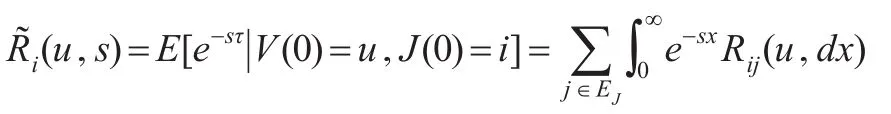
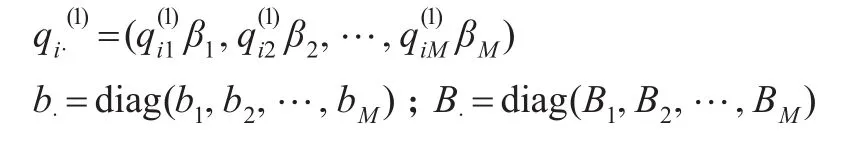
1 模型分析
Markov流體隊列(MFQ)最初源于網絡通訊,它在近二十年得到了迅速發展,已被成功應用于網絡通訊、供應鏈、火災防控、風險理論等領域。下面對本文需要用到的MFQ理論進行簡單介紹。
1.1 MFQ的忙期
設{(Y,φ)}={(Y(t),φ(t)),t≥0}是二維隨機過程,其中,過程φ是空間為E,轉移率矩陣為T的CTMC,稱φ={φ(t),t≥0}為背景過程,Y={Y(t),t≥0}稱為水平過程,過程Y的變化滿足如下等式:于是,稱為Markov流體隊列(MFQ)。

稱ci,i∈EJ為純輸入率,本文設ci只取值正負兩種情況,對狀態空間分類E=E+∪E-,其中,E+={i∈E,ci>0},E-={i∈E,ci<0},定義矩陣C+=diag{ci,i∈E+},C-=diag{-ci,i∈E-},C=diag(C+,C-)。對應于E=E+∪E-,轉移率矩陣T可寫成如下分塊形式:

下面定義首達時(first passage time,FPT):

其中,θ表示初始水平為u的隨機流體隊列首次回到初始水平u的時間。顯然,θ與流體隊列的初始水平無關。χ表示初始水平為u的隨機流體隊列首次達到水平0的時間。記θ與χ相應的分布函數為:
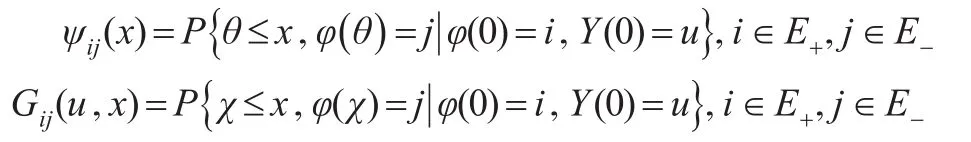
記矩陣ψ(x)=(ψij(x)),G+-(u,x)=(Gij(u,x))。記θ與χ相應的LST變換為:
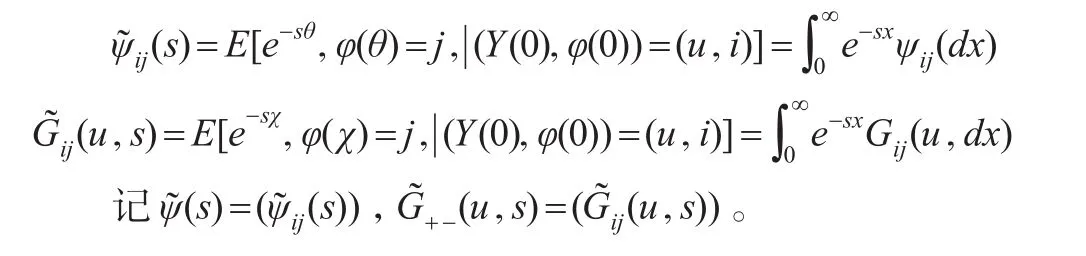
由文獻[3],有如下引理成立:
引理1:對MFQ{}(Y,φ)有如下等式成立:

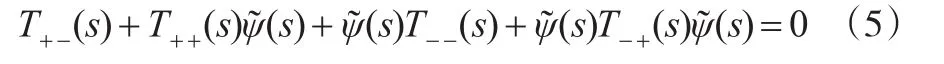
對于上Riccati方程,由L-R算法[3]可求解(s)。
1.2 模型轉換
本文基于Asmussen[4]和張超權[5]等的方法,提出一種新的改進算法,稱為Erlang逼近算法,不同于Asmussen[4]和張超權[5]將風險過程(1)轉化與之具有相同演變規律的MFQ模型,本文中,風險過程(1)轉化為初始水平為0的MFQ模型序列。使得MFQ模型序列逼近具有相同演變規律的MFQ模型,本文提出的這一改進算法的優點在于,Erlang逼近算法保持了原方法的優點,同時,這一算法的所有指標量的討論都限定在一個忙期內,即求解過程中只涉及一個指標量(忙期)的計算,同時,Erlang逼近算法較之文獻[5-8],這一轉換關系回避了MFQ模型的流體水平過程的各種演變情況的分類及討論,使得計算程序十分簡潔,而且算法概率意義直觀,同時,對于Asmussen等的方法不可能討論的量,如MFQ模型最值的分布等,也可以應用這一方法進行求解。下面將詳細介紹這一方法。

圖1 風險過程樣本路徑

圖2 風險過程對應的MFQ模型樣本路徑
首先,如圖1和圖2所示,假定風險過程(1)在發生索賠時,并非一次性付清,而是以速率1連續支付,直至付清。于是風險過程(1)轉化為MFQ模型(t)),t≥0},見圖2。其中,環境過程(t)的狀態空間為,記為過程的初始分布向量。類似于文獻[3,6,9],根據背景過程的轉移特點,得到相應的轉移率矩陣,其中,構造如表1所示,表中的第一列表示初始狀態i,第二列表示轉移狀態j,第三列表示對應的轉移率,i≠j,轉移率矩陣元素可以根據轉移率矩陣行和為0這一性質得到。
表1 過程的轉移率矩陣的元素結構

表1 過程的轉移率矩陣的元素結構
初始狀態i i(i,j,l)(i,j,l)i其他轉移狀態j 轉移率j1j q(0)ij Bj(l,ν)bj(l)(i,j,l)其他q(1)ijβj(l)0備注i,j∈EJ,l,ν∈Eph,k=1,2,…,M.
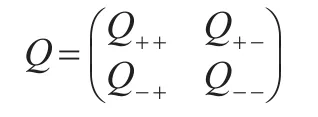

相應的轉移率矩陣記為Q(n),根據,將轉移率矩陣Q(n)改寫成如下分塊矩陣形式:
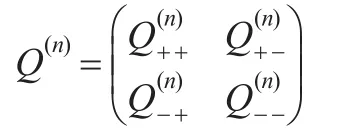
類似地,定義:
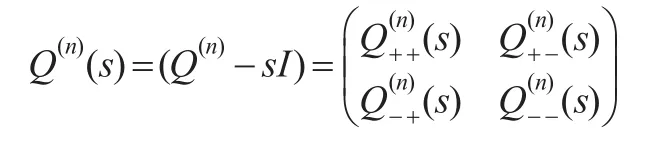
1.3 主要結果
基于MFQ序列{(V(n),J(n))},對n=1,2,3,…,定義首達時序列:
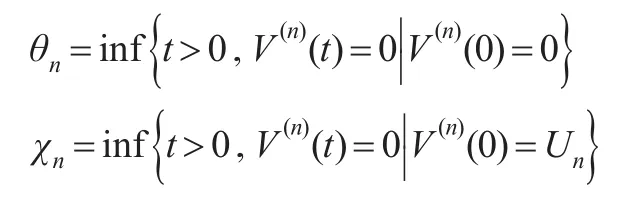
其中,θn表示{(V(n),J(n))}從初始水平為0首次回到初始水平0的時間。χn表示{(V(n),J(n))}從初始水平為Un首次達到水平0的時間。
類似地,定義θn與χn的LST變換矩陣,其中:

類似地,定義τn為MFQ{(V(n),J(n))}對應初值為Un的風險過程(1)的破產時刻,設τn的LST變換矩陣為
下面給出本文的主要定理及證明。
定理1:設給定初始盈余u及初始環境狀態i∈EJ,則MArP風險過程(1)的破產時間的LST變換u,s)滿足:

其中,符號A1·表示取矩陣A1·的第一行元素。有:
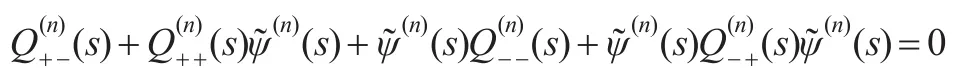
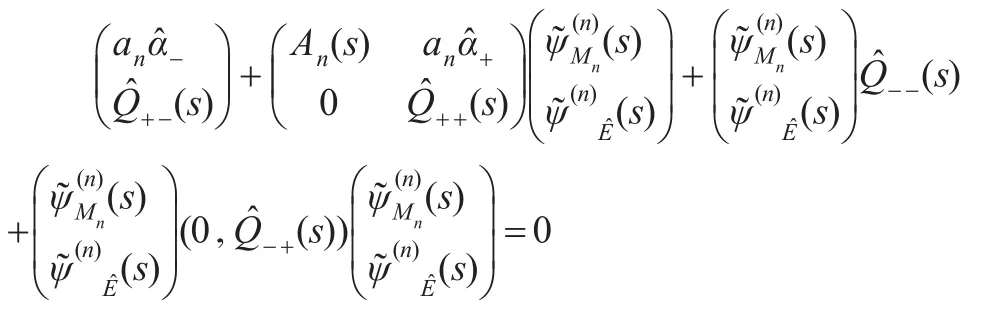
注意到初始環境狀態給定為i∈EJ,于是=ei,=0,其中,ei表示第i個元素為1,其他元素為0的維數適當的行向量。從而取上式第一行,得:

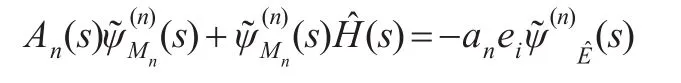
由文獻[10],解得上式:
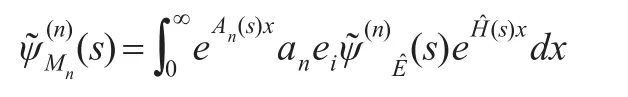
注意到An(s)=An-sI,于是有:
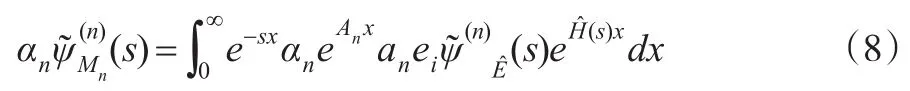
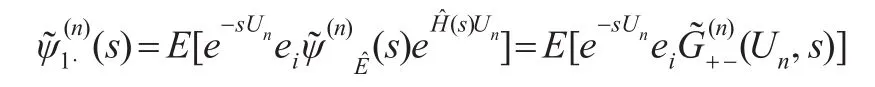
對應的仿文獻[7]推導,如圖3所示,在{(V(n),J(n))}中,有如下關系:
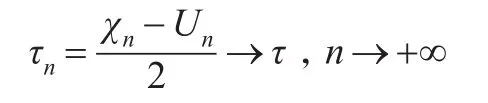
證明:由引理1,MFQ序列

圖3 Un,τn與χn的數量關系
于是:
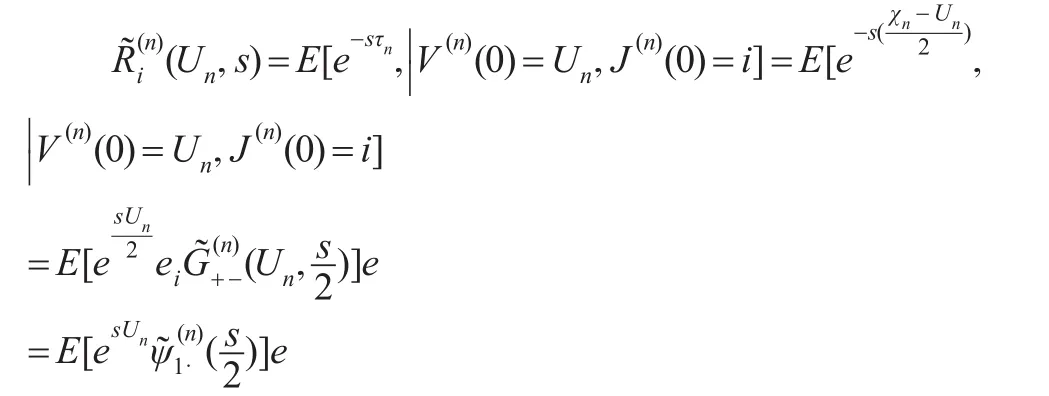
注意到,Un服從分布,故,當n→+∞時,隨機變量Un收斂為常數u(注:本文的收斂均指以概率1收斂)[11],于是,令上式左右兩邊同時令n→+∞,得到:

定理顯然。
②定理1給出了破產時間的LST變換的一個逼近算法,由文獻[11,13]可知,即使當階數n很小時,這一算法也具有優良的精度,文獻[9]中給出了破產時間LST的不同證明方法。顯然本文的證明方法更為簡潔明了。
顯然,令s=0,有如下推論成立:
推論1:設給定初始盈余u及初始環境狀態i∈EJ,則MArP風險過程(1)的最終破產概率為:

同時,根據PH分布的性質,可以推得如下結論:
推論2:設給定初始盈余u及初始環境狀態,則MArP風險過程(1)的破產赤字服從PH分布:
2 數值實例
為了說明本文的理論結果,下面給出一數值實例:考慮具有兩個風險狀態的MArP風險過程,設EJ={1,2},其中1表示高風險狀態,2表示低風險狀態,背景過程對應于不發生索賠和發生索賠的轉移率矩陣分別設為:當背景過程轉移至狀態1時,索賠服從分布PH(α,A),其中,α=(1,0),A=,背景過程轉移至狀態2時,索賠服從分布PH(β,B),其中設過程的初始盈余為u=1,于是,由定理1可以得到兩狀態下風險過程(1)對應的破產時間的LST變換函數,對LST變換函數取逆變換[12],于是得到兩風險狀態下破產時間的概率密度函數值如表2所示,從表中數據可見,本文提出的這種逼近新算法,借助了Erlang逼近速度快這一優點,不需計算任何中間量即可求得所需的性能指標。
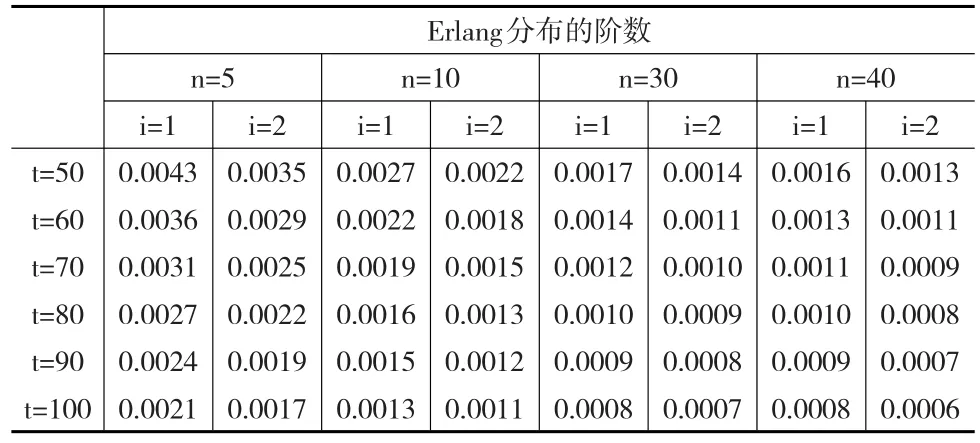
表2 兩風險狀態下破產時間的概率密度函數值
同時,根據本文推論1的結論,可以計算出在不同Erlang分布階數下風險狀態1和2的終破產概率,如圖4所示,從圖中可見,Erlang逼近的精度是可以滿足一般風險度量需求的[11]。
3 結論
本文分析了在隨機環境下的風險過程,即一類由Markov隨機環境過程同時影響風險過程的索賠大小及頻率,在索賠服從PH分布情形下,將這一風險過程轉化為MFQ模型,在轉換過程中,本文改進了Asmussen等轉換方法,即將風險過程轉化為一個初始水平為0的MFQ序列,這一轉換關系將對風險過程性能指標的討論限定在一個忙期內,從而使得問題求解的計算簡潔直觀,應用MFQ理論探討了這一風險過程的破產時間分布的LST變換的表示式,給出了最終破產概率以及破產赤字分布。本文的結論具有實際可操作性,這些結論對于保險公司分析外界隨機環境因素對保險業務的經營及管理的影響提供了理論基礎,對保險人規避風險,穩健經營具有重要的指導意義。
[1]Latouche G,Ramaswami V.Introduction to Matrix Analytic Methods in Stochastic Modeling[J].Technometrics,2012,43(3).
[2]Asmussen,Koole G.Marked Point Processes as Limits of Markovian Arrival Streams[J].Journal of Applied Probability,1993,l30(2).
[3]Ahn S,Ramaswami V.Efficient Algorithms for Transient Analysis of Stochastic Fluid Flow Models[J].Appl.Probab.,2005,42(2).
[4]Asmussen S.Stationary Distributions via First Passage Times[J].In Advances in Queueing:Theory,Methods,and Open Problems,1995.
[5]張超權,劉曉輝.求解MArP風險過程破產時間的新方法[J].統計與決策,2015,(21).
[6]Badescu A L,Breuer L,et al.Risk Processes Analyzed as Fluid Queues[J].Scand.Actuar,2005,(15).
[7]Badescu A L,David L.Applications of Fluid Flow Matrix Analytic Methods in Ruin Theory-A Review[J].Rev.R.Acad.Cerie A.Mat.2009,103(2).
[8]Ramaswami V.Passage Times in Fluid Models With Application to Risk Processes[J].Methodol.Comput.Appl.Probab.,2006,8(4).
[9]Tang S,Tan L.Erlangian Approximation to Finite Time Probability of Blocking Time of Multi-class OBS Nodes[J].Photonic Network Communications,2015,30(2).
[10]Bhatia R,Rosenthal P.How and Why to Solve the Operator Equation AX-XB=Y[J].Bull Lond Math Soc,1997,(29).
[11]Asmussen S,Avram F,Usabel M.Erlangian Approximations for Finite Time Ruin Probabilities[J].N Bulletin,2002,(32).
[12]Jagerman D L.An Inversion Technique for the Laplace Transform[J].Bell System Technical Journal,1982,61(8).
[13]Ramaswami V,Woolford D,Stanford D.The Erlangization Method for Markovian Fluid Flows[J].Annals of Operations Research,2008,(160).

