復合Linex損失下不同先驗分布中參數的Bayes估計
王敏
(貴州師范大學數學科學學院,貴陽550001)
0 引言
Linex損失是由Varian(1975)[1]提出的對稱損失函數,文獻[2]研究了在復合Linex對稱損失下正態均值以及指數分布參數的Bayes估計問題。艾拉姆咖分布是武器裝備維修理論中的常用分布,俄羅斯在研究武器裝備的維修時間時引進了艾拉姆咖分布。文獻[3]研究了在定數截尾場合下不同先驗對艾拉姆咖分布參數估計的影響,但是該文是在平方損失下做出的估計,在平方損失中不再引入新的參數,而在復合Linex損失函數中,還需要對尺度參數α做出估計。
本文在復合Linex對稱損失下,分別以伽瑪分布、共軛先驗以及無信息先驗為艾拉姆咖參數的先驗分布、得到了艾拉姆咖分布參數的唯一貝葉斯估計。通過對瑪分布分布中的超參數做了靈敏性分析及對共軛先驗艾拉姆咖分布中的參數給出了估計方法。并給出了艾拉姆咖分布參數的估計值,通過對比確定了一個較優的先驗分布。
1 艾拉姆咖分布參數的估計
單參數艾拉姆咖分布的概率密度函數與分布函數分別為:

F(x)=1-(1+λx)e-λx,其中x>0,且λ>0是參數。
由式(1)易知來自艾拉姆咖總體的樣本X1,X2,…,Xn的聯合概率密度為:
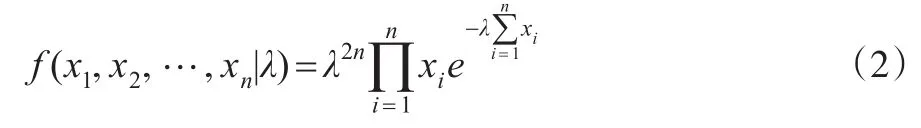
復合Linex對稱損失函數[2]形式為:

其中δ為λ的估計,a≠0是該損失函數的尺度參數。
引理1[2]:對于形狀參數已知的伽瑪分布,在給定尺度參數λ的先驗分布π(λ)和對稱損失函數(3)下,若存在估計δ,其貝葉斯風險r(δ)<∞,則λ有唯一的貝葉斯估計:

1.1 先驗分布為伽瑪分布的參數估計
定理1:設x1,x2,…,xn是來自艾拉姆咖分布的一組樣本觀察值,參數λ的先驗分布π1(λ)服從伽瑪分布Γ(θ,β),則λ具有唯一的貝葉斯估計:
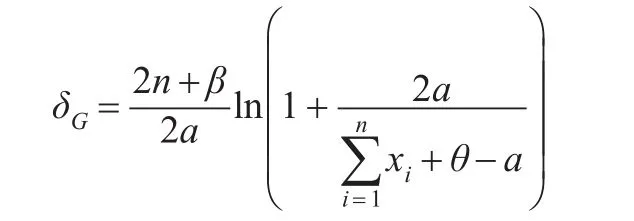
證明:因為參數λ的先驗分布π1(λ)服從Γ(θ,β),則λ的密度函數為:
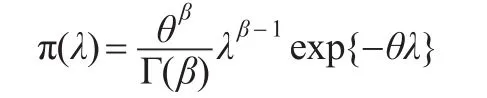
而樣本似然函數為:
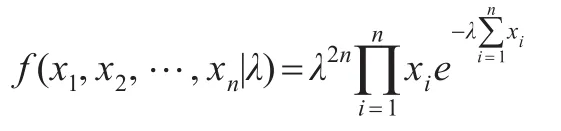
于是λ的后驗密度為:
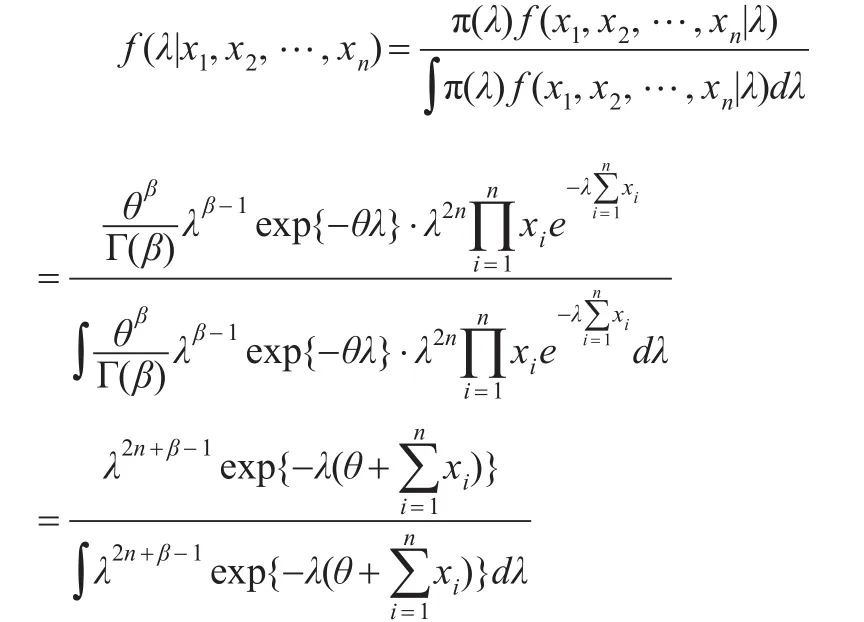
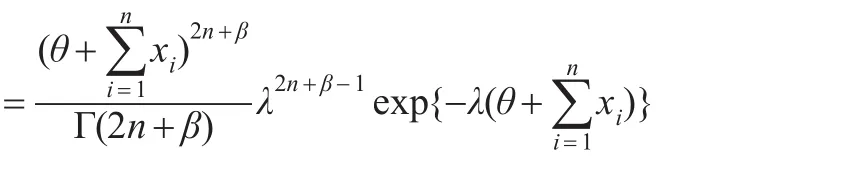

證畢。
1.2 共軛先驗下的參數估計
定理2:設x1,x2,…,xn是來自艾拉姆咖分布的一組樣本觀察值,參數λ的先驗分布π2(λ)也服從艾拉姆咖分布,則λ具有唯一的貝葉斯估計:
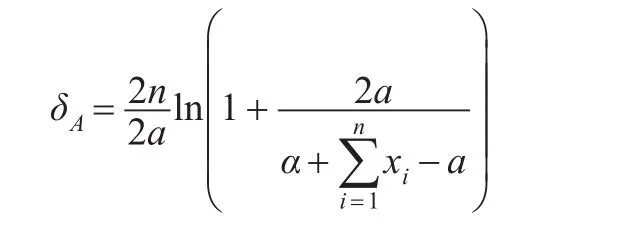
證明:因為參數λ的先驗分布π2(λ)服從共軛先驗,則λ的密度函數為:
π2(λ)=λ2αexp{-αλ},其中α為超參數
于是λ的后驗密度為:
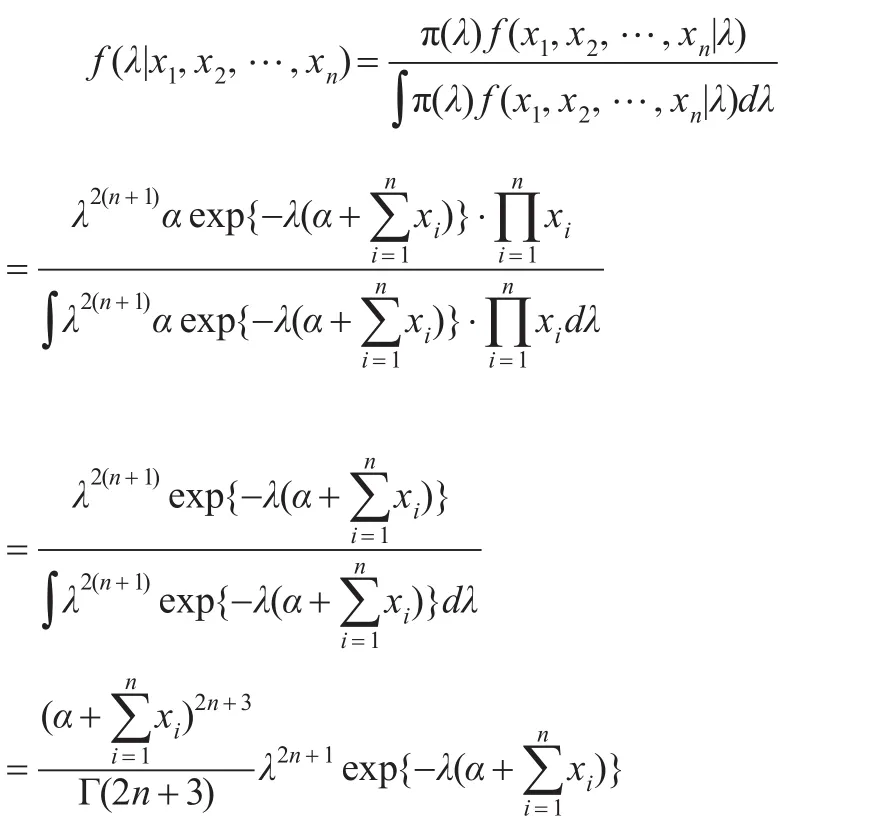
在復合Linex損失下,λ的Bayes估計為:
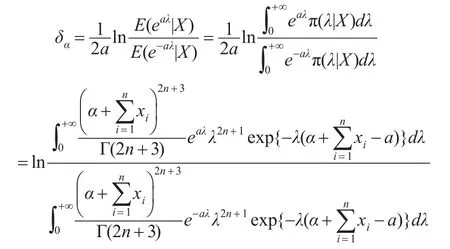
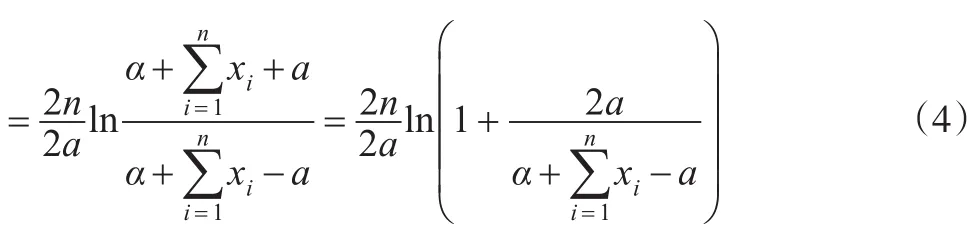
證畢。
1.3 無信息先驗下的參數估計
定理3:設x1,x2,…,xn是來自艾拉姆咖分布的一組樣本觀察值,參數λ的先驗分布π3(λ)服從無信息先驗,則λ具有唯一的貝葉斯估計:
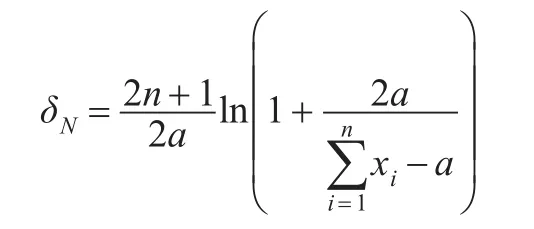
證明:參數λ的先驗分布π3(λ)為無信息先驗,即π3(λ)=1,于是λ的后驗密度為:
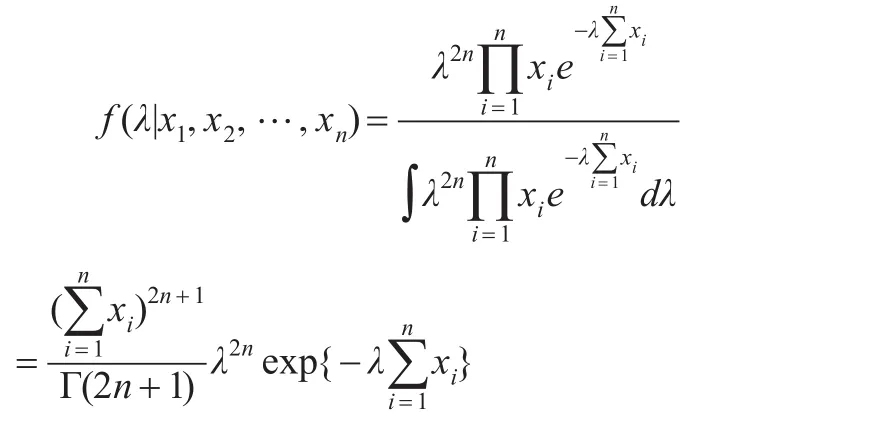
在復合Linex損失下有:
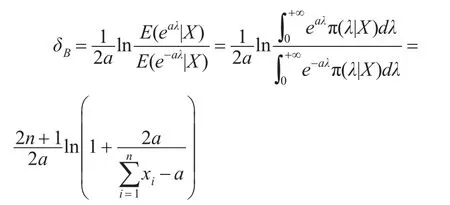
證畢。
2 先驗分布中參數的估計
對于復合Linex損失中尺度參數a的估計,可以參見文獻[4]中的討論,a取正負值對參數λ的后驗估計影響不大,因此本文取a=0.1。
2.1 伽瑪分布中兩個參數的估計
對于先驗分布伽瑪中的參數β與θ,取參數λ=1,樣本容量為20的艾拉姆咖樣本0.1586,0.4090,0.7420,1.0671,1.1866,1.3045,1.6034,1.6388,1.9408,2.0155,2.3368,2.3827,2.6109,2.7747,2.7836,2.7894,2.8058,2.8369,3.1529,3.2694.本文利用R軟件,隨機分別從一到十中重復取值1000次,得到β與θ的取值如下頁圖1所示,依次代入得到參數λ的均值為1.012044,均方差為0.08991331,由此看出參數β與θ并不靈敏,其取值對參數λ的影響不大,因此本文在后文的隨機模擬中直接取β=1與θ=1。
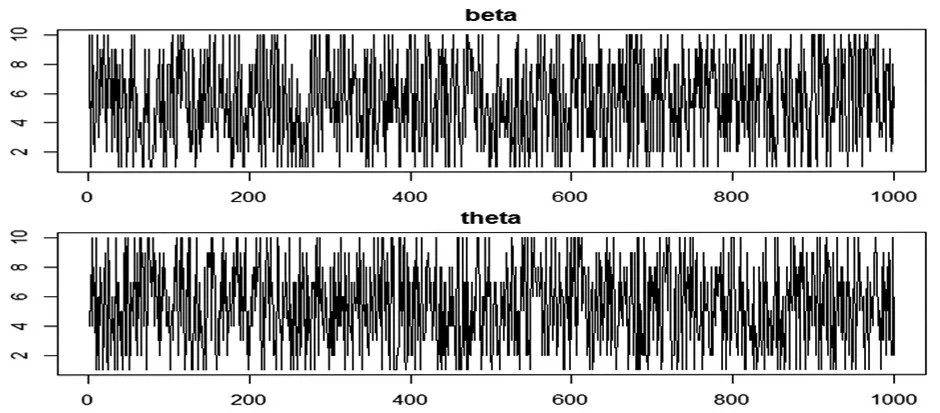
圖1
2.2 共軛艾拉姆咖分布中參數的估計
本文用極大似然法估計共軛先驗中的超參數α。
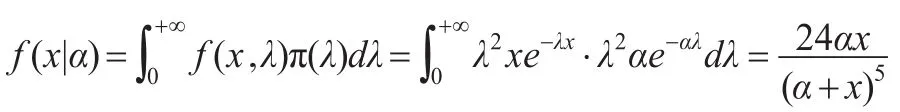
用f(x|α)代替式(1),則式(2)在此時為:
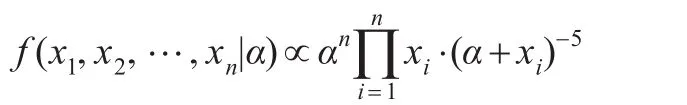
取自然對數并求導得到關于α的方程:

下文隨機模擬的估計中將通過R軟件解式(5),得到α的估計值再代入式(4)得到λ的E-Bayes估計δα。
3 隨機模擬
本文利用R軟件,通過Monte-Carlo法模擬產生兩組服從艾拉姆咖分布的隨機樣本。方法為隨機抽服從均勻分布的隨機變量值u,這里u~U(0,1),再由u=F(x)=1-(1+λx)e-λx,計算出x的取值,從而得到表1。
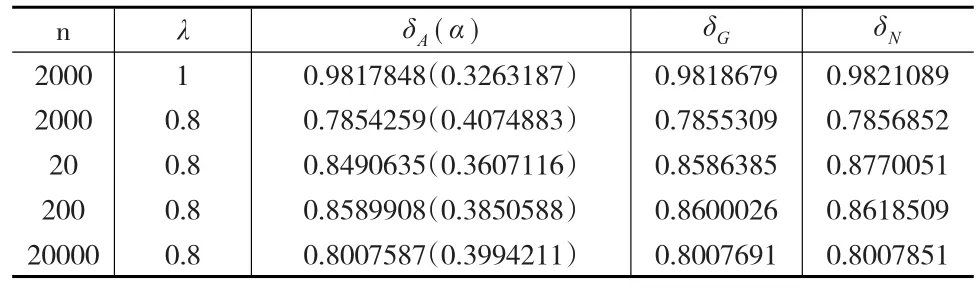
表1 參數的Bayes估計
從表1中看出,對于λ的不同取值,各不同先驗下估計都是一樣精確的。對于不同的樣本容量而言,樣本容量越大估計越精確,在樣本容量較小時,估計有一定的偏差。相比較而言,先驗分布為共軛先驗,即也為艾拉姆咖分布時,得到參數λ的Bayes估計最接近真值。
4 結束語
本文主要討論的是先驗分布對參數估計的影響,具體分析了在復合Linex對稱損失下,對拉姆咖分布參數的先驗分布為伽瑪分布、共軛先驗及無信息先驗進行了對比,并用R語言進行了模擬分析,得出各種先驗分布下分布參數的Bayes估計值,結果顯示,當先驗為共軛先驗時,估計值最接近艾拉姆咖分布參數的真值。
[1]Varian.A Bayes Approach to Real Estate Assessment[A].Fienberg S E,ZELLENER A.Studies in Bayesian Economics and Statistics in Honour of Lenoard J.Savage[C].Amesterdam:North Holland,1975.
[2]張睿.復合Linex損失下的參數估計[D].大連:大連理工大學碩士論文,2007.
[3]龍兵.不同先驗分布下艾拉姆咖分布參數的Bayes估計[J].數學的實踐與認識,2015,(4).
[4]龍兵.不同損失函數下艾拉姆咖分布參數的Bayes估計——全樣本情形[J].重慶師范大學學報:自然科學版,2013,(5).

