磁液變形鏡的鏡面動力學建模和實驗驗證?

張柱 吳智政? 江新祥 王園園 朱進利 李峰

1)(上海大學精密機械工程系,上海 200072)

2)(上海理工大學電氣工程系,上海 200093)

1 引 言

磁性液體(magnetic fluid),又稱磁性流體,是磁性納米微粒分散在基載液中形成的具有磁性又具有流動性的穩定膠體[1].當磁性液體處于磁場中時,懸浮的磁性納米微粒受到磁場作用力而影響基載液的流動性,利用變化的磁場與其相互作用能控制流體的運動[2,3].1965年,美國國家航空航天局(NASA)的Papell[4]首次將磁性液體用于宇航服可動部位的密封和火箭液體燃料在失重情況下的輸送.經過50多年的發展,磁性液體已經在密封[5]、潤滑[6]、阻尼減震[7]、生物醫療[8]、光學[9]等諸多領域得到廣泛應用.

利用磁性液體既具有液體的流動性,又具有可以被外磁場磁化而擁有磁性的特點,通過改變磁性液體周圍的磁場來精確控制磁性液體表面的變形.Nguyen等[10]提出了一種利用永磁鐵和平面線圈產生的磁場來控制微磁性液滴尺寸大小的方法.Liu等[11]設計了一種基于流體聚焦結構的微流控芯片,利用U型電磁線圈產生的磁場來控制磁性液滴的尺寸大小和運動速度.Brousseau等[12,13]基于磁性液體設計了一種液態可變形反射鏡來糾正光學系統中的波前像差和控制激光束的波前,反射鏡的鏡面由液體下方的電磁線圈陣列產生的磁場發生變形.Borra等[14]設計了一種通電銅導線網格驅動器驅動的磁液變形鏡,用來校正液體望遠鏡系統中因大觀測角度和運行過程中速度波動引起的離軸像差,但是鏡面面形對輸入電流的響應是非線性的.Iqbal和Amara[15]通過亥姆霍茲線圈在磁性液體區域產生大均勻垂直磁場的方法,使磁液變形鏡的鏡面響應線性化并且增大了鏡面變形行程.因為磁液液體鏡面低反射率的缺點使得磁液變形鏡不能有效地應用于自適應光學系統中,文獻[16–18]通過在磁性液體表面覆蓋一層銀液狀薄膜或者彈性反射薄膜的方法有效地提高了變形鏡鏡面的反射率.Wu等[19,20]通過Maxwell線圈產生大均勻磁場和微小電磁驅動線圈產生的擾動磁場來精確控制磁液變形鏡的鏡面變形,證明了其鏡面變形行程能達到100μm并能精確控制激光束的波前.相比于傳統的固態變形鏡[21?23]和液晶空間光調制器[24?26],磁液變形鏡具有鏡面連續平滑、變形行程大、制造成本低、驅動器易擴展等優點.

由于磁液中的磁性納米顆粒相互之間的磁吸引力、van der Waals力和表面活性劑產生的排斥力,磁液受流體磁壓力、熱力學壓力的影響,使得在重力場、電場和磁場多物理場耦合情況下很難對磁液變形鏡鏡面變形進行準確的建模.Ghaffari等[27]運用Maxwell方程和動量方程對磁性液滴建模,采用水平集(level set)和流體體積(volume of fluid)相耦合的方法對受均勻磁場作用的磁性液滴的聚集形狀進行了數值模擬和實驗驗證.Shi等[28]運用Maxwell方程和兩相流Navier-Stokes方程對處于均勻磁場中運動的磁性液滴進行了建模,采用VOSET界面追蹤數值方法來仿真磁性液滴的表面形狀;文獻[3]分別建立了在水平和垂直均勻磁場作用下的磁性液體液面變形模型,但假設變形磁液面只發生整體向上的變形,變形之后的液面仍然是水平的,無法產生特定的面形.Brousseau等[12,13]對磁液變形鏡在擾動磁場作用下的鏡面響應進行了推導計算,但是為了簡化推導過程,只計算了鏡面在最大變形處的靜態變形量,因而無法從該變形模型中獲得各個驅動器之間的影響函數及系統的動態性能.Wu等[19]針對受均勻磁場和擾動磁場相疊的磁場作用的磁性液體,在柱坐標系下運用Laplace方程和Maxwell方程對液面的變形建模,引入第一類和第二類Bessel函數,采用分離變量的方法推導出磁液變形鏡的動力學方程.但是這一類建模都是針對圓形的磁液變形鏡,而且也沒有考慮磁液容器的厚度,導致模型的精度降低.

在一些領域,例如激光微加工系統[29]、微激光推進系統[30]和高能激光系統[31]等中,激光束的幾何輪廓是方形的,圓形幾何形狀的變形鏡因為鏡面利用率低以及驅動器的圓形或者三角形排布方式而不能有效地控制方形激光束的波前.為了更有效地控制方形激光束的波前和糾正波前像差,本文以基于方形驅動器陣列的磁液變形鏡為例,考慮磁性液體受重力場、電場和磁場多物理場耦合的作用,在笛卡爾坐標中運用Laplace方程和Maxwell方程,并且在考慮磁液容器厚度的情況下建立了磁液變形鏡的模型,通過引入歐拉函數和采用分離變量的方法推導出磁液變形鏡的鏡面動力學方程.然后基于該理論模型,設計了磁液變形鏡的結構和參數以滿足鏡面變形要求.最后通過MATLAB,COMSOL Multiphysics和Tracepro軟件聯合仿真及在自適應光學系統中的實驗測試,驗證了所建模型的準確性和磁液變形鏡的響應性能.

2 磁液變形鏡建模

如圖1所示,磁液變形鏡在笛卡爾坐標系中可以表示為一個立方體形的磁性液體.鏡面的面形定義為液面相對于初始平整狀態時的變形.設鏡面在任一點(x,y)處的變形為ζ(x,y,t),是通過磁性液體下方驅動器產生的擾動磁場而發生的變形.設磁液的厚度為d,磁液面到容器底部的距離為h,容器的長寬分別為Lx和Ly.表1列出了建立磁液變形鏡模型所涉及的參量.

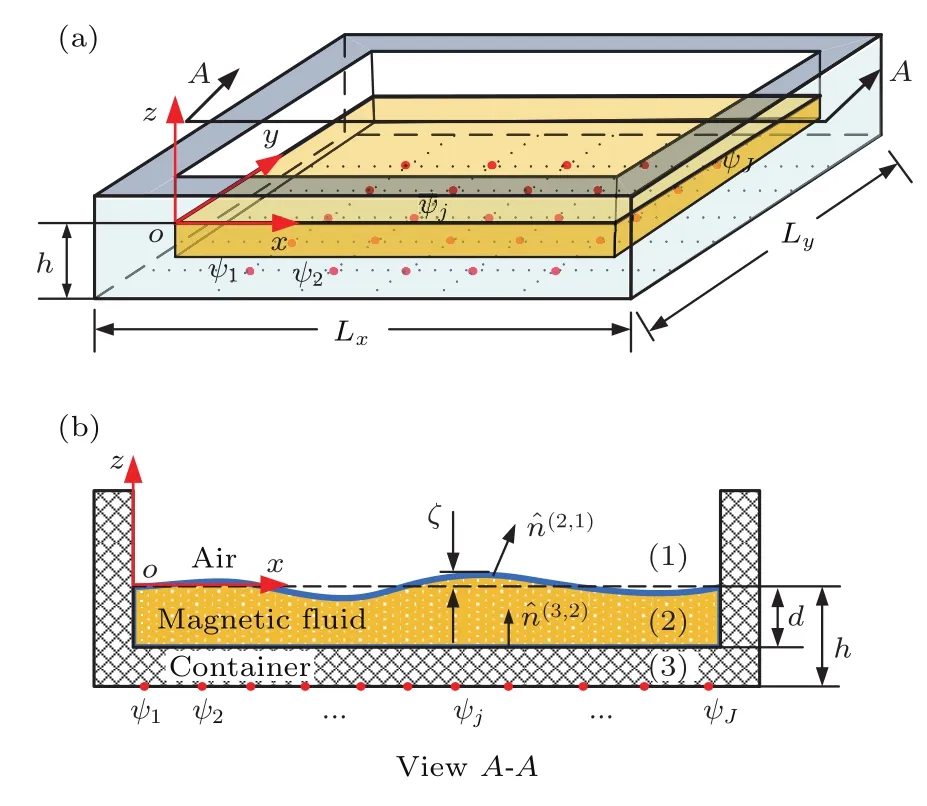
圖1 方形磁液變形鏡示意圖(a)三維視圖;(b)A-A剖面圖Fig.1.Geometric representation of the square magnetic fluid deformable mirror:(a)Three-dimensional view;(b)A-A view.

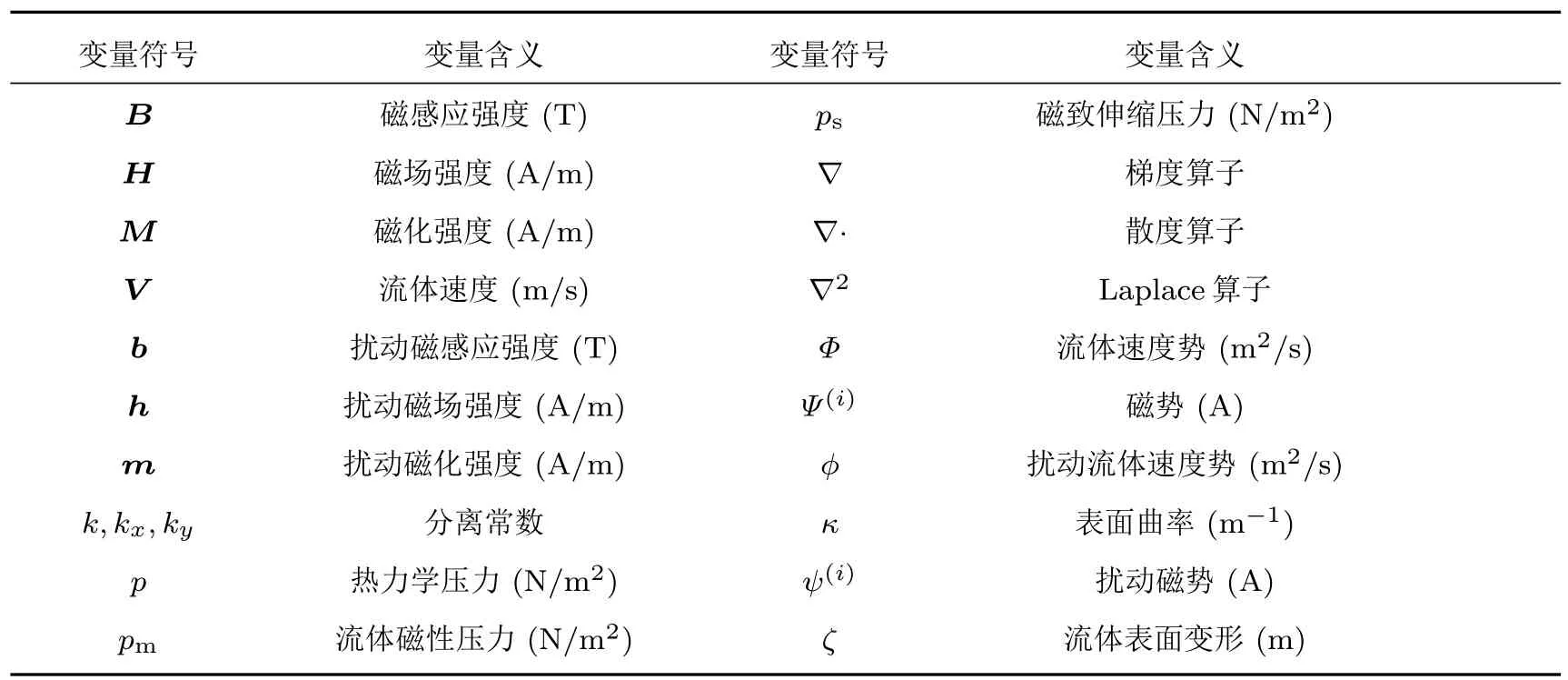
表1 符號說明Table 1.List of symbols.

2.1 磁液的控制方程

磁性液體自由表面的變形遵循流體動力學的基本原理,考慮磁場的影響并根據質量和動量守恒定理,磁液流體場的控制方程式為[3]

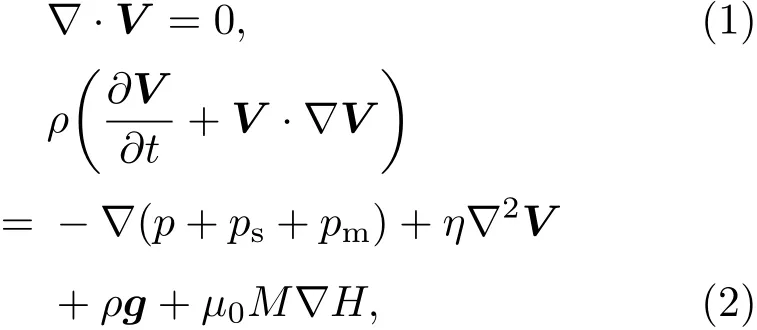
式中,V表示流體速度;p,ps和pm分別表示熱力學壓力、磁致伸縮壓力,磁性壓力;ρ和η分別表示流體的密度和黏度;μ0表示真空磁導率;M和H分別是磁化強度矢量M和磁場強度矢量H的大小.

假設磁性液體是不可壓縮、非旋流體,磁性液體上方的空氣是不可磁化而且磁導率是各向均勻的,且磁致伸縮壓力ps可忽略不計,那么結合方程(1),磁性液體的速度勢Φ和磁勢Ψ(i)滿足下列方程:

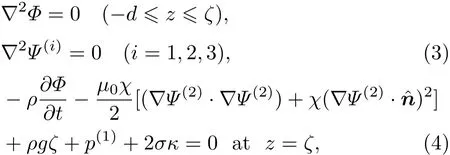
式中,是磁液面的單位法向量,為空氣熱力學壓力;2σκ是毛細壓力,表示為磁液表面張力系數σ和表面的平均曲率κ的函數,Vz是磁流體速度V的垂直分量,V用標量勢Φ表示為V=??Φ.磁場強度向量H(i)用標量勢表示為分別表示磁液面上方的空氣區域、磁性液體區域和容器底部區域.

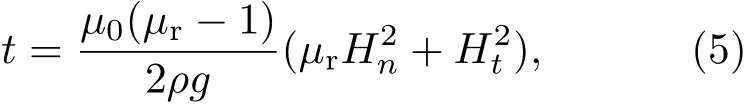
通過求解方程(3)和(4)可以得到ζ,?,ψ(i),i=1,2,3的解.但是方程(4)是關于磁勢Ψ(i)的非線性方程,線性求解方法不適用于求解這種形式的方程.為了簡化該方程的求解,Brousseau等[13]推導出了磁性液體面形在變形最大處的解:這里μr是磁性液體的相對磁導率,Hn和Ht是磁場強度的法向和切向分量.從結果中可以看出磁性液體的最大變形與輸入磁場是非線性二次型關系.這就意味著傳統的線性控制算法不適用于磁液變形鏡鏡面面形的控制.因為鏡面變形與輸入磁場的平方成正比,鏡面只能產生單向的變形,也就是磁性液體只能向上凸起變形,不能向下凹變形.

為了使磁性液體鏡面響應線性化,從而能運用現有成熟的線性控制算法控制鏡面面形,本文提出了將磁通量密度為B0大均勻垂直磁場施加于整個磁性液體區域的方法使磁液變形鏡的輸出線性化.由于在整個磁性液體區域施加的為均勻磁場,磁場的梯度為0,其鏡面的初始狀態將仍然保持完全水平,即ζ=0,從而方程(4)左邊的ρgζ項和項為0,磁液面的單位法向量,磁性液體的速度勢Φ0和磁勢Ψ0(i)滿足下列方程:

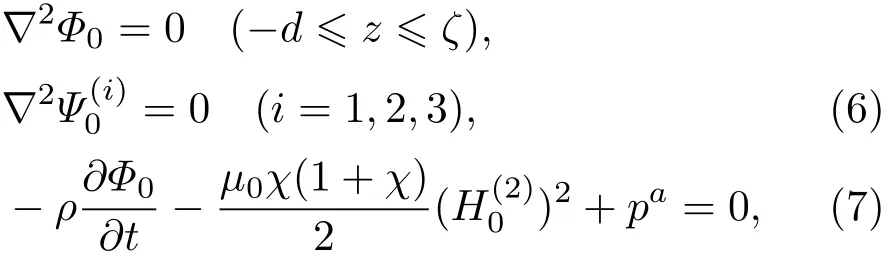
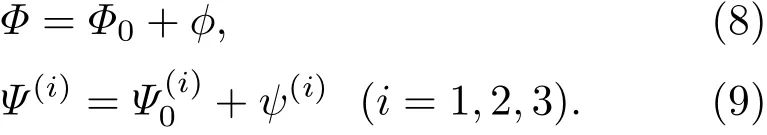
這里ψ(i)是擾動磁場強度h(i)(i=1,2,3)相對應的磁勢,它們之間的關系式為

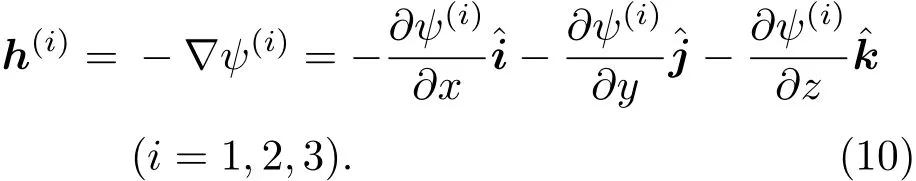
將方程(8),(9)和(10)代入到方程(4)中得到如下等式:

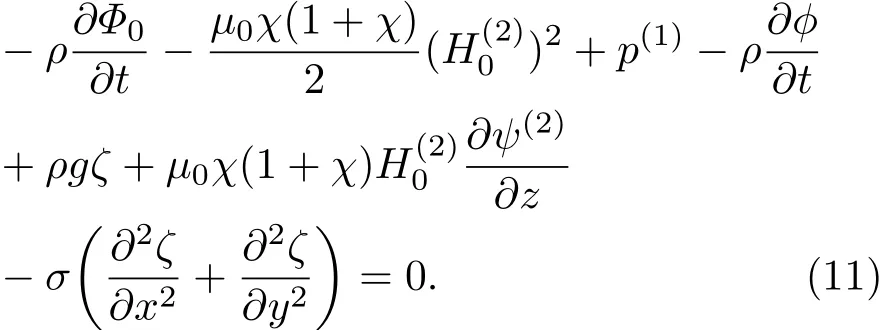
將方程(6),(8),(9)代入到方程(3),將方程(7)代入到方程(11),得到如下等式:

2.2 鏡面響應推導

以下采用分離變量的方法對ζ,?和ψ(i),(i=1,2,3)這五個未知量求解:

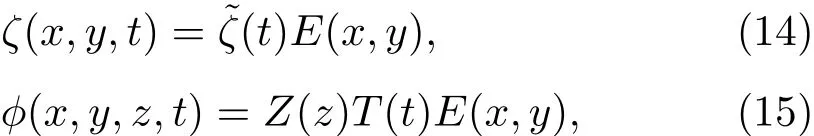
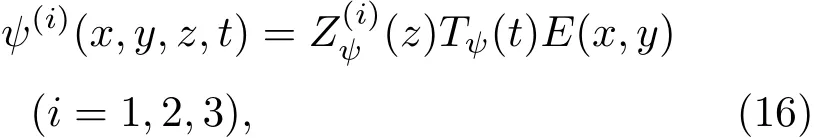
這里

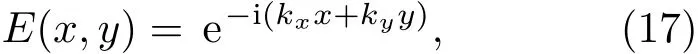
其中kx和ky為模數.方程(12)中的Laplace方程?2?=0將根據以下兩個邊界條件求解:

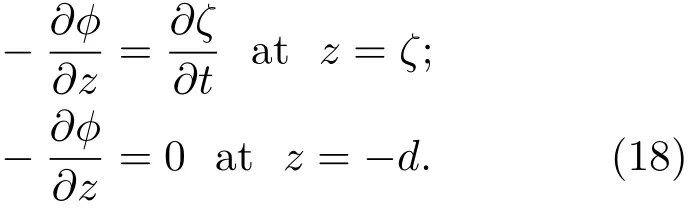
根據方程(12)和(15),得到如下的常微分方程:

該微分方程(19)的通解形式為

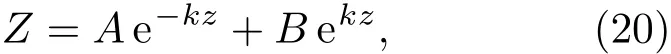
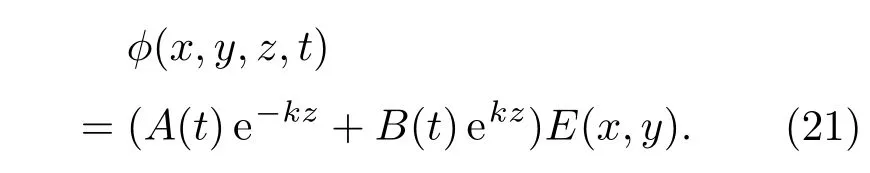
運用邊界條件(18),同時求解A(t)和B(t),從而得到

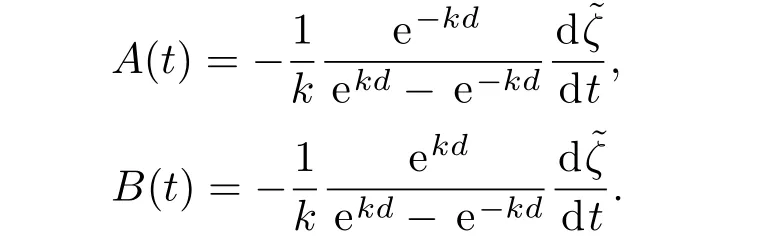
將A(t)和B(t)代入到方程(21)得到?的解為

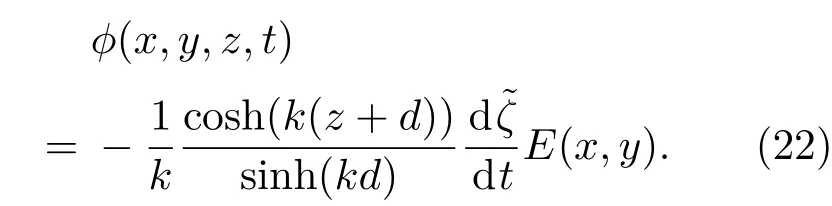
方程(12)中的磁場ψ(i),i=1,2,3將基于下面的邊界條件求解:

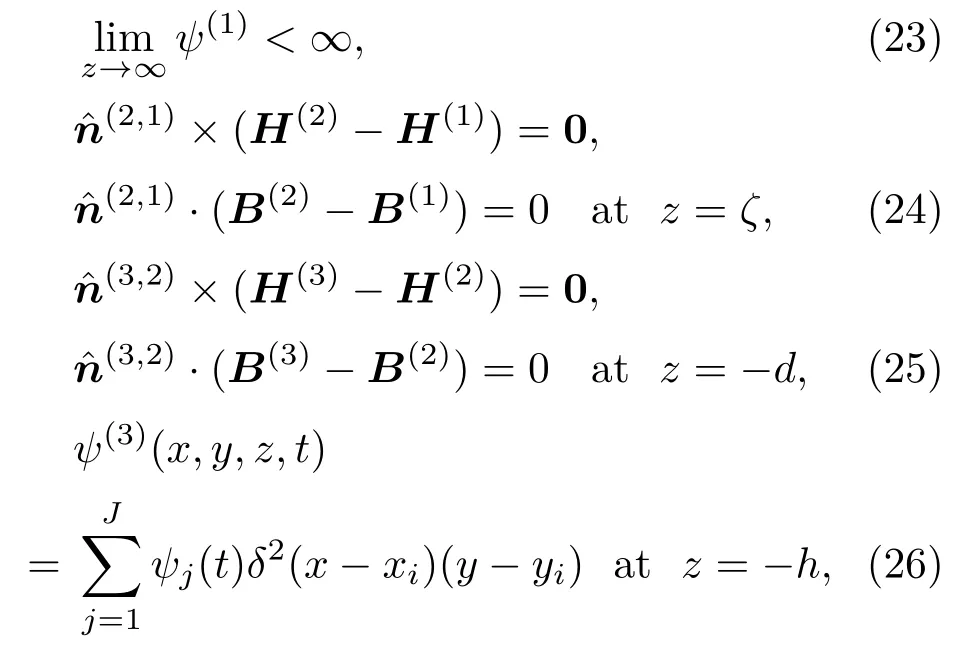
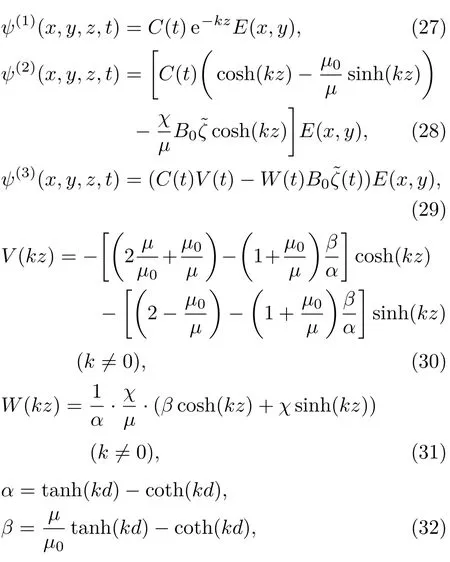
這里C(t)是積分常數,將使用方程(26)來確定其值;對于k=0的特殊情況,V(kz)=1,W(kz)=1.

考慮到垂直于容器壁的速度和磁場分量必須為零的條件,得到如下模態振型:

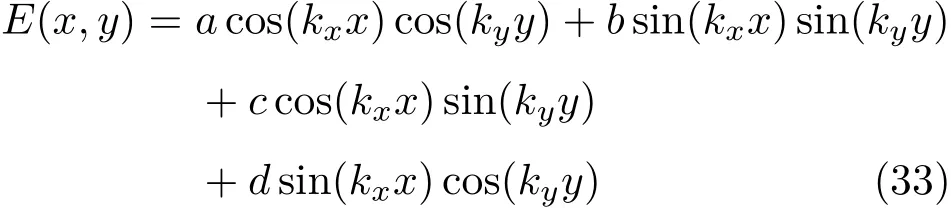
和特征方程

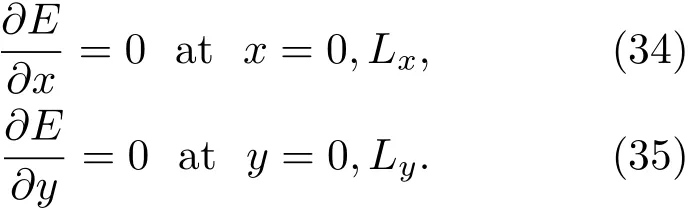
模態方程(33)需要滿足特征方程(34)和(35),E(x,y)必須為

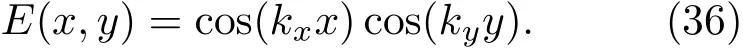
等式(34)–(36)可以由無窮多個離散值kx和ky來求解,即

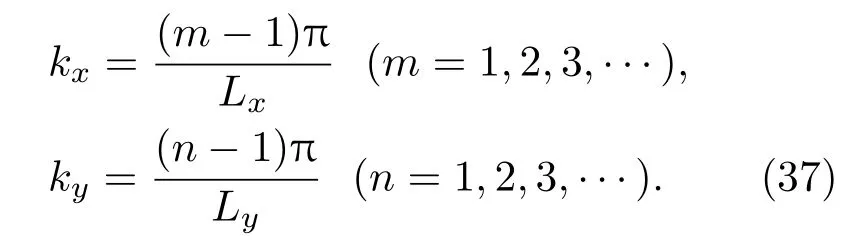
以輸入磁勢方程(26)作為邊界條件,根據模態振型的正交性確定每個模態相對應的參數C(t)為

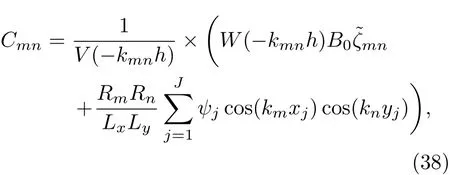
這里km,kn和kmn分別表示kx,ky和k對應于模數m,n的離散參數;變量Rm和Rn為

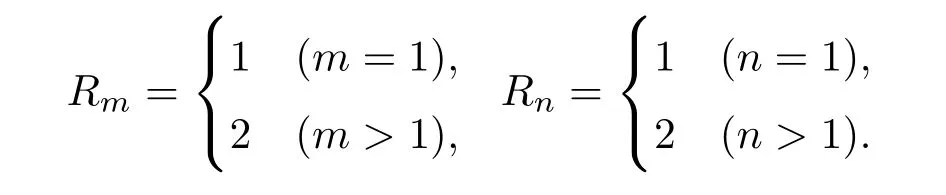
將上述對?,ψ(1),ψ(2)和ψ(3)求得的解方程(22),(27),(28)和(29)代入到方程(13)得到如下等式:

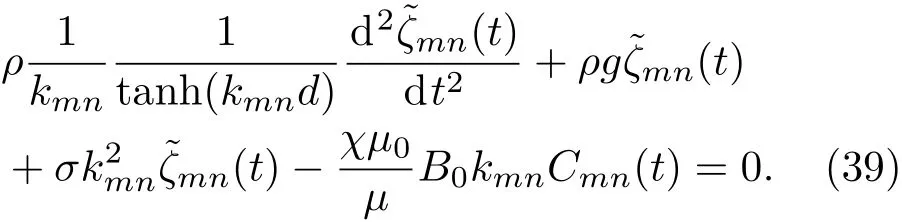
將方程(38)代入到方程(39)中以及考慮到文獻[32]中提到的磁液黏性對阻尼效應的影響,可以獲得磁液變形鏡鏡面動力學方程為

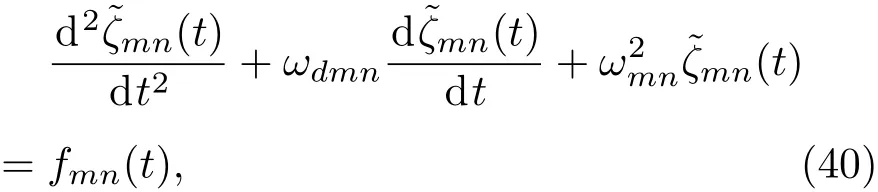
其中

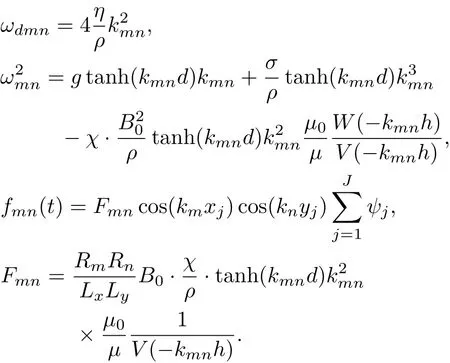
通過求解二階微分方程(40)可以得到磁液變形鏡鏡面廣義變形量,從而在任一位置(xk,yk)處鏡面的變形為

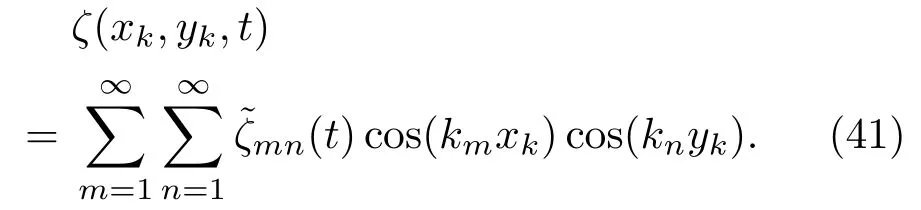
磁液變形鏡鏡面響應方程(41)可進一步表述為相應的狀態空間表達形式:

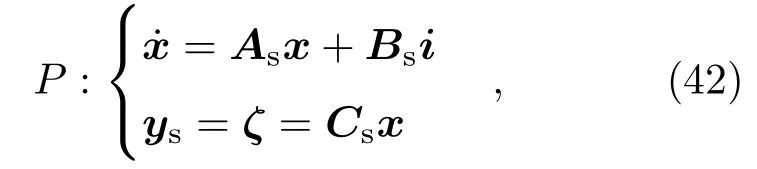
這里x是系統的狀態向量,i=[i1,i2,i3,···,iJ]T是微線圈陣列的輸入電流向量,ys=[ζ1,ζ2,ζ3,···,ζK]T是磁液變形鏡鏡面在各個采樣點處的變形量;As,Bs和Cs為相應的系統矩陣.

3 磁液變形鏡的設計和仿真

3.1 結構和參數設計

在本節中提出了磁液變形鏡的設計方法,并以產生拋物面面形為例來設計基于方形微線圈驅動器陣列的磁液變形鏡.為了使磁液變形鏡的變形線性化以及能產生大變形行程,采用Maxwell線圈產生大均勻垂直磁場.基于推導的理論模型,為了使磁液變形鏡產生100μm以上的變形行程,運用COMSOL Multiphysics仿真軟件確定大均勻磁場的磁通量密度B0和微線圈在磁液面處產生的最大擾動磁場bz分別為7 mT和0.4 mT.Maxwell線圈由三個分立線圈組成,結構參數如圖2所示,為了在Maxwell線圈內部產生一個較大的均勻磁場,上下兩個小線圈與中間大線圈的安匝比必須滿足49:64,上下兩個小線圈的半徑與中間大線圈的距離分別為.根據畢奧-薩伐爾定律,在Maxwell線圈中心處的磁場為

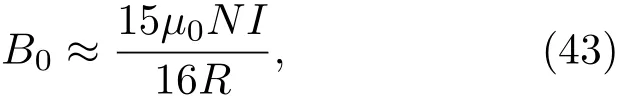
這里N是中間線圈的匝數,R為中間線圈的半徑,I為電流的大小.為了使Maxwell線圈能在其中心產生B0=7 mT的均勻磁場,中間線圈的半徑確定為R=100 mm.當輸入電流I=500 mA時,根據方程(43)中心線圈的匝數確定為N=1125,上下線圈的匝數都為883.Maxwell線圈的參數如表2所列.

根據狀態空間方程(42),磁液變形鏡的鏡面在輸入電流為i0時的靜態響應表示為

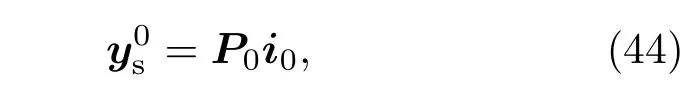
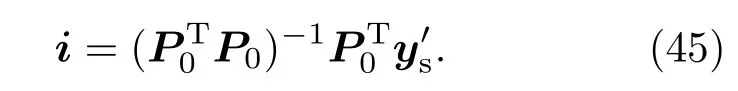
那么鏡面實際面形與期望面形的RMS誤差為

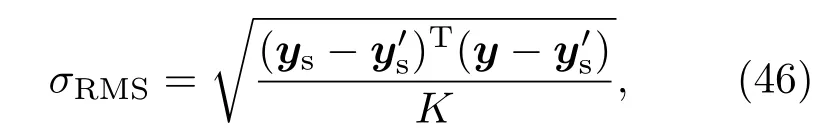
這里K表示鏡面變形的采樣點數.根據bz=4 mT的設計要求,確定微線圈的外徑和內徑分別為4 mm和2 mm,AWG36銅線匝數為800匝[34].基于方程(45)和(46),為了使RMS誤差值小于以及能讓磁液變形鏡的相鄰驅動器之間的耦合系數位于15%–35%之間[35],確定微線圈中心間距為4.2 mm,并采用如圖2所示的正方形排布.

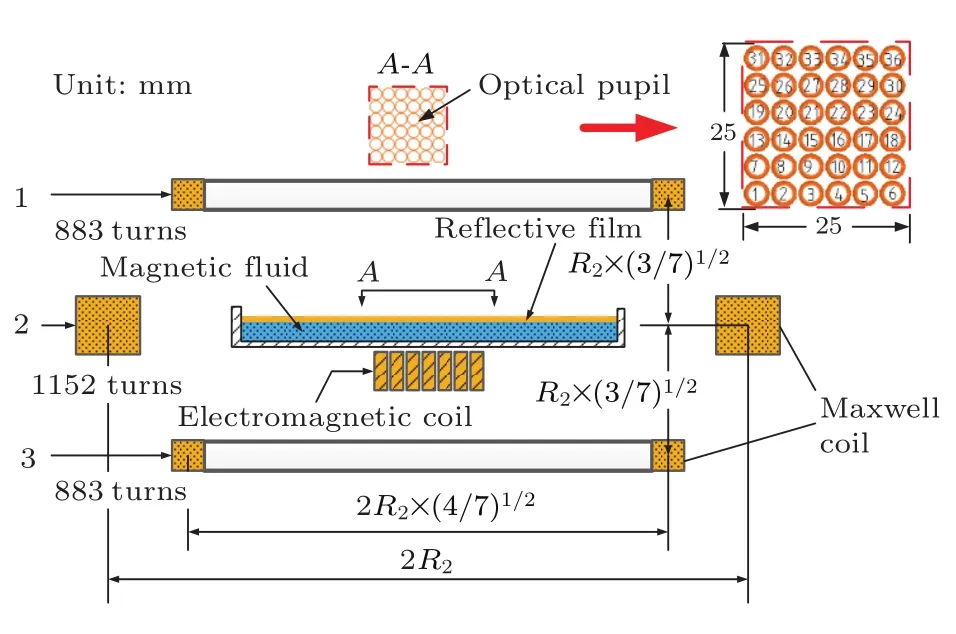
圖2 方形磁液變形鏡裝置的結構示意圖Fig.2.Schematic diagram of the square magnetic fluid deformable mirror.

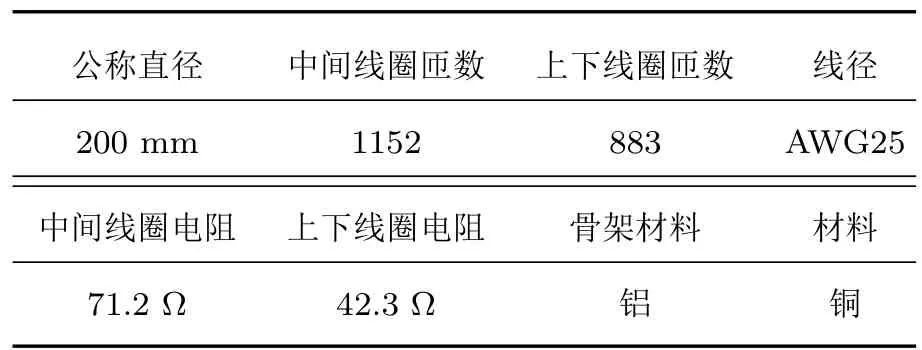
表2 Maxwell線圈參數Table 2.Parameters of the Maxwell coil.

3.2 仿真結果

基于上述推導的模型和所設計的結構參數,利用COMSOL Multiphysics和MATLAB軟件聯合仿真了方形磁液變形鏡的鏡面響應.仿真中磁液的基本參數和模型參數如表3所列.首先,對單一線圈施加電流后的鏡面響應進行了仿真分析.對中心線圈施加恒定電流后的鏡面面形仿真結果如圖3(a)和圖3(b)所示,從圖中可以看出,單一通電微線圈所產生的鏡面為高斯面形,而且其峰值位于通電線圈中心的正上方.圖3(c)所示為中心微線圈在通?60–60 mA電流下產生的鏡面形狀二維輪廓曲線,由圖可知線圈之間的交連值約為30%,當微線圈的輸入電流為60 mA時,磁液變形鏡實現了100μm以上的大行程響應.鏡面在微線圈陣列通入(45)式所示的電流后所產生的拋物面面形仿真結果如圖4所示.

表3 仿真參數Table 3.Simulation parameters.

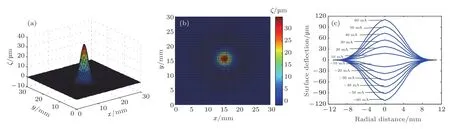
圖3 中心微線圈在通15 mA電流下產生的鏡面面形的仿真結果(a)三維視圖;(b)俯視圖;(c)鏡面面形x軸向輪廓圖Fig.3.The surface de flection of the central coil with current of 15 mA:(a)Three-dimensional view;(b)top view;(c)x pro file of surface de flection.

圖4 基于理論模型所產生的拋物面面形(a)三維視圖;(b)俯視圖Fig.4.The parabolic surface shape generated by the magnetic fluid deformable mirror:(a)Threedimensional view;(b)top view.

利用MATLAB,COMSOL Multiphysics和Tracepro軟件對方形磁液變形鏡的鏡面產生方形聚焦激光束進行了聯合仿真并分析該聚焦光束的質量.圖5為自適應光學系統仿真示意圖,利用第一級R1和R2第二級光束擴束組和對激光源所產生的圓形光束進行放大,放大后的光束通過孔徑為15 mm×15 mm方形光闌得到方形光束.拋物面對方形光束聚焦后并以7°–10°的反射角度將其反射到波前傳感器和電荷耦合器(CCD)相機上,CCD相機放置在聚焦光路z=20 mm處.為了使聚焦后的光束全部位于波前傳感器的傳感區域,反射光束需要第三級縮束組R3進行縮小.在圖6中可以看出聚焦光束的輪廓仍然是方形的,并且光束的強度分布很均勻.

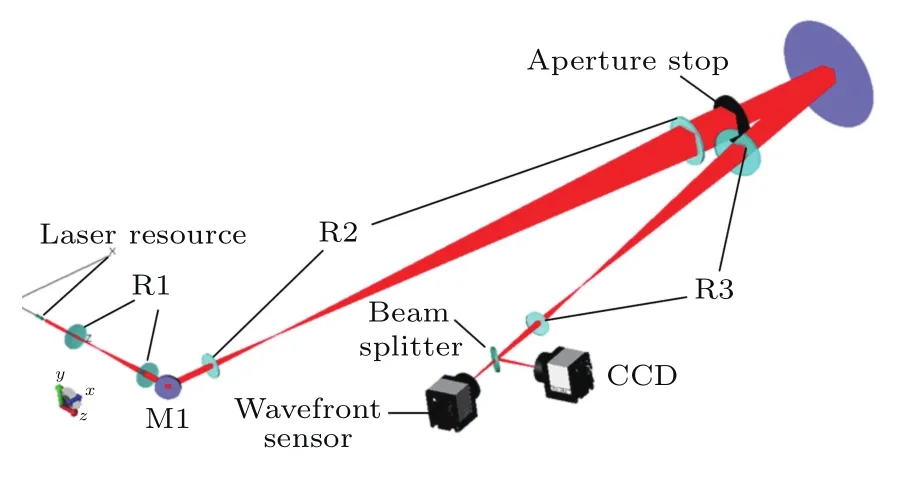
圖5 自適應光學系統仿真示意圖Fig.5.Layout of simulation adaptive optics system.

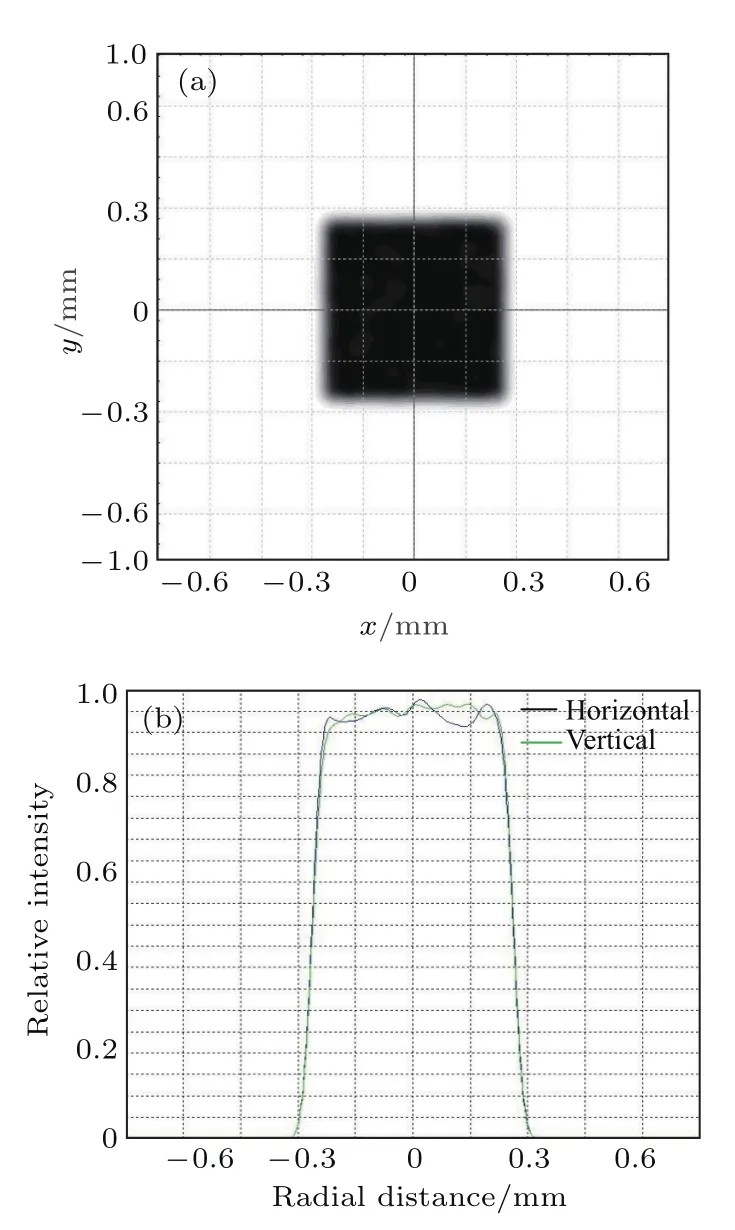
圖6(a)聚焦光束能量分布圖;(b)x和y軸向能量分布圖Fig.6.(a)The pro file of focused beam;(b)x and y pro file of focused beam.

4 實驗驗證

4.1 磁液變形鏡鏡面線性響應和動力學特性

根據上述所設計的結構參數,制作了磁液變形鏡原型樣機.如圖7所示,該磁液變形鏡主要由方形微線圈陣列、Maxwell線圈、磁性液體和容器支架組成.在本節中,首先通過實驗驗證磁液變形鏡鏡面大行程線性響應特性.如圖8所示,用激光多普勒干涉儀(Polytec,Germany)測量微線圈中心正上方處鏡面的變形量,微線圈從?60 mA到60 mA每隔10 mA依次加載電流,并記錄鏡面的變形量.在實驗過程中,Maxwell線圈的驅動電流為500 mA,在中心區域產生的磁通量密度為7 mT.

圖7 磁液變形鏡裝置(a)Maxwell線圈;(b)微線圈陣列;(c)磁性液體Fig.7.The magnetic fluid deformable mirror:(a)The Maxwell coil;(b)electromagnetic coils array;(c)the container with magnetic fluid.

圖8 磁液變形鏡鏡面線性響應實驗測試平臺Fig.8.Experimental setup for linear surface response of magnetic fluid deformable mirror.

如圖9所示,藍色“°”標記點和紅色“?”標記點分別表示磁液變形鏡的解析模型和實際鏡面在微線圈中心正上方所產生靜態面形的波峰或波谷值,藍色虛線和紅色點劃線分別表示解析模型鏡面和實際鏡面變形量的擬合曲線.可以明顯地看出,在微線圈中心正上方的鏡面響應輸出與輸入電流成線性關系,并能實現鏡面的雙向100μm以上的變形.

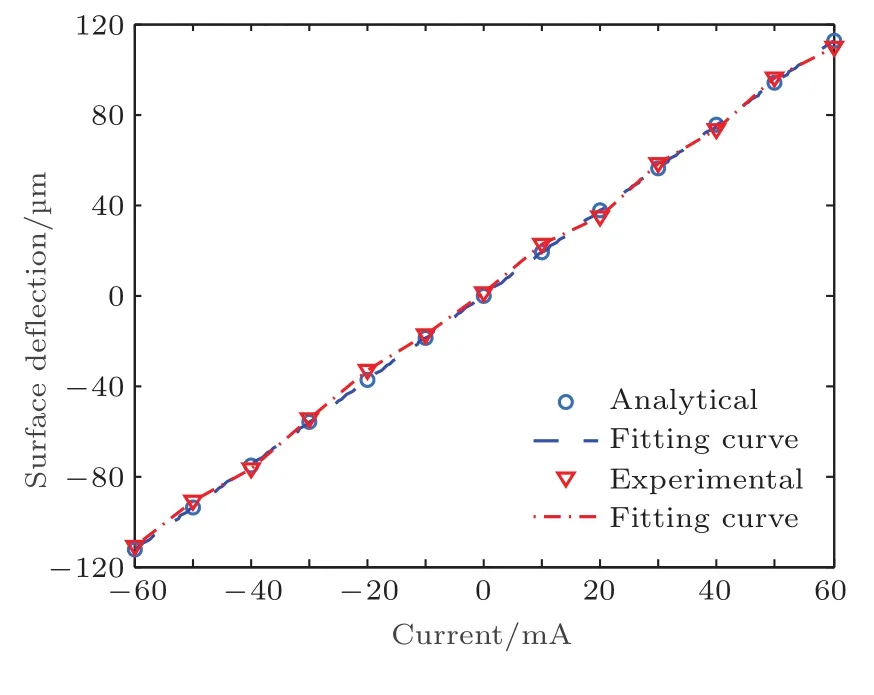
圖9 磁液變形鏡鏡面在微線圈中心正上方處的變形量Fig.9.The surface de flection at the top of the miniature electromagnetic coil center.

為了驗證磁液變形鏡在微線圈驅動下鏡面響應的影響函數和線性疊加特性,根據仿真系統搭建了基于波前傳感器的自適應光學系統,圖10所示為該系統實驗測試平臺.測試實驗系統由激光光源、磁液變形鏡、波前傳感器、CCD相機、計算機控制平臺和反射鏡、光束擴束透鏡組、光束縮束透鏡組、分束鏡、光闌等光學元器件組成.夏克-哈特曼型波前傳感器(WFS150-5C,THORLABS,USA)用來測量鏡面的面形.CCD相機(DCU223C,THORLABS,USA)用于對聚焦光束的成像和測量聚焦光束的幾何尺寸和強度分布.

圖11(a)所示為單一微線圈在通15 mA電流時磁液變形鏡鏡面面形,圖11(b)所示為基于波前傳感器記錄的數據得到的鏡面面形和軸向輪廓圖.可以看出,單一微線圈產生的鏡面面形近似為高斯形,并且相鄰驅動器之間的耦合系數約為30%.因為WFS150-5C波前傳感器的變形行程檢測范圍小于60μm,所以實驗中微線圈的輸入電流控制在?25–25 mA之間.

圖10 基于波前傳感器的磁液變形鏡鏡面控制實驗平臺Fig.10.Layout of the experimental system setup based on the wavefront sensor.

圖12所示是驗證磁液變形鏡鏡面響應在各個采樣點處的線性疊加結果.在圖12(a)中,以“°”標記的點代表中心的微線圈(#15)分別在輸入電流為25 mA和?15 mA時的鏡面響應,兩種鏡面響應曲線的疊加結果如紅色實線所示.綠色虛線代表#15線圈在輸入電流為10 mA時的鏡面響應.在圖12(b)中,以“×”標記的點分別代表#15線圈和其左邊最近的#16線圈分別在輸入電流為20 mA和?10 mA時的鏡面響應,綠色虛線則代表這兩種鏡面響應的算術和;當兩個線圈同時輸入上述電流時鏡面的響應如紅色實線所示.從圖12可以看出,代表實驗結果的紅色實線與代表線性算術和的綠色虛線基本重合.結合圖9和圖12可以看出,磁液變形鏡不僅在微線圈中心正上方的響應輸出與輸入電流成線性關系,在整個鏡面面形各點的響應輸出也與輸入電流成線性關系,而且不同驅動器之間的輸出響應滿足線性疊加原理.從而能使用已經成熟應用于固態變形鏡的線性控制算法控制磁液變形鏡的鏡面面形.

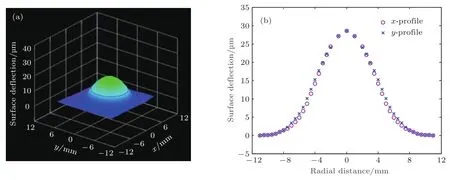
圖11 單個微線圈通15 mA電流所產生的鏡面面形(a)鏡面面形三維視圖;(b)鏡面面形的x和y軸向輪廓圖Fig.11.The surface de flection of a single coil with a current of 15 mA:(a)The three-dimensional display of the de flection obtained using the wavefront sensor;(b)x and y pro file of the surface de flection.

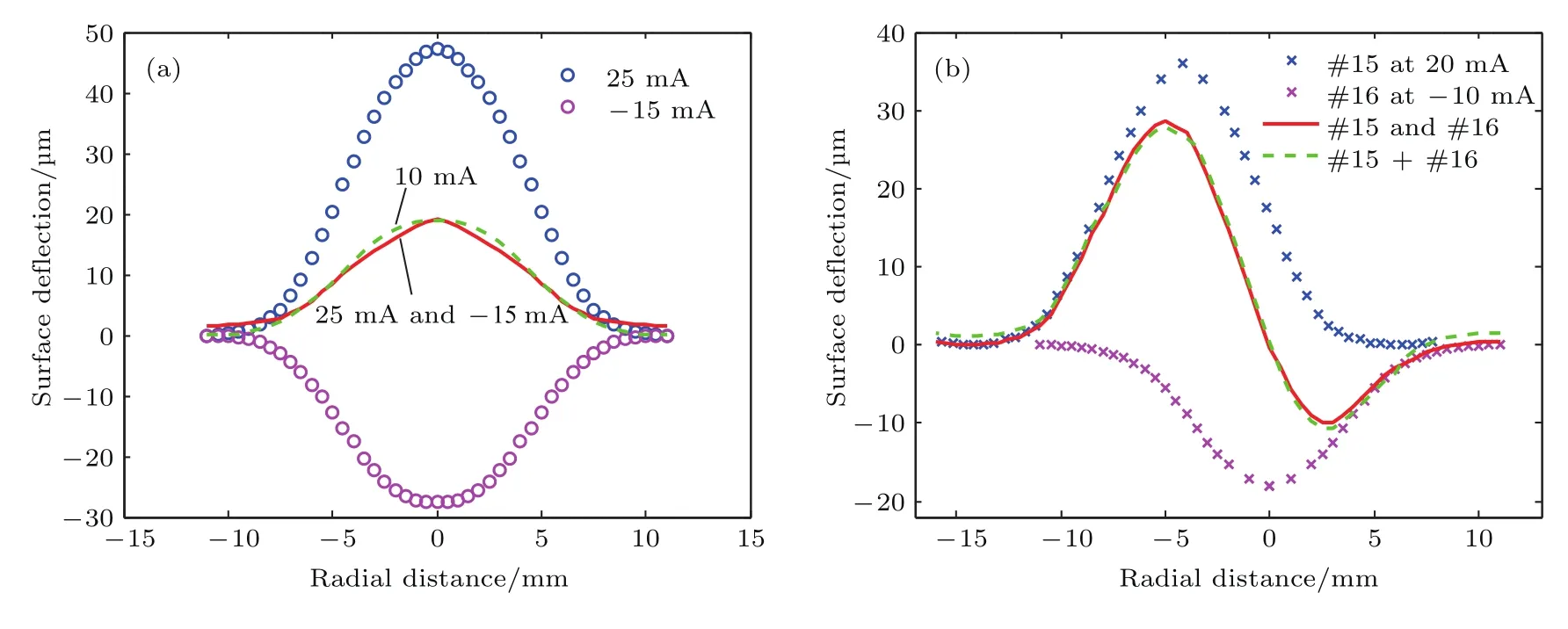
圖12 鏡面響應的線性疊加性(a)同一線圈輸入不同電流;(b)不同位置的線圈輸入不同電流Fig.12.Linear addition of surface de flection:(a)Linear relationship at a single coil with different currents;(b)linear relationship between two different coils.

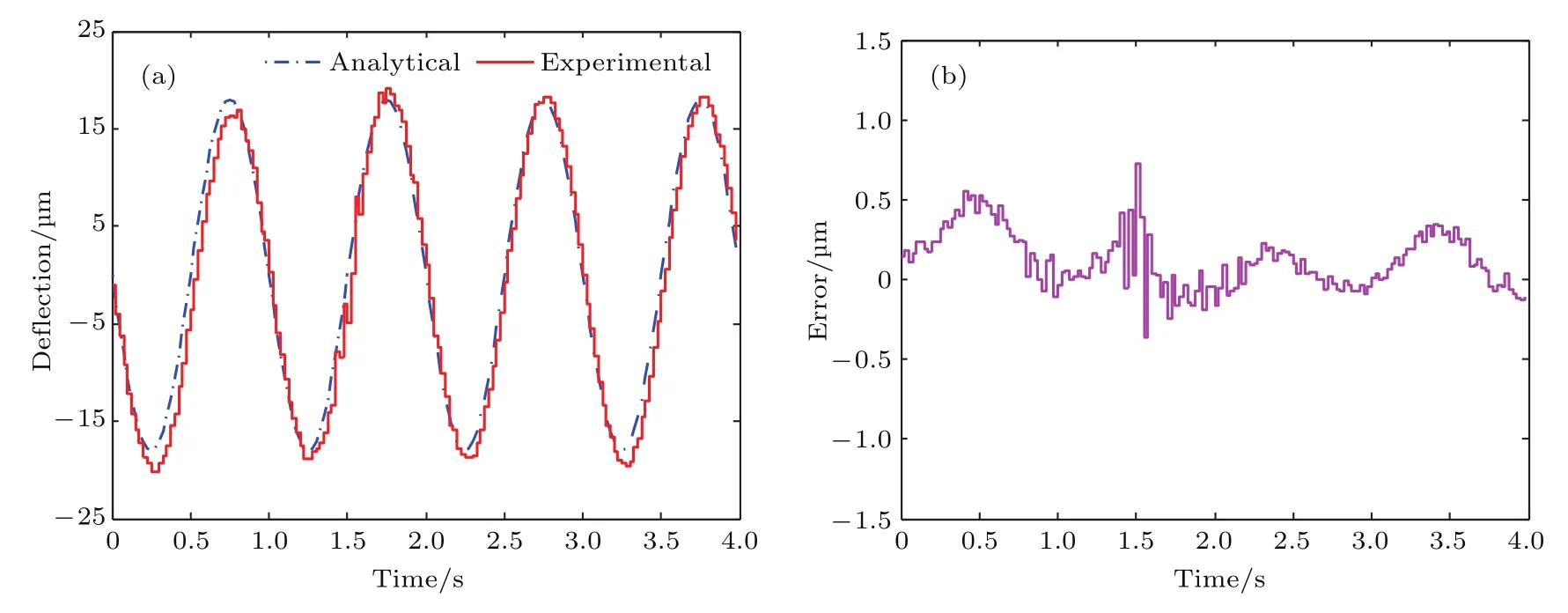
圖13 磁液變形鏡鏡面的動態響應(a)鏡面響應;(b)響應誤差Fig.13.Dynamic response of the magnetic fluid deformable mirror:(a)Surface de flection;(b)error.

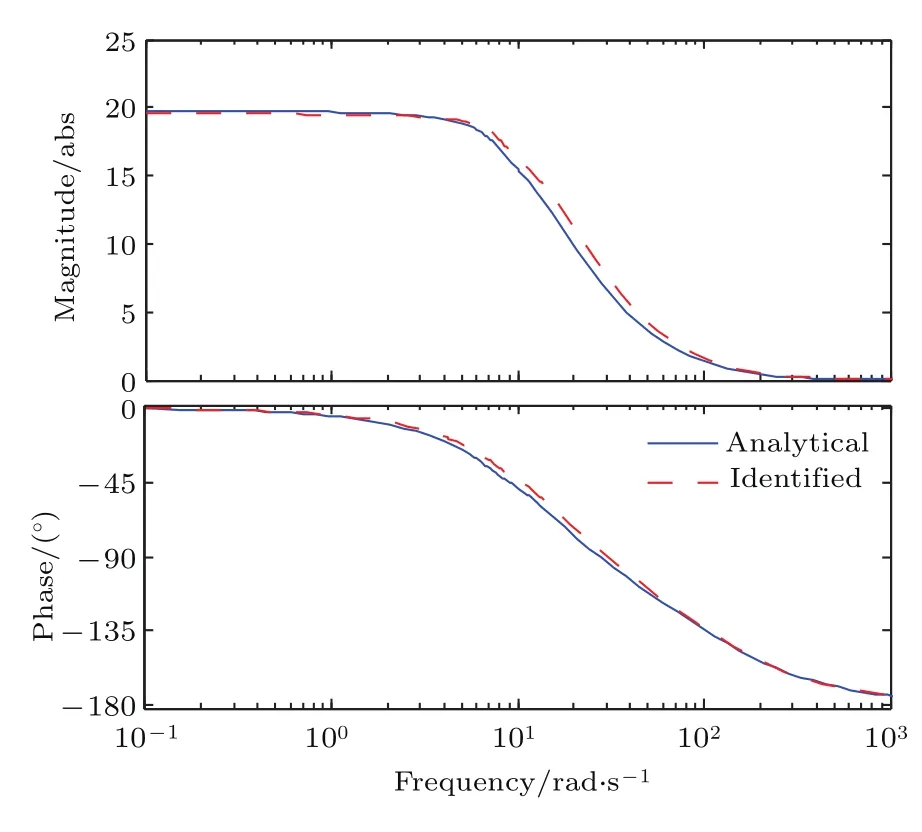
圖14 磁液變形鏡鏡面響應模型的伯德圖Fig.14.Bode plot of the magnetic fluid deformable mirror system.

為了驗證磁液變形鏡鏡面動力學性能,磁液變形鏡鏡面在正弦信號下的響應如圖13所示,其中輸入中心微線圈的正弦電流幅值為10 mA,頻率為1 Hz.圖13(a)中的紅色實線為磁液變形鏡實際響應曲線,藍色點劃線為理論推導模型的響應曲線.圖13(b)為鏡面實際響應與理論推導模型的響應誤差,誤差范圍在4.5%以內.此外,對磁液變形鏡鏡面在0 Hz到150 Hz隨時間變化的掃頻電流信號作用下的響應進行了實驗驗證.圖14所示紅色點劃線為磁液變形鏡實驗辨識模型的伯德圖,藍色實線為理論推導模型的伯德圖,由圖13和圖14可以看出基于理論推導模型的鏡面響應與實驗結果相符,說明磁液變形鏡的鏡面響應理論推導模型基本準確.

4.2 方形激光束聚焦實驗

為了驗證磁液變形鏡對激光束波前的控制性能,利用所搭建的自適應光學系統來控制磁液變形鏡產生拋物面形.由磁液變形鏡所產生的期望鏡面面形為,由方程(45)計算得到的電流i輸入到微線圈驅動器陣列中,圖15所示為波前傳感器記錄的磁液變形鏡所產生的鏡面拋物面形,從圖中可以看出拋物面的最大變形約為20μm,且面形同圖4的仿真結果比較符合.相對應在CCD相機中獲得的方形聚焦光斑如圖16所示,方形聚焦光斑的尺寸為480μm×480μm,包含了90%以上的激光源總能量,而且光斑強度分布均勻.實驗結果表明本文設計的方形磁液變形鏡可以產生期望的鏡面面形,并能有效地控制方形激光束從而獲得均勻的聚焦光斑,驗證了推導模型的準確性.如結合現有成熟的固態變形鏡鏡面控制算法可實時控制磁液變形鏡的鏡面面形,以獲得不同焦距的方形聚焦光,或用以糾正自適應光學系統中光束的時變像差.

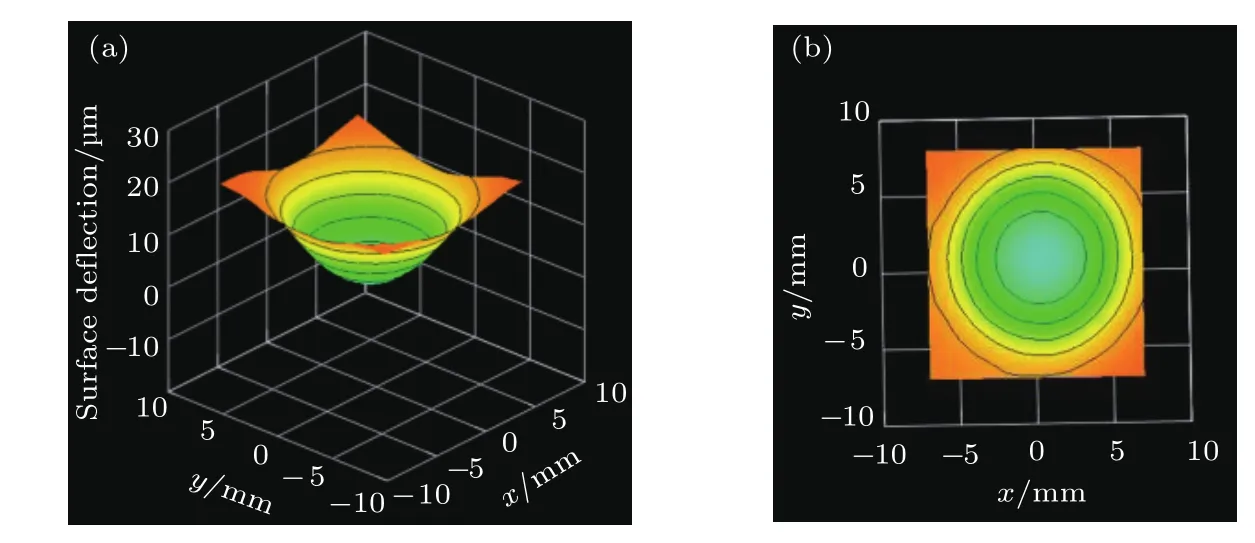
圖15 磁液變形鏡產生的拋物面鏡面面形(a)軸測圖;(b)俯視圖Fig.15.The parabolic shape from experimental result:(a)Isometric view;(b)top view.

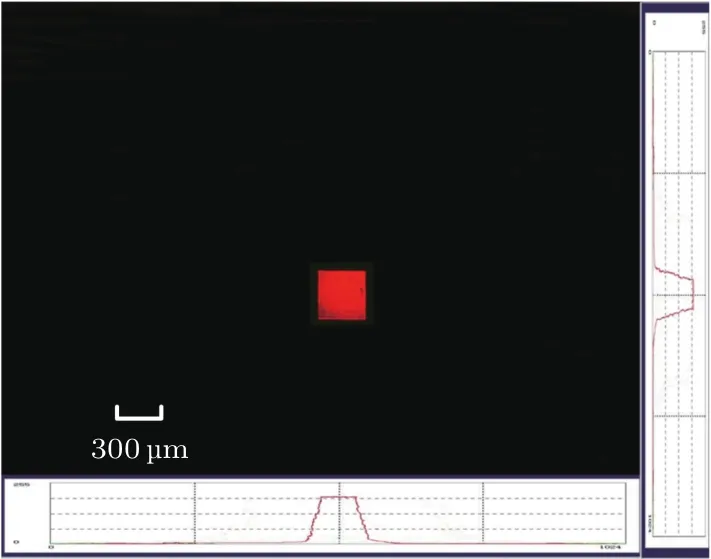
圖16 基于磁液變形鏡所產生拋物面獲得的光束聚焦光束Fig.16.Focused spot generated by parabolic shape of the magnetic fluid deformable mirror.

5 結 論

本文在磁性液體受重力場、電場和磁場多物理場耦合情況下,考慮磁液中的磁性納米顆粒相互之間的作用力和磁液受流體磁壓力、磁致伸縮壓力的影響,以方形微線圈陣列驅動的磁液變形鏡為例,運用Maxwell方程組和Laplace方程,在考慮磁液容器厚度的情況下,通過引入歐拉函數和分離變量的方法在笛卡爾直角坐標系中推導出了磁液變形鏡的鏡面動力學模型.然后基于推導的模型,設計了滿足光束波前控制要求的變形鏡結構和參數,并進行仿真驗證.最后搭建了基于磁液變形鏡的自適應光學系統,驗證了推導模型的準確性以及所設計磁液變形鏡鏡面響應線性度,實驗結果表明該磁液變形鏡能產生精確的鏡面面形并具有良好的激光束波前控制性能.

[1]Rosensweig R E 1985Ferrohydrodynamics(Cambridge:Cambridge University Press)pp1–64

[2]Wang A R,Xu G,Shu C J 2010Magnetic Fluid and Applications(Chengdu:Southwest Jiaotong University Press)pp1–20(in Chinese)[王安蓉,許剛,舒純軍 2010磁性液體及其應用 (成都:西南交通大學出版社)第1–20頁]

[3]Li D C 2010Theory and Applications of Magnetic Fluid Seal(Beijing:Science Press)pp38–68(in Chinese)[李德才 2010磁性液體密封理論及應用 (北京:科學出版社)第38–68頁]

[4]Papell S S 1965US Patent3 215 572

[5]Yuichi M,Hiroshi S,Hayato Y,Hidenori S 2015Procedia CIRP33 581

[6]Rajesh C S,Parsania M M 2013Am.J.Math.Stat.3 179

[7]Yao J,Chang J J,Li D C,Yang X L 2016J.Magn.Magn.Mater.402 28

[8]Mitamura Y,Yano T,Nakamura W,Okamoto E 2013Bio-Med.Mater.Eng.23 63

[9]Dave V,Virpura H A,Patel R J 2015 AIP Conf.Proc.1665 050139

[10]Nguyen N T,Beyzavi A,Ng K M,Huang X Y 2007 Micro fluid Nano fluid 3 571

[11]Liu J,Tan S H,Yap Y F,Ng M Y,Nguyen N T 2011 Micro fluid Nano fluid 11 177

[12]Brousseau D,Borra E F,Hubert J R,Parent J 2006 Opt.Express 14 11486

[13]Brousseau D,Borra E F,Thibault S 2007 Opt.Express 15 18190

[14]Borra E F,Brousseau D,Cliche M,Parent J 2008 Mon.Not.R.Astron.Soc.391 1925

[15]Iqbal A,Amara F B 2008 Int.J.Optomechatroni.2 126

[16]Ritcey A M,Borra E 2010 ChemPhysChem 11 981

[17]Lemmer A J,Griffths I M,GroffT D,Rousing A W,Kasdin N J 2016 Proc.SPIE 9912 99122K

[18]Dery J P,Brousseau D,Rochette M,Borra E F,Ritcey A M 2016 J.Appl.Polym.Sci.134 44542

[19]Wu Z Z,Kong X H,Wu J Q,Liu M,Xie S R 2016 Chin.J.Sci.Instrum.37 1509(in Chinese)[吳智政,孔祥會,吳君秋,劉梅,謝少榮2016儀器儀表學報37 1509]

[20]Wu Z Z,Kong X H,Zhang Z,Wu J Q,Wang T,Liu M 2017 Micromachines 8 72

[21]Bayanna A R,Louis R E,Chatterjee A,Mathew S K,Venkatakrishnan P 2015 Appl.Opt.54 1727

[22]Bastaits R,Alaluf D,Horodinca M,Romanescu I,Burda I,Martic G,Rodrigues G,Preumont A 2014 Appl.Opt.53 6635

[23]Du R Q,Zhang X J 2011 Opto-Electron.Eng.38 30

[24]Calero V,García-Martínez P,Albero J 2013 Opt.Lett.38 4663

[25]Yao K,Wang J,Liu X,Liu W 2014 Opt.Express 22 17216

[26]Peng F,Lee Y,Luo Z,Wu S 2015 Opt.Lett.40 5097

[27]Ghaffaria A,Hashemabadi S H,Bazmib M 2015 Colloid.Surface A 481 186

[28]Shi D,Bi Q,Zhou R 2014 Numer.Heat Tr.A:Appl.66 144

[29]Akhtar S N,Sharma S,Dayal G,Ramakrishna S A,Ramkumar J 2015 J.Micromech.Microeng.25 065001

[30]Jiao L,Cai J,Ma H H,Li G X,Shen Z W,Tang Z P 2014 Appl.Surf.Sci.301 481

[31]Marmo J,Injeyan H,Komine H,McNaught S,Machan J,Sollee J 2009 Proc.SPIE 7195 719507A

[32]Wu Z Z,Iqbal A,Ben Amara F 2013 Modeling and Control of Magnetic Fluid Deformable Mirrors for Adaptive Optics Systems(New York:Springer)pp99–115

[33]Caprari R S 1995 Meas.Sci.Technol.6 593

[34]Wu J Q,Wu Z Z,Kong X H,Zhang Z,Liu M 2017 Optoelectron.Lett.13 90

[35]Lu F,He Z W 2012 Comput.Simul.29 1006(in Chinese)[盧飛,何忠武 2012計算機仿真 29 1006]