融合密度峰值和模糊C-均值聚類算法*
任新維, 張桂珠
(江南大學 物聯網工程學院 輕工過程先進控制教育部重點實驗室,江蘇 無錫 214122)
0 引 言
各類聚類分析的算法中,模糊聚類可以描述樣本類的中介性,從而更客觀地反映真實的世界,成為非監督模式識別的一個重要分支,其中模糊C—均值(fuzzy C-means,FCM)聚類算法是運用最廣泛的模糊聚類算法[1~3],但算法也存在著很多不足,如:對初始值過于敏感,容易陷入局部最優,整體效率不高等[4,5]。密度峰值聚類[3](density peaks clustering,DPC)算法是Alex Rodriguez和Alessandro Laio提出的一種新的基于密度的聚類算法,其基本思想簡單且效率高,對于任意形狀的數據集,能夠快速發現其密度峰值點,但算法聚類效果在某種意義上依賴于用于計算局部密度的截斷距離dc,而文獻[6]并沒有給出dc的計算方法;其次,對同一個類存在多密度峰值的情況,該算法聚類效果并不理想。
針對FCM算法和DPC算法存在的上述缺點,本文提出了DPC-FCM算法。實驗結果表明DPC-FCM算法具有更好的聚類效果。
1 DPC算法及其改進
1.1 算法基本思想[6]
理想的類簇中心周圍有局部密度較低的相鄰點圍繞,且與更高密度的任何點有相對較大的距離。為了準確找到上述條件的類簇中心,需要計算每個數據點i的兩個量:局部密度ρi和數據點i到更高局部密度點j的最短距離δi,以刻畫聚類中心。ρi有Cut-off kernel和Gaussian kernel兩種計算方式,Cut-off kernel為
(1)
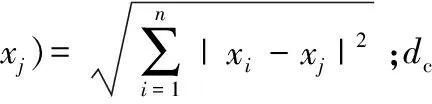
(2)
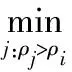
(3)
分別計算出樣本數據集中所有數據點xi的ρi,δi。然后再計算一個將ρ值和δ值綜合考慮的量γ
γi=ρiδi,i∈Is
(4)
將余下的數據點分配到與其距離最近且密度較其更高的點所屬的簇。然后算法定義每個簇的邊界區域密度ρb:屬于某個簇并且與屬于其他簇的數據點之間的距離小于截斷距離dc的數據點總數。密度較ρb高的點視為核心點,其余的點視為噪聲點,由此得到聚類的最終結果。
1.2 算法的局限性[6]分析
1)關于數據集規模的大小判斷沒有確切的衡量標準,導致樣本密度計算方式的選取可能影響聚類的結果。
2)如果有一個樣本數據的聚類中心歸類出現了錯誤,即導致最終的聚類結果千差萬別。
3)對于比較復雜的數據集,由于不同類簇之間密度可能會有較大的差異,此時DPC算法如果繼續在歐氏距離測度下進行聚類[7,8],取值不同的截斷距離dc就會產生不同的聚類結果,很容易得到錯誤結果。
1.3 DPC算法的改進
本文采用了一種新的自適應度距離來對DPC算法進行改進。在現有多種相似度度量中,自調節相似度[9]計算方法考慮到了鄰域數據分布對兩點相似度的影響,準確反映復雜結構數據集的分布特點
(5)
式中σi=d(si,sk),其中點sk為si的第K個近鄰點;σi為點si與sk的歐氏距離,根據文獻[9]令K=7,可以在高維數據的條件下得到較好的結果。在自適應相似度測度下查看Jain數據集,設點a處在高密度簇中而點c處在低密度簇中,顯然σa<σc,可以推出σaσb<σcσb,從而得到Aab>Abc,由此可以看出,采用自適應相似度的計算方法可以更好地度量不同密度簇之間點的相似度。本文將自適應相似度轉換為權值加入到歐氏距離公式中,生成了一種新的加權歐氏距離公式
(6)
式中Aij∈[0,1]為點i和點j的自適應相似度。
權值wi=1-Aij
(7)
在采用具有加權歐氏距離公式計算相似度后,各個對象之間的差異可以更準確地算出來,DPC算法可以基于此公式計算每個數據點的局部密度ρi和點i到局部密度更高點的最近距離 ,從而更準確地選取聚類中心點,提高聚類結果的準確率。
2 FCM聚類算法
FCM聚類算法描述為:
1)確定類的個數k,指數權重α,初始化隸屬度矩陣U(0)。令m=1表示第一步迭代。
2)計算聚類中心。給定C(m),計算U(m)。
3)重新計算隸屬度。給定U(m),計算C(m)。
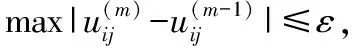
經過上述4步的多次迭代,可以得到最終的隸屬度矩陣U和聚類中心V,使得目標函數J(U,V)最小,再根據隸屬度矩陣U劃分樣本的最終分類。
3 DPC和FCM的融合算法
3.1 算法思想
算法分為2個階段:1)對每個數據計算兩個量ρi和δi,刻畫聚類中心,ρiδi值越大,該點越可能是聚類中心;2)運用標準的FCM算法進行迭代,獲得更好的聚類結果。
3.2 算法步驟
DPC-FCM算法總體如下:
階段一:執行DPC算法,確定初始聚類中心。
輸入:樣本數據集X
輸出:聚類中心ci(k)。
1)根據加權歐氏距離公式計算數據點之間的距離;
2)根據步驟(1)計算的m=n(n-1)/2個距離進行升序排列,設得到的序列為d1≤d2≤…≤dM,取該序列前2 %的數據,確定截斷距離dc;
3)在步驟(1)得出的距離基礎上,計算每個數據點的局部密度ρi和數據點到局部密度較其大且距其最近的點的距離δi;
4)計算γi=ρiδi,繪制決策圖,γ越大越有可能是聚類中心,由此得到ci(k)。
階段二:執行FCM算法。
輸入:迭代終止條件ε、模糊指數α、樣本數據集X、聚類中心ci(k);
輸出:隸屬度矩陣U、聚類中心C。
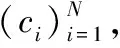
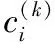
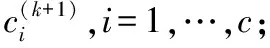
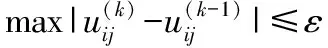
5)在完成上述4步的多次迭代后,根據最終得到的隸屬度矩陣U劃分樣本的最終分類。
4 實驗分析
為了證明DPC-FCM算法的有效性,采用Iris數據集和Wine數據集以及一組人工數據集Dataset對2種算法進行仿真實驗。使用MATLAB R213a進行實驗,表1為用于實驗的各個數據集構成。

表1 實驗數據集的構成描述
選取UCI中的Iris數據集進行驗證,此數據集包含150個樣本,來自于三類鶯尾花的花朵樣本,每一類包含50個樣本,每個樣本又包含4個屬性:sepal length,sepal width,petal width,petal length,利用改進的DPC算法選取聚類初始中心,然后與Iris實際的數據集進行對比,如表2所示。
可以看出,本文提出的改進算法選取的聚類初始中心與Iris數據集實際的中心非常接近,驗證了本文算法有效性。
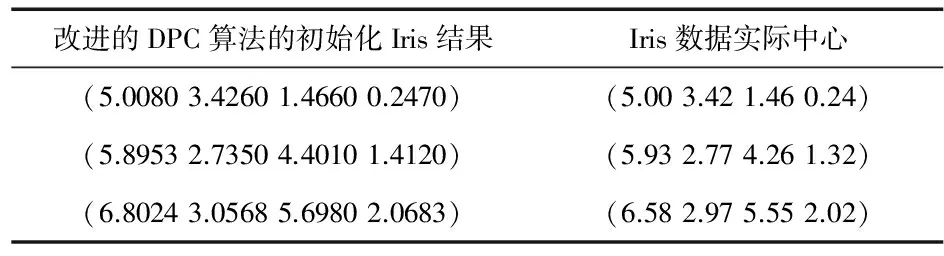
表2 初始聚類中心選取對比
在MATLAB仿真實驗中,對原始的FCM算法、DPC-FCM算法在Dataset,Wine,Iris數據集逐個進行50次試驗,計算聚類正確數的平均值,得到的實驗結果如表3所示。
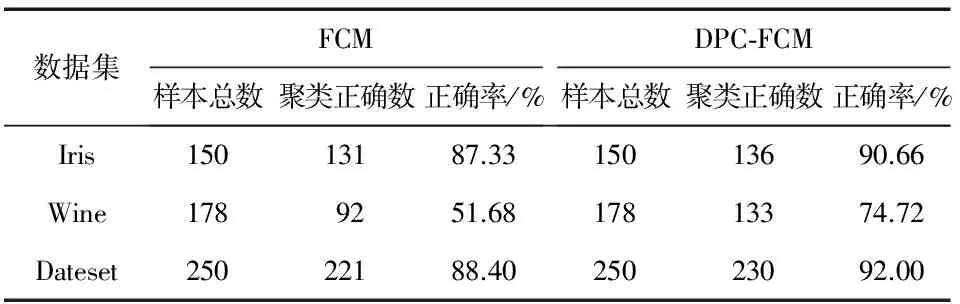
表3 聚類正確結果對比
可以看出,FCM算法對初始值比較敏感,聚類效果比較差,尤其是在Wine這種相對復雜的數據集上,隨機選取聚類中心導致最終聚類結果不理想;而DPC-FCM算法將DPC與FCM結合,利用了DPC算法的選取聚類中心較為準確的優勢,與傳統的FCM算法相比,聚類效果得到了提升。
圖1為對Iris,Wine和自定義數據集Dataset分別應用FCM,DPC-FCM算法的收斂速度對比。由圖可知,FCM尋優能力較差,過分依賴于初始的聚類中心。而DPC-FCM算法,能更準確地得到聚類中心,收斂速度更快,在尋優效果和全局搜索能力上均有較好的表現。
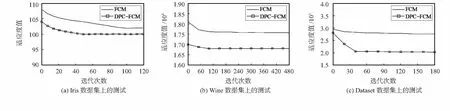
圖1 在不同數據集上的測試
采用F-measure指標、Rand指數和Jaccard系數對聚類結果進行評估。
F-measure計算公式如下
(8)
式中P為精確率;R為召回率。F-measure指標取值范圍為[0,1],值越大表明聚類效果越好。
此外,Rand指數可以反映出聚類結果與最初數據集之間的分布;而Jaccard系數越大代表聚類效果越好。
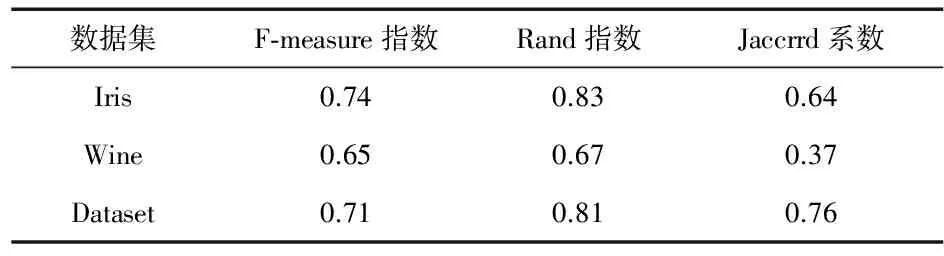
表4 FCM算法實驗結果
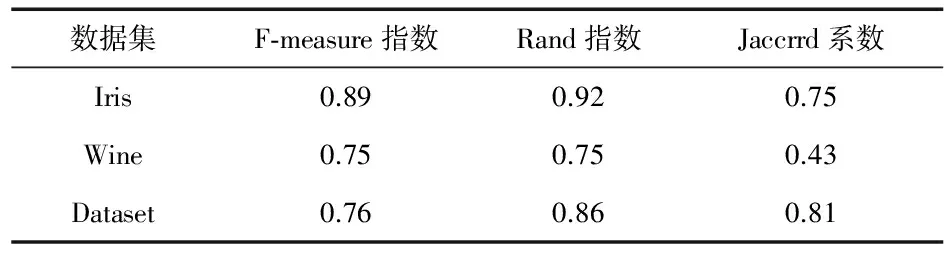
表5 DPC-FCM算法實驗結果
從表4和表5可以看出,DPC-FCM算法的聚類結果優于FCM算法。
5 結 論
通過實驗數據的分析可知,DPC-FCM算法提高了聚類正確率、全局收斂速度和優化精度,有效地提高了聚類的穩定性和準確性。
[1] 付爭方,朱 虹.基于模糊理論的低照度彩色圖像增強算法[J].傳感器與微系統,2014,33(5):121-124.
[2] 張國鎖,周創明,雷英杰.改進FCM聚類算法及其在入侵檢測中的應用[J].計算機應用,2009,29(5):1336-1338.
[3] Rodriguez Alex,Alessandro Laio.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.
[4] Zelnik-Manor L,Perona P.Self-tuning spectral clustering[J].Advances in Neural Information Processing Systems,2004,17:1601-1608.
[5] 李文杰,廖曉緯,束仁義,等.基于ZigBee和模糊C均值聚類算法在火警中的應用[J].傳感器與微系統,2012,31(10):143-152.
[6] 楊 燕,靳 蕃,Kamel M. 聚類有效性評價綜述[J].計算機應用研究,2008,41(6):1631-1632.
[7] 韓曉慧,王聯國.一種基于改進混合蛙跳的聚類算法[J].傳感器與微系統,2012,31(4):137-139.
[8] 高孝偉.權熵法在教學評優中的應用研究[J].中國地質教育,2008,17(4):100-104.
[9] 華 漫,李燕玲,魏永超.基于自適應相似度距離的改進FCM圖像分割[J].電視技術,2016,40(2):33-36.

