軌道安全監測中傳感器優化配置研究
劉 超
(中鐵第一勘察設計院集團有限公司,西安 710043)
隨著城市建設加快,地鐵、市域鐵路作為城市交通大動脈,扮演著越來越重要的角色。然而,客運量增加、列車往返碾壓和復雜運營條件的不間斷作用,使軌道結構不可避免地出現疲勞損耗和局部破損。這些隱患不會立即破壞整體系統,但對整個結構的安全已構成潛在威脅,隱患不斷累積會導致局部破損愈演愈烈,輕則影響線路狀態劣化乘車體驗,重則造成脫軌,車毀人亡[1]。目前對于軌道系統的監測一般采用夜間天窗點人工上道巡檢和周期性車載檢測[2],無法實時掌控軌道狀態,所以結構安全監測意義重大,也是未來軌道結構安全評估的重點環節。
對于軌道監測系統,傳感器布置的越多,得到的監測數據就越詳細,從而更有利于分析軌道結構的服役狀態。但實際情況中,綜合考慮經濟性、線路運營安全性等因素,鋼軌監測測點無法達到較高密度,監測時傳感器間距遠大于期望值,所以在進行傳感器布置時,如何選擇測點位置、安裝間距,如何保證監測的準確性、經濟性一直是困擾和制約軌道交通行業結構長期安全監測技術發展的難題。
國內很多學者對軌道結構的監測技術進行了研究,但主要都集中于高速鐵路[3-5];除此之外,軌道結構監測中傳感器監測位置的選擇和監測方案的評價方法還沒有形成體系[6-10]。因此,如何將有限的傳感器配置在最優位置,通過Ω區域內布置的n個傳感器達到技術和經濟的最優組合,發展科學、經濟和合理的軌道結構安全監測技術是當前的研究重點[11]。
1 優化準則
目前用于傳感器測點方案優化的常用方法有:模態動能法(MKE)、有效獨立法(EI)、遺傳算法(GA);常用的優化準則有傳遞誤差最小準則、插值擬合準則和模態應變能準則等[12]。軌道系統是長條帶狀結構,在車輛、溫度、基礎變形等荷載的組合作用下受到剪力、溫度力、附加力等力的作用,無法用一個表達式來進行全面描述,因此可以采取插值擬合誤差最小準則針對不同類型監測指標來配置傳感器。
傳感器監測數據是以一種離散點的形式來呈現的數據結果,將這些離散點連起來會形成一條由多線段組成的連續折線。當測點足夠多時,多測點組成的測點折線和鋼軌受力曲線便可達到高擬合狀態,這樣的測試結果真實可信,監測效果也可達到最好狀態。
為了分析傳感器的位置、數量及擬合方法的精度,可利用結構分析軟件(如ANSYS或其他結構計算軟件)計算出額定荷載作用下結構的實際效應值,再通過調整傳感器布置位置得到輸出值擬合效應曲線,最后根據誤差最小準則,在滿足經濟性前提下得到傳感器布置方案[14-15]。
2 數學模型
采用插值誤差最小準則配置傳感器的數學模型為:設目標值由直接測量的鋼軌參數x1,x2,…,xn決定,δ1,δ2,…,δn分別為其誤差,Δy代表由δ1,δ2,…,δn引起的誤差,則有
y+Δy=f(x1+δ1,x2+δ2,…,xn+δn)
(1)
將(1)式按泰勒級數展開,并略去高階無窮小,得
(2)
那么最大誤差為
由上述算式可知,傳感器最優方案的選擇,不僅僅是數目n的選擇,還包括給定區域上的位置選擇[12]。
選定一種傳感器的布置方式,即當區域和數量n給定時,存在一個Δymax,按照誤差最小準則,傳感器布置的最優目標為
min(Ω,n)=(Δymax)
(3)
3 測點方案優化體系
3.1 測點選擇
軌道結構的受力是影響其強度和穩定性的主要因素,也是無縫線路檢算的重要指標。鋼軌應力的監測數據可以直接反映出結構的受力情況,從而判斷出安全服役狀態[13]。而在所有軌道結構中,橋上渡線道岔承受復雜的運行荷載和環境作用,具有最特殊的力學特性。以12號渡線道岔為例對測點優化進行研究,并建立精細化空間耦合模型。12號渡線道岔及建立的ANSYS模型如圖1所示。
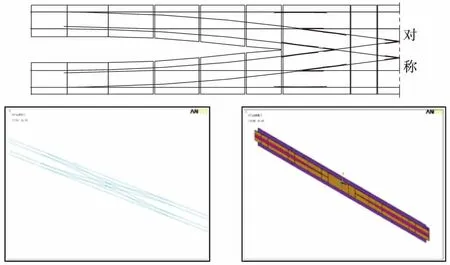
圖1 12號渡線道岔及空間模型
根據道岔敏感區域的初步分析結果可知,道岔鋼軌的最大縱向力出現在基本軌上,因此選擇橋上渡線道岔基本軌縱向力為研究對象進行測點布置和優化研究。由模型分析得到的直基本軌縱向力如圖2所示。
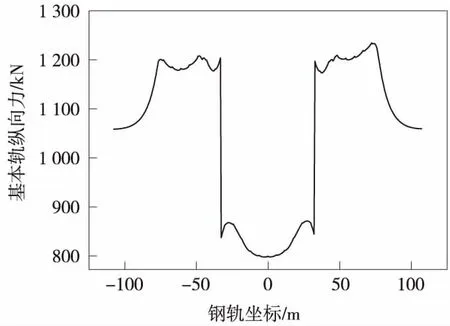
圖2 離散測點縱向力
在基本軌上布置傳感器,即通過布點使傳感器得到的縱向力來描述道岔受力曲線,監測縱向力的同時得到鋼軌的受力狀態。在選擇傳感器位置時利用曲線斜率的變化量(二階倒數)作為評價數據間相關性的指標。圖2中相鄰兩點QiQi+1{(xi,yi),(xi+1,yi+1)}的斜率為ki,隨后相鄰數據長度兩點Qi+1Qi+2{(xi+1,yi+1),(xi+2,yi+2)}的斜率為ki+1,兩個斜率之差的絕對值|Δk|可用來描述點Qi+1對于曲線的貢獻值。貢獻值越大,認為它對描述曲線線型具有更明顯的作用。
在布設測點時即可選擇曲線貢獻值所對應較高的測點。如圖3所示,k1,k2兩點的貢獻值最大,當鋼軌縱向力如圖中所示曲線時,測點只用布置端點、k1、k2四個即可,4個測點數據所連曲線與原曲線擬合度最高,誤差最小,傳感器布置目標達到最優。
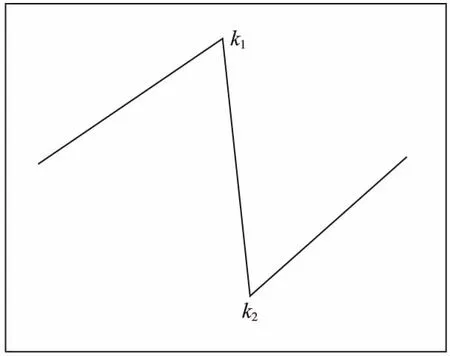
圖3 曲線貢獻值
通過Matlab將鋼軌坐標和對應縱向力數據輸入,可自動計算出對應鋼軌坐標的曲線貢獻值,部分鋼軌單元貢獻值如表1所示,繪制三維圖表如圖4所示。其中X軸表示鋼軌位置坐標,Y軸表示對應單元的縱向力,Z軸為曲線貢獻值。從圖4中可知,曲線拐角處Z軸數據明顯變高,說明曲線在此處斜率的變化量明顯增大,是曲線高貢獻值點。在曲線比較圓滑的地段Z軸高度趨近于零,曲線斜率變化較為緩慢,縱向力變化較為頻繁地段Z軸高度呈現鋸齒形波動變化,說明此處縱向力需要進行連續監測,同時也對敏感區域、敏感點尋找方法進行了驗證。在進行測點布置時,按照敏感區域范圍內鋼軌單元個數,每次選擇1%的數組進行繪圖。12號橋上渡線道岔直基本軌包含347個鋼軌單元,每次增加4個測量單元。選擇測量單元坐標時按照貢獻值由大到小依次選取。選取測點位置后再與起點、端點坐標數組依次連接構成傳感器監測布設曲線。分步次排列的測點曲線如圖5所示。
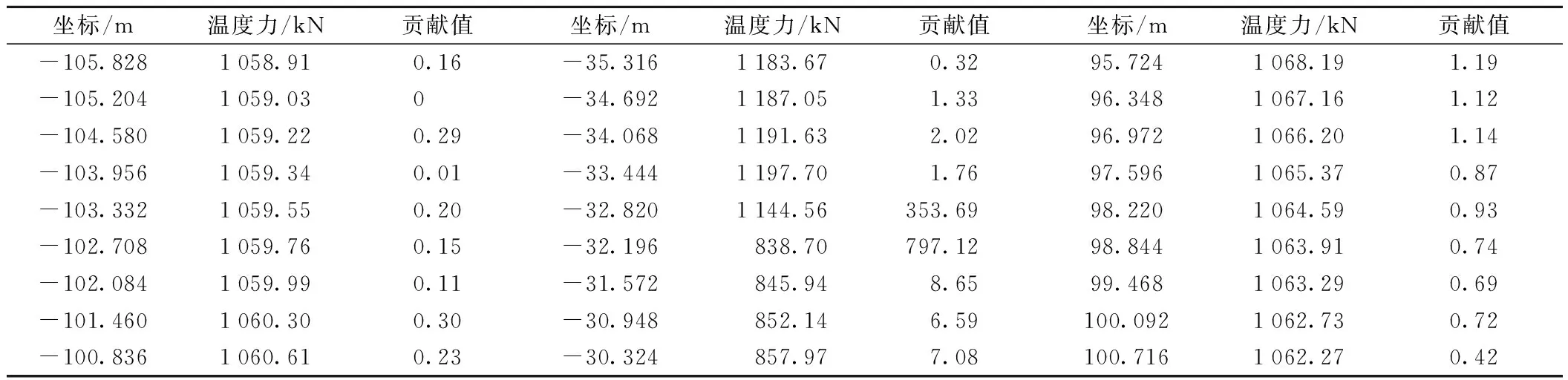
表1 鋼軌縱向力測量單元貢獻值(部分)
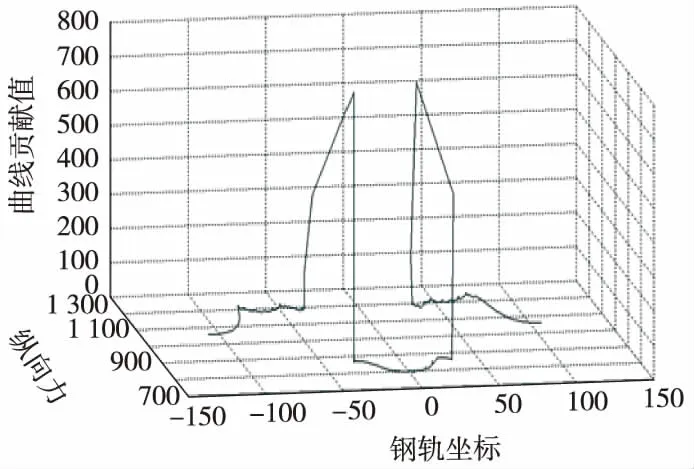
圖4 鋼軌單元和對應縱向力和曲線貢獻值
從圖5可知,在第4次選擇位置后繪制的測點曲線已經能夠極好地描述鋼軌縱向力的線型。第3次選擇位置后繪制的測點曲線可基本滿足長期監測需求,第1、2次選擇位置后繪制的測點曲線不能保證監測的準確性。
3.2 方案選擇
按照誤差最小準則,由傳感器測得的鋼軌縱向力與剛度、應變量的關系式:f(x)=EIε(x),可得到測點優化布置的目標函數

(4)
式中,EI為剛度;ε為傳感器測得的應變量;f(x)為鋼軌縱向力;(Ω,n)為最優傳感器布置方案。
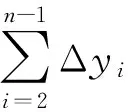
繼續進行6次測點選取,求得誤差比率后做散點圖并進行線性擬合,結果如圖6(a)所示。擬合曲線Adj. R-Square=0.987 75,表明具有極高精確度。
當所有鋼軌單元都被布置傳感器時,誤差比率趨近于零,此時的誤差比率散點圖和擬合曲線如圖6(b)所示,其擬合曲線Adj. R-Square=0.987 75,擬合曲線公式相同。
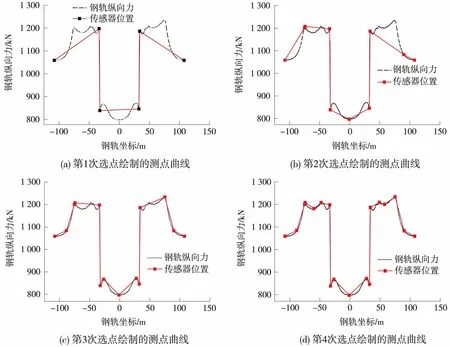
圖5 不同步次繪制的測點曲線
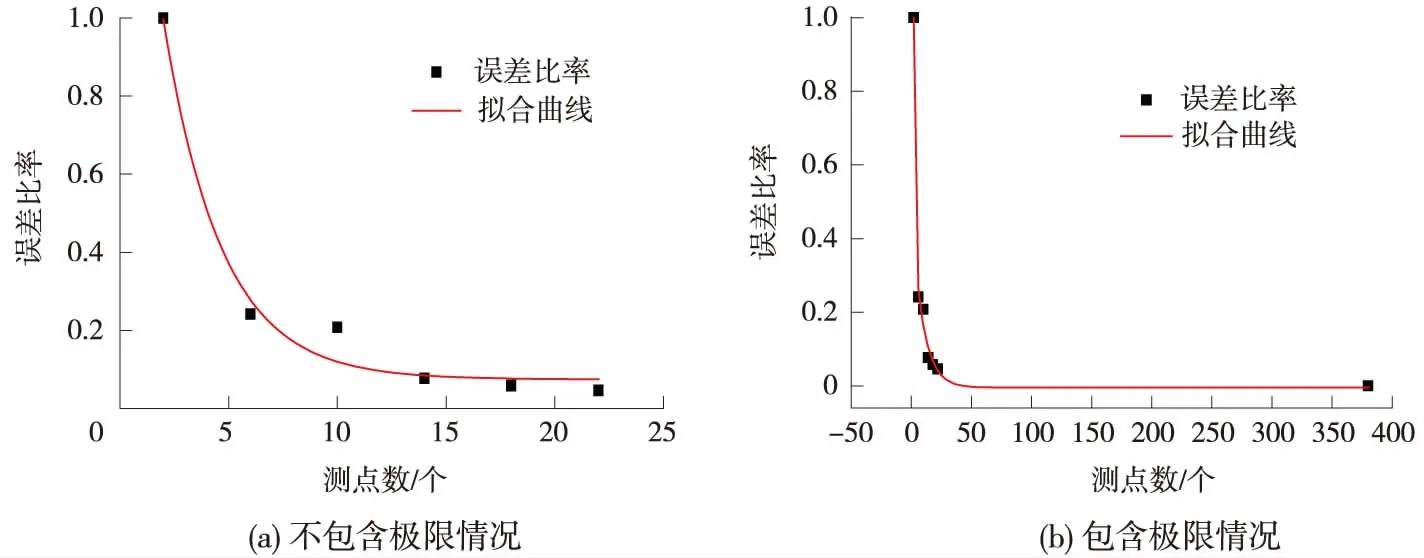
圖6 誤差比率散點
通過兩次繪制的散點圖和擬合曲線可以發現,隨著測點個數的增加,誤差比率以指數形式遞減,即增加傳感器個數后帶來的測點準確性收益逐步減小。由圖6(a)可知,第3次的誤差比率已經達到較好狀態,此數值在圖6(b)中處于拐點底部。考慮安全富余量,選取0.08為誤差比率限值(略小于第3次對應數值),此時認為測點方案既滿足了準確性,又保證了經濟性。
以誤差比率限值來看,第4次增加測點時形成的布置方案滿足了安全評價標準。從圖7可以看出,在部分區段內由于數值波動較大,設置的傳感器個數較多,但縱向力數值相差不大。從經濟性的角度出發,可考慮減少這些區域的傳感器。圖8為修改后的方案,新的方案刪減了部分密集區域的傳感器,此時誤差比率為0.08,滿足監測要求。

圖7 修改前監測方案
圖8和表2所示即為橋上渡線道岔直基本軌縱向力監測傳感器布設方案。道岔結構其余部分敏感指標的傳感器測點布置方案確定方式與鋼軌縱向力指標相同,首先通過模型分析確定不同結構單元的受力數值,在此基礎上通過貢獻值的思路確定監測單元,最后通過基于誤差最小準則原理優化監測方案,將誤差控制在合理范圍內,并保證經濟合理性。

圖8 修改后監測方案
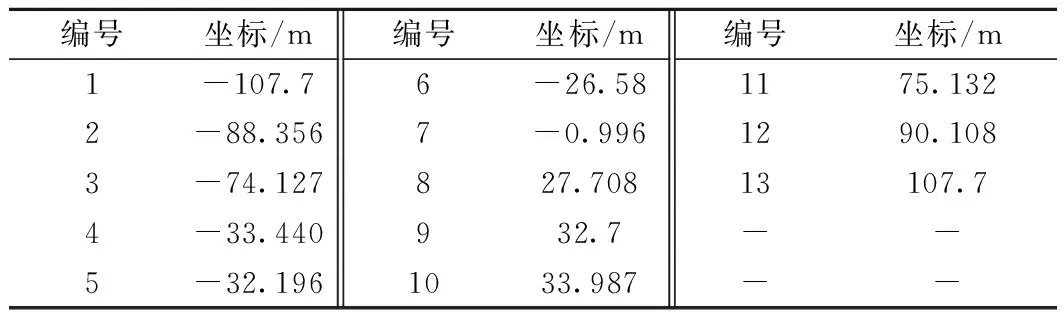
編號坐標/m編號坐標/m編號坐標/m1-107.76-26.581175.1322-88.3567-0.9961290.1083-74.127827.70813107.74-33.440932.7--5-32.1961033.987--
4 結論
以橋上12號渡線道岔力學模型為基礎,從實際的溫度荷載、橋梁伸縮條件出發,建立了鋼軌應變傳遞誤差最小的目標函數,完善了傳感器測點選擇依據,形成了較為完備的測點布置、優化及評價體系,保證了監測方案的經濟性、合理性。主要的研究結論如下。
(1)傳感器布設位置的確定,是以扣件為節點將鋼軌劃分為單元,再通過建立空間耦合模型得到的數據曲率,根據“貢獻值”大小依次選擇。
(2)在方案比選過程中,隨著傳感器測點數量增加,監測方案的誤差比率減小,但在“拐點”后增加單個傳感器帶來的收益降低,本文決定傳感器布設方案的擬合曲線“拐點”值為0.08。
(3)誤差最小準則能夠用來評價傳感器布設方案的合理性,使選擇方案既能保證監測數據的準確性,又能保證監測方案的經濟性。
(4)鋼軌位移、附加力等指標監測的監測方案也可以通過測點選擇、誤差求解、方案選定的流程來確定。
[1] 劉艷,劉貴杰,劉波.傳感器優化布置研究現狀與展望[J].傳感器與微系統,2010(11):4-6,13.
[2] 雷曉燕,王全金,圣小珍.城市軌道交通環境振動與振動噪聲研究[J].鐵道學報,2003(5):109-113.
[3] 王玉澤,王森榮.高速鐵路無砟軌道監測技術[J].鐵道標準設計,2015(8):1-9.
[4] 張政.光纖光柵傳感技術在高速鐵路軌道狀態監測中的應用[J].鐵道建筑,2016(5):77-81.
[5] 蔡小培,高亮,劉超,等.高架站無砟軌道道岔監測數據管理信息系統[J].鐵道工程學報,2016(1):52-57.
[6] 張明聚,王志剛.電阻應變式位移傳感器在軌道動態位移測試中的應用[J].石家莊鐵道學院學報,1994(1):59-64.
[7] 張兆亭,閆連山,王平,等.基于光纖光柵的鋼軌應變測量關鍵技術研究[J].鐵道學報,2012(5):65-69.
[8] 何浩祥,閆維明,張愛林.面向結構健康監測的傳感器數量及位置優化研究[J].振動與沖擊,2008(9):131-134,188.
[9] 張曉麗,梁大開,崔東輝,等.健康監測系統中光纖傳感器網絡優化布置研究[J].光電子·激光,2014(9):1754-1758.
[10] 盧偉,滕軍.基于數據融合的傳感器優化布置方法[J].振動與沖擊,2009(9):52-55,213.
[11] 梁鵬,李斌,王曉光,等.基于橋梁健康監測的傳感器優化布置研究現狀與發展趨勢[J].建筑科學與工程學報,2014(1):120-129.
[12] 譚冬蓮,肖汝誠.橋梁監測系統中梁橋靜力應變傳感器的優化配置[J].長安大學學報(自然科學版),2007(5):66-69.
[13] 蔡小培,高亮,林超,等.京滬高速鐵路高架站軌道系統長期監測技術[J].鐵道工程學報,2015(5):35-41.
[14] 譚冬蓮,肖汝誠.基于Levenberg-Marquardt算法的橋梁結構靜力參數識別[J].交通運輸工程學報,2005,5(3):56-59.
[15] 譚冬蓮,肖汝誠.橋梁監測系統中復雜結構的靜力應變傳感器優化配置方法[J].公路,2006(6):105-108.

