反應擴散模型在圖靈斑圖中的應用及數值模擬?

張榮培 王震 王語 韓子健

1)(沈陽師范大學數學與系統科學學院,沈陽 110034)

2)(山東科技大學數學與系統科學學院,青島 266590)

(2017年8月6日收到;2017年11月6日收到修改稿)

1 引 言

斑圖是在空間或時間上具有某種規律性的非均勻宏觀結構,普遍存在于自然界.1952年,著名的英國數學家圖靈把他的目光轉向生物學領域,用一個反應擴散系統成功地說明了某些生物體表面圖紋產生的原理[1].圖靈從數學角度表明,在反應擴散系統中,穩定狀態會在某些條件下失穩,并自發產生空間定態圖紋,此斑圖通常稱為圖靈斑圖.

經過多年的研究,各界學者利用反應擴散系統預測得到了更多的圖靈斑圖,在理論和實驗方面取得了許多重要成果.他們證實了化學系統中圖靈斑圖的形成[2],討論自催化反應中的動力學行為,探討此類耦合反應擴散體系中影響圖靈斑圖的因素[3].給出Gray-Scott模型、Brusselator模型等系統擴散引起不穩定的數學機理[4],并描述了Gierer-Meinhardt,Lengyel-Epstein等模型的某些動力學行為(性質)[5,6].最近幾年,圖靈斑圖在實驗方面取得一系列最新的進展,Copie等[7]運用實驗在一個雙穩態被動非線性共振器中探討了圖靈調制和法拉第參數不穩定性的相互作用;Tompkins等[8]利用微流體化學室證實圖靈理論體系,并觀測到第七種時空模式;Lacitignola[9]研究了圖靈不穩定現象的發生條件,論述了具體形態的電化學反應擴散模型在一個球面上的圖案形成的特性;Gaskins等[10]在二氧化氯碘丙二酸反應實驗中,通過添加鹵化鈉鹽溶液得到新的圖靈斑圖.

在這些系統中存在兩種化學反應物質,它們不僅能相互作用,而且還能進行獨自擴散.事實上,圖靈斑圖的產生對應的是一個非線性反應動力學過程與一種特殊擴散過程的耦合.這個特殊的擴散過程由于兩種因子的擴散速度不同會發生失穩,這就是圖靈斑圖產生的機理.在數學上,圖靈斑圖可以用無量綱化的反應擴散方程組描述[11],即

式中u和v是系統變量,分別代表參與化學反應的兩種物質的濃度;c和d是擴散系數,t是時間變量,f(u,v)和g(u,v)表示反應項.設?為RN中帶有光滑邊界的有界區域,?=[0,a]×[0,b],邊界為??,邊界條件為齊次Neumann邊界條件,即其中n表示邊界上單位外法向.

由于(1)式為耦合的非線性反應擴散方程,很難得到其精確解.近年來,許多學者用有限差分方法、有限元方法、譜方法等[12?14]多種數值方法求解(1)式,這些方法各有特點.相比于有限元方法和有限差分方法的低階精度,譜方法[14]僅用少量的節點,采用Legendre,Chebyshev等適合的正交多項式離散即可達到指數階收斂的譜精度.圖靈斑圖在空間上的結構具有一定的規律,且解比較光滑,因此采用譜方法離散是可行的.常用的譜配置方法主要有Fourier配置法[15],Chebyshev配置法[16],Hermite配置法等[17].由于本文考慮的(1)式邊界條件為齊次Neumann邊界條件,因此采用Chebyshev配置方法求解(1)式.

對(1)式進行空間離散后,得到的是剛性的非線性常微分方程組(ODEs).顯式時間離散方法雖可以用迭代的方法求解,但其對時間步長有嚴格的約束;隱式方法雖然可以允許大的時間步長,但是對于階數非常大的非線性方程組的求解問題十分復雜,這對于全隱式方法來說是一個巨大的挑戰.由于譜配置法所得到的譜微分矩陣是滿的,顯然利用追趕法等代數線性方程組的快速解法是不合適的,因此交替方向隱式方法在這里并不適用.本文采用緊致隱積分因子(compact implicit integration factor,cIIF)方法求解ODEs.2006年Nie等[18]以隱積分因子(IIF)方法為基礎發展了cIIF方法.傳統的隱積分因子方法在求解高維問題時,離散矩陣的指數運算的存儲量和運算量非常大,導致運算速度緩慢.緊致隱積分因子方法[19]通過引入離散矩陣的緊致表達式并在各個方向進行矩陣的指數運算,使得中央處理器(CPU)的存儲大大降低,計算速度也得到了顯著提高.

本文內容安排如下:第2節對反應擴散方程組進行線性分析,通過特征值解釋圖靈斑圖的數學機理,然后以Gierer-Meinhardt模型為例分析系統處于穩定狀態和不穩定狀態時各參數需要滿足的條件,進而探索斑圖形成需要滿足的條件;第3節研究數值方法,在空間離散條件下采用Chebyshev譜方法,時間離散條件下采用緊致隱積分因子方法,用MATLAB進行編程求解;第4節給出大量數值實驗并對理論分析結果進行驗證.

2 圖靈斑圖的形成

2.1 斑圖形成的數學機理

首先考慮(1)式沒有擴散項,假設存在惟一的均勻定態解(u0,v0),即常數u0,v0滿足

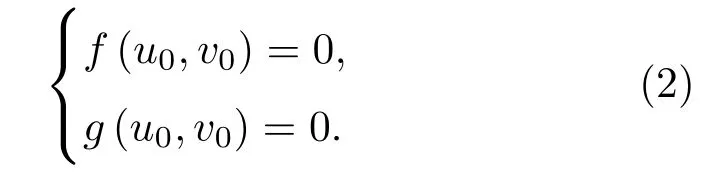
令U=u?u0,V=v?v0,并在(u0,v0)處線性化后得到如下系統:

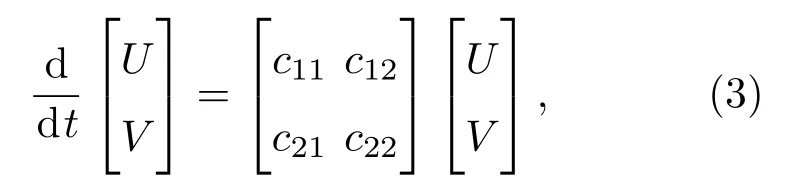
式中c11=fu(u0,v0),c12=fv(u0,v0),c21=gu(u0,v0),c22=gv(u0,v0).均勻定態解(u0,v0)在沒有擴散時是穩定的,這等價于相應的特征值問題的矩陣的特征值實部是負數.

考慮加入擴散項后的反應擴散方程組((1)式).如果此時產生斑圖,即(u0,v0)是不穩定的,要求特征值有正實部.所謂不穩定,體現為兩種反應物的擴散速度不同,從而引起失穩.對(1)式作線性化處理,研究特征值正實部引起的線性不穩定性,進而推導出原方程的不穩定性.對均勻定態解(u0,v0)作一個微擾,可得線性微擾方程為

求解如下方程可得相應的特征值:

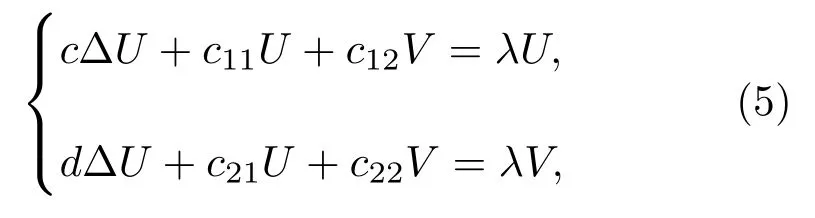
式中λ為特征值.只要(5)式中的特征值有正實部,則(u0,v0)對于(1)式是不穩定的.考慮到齊次Neumann邊界條件,得到(5)式所對應的特征值為

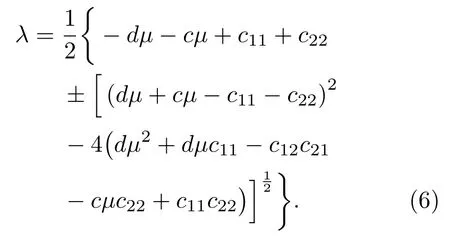
具體推導過程見附錄A.

2.2 Gierer-Meinhardt模型

生物的發育過程是復雜的,其中重要的是形態形成階段,與之對應的是生物體內器官的形成.由于該階段的重要性,漸漸形成一個新的領域——形態學,主要研究導致細胞分化和定位因素的濃度對組織器官的影響.Gierer-Meinhardt模型是由Gierer和Meinhardt在研究激活物和抑制劑兩種不同物質的產生和擴散時建立的[20],之后Gierer和Meinhardt利用數值方法導出一維和二維空間區域中上述系統產生多樣斑圖的條件.Gierer-Meinhardt模型被廣泛應用于形態形成過程中一些基本現象的研究,最近的一些工作可以參見文獻[21—23].

以Gierer-Meinhardt模型為例,結合上述理論分析,計算產生斑圖時需要滿足的條件.取(1)式中

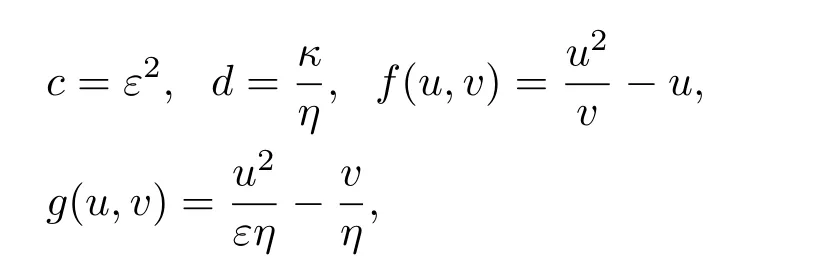
其中系數κ,η,ε為系統的控制參數,固定η=0.1,ε=0.04.由此得到線性化系統(3)式中的系數為

易得該系統的特征值為λ1=?1.2984,λ2=?7.7016,此時系統是穩定的.

加入擴散項后,原方程組對應的特征問題為

相應的特征方程為

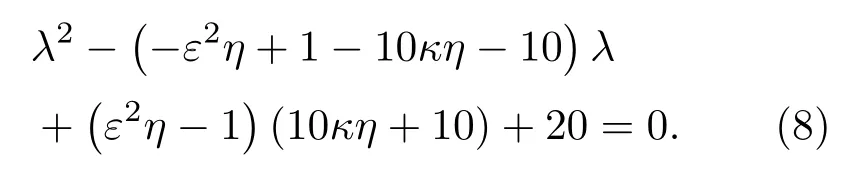
為使(8)式含有正實部的特征值,需要考慮兩種情況.

第一種情況是兩個特征值異號,則應滿足

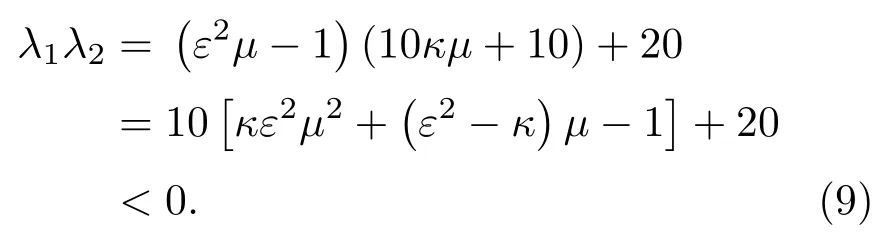
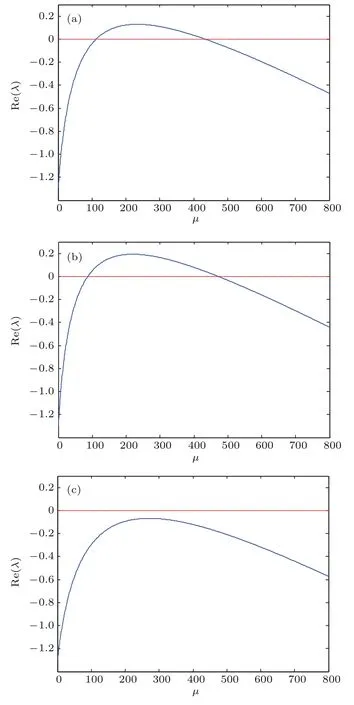
圖1 特征值的實部Re(λ)隨參數的變化 (a)κ=0.0128;(b)κ=0.0152;(c)κ=0.008Fig.1.Real part Re(λ)of eigenvalues varying with parameters:(a)κ=0.0128;(b)κ=0.0152;(c)κ=0.008.

第二種情況是兩個特征值都是正的,應滿足此時κ無解.

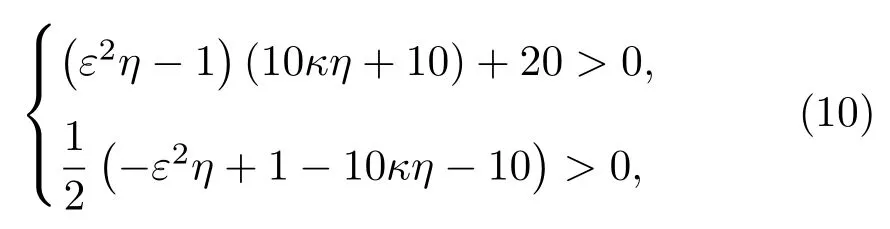
由于反應擴散方程組聯系于解析半群,所以線性化后的正實部特征值引起的不穩定性可以推導出原方程組的不穩定性.故當κ＞κ0=0.0093248時,系統處于不穩定狀態,因而系統能夠產生斑圖.特征值的實部Re(λ)在參數κ取不同值時的變化如圖1所示.

從圖1可以看出,當κ= 0.0128＞κ0和κ=0.0152＞κ0時,特征值的實部會出現正值,此時系統不穩定;當κ=0.008＜κ0時,特征值的實部始終為負,系統最后會達到穩定狀態.第3節將用數值算例驗證該結論.

3 數值方法

3.1 Chebyshev譜配置法

將求解區域[?1,1]2離散為Gauss-Lobatto網格,即

其中Nx和Ny是正整數.對于一般的求解區域?=[a,b]×[c,d],可以采用公式

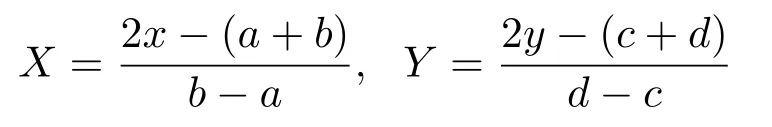
將區域轉化為[?1,1]2.在網格Th中將u(x,y)數值解定義為矩陣形式,U∈R(Nx?1)×(Ny?1),

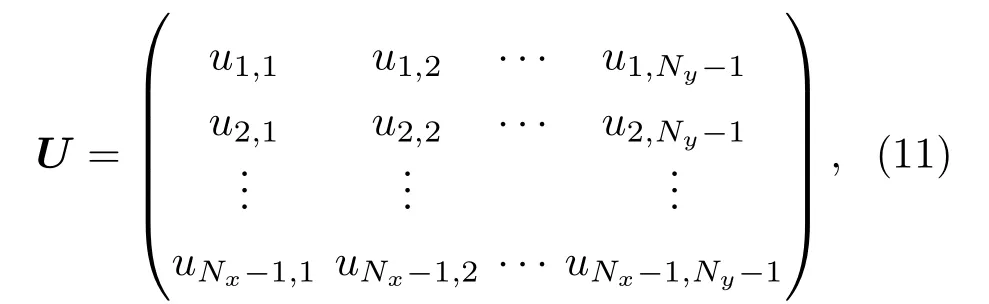
式中ui,j表示u在網格點(xi,xj)的數值解.引入Chebyshev一階微分矩陣和二階微分矩陣(具體推導過程見附錄B).則u(x,y)關于x的二階偏導數在配置點的值,可以用矩陣乘積的形式近似為矩陣Ax是在Chebyshev二階微分矩陣基礎上考慮Neumann邊界條件得到的,

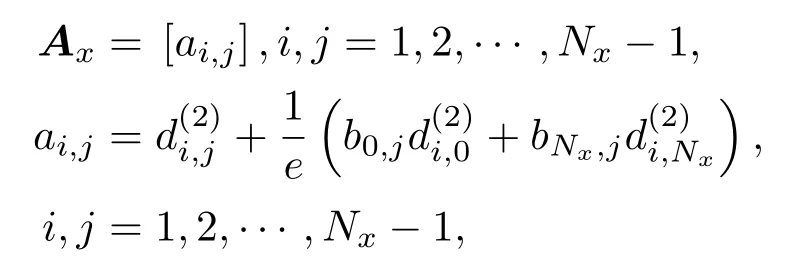
其中

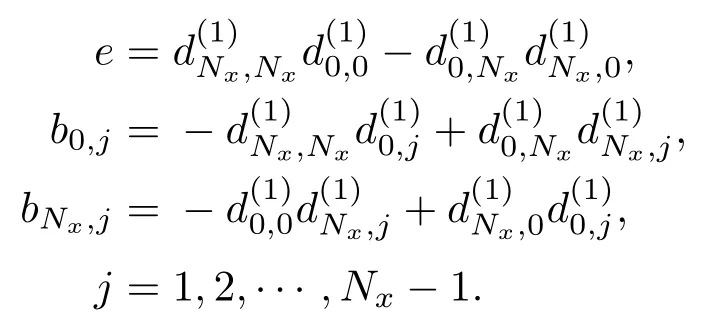
同樣地,對于y的二階偏導數,有UAy,其中矩陣Ay定義同Ax.借助譜微分矩陣,可將方程中的Laplace算子離散成矩陣乘積的形式,即將Chebyshev譜配置方法應用于反應擴散方程,得到其半離散形式為

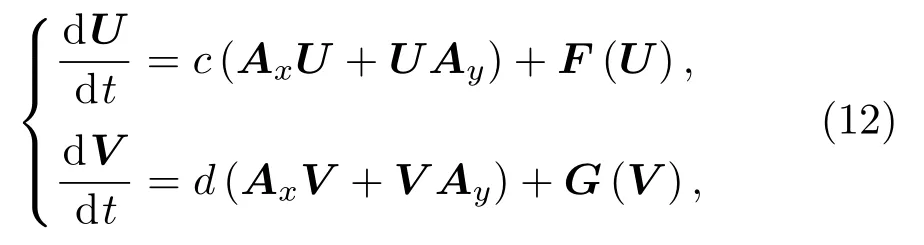
3.2 緊致隱積分因子法

將對空間離散后得到的非線性常微分方程組((12)式)采用緊致隱積分因子方法進行時間離散.定義時間步長為τ=Δt,第n層時間步為tn=nτ,n=0,1,2,···. 在(12)式兩端同時左乘指數矩陣e?Axt,右乘指數矩陣e?Ayt.為描述方便,取(10)式c=1,d=1,可將(12)式中第一個等式寫為

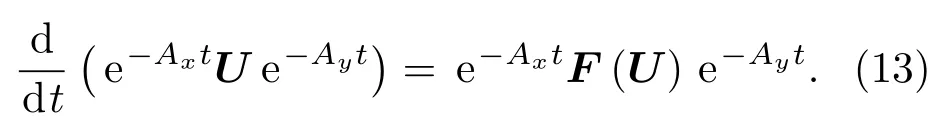
將時間離散為0=t0＜t1＜···,將(13)式在一個時間步長內關于時間積分,并用梯形公式近似可得二階緊致隱積分因子格式為

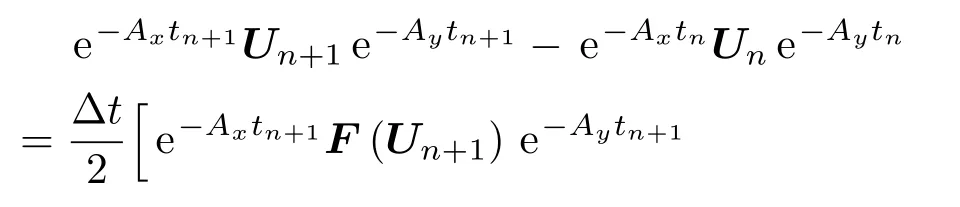
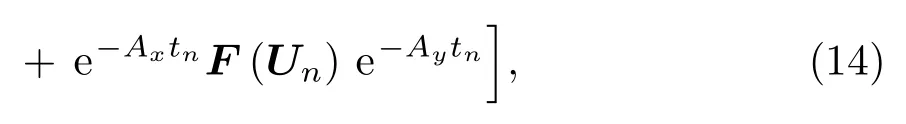
進一步化簡得

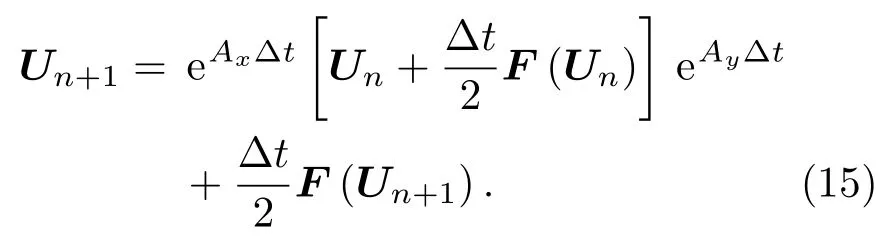
在非線性方程組(13)式中,右端第一項可以通過矩陣乘積得到,右端第二項采用Picard迭代方法求解:

同理處理(12)式中第二個等式可得

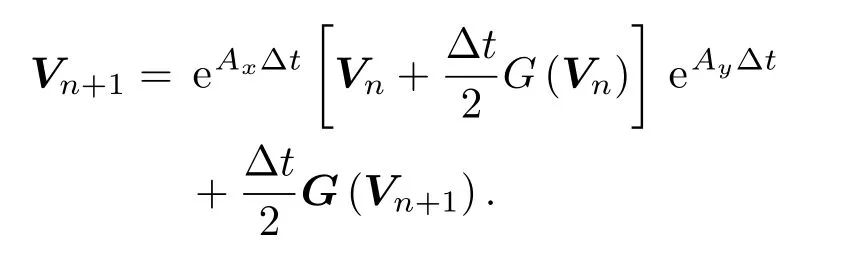
該方法中矩陣eAxΔt和eAyΔt的階數分別為Nx×Nx和Ny×Ny.在空間網格剖分量很大時,該方法可以降低存儲量和運算量,使計算速度更快.

4 數值算例

對于前述Gierer-Meinhardt模型,取?=(?1,1)×(?1,1),η=0.1,c=0.04,κ是不固定的參數.設

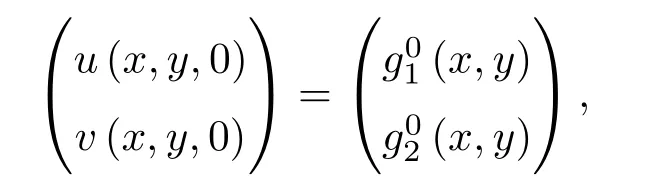
其中

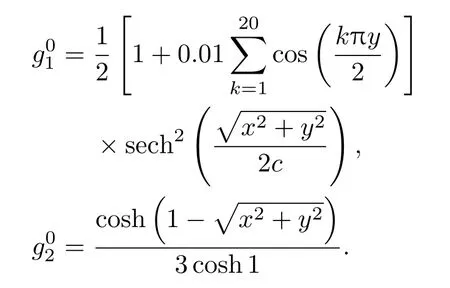
圖2 取κ=0.0128時Gierer-Meinhardt模型形成的斑圖 (a)t=20;(b)t=80;(c)t=170;(d)t=270;(e)t=320;(f)t=340;(g)t=500;(h)t=600;(i)t=900Fig.2.Turing patterns in Gierer-Meinhardt model when κ=0.0128:(a)t=20;(b)t=80;(c)t=170;(d)t=270;(e)t=320;(f)t=340;(g)t=500;(h)t=600;(i)t=900.

4.1 數值算例I

取κ=0.0128,N=100,h=2/100=0.02,τ=0.1h,t取圖2所示各值時,得到對應的圖像.由圖2可知,隨著時間的推移,初始擾動不斷增強擴大,最終形成清晰的斑圖.

4.2 數值算例II

取κ=0.0152,t取圖3所示各值,其他參數與算例I相同,可得到t取不同值時對應的圖像.由圖3可知,隨著時間的推移,初始擾動不斷增強擴大,最終形成清晰的斑圖.

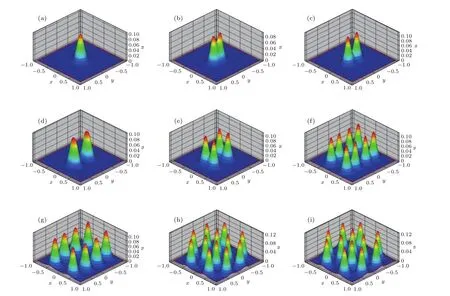
圖3 取κ=0.0152時Gierer-Meinhardt模型形成的斑圖 (a)t=30;(b)t=80;(c)t=90;(d)t=140;(e)t=160;(f)t=290;(g)t=520;(h)t=620;(i)t=990Fig.3.Turing patterns in Gierer-Meinhardt model when κ=0.0152:(a)t=30;(b)t=80;(c)t=90;(d)t=140;(e)t=160;(f)t=290;(g)t=520;(h)t=620;(i)t=990.

4.3 數值算例III

取κ=0.008,其他取值與算例II相同,t取不同值時對應的圖像如圖4所示.由圖4可知,隨著時間的推移,系統達到穩定狀態,反應擴散模型不能形成斑圖.

由數值模擬結果來看,其他條件一定的情況下,κ取不同值對于產生斑圖有重要的影響.數值模擬結果與理論結果一致.

此外,我們也對周期性邊界條件的Gierer-Meinhardt模型采用Fourier譜方法進行數值求解,結果顯示周期邊界條件對斑圖的形狀幾乎沒有影響.

5 結 論

介紹了圖靈斑圖形成的數學機理,并結合Gierer-Meinhardt模型,分析系統不穩定狀態的各系數需要滿足的條件,即產生斑圖的條件.運用緊致隱積分因子方法大大減少了存儲和CPU運算時間,該方法對于大時間數值模擬是一個高效、高精度的數值方法.數值算例模擬了斑圖形成的過程,驗證了理論分析結果.這些結論還可應用于求解帶有分數階的反應擴散方程組.

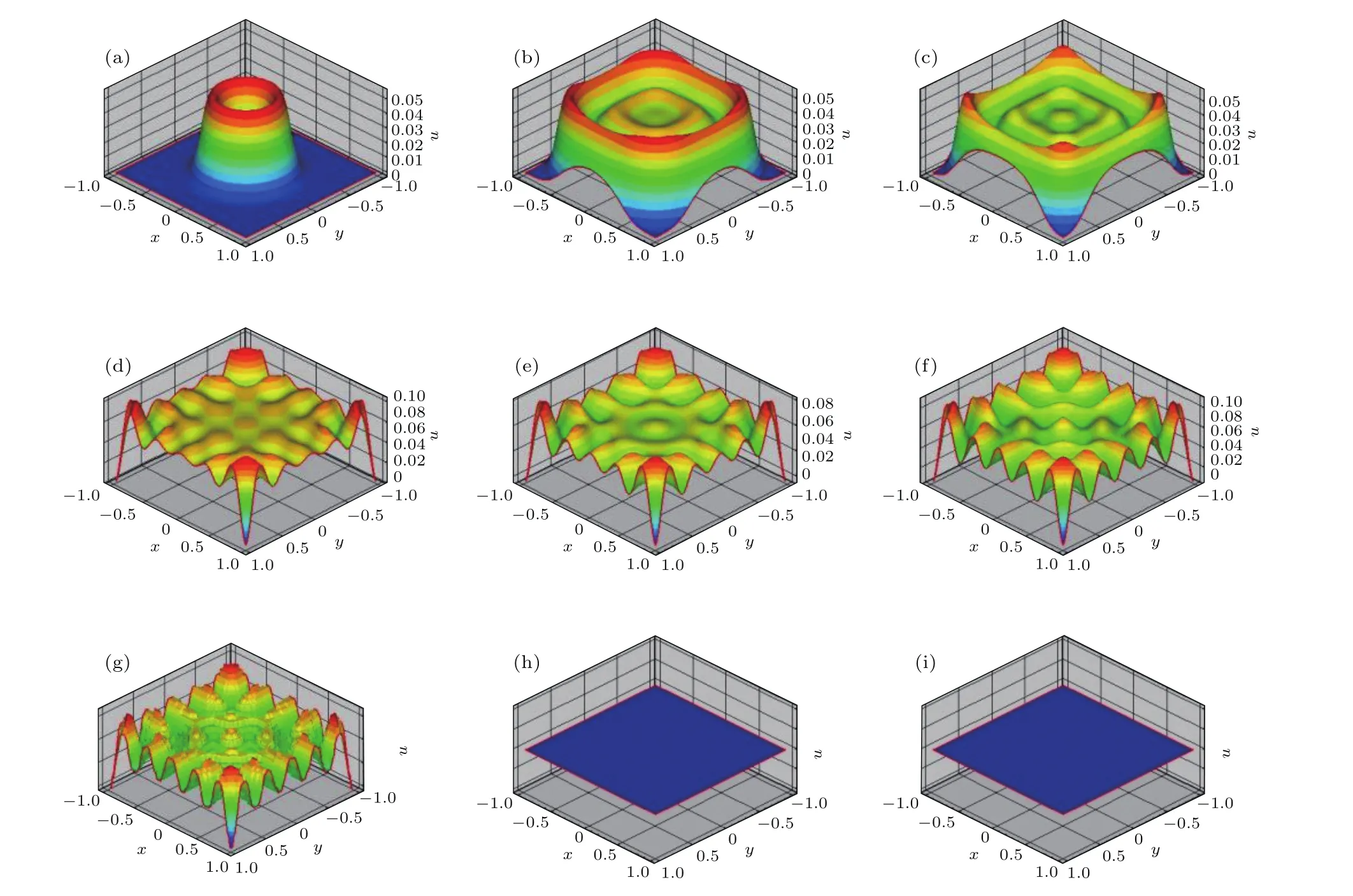
圖4 取κ=0.008時Gierer-Meinhardt模型形成的斑圖 (a)t=30;(b)t=80;(c)t=90;(d)t=140;(e)t=160;(f)t=220;(g)t=290;(h)t=270;(i)t=990Fig.4.Turing patterns in Gierer-Meinhardt model when κ=0.008:(a)t=30;(b)t=80;(c)t=90;(d)t=140;(e)t=160;(f)t=220;(g)t=290;(h)t=270;(i)t=990.

附錄A 圖靈斑圖的形成機理

首先在區域??RN(N=1,2)內考慮帶有齊次Neumann邊界條件的Laplace算子的特征值問題.一維情況下,特征值問題為

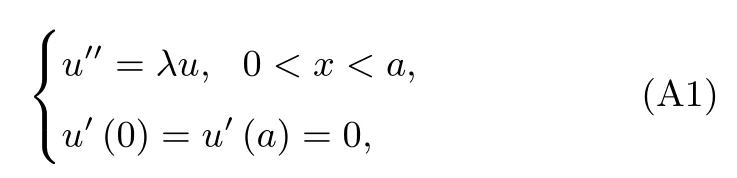
式中a∈R+.特征值問題可表示為μ2?λ=0,解得只有λ＜0時可解得特征值λk=?(kπ/a)2,且特征值所對應的特征函數為

在二維情況下,特征值問題為

式中a,b∈R+,應采用分離變量法求解特征值. 設u=X(x)Y(y),代入方程得設解得故特征值為λk,l=且特征值所對應的特征函數為

考慮方程組的特征值問題,令

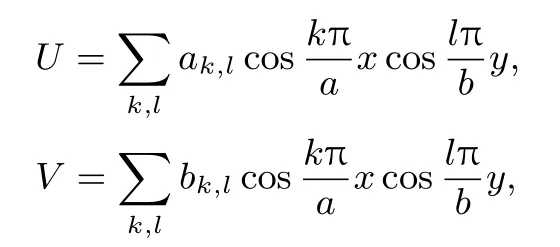
代入原方程組可得

當方程組(A3)有非零解,滿足

此時方程組所對應的特征值為

附錄B 譜微分矩陣

定義在[?1,1]上的標準k階Chebyshev多項式Tk(x)為Tk(x)=cos(karccosx),k=0,1,2,···. 令x=cosz,則有Tk=coskz,滿足如下遞推關系:

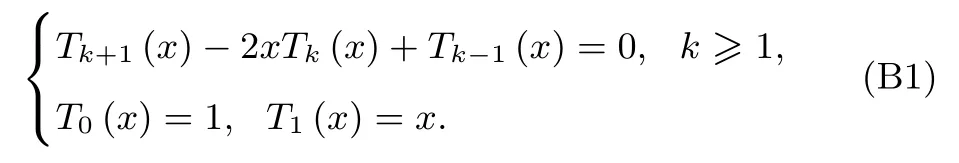
Tk(x)在[?1,1]上的N+1個Gauss-Lobatto點值為零:

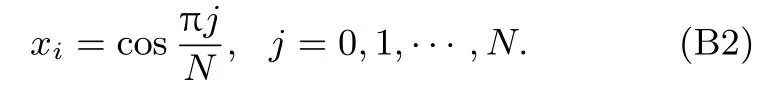
設N階多項式uN(x)∈PN在上述配置點xj滿足uN(xj)=u(xj),則有

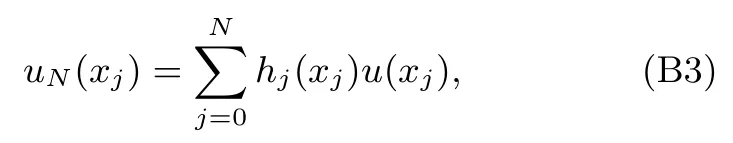
式中hj(x)為N階Lagrange基函數.用配置法求解未知量在網格點處的值,需要表示配置點處的導數值.對(B3)式求p階導數,得

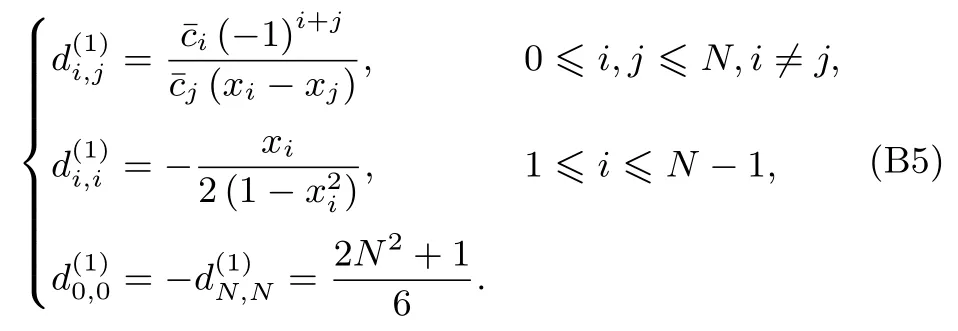
[1]Turing A M 1952Philos.Trans.R.Soc.Lond.B2 37

[2]Li X Z,Bai Z G,Li Y,Zhao K,He Y F 2013Acta Phys.Sin.62 220503(in Chinese)[李新政,白占國,李燕,趙昆,賀亞峰2013物理學報62 220503]

[3]Zhang L,Liu S Y 2007Appl.Math.Mec.28 1102(in Chinese)[張麗,劉三陽2007應用數學和力學28 1102]

[4]Li B,Wang M X 2008Appl.Math.Mec.29 749(in Chinese)[李波,王明新2008應用數學和力學29 749]

[5]Hu W Y,Shao Y Z 2014Acta Phys.Sin.63 238202(in Chinese)[胡文勇,邵元智 2014物理學報 63 238202]

[6]Peng R Wang M 2007Sci.China A50 377

[7]Copie F,Conforti M,Kudlinski A,Mussot A,Trillo S 2016Phys.Rev.Lett.116 143901

[8]Tompkins N,Li N,Girabawe C,Heymann M,Ermentrout G B,Epstein I R,Fraden S 2014Proc.Natl.Acad.Sci.USA111 4397

[9]Lacitignola D,Bozzini B,Frittelli M,Sgura I 2017Commun.Nonlinear Sci.Numer.Simul.48 484

[10]Gaskins D K,Pruc E E,Epstein I R,Dolnik M 2016Phys.Rev.Lett.117 056001

[11]Zhang R P,Yu X J,Zhu J,Loula A 2014Appl.Math.Model.38 1612

[12]Zhang R P,Zhu J,Loula A,Yu X J 2016J.Comput.Appl.Math.302 312

[13]Bai Z G,Dong L F,Li Y H,Fan W L 2011Acta Phys.Sin.60 118201(in Chinese)[白占國,董麗芳,李永輝,范偉麗2011物理學報60 118201]

[14]Zhang R,Zhu J,Yu X,Li M,Loula A F D 2017Appl.Math.Comput.310 194

[15]Lv Z Q,Zhang L M,Wang Y S 2014Chin.Phys.B23 120203

[16]Wang H 2010Comput.Phys.Commun.181 325

[17]Hoz F D L,Vadillo F 2013Commun.Comput.Phys.14 1001

[18]Nie Q,Zhang Y T,Zhao R 2006J.Comput.Phys.214 521

[19]Nie Q,Wan F Y M,Zhang Y T,Liu X F 2008J.Comput.Phys.227 5238

[20]Gierer A,Meinhardt H 1972Kybernetik12 30

[21]Ward M J,Wei J 2003J.Nonlinear Sci.13 209

[22]Wei J,Winter M 2004J.Math.Pures Appl.83 433

[23]Li H X 2015J.Northeast Normal University3 26(in Chinese)[李海俠2015東北師大學報3 26]