基于非線性預處理和神經網絡的字符序列單向Hash算法

朱 巍

(銳捷網絡股份有限公司，福建 福州 350002)

0 引言

單向Hash函數在數字簽名、身份認證、動態口令驗證和完整性校驗等領域中已經得到了相當廣泛的應用。傳統的單向Hash方法有MD5、SHA-1、RIPEMD-160和SHA-256等[1-2]，它們大多數基于復雜度的假設，需要進行大量的邏輯運算[3-4]，另外相關研究發現，這些算法已經并非足夠安全[5-7]。

基于神經網絡的Hash構造方法近些年來也引起了研究者的關注[8-12]。神經網絡由于其內部復雜性、混沌性、擴散特性以及狀態或者結構的時變性，已經被廣泛地應用于數據保護和加密算法中，并且隨著神經網絡的單向特性(例如假設神經網絡的輸出層維數小于隱含層維數，那么可以很容易地通過輸入得到輸出值，卻很難通過輸出值逆向推導出輸入)的不斷深入研究，在密碼學的單向Hash算法中，基于神經網絡的方法也越來越多被提出。

然而目前大量基于神經網絡的Hash方法并沒有針對身份認證這一越來越廣泛的使用場景進行優化，依然采用空白填充的方法將用戶的密碼序列進行對齊操作，這一步驟并不能增加信息的有效維度，并且加重了冗余計算，浪費了密碼空間的復雜度[13-15]。另外，很多Hash方法中將原始字符序列的ASCII碼直接輸入到神經網絡中，由于ASCII碼中存在很多‘0’的二進制位[16]，并不能充分利用神經網絡的輸入權值，并不利于最終Hash碼的魯棒性。

本文提出了一種基于非線性預處理和遞歸神經網絡(RNN)的字符序列的Hash構造方法，通過預先對字符序列進行非線性處理，得到字符序列的目標數值序列，并輸入到RNN中，經RNN計算后得到最終的Hash值。通過理論分析和實驗仿真，證明了本算法具有優秀的混沌擴散性質、抗碰撞能力以及單向特性，因此具有良好的理論研究價值以及現實應用意義。

1 Hash算法實現

1.1 非線性預處理

通過非線性預處理手段，可以將一維的字符序列映射到一個多維的混沌空間，有利于增強模型輸入的復雜性，從而獲得具有更加健壯的單向Hash函數構造模型。

設用戶的字符序列X=[x1，x2,…，xN]T，其中N為序列的長度，序列中每個字符xi(1≤i≤N)均使用統一的字符編碼集U進行二進制編碼，例如ASCII編碼、UTF-8編碼等等。

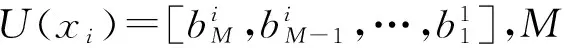
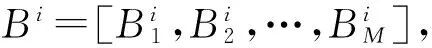
Ci=normalize(Di)

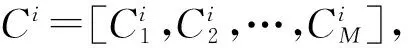
1.2 RNN的構建

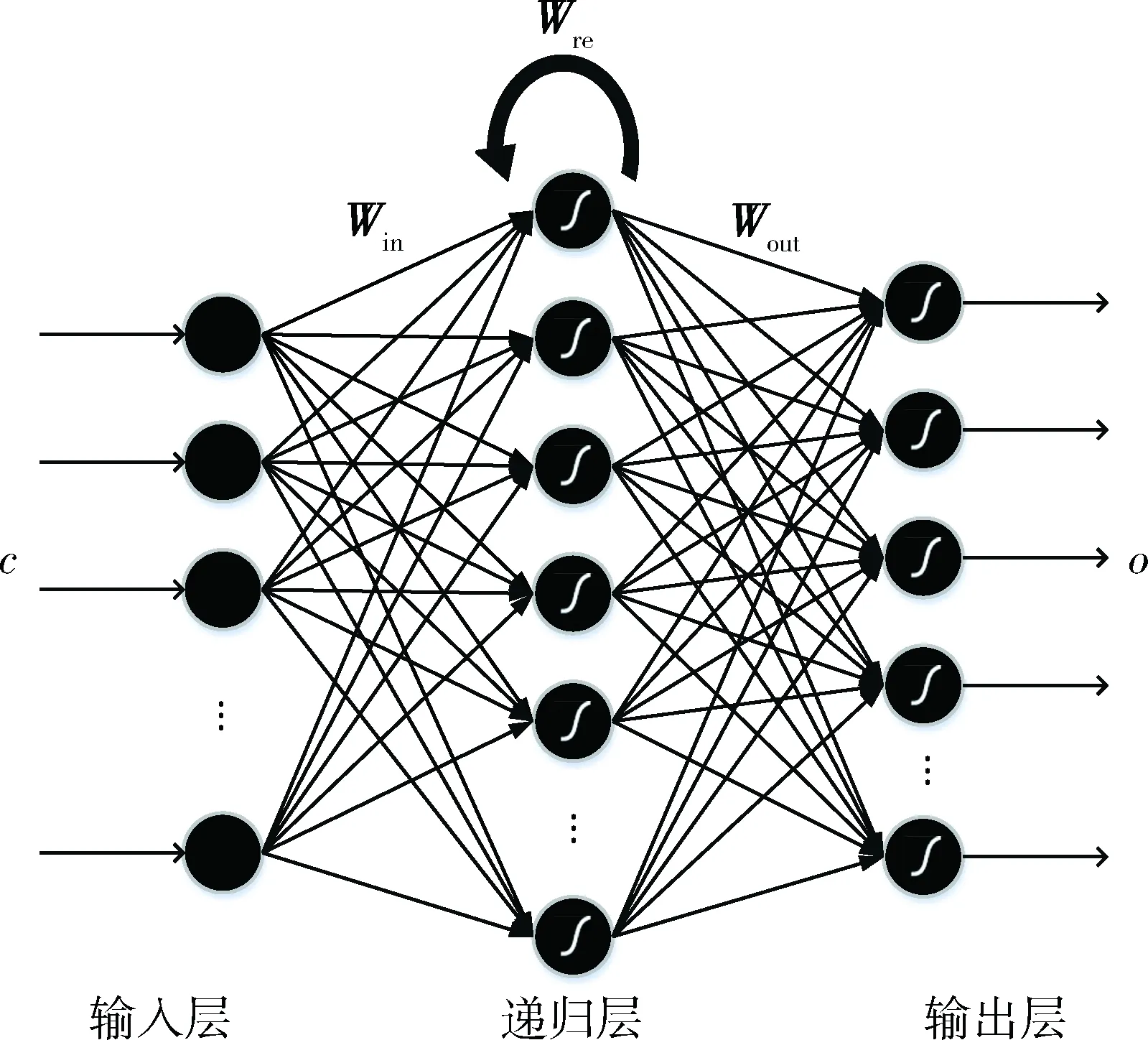
圖1 網絡模型

RNN結構如圖1所示。其中輸入層的節點數量為M(單個字符編碼長度)，輸出層的節點數量為期望得到的Hash碼的長度的1/k(k為預設的Hash碼增益長度系數)，記為L，中間遞歸層的節點數量記為P，且需要保證P>L。

對輸入權值矩陣Win∈P×M、遞歸層反饋權值矩陣Wre∈P×P以及輸出權值矩陣Wout∈L×P，遞歸層偏置值Bre∈P×1，輸出層偏置值Bout∈L×1分別進行隨機初始化。最后根據需要選定遞歸層和輸出層的激活函數，例如sigmod、tanh函數。

初始情況下，RNNN的隱含層神經元狀態為0，經過第一個輸入c1后，狀態為

S(1)=(Winc1+Bre)

(1)

從第二個輸入c2到最后一個輸入cN，隱含層神經元狀態為

S(i)=(Winci+WreS(i-1)+Bre)

(2)

最終網絡N的輸出為

O(N)=(WoutS(N)+Bout)

(3)

1.3 Hash過程

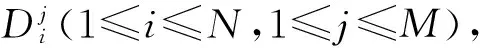
Hash的具體實施步驟如下：

(1)初始化遞RNN，包括RNN的結構規模、權值初始化以及隱含層神經元狀態置0。

(2)設置Hash碼增益長度系數k，最終得到的Hash碼長度將為k倍的RNN輸出層維數，即kL。

(3)對密碼字符序列進行非線性預處理，得到目標數值序列。

(4)將每個密碼子夫的目標數值序列依次輸入初始化好的RNN中，得到最終的網絡輸出O(N)。

(5)計算向量P=O(N)×10k，將P中每個元素值均轉換成十六進制值，并取后位串聯組成最終的Hash碼。

2 實驗

本文提出的算法采用MATLAB R2017a進行了實驗仿真，并且取得了較好的實驗效果，其相關代碼可以從GitHub下載：https://github.com/JuiLangCHU/NP_ANN_HashAlgorithm。

這里假設有密碼文本如下：

密碼1：1b2FC1Pe6B94aZbD4740D7kd9L9B844f9g

密碼2：2b2FC1Pe6B94aZbD4740D7kd9L9B844f9g

密碼3：1b2FC1Pe6B94aZbD4840D7kd9L9B844f9g

密碼4：1b2FC1Pe6B94aZbD4740D7kd9L9B844f9h

其中密碼2與密碼1僅首部第一個字符不同(1→2)，密碼3與密碼1僅中間第18個字符不同(7→8)，密碼4與密碼1僅尾部最后一個字符不同(g→h)。4組密碼的Hash值如圖2所示。

圖2 4組密碼序列的Hash值0、1序列圖形

2.1 單向性分析

對于神經網絡的最終輸出向量O，由于從小數點后第二位開始取若干位作為Hash碼，因此通過Hash值逆推網絡輸出的復雜度為o(24L)，L為神經網絡的輸出層維度，可見當網絡輸出層維數較大時，此步驟的計算復雜度相當高。

圖4 改變密碼序列不同位置的一個字符時，Hash碼發生改變的比特數量(總Hash碼長度為128)

另外，根據神經網絡最終輸出公式(3)得:

WoutS(N)=f-1(O)-Bout

(4)

其中，Wout∈L×P，S∈P×1，令φ=f-1(O)-Bout∈L×1，對公式(4)展開，可以得到：

?

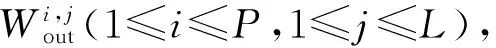
2.2 碰撞性分析

抗碰撞是指對于兩個不同的原始輸入序列，經過Hash算法后得到的Hash值相同的概率非常小。實驗中，對于1個密碼序列任意改變其中某一位置的一個字符，經過本算法得到128 bit的Hash碼，并統計相同位置上對應的Hash值相同的次數，經仿真，統計結果分布如圖3所示，超過18個字符相等的Hash碼出現概率為0，說明算法具有良好的抗碰撞能力。

圖3 相同位置具有相同Hash值的統計次數

2.3 擴散性和均衡性分析

隨機取一段密碼序列，并分別更改密碼序列的首部、中部、尾部以及隨機位置的一個字符，然后計算原始密碼以及字符發生變化之后的Hash值，實驗中Hash碼的長度為128 bit。通過1 000次測試，計算得Hash碼發生變化的比特數量分別為64.194、64.111、63.899、64.161，如圖4所示。

由此可見，即使是不同位置的密碼字符出現變化，對最終的Hash碼的影響幾乎是相同的，說明該Hash算法的平衡性非常均勻，并且最終Hash碼的比特變化數量均非常接近Hash碼總長度的50%，即64 bit，也說明了該Hash算法的混亂擴散性比較出色，能夠敏銳地感知到原始密文序列出現的微小差異。

2.4 信息熵測試

為了度量一段消息中所含的信息容量，1948年由SHANNON C E提出了信息熵的概念，在信息論中，當熵最大時，信息量最大。對于Hash函數而言，熵最大時，Hash值的分布也越混亂，信息復雜度越高。熵的數學度量模型為：

且滿足

0≤H(X)≤log|X|

其中|X|為取值個數。僅當變量X符合均勻分布時，H(X)=log|X|，即此時H(X)為最大熵。

為此，計算序列Hash碼的信息熵，X為Hash碼中不同字符的集合。

由于這里Hash碼的取值為十六進制的0至F，理論上的熵最大值為log216=4 bit。對比以上4組密碼序列的熵值(如表1所示)，可見已比較接近最大熵，表明其Hash碼的混亂程度也趨近最大。

表格1 不同密碼序列的信息熵值

3 結論

本文提出了一種基于非線性預處理和RNN相結合的密碼文本序列Hash算法，其中非線性預處理可以顯著地擴大遞歸神經網絡輸入層中不同字符的輸入差異性，從而實現Hash構造函數對于微小差異的序列具有高敏感性。結合RNN中的參數敏感性、非線性等特點，可以實現安全地抗攻擊的Hash構造方法，相關實驗分析也證明了其有效性。此外由于RNN中的參數取值靈活，網絡的規模也可以根據實際需要進行調整，因此在Hash實現中不需要對網絡進行訓練。綜上所述，本文提出的算法具有高靈活性、易用性、擴展性和用戶自定義配置性。

[1] RONALD L. RIVEST. The MD5 message-digest algorithm [R].MIT Laboratory for Computer Science and RSA Data Security, 1992.

[2] Federal information processing standards publication 180-1. secure hash standard [S]. 1995.

[3] Wang Shihong, Hu Gang. Coupled map lattice based hash function with collision resistance in single-iteration computation [J]. Information Sciences. 2012 Jul 15;195:266-76.

[4] WANG SHIHONG, LI DA, ZHOU HU. Collision analysis of a chaos-based hash function with both modification detection and localization capability [J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 195(13):166-276.

[5] Wang Xiaoyun, Yao Fang. Crypt analysis of SHA-1 hash function [C].Proceedings of the 25th International Cryptology Conference, 2005:19-35.

[6] Xiao Di, Liao Xiaofeng, Wang Yong. Improcing the security of a parallel keyed hash function based on chaos map [J]. Physics Letter A, 2009:4346-4353.

[7] Yang Gang, Yi Junyan. Dynamics characteristic of a multiple chaotic neural network and its application[J]. Soft Computing, 2013:783-792.

[8] ABDOUN N, ASSAD S E, TAHA M A, et al. Secure Hash Algorithm based on Efficient Chaotic Neural Network [C]. 2016 International Conference on Communications. IEEE, 2016: 405-410.

[10] 陳軍, 韋鵬程, 張偉, 等. 基于RBF神經網絡和混沌映射的Hash函數構造 [J]. 計算機科學, 2006, 33(8):198-201.

[11] 李國剛, 鐘超林, 藺小梅. OHNN新的分組Hash算法 [J]. 華僑大學學報(自然科學版), 2015,36(4):393-398.

[12] XIAO D, LIAO X, WANG Y. Parallel keyed hash function construction based on chaotic neural network [J]. Neurocomputing, 2009, 72(10):2288-2296.

[13] LIAN S, SUN J, WANG Z. Secure hash function based on neural network [J]. Neurocomputing, 2006,69(16):2346-2350.

[14] HE B, LEI P, PU Q, et al. A method for designing hash function based on chaotic neural network [C]. International Workshop on Cloud Computing and Information Security (CCIS), 2013.

[15] LIAN S, LIU Z, REN Z, et al. Hash function based on chaotic neural networks [C]. Circuits and Systems, 2006.ISCAS 2006.IEEE, 2006: 4.

[16] URBANOVICH P, PLONKOWSKI M, CHURIKOV K. The appearance of conflict when using the chaos function for calculating the hash code [J]. Network, 2012, 88(11b): 346-347.