基于優化參數的LS-SVM模型的股票價格時間序列預測

闞子良，蔡志丹

（長春理工大學 理學院，長春 130022）

股票預測涉及到投資者的經濟利益，如何能提供較準確的股票預測一直是人們關注的熱點問題。根據國內外專家學者的研究，當代金融數據越來越呈現出非線性的特征，傳統時間序列的預測方法，比如AR、MA和ARMA等基于線性數據的模型，早已經不能適應需要。而神經網絡[1］方法雖能提供較精確的結果，但是有網絡模型和結構選擇困難的缺點，容易陷入局部最小，訓練速度慢，泛化能力差等現象。近年來支持向量機技術是神經網絡之后出現的一種解決非線性問題的有效方法，屬于機器學習[2-3］范疇，可以克服傳統統計方法[4］和神經網絡的很多缺點。

具體實驗時，先運用最小二乘法改進運算效率和預測精度，考慮到支持向量機技術對參數的敏感性，又采用遺傳算法優化支持向量機[5-10］的兩個參數Gamma和γ。將某公司的107天的股票價格數據進行預測（含今日開盤價，收盤價，最高價，最低價，交易量，10日移動平均線，30日移動平均線和RSI）。將次日的收盤價為輸出，利用主成分分析法提取20個變量中累積貢獻率大于95%的變量為輸入，訓練模型并得出測試數據的預測值，對比模型參數優化前后的預測效果，從而對該改進算法進行分析。

1 股價預測模型的原理

1.1 傳統支持向量機的基本原理

支持向量機是針對解決兩種類別的分類問題而提出的。第一種是線性可分問題。設訓練數據：x1，x2，...，xn，x∈Rn。

分類超平面最常見的表達式如下：

將訓練數據和標簽集轉換為這樣的形式：(x1，y1)，...，(xn，yn)，x∈Rn，y∈{+1，-1} 。于是激活（傳遞）函數可定義為：

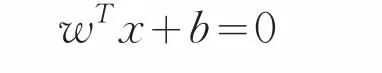
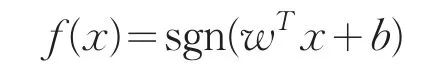
sgn表示符號函數，對應分類標簽，函數只有兩個輸出值-1和+1。wTx+b=0是要尋找的最大間隔超平面。

訓練樣本為線性不可分時，加入正松弛變量ξi，i=1，2，...，n和懲罰因子C，原始問題為：

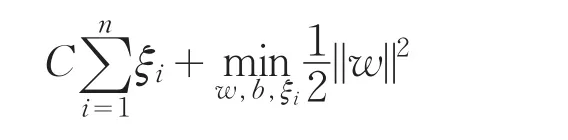
經過同樣的推導過程，對偶優化問題為：

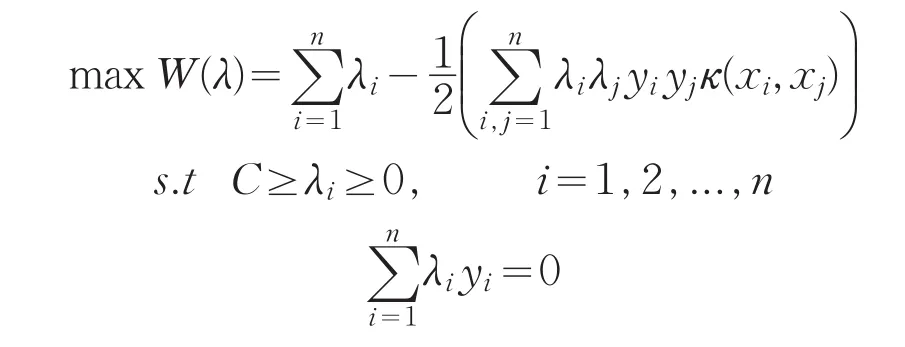
1.2 基于PCA-GA方法的參數尋優過程[11-12］

由于采集得到的股票數據的維數有20個，維數過大，故采取基于PCA去噪的參數尋優最小二乘支持向量機，主成分分析（PCA方法）是1901年由皮爾遜引入，1933年霍特林發展了該理論。主成分分析的就是將具有一定相關性的多個變量，組合成為一組相互無關的綜合變量，進而代替原變量。具體預測步驟如下：

（1）下載樣本數據集，歸一化處理初始數據集。

（2）應用主成分分析法，提取累積貢獻率達到90%以上的主成分作為輸入變量。

（3）選取訓練樣本和測試樣本。

（4）不通過參數的尋優對樣本進行訓練。再通過GA優化訓練樣本的參數，并進行回歸訓練。

（5）將測試樣本輸入訓練好的LS-SVM和SVM回歸模型中，輸出預測結果，計算預測精度和擬合優度，比較優化前后的預測效果。

2 股票價格的預測及結果分析

2.1 樣本的選取和預處理

由于最小二乘支持向量機的訓練需要樣本量足夠大才能保證預測精度達到一定水平，在統計軟件上提取了某公司的107天的股票價格，行變量為日期，列變量為今日的開盤價，收盤價，最高價，最低價，交易量，10日移動平均線，30日移動平均線和RSI。每列歸一化后，將第二日的收盤價作為輸出，用主成分分析法提取20個變量，累積貢獻率95%以上的變量作為輸入變量。考慮到訓練樣本應多于測試樣本，前100天的數據應為訓練樣本，剩下的7天為測試樣本。

2.2 對比方式

為了清晰地展現出優化前后的模型的效果差異，通過分析模型在計算機運行的時間長短，模型的均方誤差，相關系數，畫出期望輸出和預測輸出圖，以及誤差圖，驗證遺傳算法優化最小二乘支持向量機參數可以極大提高模型的預測精度。

利用所建立的模型對股票數據預測后，為了解預測效果的好壞，即對預測的結果進行檢驗。現采用計算實際值與預測值的均方誤差MSE來評價模型的好壞。MSE越小，說明預測精度越高，模型越好，反之，則越差。比較幾種模型對相空間重構后的兩組數據預測的MSE，分析對比出模型間的差異，以及優化的效果。

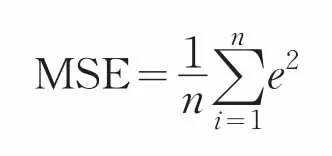
其中，e為實際值與預測值的差。

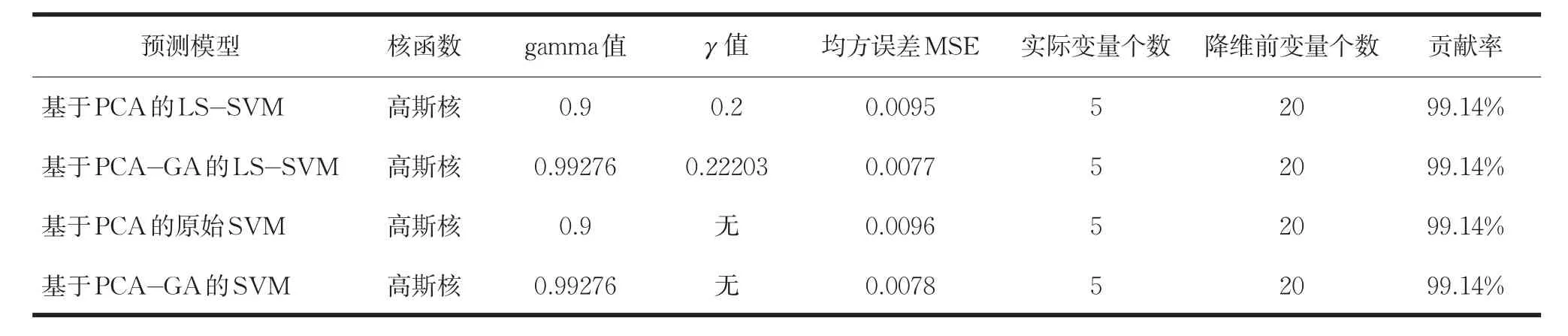
表1 各模型的參數與預測效果

2.3 實證研究過程

（1）預處理從同花順股票軟件下載的數據后，建立4個模型預測股票價格的開盤價，分別是原始的PCA-LS-SVM和基于GA算法、PCA的LS-SVM以及基于PCA的原始SVM和基于PCA-GA的SVM。從這四個模型看遺傳算法是否能提高LS-SVM和SVM的預測效果。

（2）在Matlab中采用PCA提取累積貢獻率大于95%的變量，利用計算機對變量進行主成分分析之后，得到最好的5個主成分，第一個主成分的貢獻率約為65.93%，而這5個主成分的累積貢獻率為99.14%。其次，建立原始的PCA最小二乘支持向量機模型。然后，通過實驗實現基于GA算法、PCA的最小二乘支持向量機的預測過程，根據第1步的結果，利用遺傳算法訓練具有5個變量的新訓練樣本，得出其優化的參數g和γ。接著，將這兩個參數代入到樣本的訓練之中，利用訓練好的模型進行預測。SVM模型按同樣的步驟進行。

（3）比較這兩個模型的預測效果。運用MSE指標判斷預測好壞，依據實驗過程，總結出表1。

2.4 實證結果分析

可以從表1看出，經過遺傳算法的參數優化后，無論原始的支持向量機，還是最小二乘支持向量機，其預測的均方誤差都極大降低了，這證明了遺傳算法的有效性和適用性；另外，4個模型中，均方誤差最小的是基于PCA-GA的LS-SVM模型，其次是基于PCA-GA的SVM模型，說明了LS-SVM比SVM效果更好；鑒于高斯核比其他核函數具有更大的優勢，實驗均采用高斯核作為核函數。

現利用軟件得出基于PCA-GA的最小二乘支持向量機模型在測試樣本中的預測結果，如圖1所示；預測結果圖有上下兩條線，上面的線是實際值，下面的線是預測值。可以看出，這兩條線的走勢基本一致，誤差大小在2.5以內。

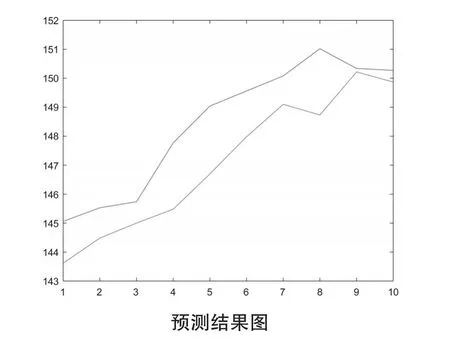
圖1 基于PCA-GA的LS-SVM預測圖

3 研究結論

通過利用多種模型對股票的收盤價進行預測實驗，從實驗的解決問題的過程和預測結果中，總結出如下的結論：

支持向量機模型可以僅僅利用很少的數據就能得出比較精準的預測結果。而且訓練樣本最好取距離測試樣本較近的數據。

訓練樣本取太多，會導致模型泛化能力差，在訓練樣本內誤差小，但在測試樣本內會誤差較大。

遺傳算法對最小二乘支持向量機的參數的優化能極大提高建模的速率，還能使預測精度大大提升。這說明組合預測方法較單一的預測更有效。

機器學習作為股票等金融數據預測的有效方法，一方面大幅度地提升了分析處理這類數據的能力，另一方面還降低了成本。這種方法同樣適用于其他復雜類型數據的預測。

[1]宋玉強.人工神經網絡在時間序列預測中的應用研究[D］.西安：西安建筑科技大學，2005.

[2]孫翔侃，白寶興.基于機器學習的NAO機器人檢測跟蹤[J］.長春理工大學學報：自然科學版，2016，39（2）：116-119.

[3]朱成璋.基于機器學習的時間序列預測關鍵技術研究[D］.長沙：國防科學技術大學，2014.

[4]Xiao QK，Xing L，Song G.Time series prediction using optimal theorem and dynamic Bayesian network[J］.Optik-International Journal for Light and Electron Optics，2016，127（23）：11063-11069.

[5]梅倩.LS-SVM在時間序列預測中的理論與應用研究[D］.重慶：重慶大學，2013.

[6]王鵬，高鋮，楊華民.基于邊分類的SVM模型在社區發現中的研究[J］.長春理工大學學報：自然科學版，2015，38（5）：127-130.

[7]梁禮明，鐘震，陳召陽.支持向量機核函數選擇研究與仿真[J］.計算機工程與科學，2015，37（6）：1135-1141.

[8]郭小溪，李剛，閆偉杰.基于遺傳算法整定PID的自主潛器深度控制[J］.長春理工大學學報：自然科學版，2010，33（3）：37-39.

[9]陳偉根，滕黎，劉軍，等.基于遺傳優化支持向量機的變壓器繞組熱點溫度預測模型[J］.電工技術學報，2014，29（1）：44-51.

[10]韓敏，許美玲，穆大蕓.無核相關向量機在時間序列預測中的應用[J］.計算機學報，2014，37（12）：2427-2432.

[11]邵小健.支持向量機中若干優化算法研究[D］.青島：山東科技大學，2005.

[12]畢建新，張志春，李小波.基于遺傳算法的航空裝備預防性維修優化研究[J］.長春理工大學學報：自然科學版，2011，34（03）：62-65.