人類第一次測量地球

文｜梁衡

公元前305年，有兩個人平躺在亞歷山大港外沙灘上。一個是阿基米德（公元前287～前212年），另一個是他的朋友，地理學家埃拉托色尼（公元前275～前195）。突然，阿基米德一骨碌翻身爬起，手里捏著一把沙子道：

“埃拉托色尼，你說這一把沙子有多少粒？”

“大概有幾千、一萬粒吧。”

“這一片海灘的沙子有多少粒？”

“這可說不清！”

阿基米德跳起來，雙手捧起一捧沙子向天空揚去：“假如我把沙子撒開去，讓它塞滿宇宙，把地球、月亮、太陽和金、木、水、火、土等行星統統都埋起來，一共要多少粒？”

“啊？——”埃拉托色尼也一骨碌爬起來，驚得說不出話來，半天才回答道：“不可能，不可能！親愛的阿基米德，你怕不是瘋了吧，要知道你是永遠算不出來的！”

“我就要算一個給你看看。”

“我不信。”

“好，三天后我們再在這里見面。”阿基米德說完后，兩人揮手而別。

埃拉托色尼的擔心不是沒有道理的。當時世界上還沒有發明方便的阿拉伯數字。希臘人用他們的27個字母分成三組，分別代表個、十、百、千位數，到一萬就是最大的了，再大就無法表示和計算了。

可是，阿基米德立即找來一粒球形的橄欖核，算出它的體積等于幾粒沙子，又依次推算地球的體積、宇宙的體積等于多少枚橄欖核。當數字超過一萬時，他聰明地把萬作為一個新起點，叫它第一階單位，然后再往上數到萬萬，叫第二階單位，這樣就可以依次推到很大很大。過了些日子他已經算出這個龐大的數字：塞滿宇宙需要一千萬個一千萬的第八階單位粒沙子，用今天的數學方式來表示可以寫成：107(1000萬)×107×8(第八階)，再確切一點就是1后面寫上63個零。

當然，這個數字在今天看來是不能成立的，因為宇宙是沒有邊緣的。阿基米德是根據當時人們認為的宇宙半徑來算的。可是這樣一算，他倒是找到了一種數學新概念：“階”。“階”相當于后來數學上的“冪”。

第三天中午剛過，阿基米德便如約向沙灘走去。當他來到沙灘時，埃拉托色尼比他來的還早，正面對大海，右手還拄著一根高高的細竹竿，既不像釣魚，也不像撐船。阿基米德悄悄走到他背后大喊一聲：“我來了！”

埃拉托色尼一見是他，忙笑著說：“啊，原來是你。是來認輸的吧。”

“科學無戲言，阿基米德什么時候說過假話？”接著阿基米德便將他算的結果如此這般地說了一遍。 說完又得意洋洋地抓起兩把沙子拋向天空：“世界在我的手中！”

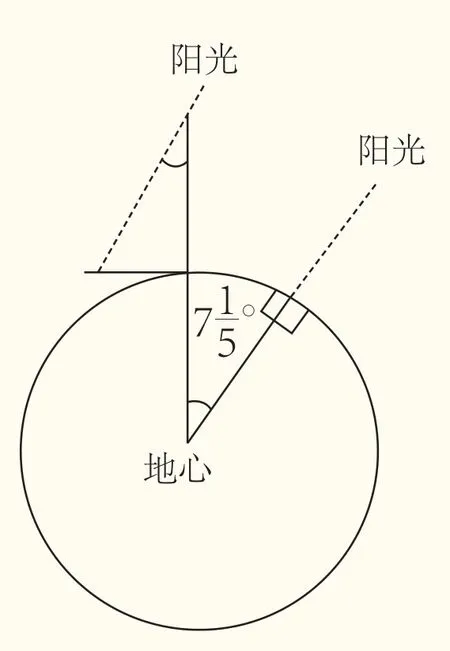
埃拉托尼測地試驗

不料埃拉托色尼并不以為然，他將竹竿往沙地上一插說：“你能知道宇宙裝得下多少沙子，可是你知道地球周長有多少？”

這一問倒把阿基米德問住了，他沒想到這個比他小十二歲的朋友這樣年輕氣盛。 今天是專和他斗法來的，便反過來將他一軍：“難道你知道有多長？”

“不瞞你說，在你數沙子的時候我已經測好了。”

“啊！”阿基米德覺得新鮮極了，“你用什么辦法測得？”

“這很簡單，我只用了一根三尺長的竹竿。”

“難道你用竹竿把地球量了一圈？”

“不！我就站在這里不動！”埃拉托色尼認真地講述起來，“你知道，離亞里山大里亞5000斯塔迪姆（埃及長度計算單位）有一個城市叫塞恩，夏至那天，陽光可以直射到井底，說明光線與塞恩城的地面垂直，而在我們亞里山大里亞的物體卻有一個短短的影子。我就拿這一根竹竿在亞里山大里亞廣場上這么一立，就能算出這兩個城市與地球球心形成的夾角，再一量這兩個城市間的距離……”

“就能推出地球的周長。妙！妙！”整天研究三角、圓弧的阿基米德心有靈犀，一點就通。他不等埃拉托色尼說完就著急地問：“夾角多大？”

“7°。”

“距離多少？”

“5000斯塔迪姆。”

“啊，地球周長25萬斯塔迪姆。”阿基米德說的這個數字合4萬公里，與我們近代測得數字僅差100公里。

“阿基米德，你這個數學腦袋可真厲害啊！”