基于TW-TOF的UWB室內定位技術與優化算法研究

牛群峰，曹一帆，王 莉，惠延波

（河南工業大學 電氣工程學院，鄭州 450000）

基于UWB的定位技術有著精度高、功耗低、抗干擾能力強等優點，非常適合室內定位領域[1]。在導航制導以及目標定位跟蹤領域，卡爾曼濾波作為最佳的線性濾波器被廣泛使用[2]。本文使用DWM1000信號收發模塊，采用基于雙向飛行時間的測距方法并使用三邊定位法構建UWB定位系統實現對室內移動人員的實時定位。對帶有噪聲干擾的定位數據使用IMM卡爾曼濾波對定位數據進行處理，并對處理結果進行分析。

1 UWB定位原理

UWB定位是基于測量距離的定位技術，其定位方法有TDOA、三邊定位法等，測距的方法也是多種多樣的[3]。本文采用的是基于飛行時間的雙向測距方法TW-TOF測距，然后使用三邊定位法計算坐標。

1.1 TW-TOF

基于飛行時間的雙向測距方法TW-TOF是一種不需要通信雙方時間同步的測距方法，避免了為獲得時間同步增添的額外成本。這種測距方法要求基站和標簽都具有信號收發功能，標簽周期性的初始化距離測量信息，基站實時接收回復標簽信號，并測量距離。具體步驟如圖1所示。

圖1 基于飛行時間的雙向測距步驟Fig.1 Steps based on TW-TOF

當基站收到標簽的輪詢信息，基站記錄此時的時間TRP，并發送回復信息給標簽，并記錄發送時間TSR。當標簽收到回復信息后，記錄接收時間TRR，并在 TSF時將標簽記錄的時間（TSP、TRR、TSF）發送給基站。基站獲得標簽發送的最終信息后獲得足夠的數據計算距離并進行以下計算：

（1）標簽的信號往返延遲時間 TTRT=（TRR-TSP）減去這期間基站的反應時間得到 2次標簽到基站的單程飛行時間tTA、tAT。

（2）基站的信號往返延遲時間 TART=（TRF-TSR）減去這期間標簽的反應時間同理得到2次標簽到基站的單程飛行時間。

之后，基站將上邊求得的標簽到基站的飛行時間求和并取平均值，得到單程飛行時間TOF。這樣

TRSP跟不相同時，采用不對稱雙向測距以獲得TOF計算結果：

TOF乘以光速（UWB信號傳遞速度）便得到標簽到基站的距離。

1.2 三邊定位法

在通過TW-TOF等方法測得至少3個標簽到基站的距離，在上位機或是基站使用三邊定位法對標簽的位置進行計算便可得到目標的位置坐標，如圖2所示。

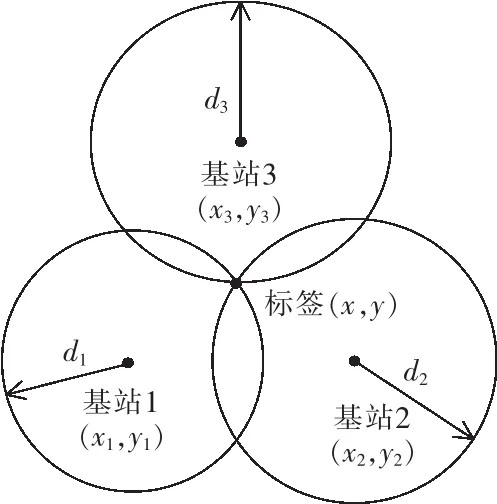
圖2 三邊定位法原理Fig.2 Principle of three sides location method

可以計算出唯一的交點作為標簽點的位置。使用式（3）～式（6），根據測得的標簽到基站的距離 di，可得到標簽的位置（x，y）。

式（5）和式（6）中 di（i=1，2，3）為標簽分別到 3個基站的距離。

2 卡爾曼濾波

通過TW-TOF測距可以算出標簽到各個基站的距離，進而得到目標的位置。但在實際測量過程中由于非視距，多徑傳播以及人體等造成的隨機干擾，導致觀測到的信息中往往夾雜有隨機噪聲，造成觀測到的定位的結果存在誤差。卡爾曼濾波是最佳線性濾波器，實現簡單，是純時域的濾波器，被廣泛使用在導航制導、目標定位和跟蹤等工程領域[3]，并且其計算復雜度低，非常適合移動設備。使用卡爾曼濾波，利用上一時刻位置信息和本時刻的觀測值對本時刻位置進行最優估計，被估計量隨時間變化，這是一種動態估計。在目標跟蹤中，不必知道目標的運動模型就能夠實時地修正目標的狀態參數如位置、速度等。

2.1 傳統離散卡爾曼濾波器原理

用卡爾曼濾波獲得最優估計值分為2個階段。第一階段使用上一時刻的信息對當前時刻的位置進行預測估計；第二個階段，使用當前時刻的帶有噪聲的觀測值對估計值進行修正。傳統離散卡爾曼濾波器由以下5個公式組成。

式（7）為狀態預測方程，對當前狀態進行預測。式中矩陣At為狀態轉移矩陣，表示在沒有噪聲和控制量時2個連續時刻狀態的關系；為當前狀態的估計值；ut為t時刻的控制量，如在定位系統中為動力系統的加速度控制信號；矩陣Bt為控制矩陣，描述控制量如何作用于當前狀態。式（8）為預測估計誤差的協方差方程。式中Pt

式（9）、式（10）為狀態更新方程和最優增益矩陣方程。式中為最優估計值；Kt為最優增益；為實際觀測值與預期觀測值的殘差；H為觀測矩陣。

卡爾曼濾波器最后一個方程為濾波誤差協方差更新方程：

2.2 交互多模型卡爾曼濾波原理

試驗中發現，傳統卡爾曼濾波能有效降低做勻速直線運動定位目標的噪聲干擾，得到理想的濾波效果。但當定位目標進行直角轉彎或加減速這些室內常見動作時，僅采用基本的卡爾曼濾波會出現“滯后”等現象，短時間內造成較大的誤差。這時需要自適應算法。交互多模型算法IMM使用2個或更多的模型來描述工作過程中可能的狀態，最后通過有效的加權融合進行系統狀態估計，很好地克服了單模型估計誤差較大的問題。

IMM算法結構由5部分組成，如圖3所示，包括計算模型混合概率、輸入交互、對各模型進行卡爾曼濾波、模型概率更新以及輸出交互[4]。

圖3 IMM算法步驟Fig.3 Steps of IMM algorithm

2.2.1 計算模型混合概率

假定目標有r種運動狀態，對應有r種狀態轉移方程。各模型之間的轉移由馬爾可夫概率轉移矩陣確定，其中元素pij表示目標由第i個運動模型轉移到第j個運動模型的概率，概率轉移矩陣如下：

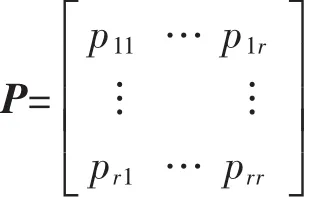
模型i到模型j的混合概率為

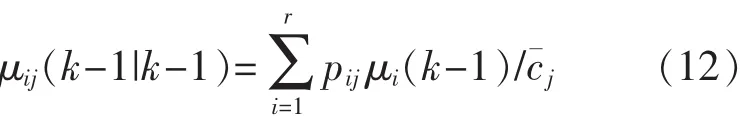
式中：μi（k-1）為上一時刻每個濾波器的模型概率；j為模型 j的預測概率（歸一化常數），如式（13）所示：

2.2.2 輸入交互

在這一部分，要重新初始化濾波輸入，由上一時刻各模型估計與混合概率得到混合狀態估計0j（k-1|k-1）和混合協方差估計 P0j（k-1|k-1），將混合估計作為當前循環的初始。對模型j，混合狀態估計混合協方差估計方程可分別由式（14）～式（16）得到。式中：i（k-1|k-1），Pi（k-1|k-1）為上一時刻的狀態估計與協方差估計。

2.2.3 各模型卡爾曼濾波

這一部分，對不同的運動模型選擇合適的卡爾曼濾波器進行濾波。

2.2.4 模型概率更新

模型概率計算是假設檢驗過程，即采用貝葉斯假設檢驗方法檢驗濾波器組各個濾波器的殘差[5]。采用似然函數來更新模型概率μj（k），模型j的似然函數為

式中：vj（k）為濾波殘差，如式（18）所示，Sj（k）可由式（19）得到：

模型j的概率為

式中：c為歸一化常數，如式（21）所示：

2.2.5 輸出交互

由第四步獲得更新的模型概率后，輸出交互，對每個濾波器的估計結果加權合并，得到總的狀態估計（k|k）和總的協方差估計模型 P（k|k）。

3 試驗分析

3.1 試驗設計

在室內環境中，定位目標經常要進行90°直角拐彎，本文對此要求在室內環境設計了路徑試驗對比檢驗傳統卡爾曼濾波與IMM濾波效果。首先，使用3基站1標簽采集定位數據。基站按三角形分布在（0，0），（0，3.8），（5.6，2.2）3 個空間固定坐標位置。試驗人員按設定路線從（0，1.4）開始沿x軸正方向運動4.8 m后轉90°沿y軸正方向運動2.4 m后再轉90°沿x軸負方向運動4.8 m（由于標簽由試驗人員手拿采集數據，得到的位置與預定軌道有一定的偏移），如圖4所示。試驗的采樣周期為0.1 s，在基站A0（0，0）處用USB數據線連接電腦通過串口調試助手對標簽到3基站的距離數據進行采集。使用式（3）～式（6）計算出所有坐標，并進行卡爾曼濾波。傳統卡爾曼濾波與IMM卡爾曼濾波效果如圖5所示。并對傳統卡爾曼濾波和IMM卡爾曼濾波做RMS分析，得到其誤差跟蹤圖，如圖6所示。

圖4 基站布置以及標簽移動路徑Fig.4 Base station layout and label moving path

圖5 傳統卡爾曼與IMM濾波觀測值軌跡和軌跡Fig.5 Observation trajectory and trajectory of traditional Kalman and IMM filtering

圖6 傳統卡爾曼與IMM濾波誤差跟蹤圖Fig.6 Traditional Kalman and IMM filtering error tracking map

3.2 試驗結果分析

從圖5可以觀察到，在沿x軸運動初期，卡爾曼濾波對目標誤差消除作用是非常明顯的，其曲線相比于觀測值更加平滑。但在x軸向y軸轉向和y軸向x軸兩次90°轉向之后的過程中，卡爾曼濾波值相對于觀測值都產生了“滯后”的現象，造成短時間內誤差值甚至大于觀測值。傳統卡爾曼濾波由于是建立在模型精確和隨機干擾信號統計特性已知的情況下，在卡爾曼濾波整個過程中干擾信號的統計學特征值保持不變[6]。然而，試驗人員在轉彎時突然的加速與減速使得干擾信號統計學特性發生了改變[7]。交互多模型采用多個卡爾曼濾波器并行處理，每個濾波器對應不同的狀態空間模型，不同的狀態空間模型描述不同的目標運動狀態，最后通過有效的加權融合進行系統估計，很好地克服了傳統卡爾曼濾波單模型估計誤差較大的問題。如圖5所示，在第一次y軸向x軸90°轉向之后，傳統卡爾曼濾波會逐漸恢復其功能，但短時間內會造成極大的誤差，如圖上第一次x軸向y軸轉向，x軸方向上的誤差最大接近50 cm。IMM濾波雖然在第一次轉彎的時候也產生了“滯后”現象，但相比較傳統卡爾曼濾波，其造成的誤差更小，并且收斂的速度明顯快于傳統卡爾曼濾波。并且從圖6傳統卡爾曼濾波與IMM濾波的誤差跟蹤圖中可以明顯看出，IMM的濾波效果要優于傳統卡爾曼濾波。

4 結語

采用UWB技術的室內定位有著精度高、功耗低、傳輸速率快、抗多徑干擾能力強等優點，目前基于UWB技術的定位多采用基于測量距離的定位方法[8]。本文介紹了基于飛行時間的雙向測距方法（TWTOF）的過程。對于室內環境中干擾多以及傳統卡爾曼濾波在目標機動時濾波效果不好的特點，本文提出使用交互多模型卡爾曼濾波的方法對定位坐標進行最優估計以降低誤差，并針對室內環境設計了試驗檢驗其效果。試驗結果顯示，交互多模型卡爾曼濾波能有效的減少誤差，在室內環境經常遇到的大轉角情況下，卡爾曼濾波效果雖然在短時間內仍會產生誤差，其濾波值誤差要高于觀測值，但其能更加快速的恢復濾波效果。總體上，交互多模型卡爾曼濾波對觀測值的優化效果十分顯著。

[1]楊洲.基于UWB/MEMS的高精度室內定位技術研究[D].徐州：中國礦業大學，2015.

[2]張桀，沈重.聯合TDOA改進算法和卡爾曼濾波的UWB室內定位研究[J].現代電子技術，2016，39（13）：1-5.

[3]邵磊.基于超寬頻距離傳感器的室內定位系統的研究與實現[D].北京：北京工業大學，2014.

[4]王磊，程向紅.基于期望模式修正的交互多模型組合導航算法[J].光學精密工程，2014，22（3）：737-744.

[5]Pelka M，Goronzy G，Hellbrück H.Iterative approach for anchor configuration of positioning systems[J].Ict Express，2016，2（1）：1-4.

[6]Zhang R，H?flinger F，Reindl L.TDOA-Based localization using interacting multiple model estimator and ultrasonic transmitter/receiver[J].IEEE Transactions on Instrumentation&Measurement，2013，62（8）：2205-2214.

[7]Hu C，Chen W，Chen Y，et al.Adaptive Kalman filtering for vehicle navigation[J].Journal of Global Positioning Systems，2003，2（1）：42-47.

[8]Abdulrahman A，Abdulmalik A S，Mansour A，et al.Ultra wideband indoor positioning technologies：analysis and recent advances[J].Sensors，2016，16（5）：1-36.