具變號非線性項三階多點邊值問題的正解與多個正解

沈春芳,楊 劉,解大鵬

(合肥師范學院數學系,安徽合肥 230601)

1　引言

本文研究如下三階常微分方程m點邊值問題

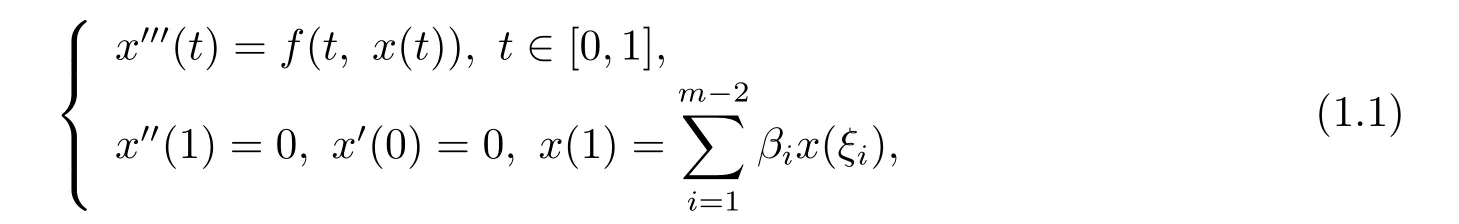
(H)f∈C([0,1]×[0,+∞),(?∞,+∞)),f(t,0)≥0,t∈[0,1]且不恒為0.

三階常微分方程邊值問題廣泛出現在流體力學、天文學、彈性振動等問題中[1],對相關問題正解的研究近年來受到人們廣泛的關注.利用非線性泛函分析方法,對三階微分方程邊值問題正解與多個正解的存在性的研究取得了豐富的結果,可參考文獻[2–12].Anderson[2]研究如下三階三點邊值問題

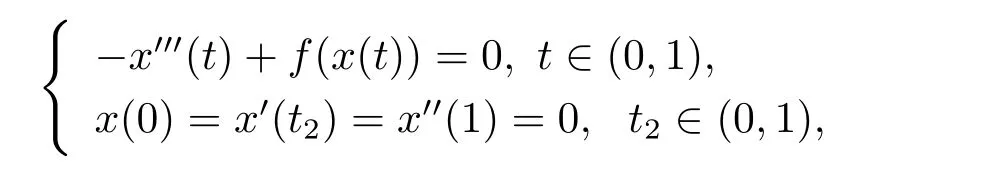
其中f:R→ [0,+∞)連續,1/2≤t2＜1,文中建立了問題至少三個正解的存在性結果.Palamides[3]利用范數形式的錐拉伸錐壓縮不動點定理,證明了三階三點邊值問題

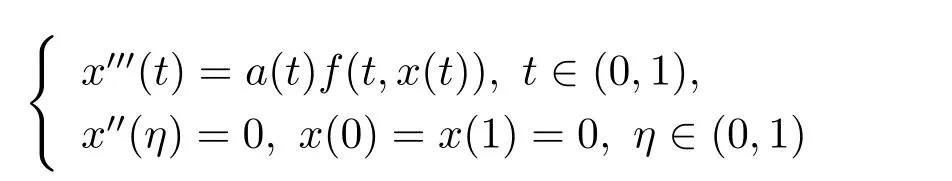
多個正解的存在性.Guo[5]利用錐上不動點定理證明了三階三點邊值問題

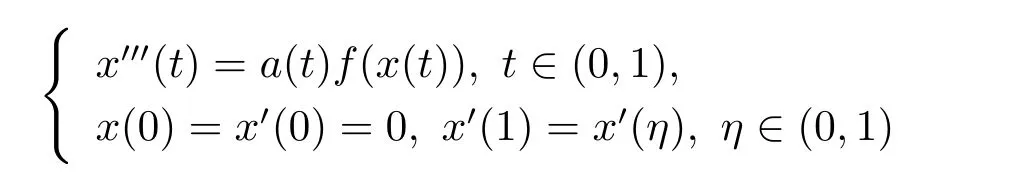
正解的存在性,其中f非負且滿足超線性或次線性條件.但在這些文獻中,均要求問題中非線性項非負,非線性項變號時,所得結論不再適用.目前,對具變號非線性項的三階常微分方程多點邊值問題正解的討論比較少見.本文首先建立與問題(1.1)等價的算子方程,利用錐上不動點定理,給出了問題(1.1)正解與多個正解的存在性結論.文中允許非線性項變號,因此所得結果不同于已有文獻.最后,文中給出了具體的例子解釋了結論的應用性.

2　預備知識

定義2.1設E為實Banach空間.非空閉凸集P?E稱為E上的錐,如果滿足

(1)au∈P,對u∈P,a≥0;

(2)u,?u∈P,u=0.

定義2.2函數x稱為[0,1]上的凸泛函,如果

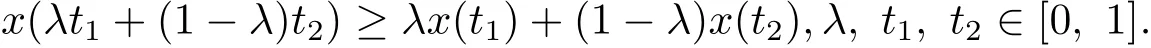
引理2.1(見文獻[14])設K是Banach空間X上的錐,D為X上有界開子集,滿足設全連續且x/=Ax對x∈?DK,有如果iK(A,DK)=1,iK(A,UK)=0或iK(A,DK)=0,iK(A,UK)=1,則A在

(1) 如果‖Ax‖≤ ‖x‖,x∈ ?DK,則iK(A,DK)=1.

(2)若存在e∈K{0}使得x/=Ax+λe,x∈?DK,λ＞0,則iK(A,DK)=0.

(3)設U是X中有界開集中至少有一不動點.

3　主要結果與證明

首先考慮三階微分方程邊值問題

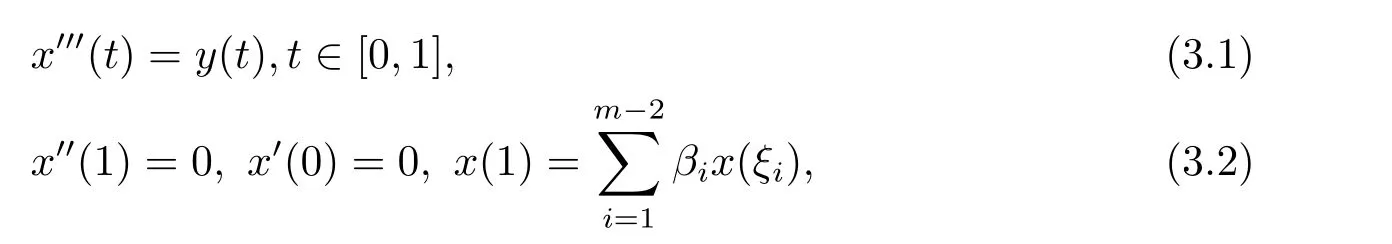
引理3.1記ξ0=0,ξm?1=1,β0= βm?1=0,y(t)∈ C[0,1],問題(3.1),(3.2)等價于

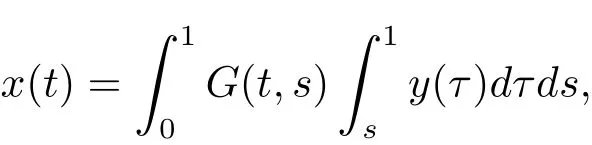
其中

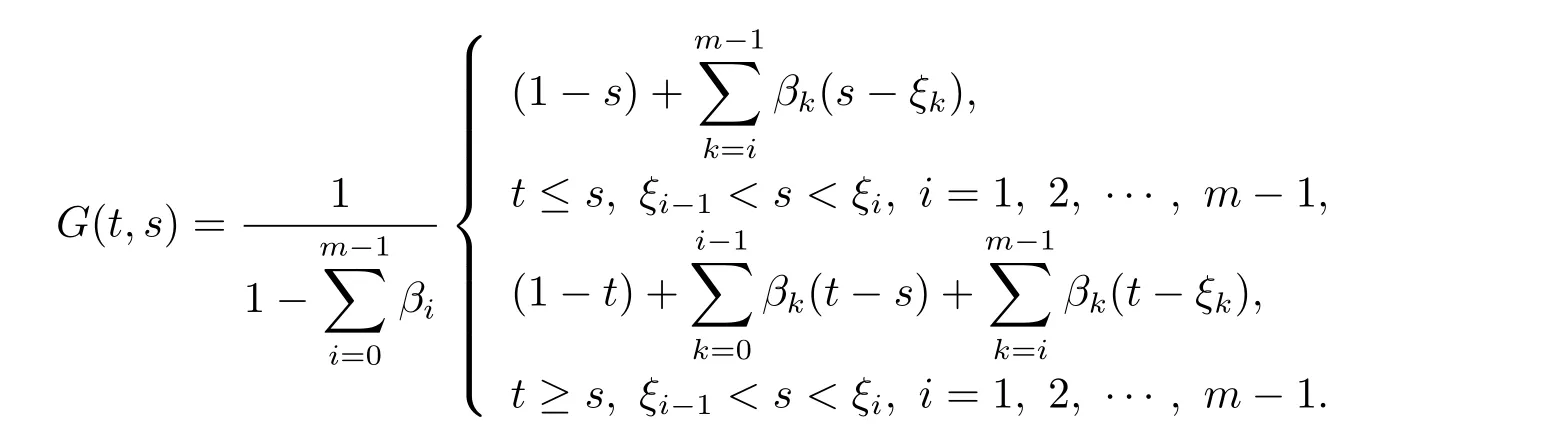
證(3.1)式兩側積分并考慮條件x′′(1)=0,有

設G(t,s)是邊值問題

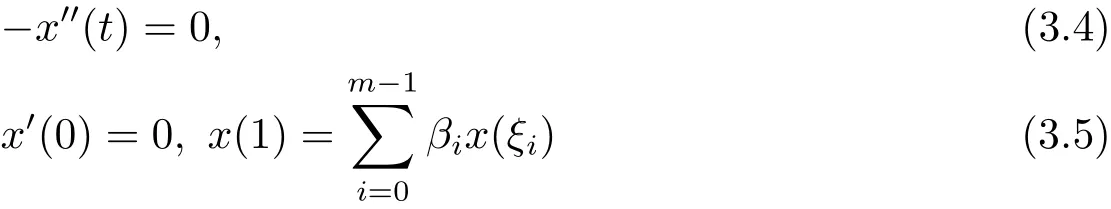
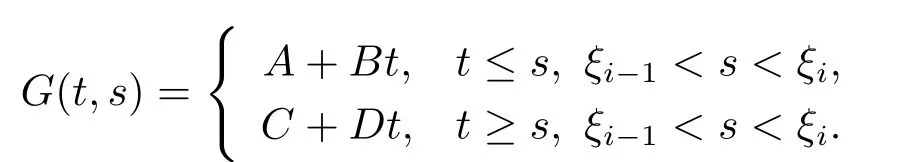
的Green函數,由(3.4)式,可設由Green函數定義及性質,結合邊值條件(3.5),有

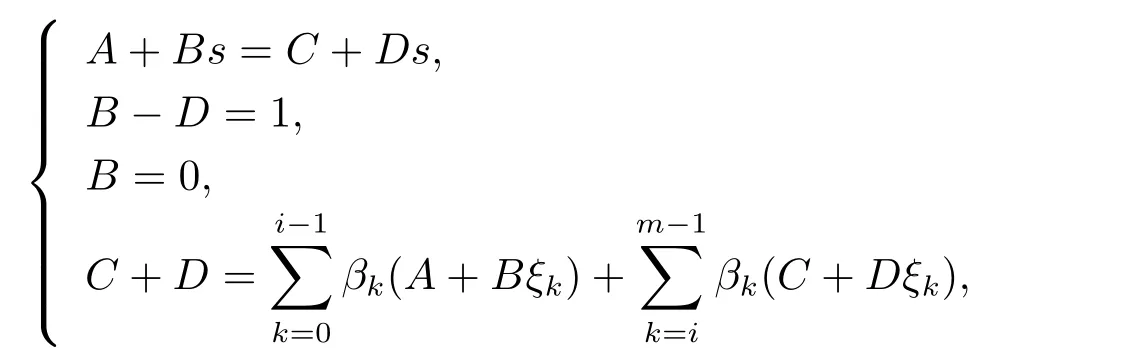
這樣

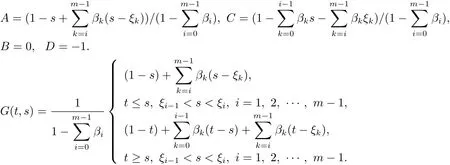
考慮(3.3)式,問題(3.1),(3.2)等價于

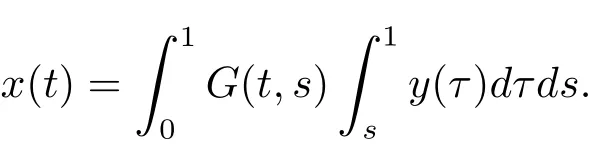
引理3.2函數G(t,s)滿足G(t,s)≥0,t,s∈[0,1].

證對 ξi?1≤ s ≤ ξi,i=1,2, ···,m ?1,t≤ s,

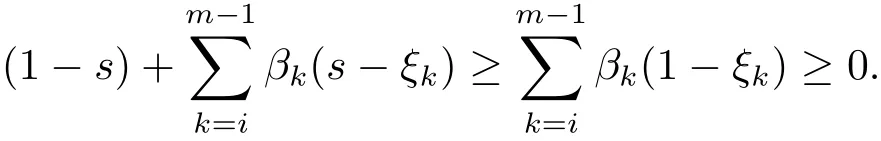
對 ξi?1≤ s ≤ ξi,i=1,2, ···,m?1,t≥ s,

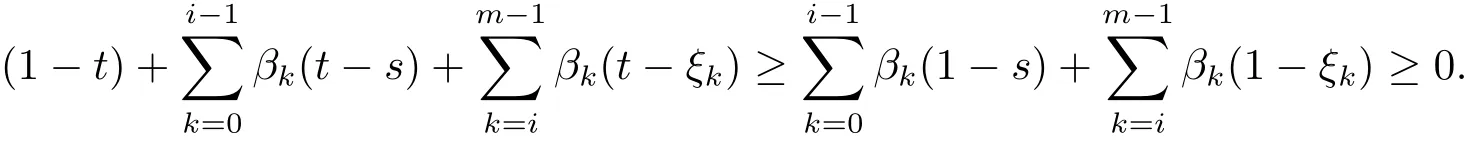
綜上,G(t,s)≥0,t,s∈[0,1].

引理3.3設y(t)≥0,t∈[0,1],x(t)是邊值問題(3.1),(3.2)的解,則有

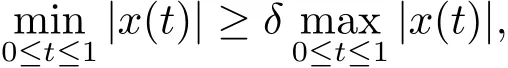
其中

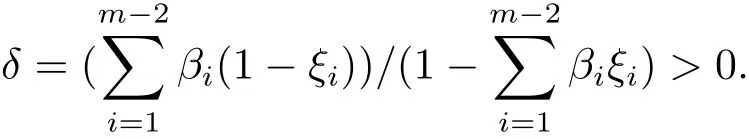
證由 x′′′(t)=y(t) ≥ 0,t ∈ [0,1]知 x′′(t) 在 [0,1]上單調遞增.考慮到 x′′(1)=0,有x′′(t)≤ 0,t∈ (0,1). 結合 x′(0)=0,必有

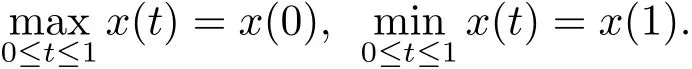
由x(t)的凸性,

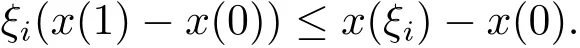
上式兩端乘以βi,i=1,2,···,m?1,結合邊值條件,有

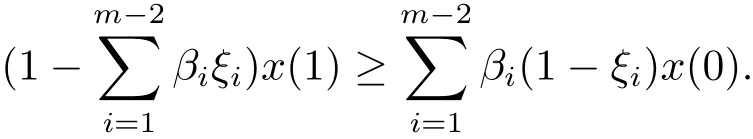
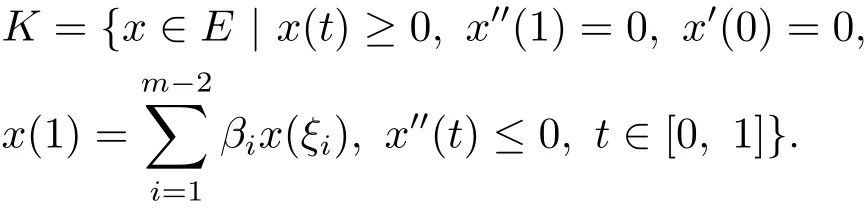
定義

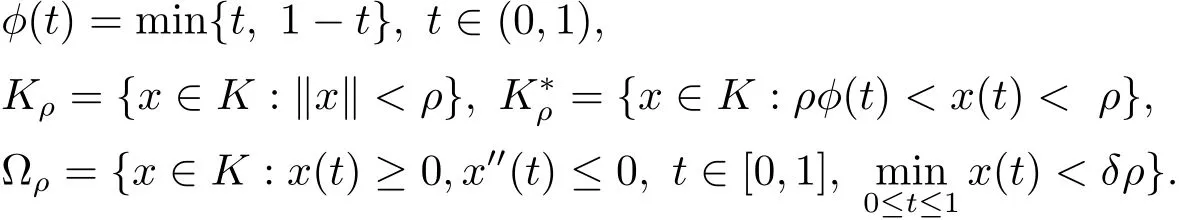
引理3.4?ρ具有如下性質:

(1)?ρ?Kρ是Kρ中開集.

(2)設x∈ ??ρ,則δρ≤ x(t)≤ρ,t∈[0,1].

記

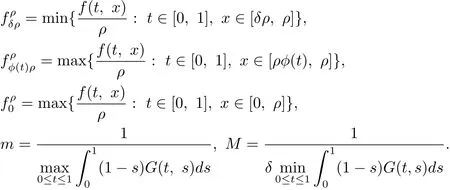
定理3.1假定條件(H)成立.此外,若條件(H1)成立:

(H1) 存在正常數ρ1,ρ2,ρ3∈ (0,∞)滿足ρ1＜ δρ2＜ ρ2＜ ρ3使得

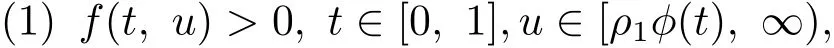
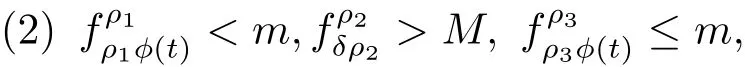
則問題(1.1)在K 中至少有三個解.假定條件(H)成立.此外,若條件(H2)成立:

(H2)存在正常數ρ1,ρ2,ρ3∈(0,∞)滿足ρ1＜ρ2＜ρ3使得

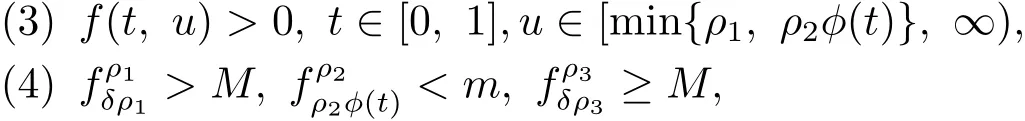
則問題(1.1)在K中至少有兩個解.

證 首先設條件(H1)成立.定義輔助函數f?(t,x)∈C([0,1]×[0,∞),[0,∞)):

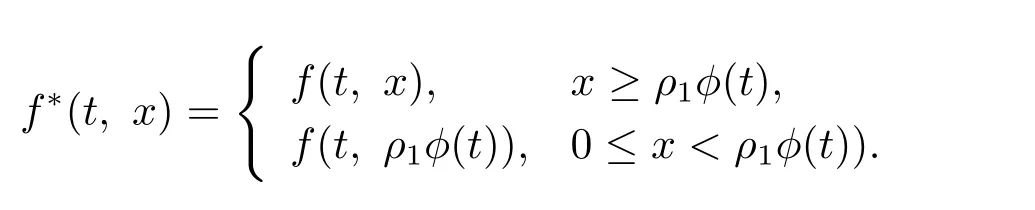
考慮如下輔助邊值問題

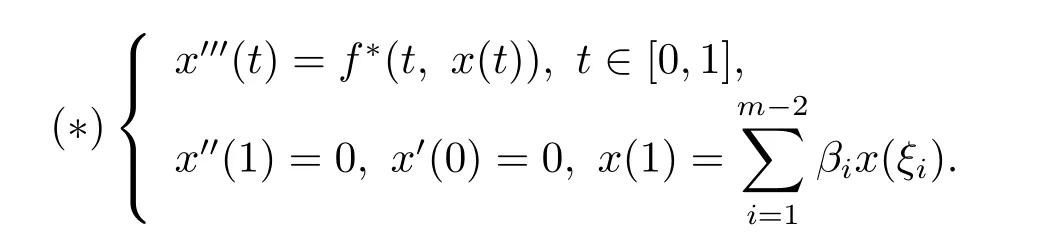
定義算子

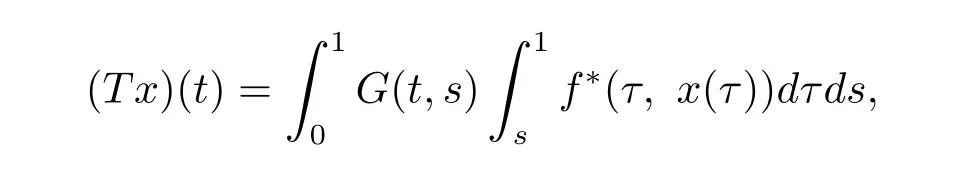
顯然T:K→K是全連續的.由條件(H1),有

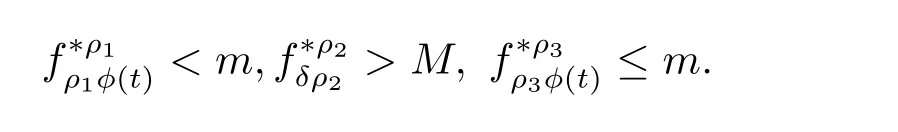
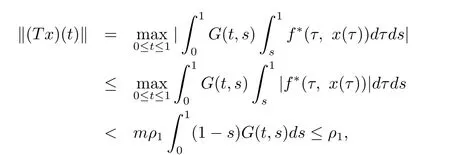
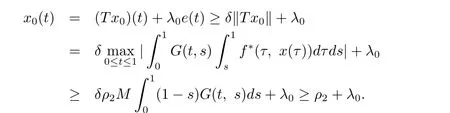
這表明ρ2≥ρ2+λ0,矛盾.由引理2.1,iK(T,?ρ2)=0.同理可證這樣,輔助邊值問題存在三個正解x1,x2,x3使得

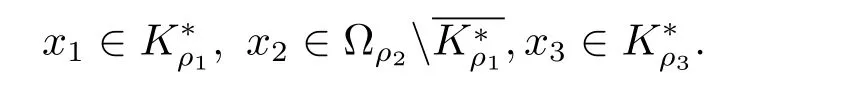
易驗證輔助邊值問題(?)在[ρ1φ(t),∞)中存在三個正解x1,x2,x3,這說明邊值問題(1.1)存在至少三個正解.條件(H2)成立時,正解的存在性同理可證.完全類似定理3.1,可證得如下結論.

定理3.2設條件(H)成立.此外,下列條件之一成立:

(H3)存在正常數ρ1,ρ2∈(0,∞)滿足ρ1＜δρ2使得

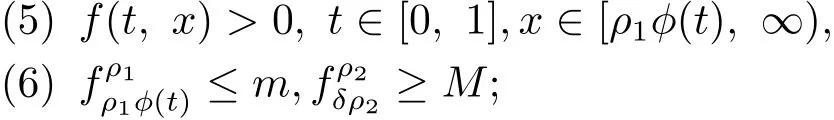
(H4)存在正常數ρ1,ρ2∈(0,∞)滿足ρ1＜ρ2使得

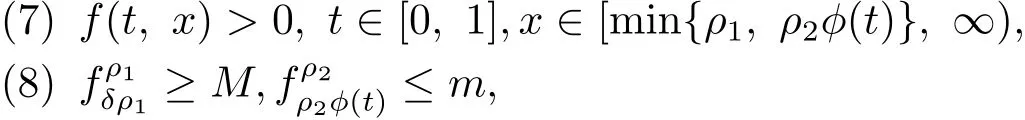
則邊值問題(1.1)在K中至少有一正解.

4　例子

考慮如下三階四點邊值問題

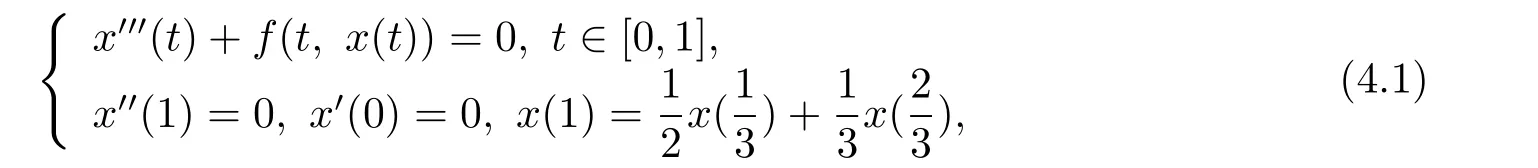
其中

計算可得函數G(t,s)由下式給出

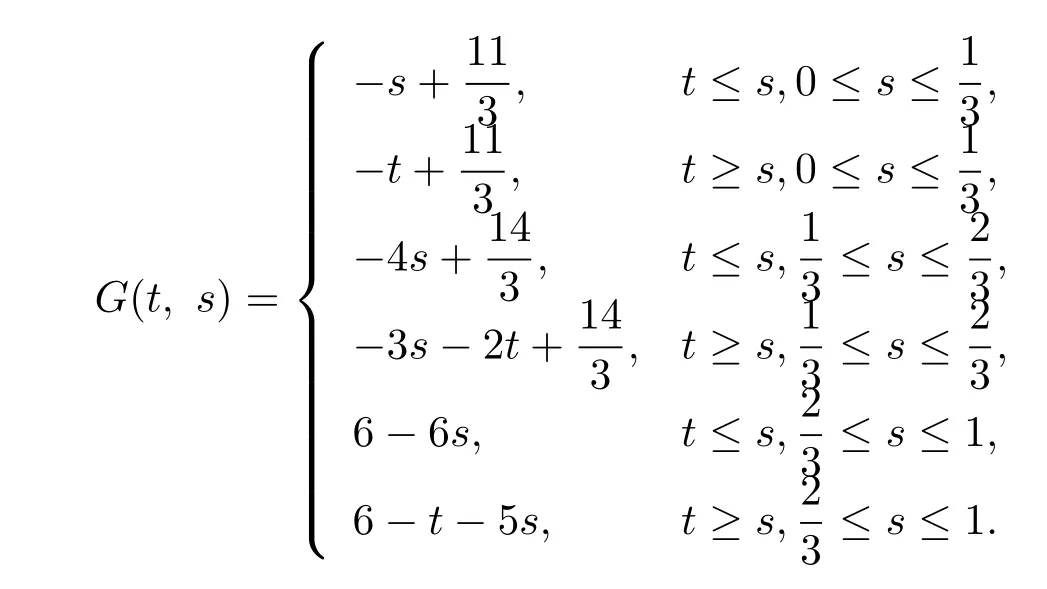
取 ρ1=1,ρ2=11, ρ3=122,有易驗證f(t,x)滿足條件(H)和

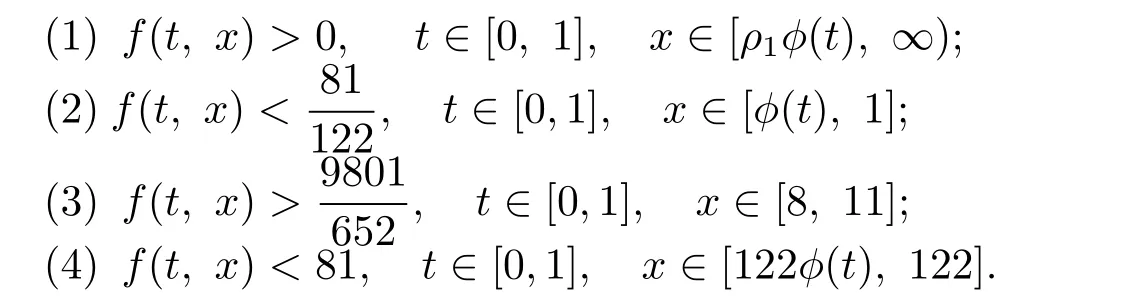
這樣定理3.1的所有條件均滿足,因此,問題(4.1)至少存在三個單調遞增的凸正解.

注 問題(4.1)中非線性項是變號的,已有文獻中對三階邊值問題正解存在性的討論,就作者所知,均無法適用此問題.

[1]Gregus M.Third order linear differential equations[J].Math.Appl.,Reidel,Dordrecht,1987,11(3):919–944.

[2]Anderson D R.Multiple positive solutions for a three-point boundary value problem[J].Math.Comput.Model.,1998,27(6):49–57.

[3]Palamides P,George Smyrlis.Positive solutions to a singular third-order three-point boundary value problem with an indefinitely signed Green’s function[J].Nonl.Anal.,2008,68:2104–2118.

[4]Guo D,Lakshmikantham V.Nonlinear problems in abstract cones[M].New York:Academic Press,1988.

[5]Guo L,Sun J,Zhao Y.Existence of positive solutions for nonlinear third-order three-point boundary value problems[J].Nonl.Anal.,2008,68:3151–3158.

[6]Hopkins B,Kosmatov N.Third-order boundary value problems with sign-changing solutions[J].Nonl.Ana.,2007,67:126–137.

[7]Chu J,Zhou Z.Positive solutions for singular non-linear third-order periodic boundary value problems[J].Nonl.Ana.,2006,64:1528–1542.

[8]Graef J,Kong L.Positive solutions for third order semipositone boundary value problems[J].Appl.Math.Lett.,2009:22:1154–1160.

[9]Lin X,Du Z,Liu W.Uniqueness and existence results for a third-order nonlinear multi-point boundary value problem[J].Appl.Math.Comput.,2008,205:187–196.

[10]Minghe P,Chang S.Existence and uniqueness of solutions for third-order nonlinear boundary value problems[J].J.Math.Anal.Appl.,2007,327:23–35.

[11]Li S.Positive solutions of nonlinear singular third-order two-point boundary value problem[J].J.Math.Anal.Appl.,2006,323:413–425.

[12]Yao Q.Positive solution for a semi-linear third-order two-point boundary value problem[J].Appl.Math.Lett.,2004,17:1171–1175.

[13]Ji D,Feng M,Ge W.Multiple positive solutions for multipoint boundary value problems with sign changing nonlinearity[J].Appl.Math.Comput.,2008,196:511–520.

[14]Lan K Q.Multiple positive solutions of semi-linear differential equations with singularities[J].J.London Math.Soc.,2001,63:690–704.