基于Lasserre松弛的緊約束多項式優(yōu)化問題逼近界分析

高雷阜,周 慶

(遼寧工程技術大學優(yōu)化與決策研究所,遼寧阜新 123000)

1　引言

多項式優(yōu)化問題(POP)可描述為目標函數(shù)和約束條件都用多項式表示的一類優(yōu)化問題,是全局優(yōu)化中的一個基本而重要的研究對象,已被廣泛應用于信號處理和系統(tǒng)控制等領域.近年來,這類問題吸引了大批學者的關注,產生了豐富的研究成果[1,2].POP的求解是一個頗具挑戰(zhàn)性的問題,傳統(tǒng)的數(shù)值求解方法有最速下降法、牛頓法、擬牛頓法、共軛梯度法、信賴域法等[2?8].但POP一般是非凸的,故用這些方法求出的值不一定是全局最優(yōu)值,大多情況下只是局部最優(yōu)值.

POP的數(shù)學形式如下

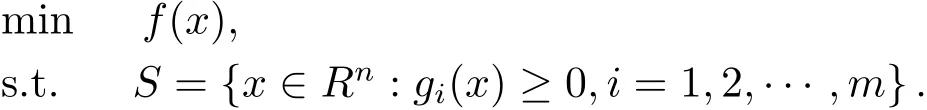
當約束集合是緊集時,其退化為緊約束POP.此類問題是NP難的,不易求解.經典求解采用Lagrange松弛方法,將其松弛成一個凸優(yōu)化問題.近年來,Lasserre提出了一種求解POP的全局優(yōu)化算法[2],該方法是基于半定規(guī)劃(SDP)松弛,能無限逼近問題的全局最優(yōu)值.目前該方法已廣泛應用于多個領域[2?6].此方法被相關學者稱為Lasserre松弛方法.

本文主要研究緊約束POP,基于上述松弛思想,結合多項式平方和(SOS),利用Lasserre將原緊約束POP轉化為SOS形式及其成立條件,給出其成立條件推導SOS式成立的證明.在進一步轉化為求解另一SOS問題的基礎上,給出當其矩陣特征值的最小值大于0時,上述條件成立的證明.從而找出其目標函數(shù)在約束集合的下界,通過給出的理論,估計出下界與最小值相差的距離,即逼近界.最后,文章將原有的逼近界定理進一步轉化,給出了新的逼近界定理.

2　預備知識

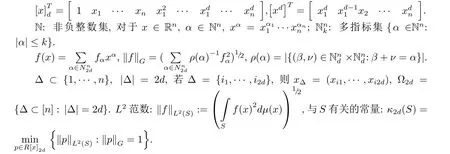
引理2.1[3]對于一個階數(shù)為2d的多項式f,存在一個對稱矩陣F,有

引理2.2[3?5]f是其中F≥0.

3　問題及主要結果

考慮如下POP

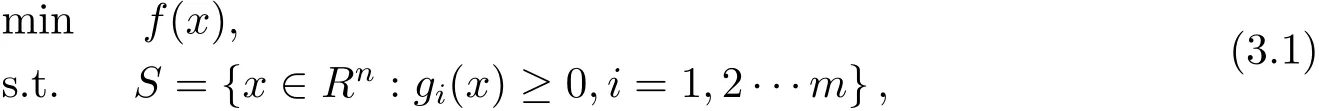
其中S是緊集,f,g1,···,gm的階數(shù)不大于2d(稱d為松弛階數(shù)),(3.1)式不易求解,因此

Lasserre將其轉化成如下SOS形式去找(3.1)式中fmin的下界[2]

其中deg表示多項式的階數(shù),fmin(fmax)表示f在S上的最小值(最大值),fsos表示(3.2)式中的最優(yōu)值.由上述知,對于固定的d,有fsos≤fmin.當g1,···,gm在適當?shù)臈l件下,存在Q=Q(g1,···,gm)有

為了保證(3.2)式成立,需如下引理.

引理3.1[6]存在一個對稱的正定矩陣E 及SOS多項式σ1,···,σm,且deg(σigi)≤2d,i=1,···,m,有

定理3.1若S內部非空,R[x]是實多項式環(huán),R[x]k表示階數(shù)最多是k的多項式的子空間,那么下列敘述等價

(1)引理3.1成立;

(2)對于每個f∈R[x]2d,(3.2)式都可求;

證(1)?(2)由引理2.1,有其中F是對稱矩陣.由引理3.1知E是正定矩陣,因此存在足夠大的λ,且λ＞0,使

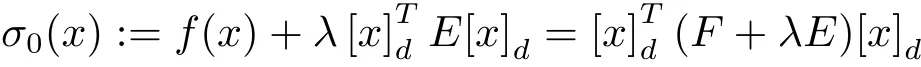
(2)?(3)顯然成立.

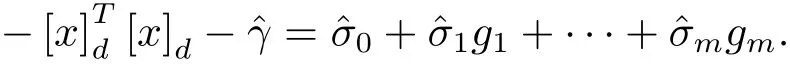
因此引理3.1成立.故定理3.1成立.

在引理3.1中,多項式σ1,···,σm和正定矩陣E 可能并不唯一.當λmin(E)越大,獲得的逼近界越好.其中X 是對稱矩陣,λmax(X)(λmin(X))表示X 的特征值的最大值(最小值),X＞0意味著λmin(X)＞0.因此盡可能找到λmin(E)的最大值,進而解決如下SOS問題

定理3.2假設是(3.4)式的最優(yōu)解.當且僅當λmin(E?)＞0,引理3.1才成立.

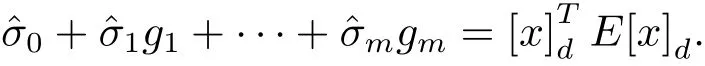
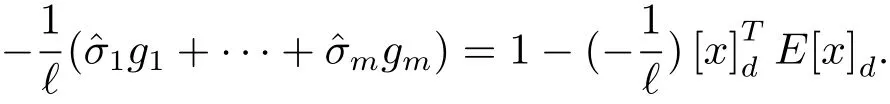
故結論得證.

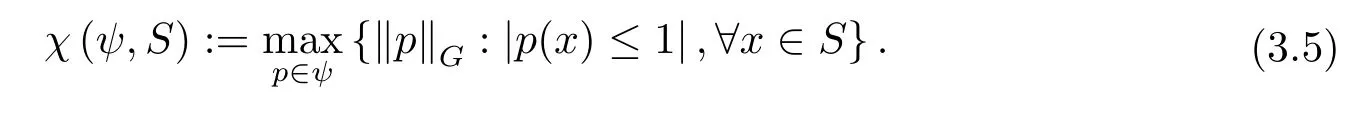
引理3.2[9]若S內部非空,對于每個?∈?2d,且0在S內部,則κ2d(S)＞0.

引理3.3[10]如果f∈R[x]2d,那么存在一個對稱矩陣W,使得

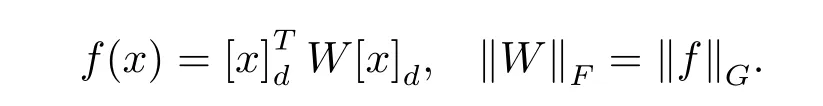
其中對于任意矩陣A,‖A‖2是標準的二范數(shù),注意 ‖A‖2≤ ‖A‖F(xiàn).

引理 3.4[11]假設ψ 是包含1的R[x]2d的子空間,χ(ψ,S)＜ ∞,(σ1,···,σm,E)滿足引理3.1.令f∈ψ,fmin(fmax)是在S上的最小值(最大值).如果fsos是(3.2)式的最優(yōu)值,則有

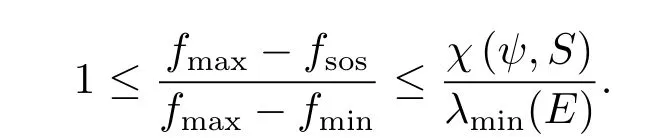
為了得到引理3.4的精確的逼近界,需要估計χ(ψ,S)和λmin(E)的值.

定理3.3假設0在S 的內部,(σ1,···,σm,E)滿足引理3.1,令f∈R[x]2d,則有

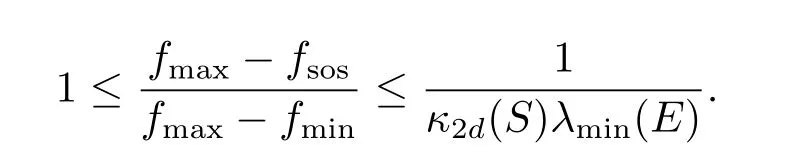
證因為S內部非空,由引理3.2知如果

對所有的x∈ S 都有|p(x)|≤ 1,則‖p‖L2(S)≤ 1.由有由引理3.4得

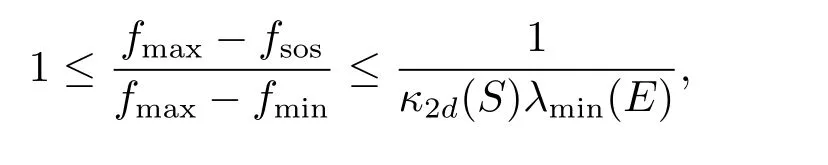
故定理得證.

注如果(3.4)式中的最優(yōu)解用到上式,獲得的最優(yōu)界更好.(3.4)式中的最優(yōu)值λmin(E?)的選取依賴于S.已有文獻給出但未給收斂性.下面給出具體過程并證明收斂.

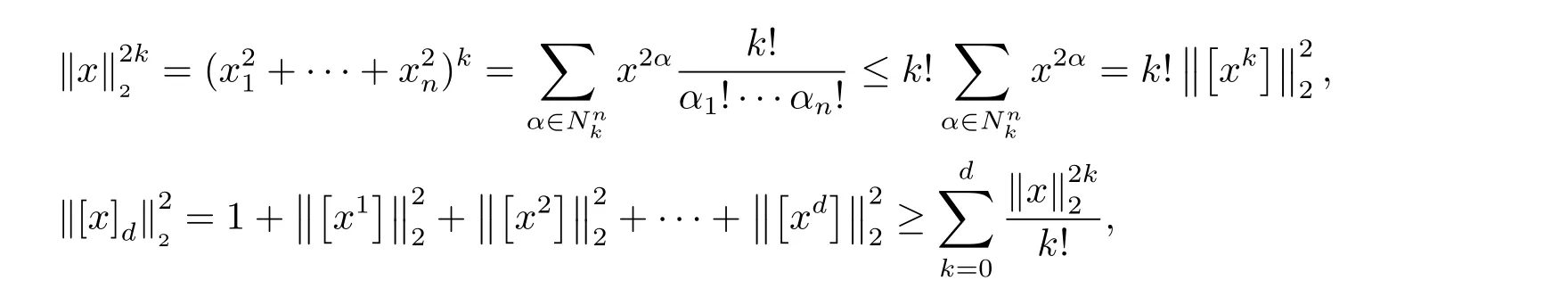
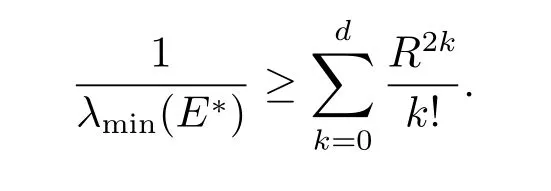
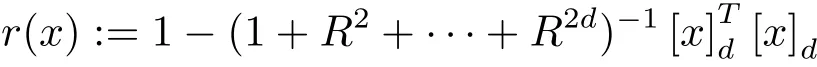
在S上非負.若存在SOS多項式s0,s1,···,sm,對每個deg(sigi)≤2d及

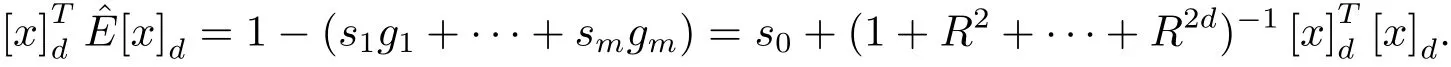
因為s0是SOS,有

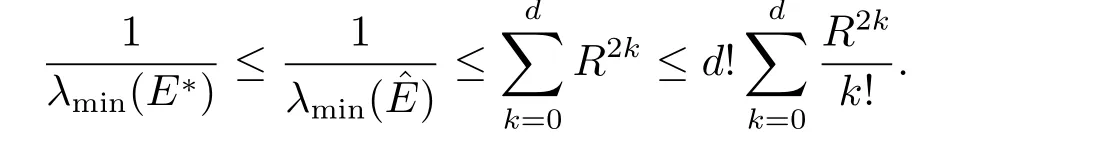
所以如果(3.6)式成立,則有

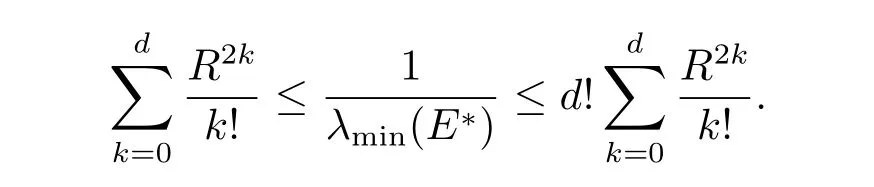
如果(3.6)式不成立,但已知R,可以增加(3.1)式的約束條件r(x)≥0.故可以通過來估計.下證其收斂性.

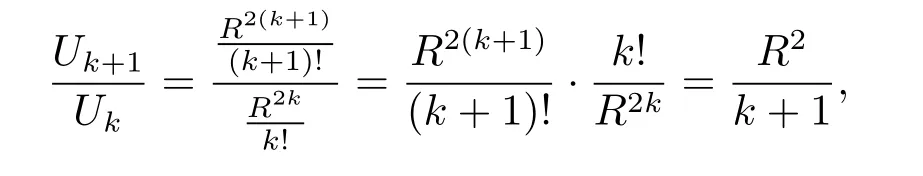
有

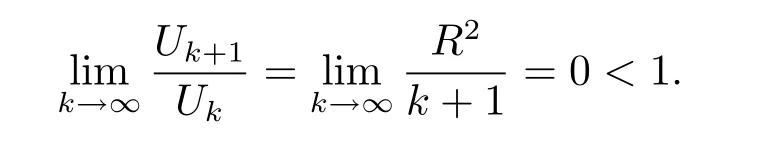
4　結論

緊約束POP是NP難的,不易求解,故Lasserre將其轉化為SOS形式求目標函數(shù)在約束集合的下界.為了使得Lasserre轉化的SOS可求,在已知其成立條件前提下,進一步給出證明過程,從而找出所求問題的下界.在已知下界的基礎上,通過理論估計出下界與最小值相差的距離,即逼近界.將原有的逼近界定理進行轉化,給出另外一個逼近界定理,從而解決原緊約束POP.

[1]陳德俊.多項式優(yōu)化方法在二次規(guī)劃問題中的應用[D].北京:清華大學,2011.

[2]Lasserre J B.Global optimization with polynomials and the problem of moments[J].Soc.Indus.Appl.Math.,2001,11(3):796–817.

[3]Prajna S,Papachristodoulou A,Wu F.Nonlinear control synthesis by sum of squares optimization:A Lyapunov-based approach[C].Proc.Asian Contr.Conf.,2004,1:157–165.

[4]Parrilo P A.Semidefinite programming relaxations for semialgebraic problems[J].Math.Prog.,2003,96(2):293–320.

[5]Laurent M.Sum of squares,moment matrices and optimization over polynomials[J].Emer.Appl.Alg.Geom.,2008,149:157–270.

[6]Lasserre J B.Moments,positive polynomials and their applications[M].London:Imperial College Press,2009.

[7]董麗,周金川.無約束優(yōu)化問題的一個下降方法[J].數(shù)學雜志,2015,35(1):173–179.

[8]張新華.等式約束非凸優(yōu)化問題的修正牛頓算法[J].數(shù)學雜志,2015,35(1):1–11.

[9]Barvinok.Eastimating L∞norms by L2knorms for functions on orbits[J].Found.Comp.Math.,2002,2(4):393–412.

[10]Nie J,Demmel J,Sturmfels B.Minimizing polynomials via sum of squares over the gradient ideal[J].Math.Prog.,2005,106(3):587–606.

[11]Reznick B.Some concrete aspects of Hilbert’s 17th problem[J].Contem.Math.,Amer.Math.Soc.,2000,253:251–272.