長大下坡道區(qū)間地鐵列車節(jié)能操縱方法
柏 赟,周雨鶴,邱 宇,賈文崢,毛保華
(1.北京交通大學 城市交通復雜系統(tǒng)理論與技術(shù)教育部重點實驗室,北京 100044;2.交通運輸部 科學研究院, 北京 100029)
由于地鐵具有安全、準點、環(huán)保等特點,近年來得到了快速發(fā)展。在建設里程和客運量增長的同時,地鐵系統(tǒng)的能耗也在迅速上升。列車運行能耗占地鐵系統(tǒng)總能耗的50%左右。通過合理的操縱方法降低運行能耗,對降低運營成本、促進可持續(xù)發(fā)展有重要的現(xiàn)實意義。
列車運行控制節(jié)能優(yōu)化問題是指在給定的線路條件、信號系統(tǒng)和運行時分下,研究使牽引能耗最小的列車操縱方法。FIGUERA[1]證明了列車在平緩區(qū)間內(nèi)的節(jié)能操縱包括牽引、惰行和制動3種工況。隨后LEE等[2]和ASNIS等[3]證明了列車在較長區(qū)間內(nèi)運行時還存在巡航工況。HOWLETT[4]基于極大值原理證明了平直線路上的列車最優(yōu)操縱應包含最大牽引、巡航—惰行、最大制動4個階段,并給出了各工況轉(zhuǎn)換點的求解方法。王青元等[5]給出了低于限速及觸及限速時的最優(yōu)控制工況間的最優(yōu)切換規(guī)則,以及操縱工況間最優(yōu)的切換時機。荀徑等[6]考慮了多列車相互影響條件下的列車運行控制最佳策略。丁勇等[7]研究了在起伏坡道和定時約束條件下的列車節(jié)能運行控制方法,建立了站間惰行次數(shù)和惰行點的優(yōu)化模型并用遺傳算法進行求解。牟瑞芳等[8]針對高速動車組優(yōu)化操縱問題,利用廣義乘子法搜索目標速度值及對應的速度集合,將有約束非線性規(guī)劃求解問題轉(zhuǎn)化為無約束極值求解問題。當列車運行在陡下坡區(qū)段時,楊杰等[9]提出平均速度等效的處理方法,即通過陡坡區(qū)段所消耗的時間等于以平均速度通過該區(qū)段所消耗的時間。張守帥等[10]針對CTCS-2級列控系統(tǒng)下高速列車在長大下坡地段運行的情形,對車載設備參數(shù)取值及監(jiān)控制動距離的計算方法進行優(yōu)化。HOWLETT等人[11]對干線鐵路貨物列車在長大坡道的節(jié)能操縱進行了研究,基于極大值原理研究了列車在長大坡道上的節(jié)能操縱方法。雖然有學者對長大坡道上的列車操縱方法進行了研究,但是其研究對象主要是在下坡段無法維持巡航的貨物列車。而地鐵列車擁有更好的牽引制動性能,且其牽引質(zhì)量較小,一般不存在無法保持巡航的情況,因此在下坡段既使用制動、又保持巡航并不是最節(jié)能的操縱方法。因此,有必要對列車在長大下坡的操縱方法進行優(yōu)化。
本文在標準四階段操縱方法的基礎上,通過進一步優(yōu)化操縱工況序列及其轉(zhuǎn)換點,減少地鐵列車(簡稱列車)在長大下坡道上制動的時間,并充分利用坡道勢能為列車加速,從而減少牽引能耗。
1 問題描述和改進
圖1標準四階段操縱方法與改進操縱方法下的列車速度位移曲線示意圖
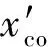
針對標準四階段操縱方法在長大下坡無法充分利用坡道勢能的不足,本文提出了改進操縱方法。該操縱方法由最大牽引、巡航—惰行、最大制動工況組成,其中巡航—惰行工況根據(jù)線路條件及列車運行狀態(tài)可以多次出現(xiàn),允許列車在惰行工況下達到限速時再次轉(zhuǎn)入巡航工況,當駛離大下坡或與終點的制動反推曲線相交時退出巡航工況。改進操縱方法下的列車速度位移曲線如圖1中的實線所示。圖1中,xcr和xco分別為改進操縱方法中開始巡航和初次惰行的起始位置,是改進操縱方法中的決策變量。vcr為改進操縱方法下的牽引末速度,在使用最大牽引力的情形下由xcr決定。改進操縱方法中可能出現(xiàn)多次惰行或巡航以適應坡道的變化,因此用xco-cr和xcr-co來表示后續(xù)工況的轉(zhuǎn)換位置。
與標準四階段速度曲線相比,采用改進速度曲線后列車只需牽引至較低速度vcr,巡航至xco后開始惰行并在xco-cr處達到限速,再次轉(zhuǎn)入巡航,在xcr-co處駛離長大下坡,之后由巡航轉(zhuǎn)入惰行,最后與制動曲線交于xbr處。相比標準四階段操縱方法,改進操縱方法以更低的速度進入巡航,并提升惰行工況的比例、減少巡航階段下列車采取制動工況的時間,可以實現(xiàn)牽引節(jié)能。
2 模型構(gòu)建
改進操縱方法的決策變量為使用最大牽引力的牽引終止位置xcr和初次巡航終止位置xco;優(yōu)化目標為列車運行總牽引能耗最小。總牽引能耗可表示為
(1)
式中:E為總牽引能耗,k·Wh;F(v,x)為列車以速度v運行在x處所需要的外力矢量,kN;θ為單位換算系數(shù),取3 600。
外力矢量F(v,x)用于衡量列車在運行過程中所受牽引力或制動力的大小,既有大小也有方向。由于牽引力和制動力不同時存在,且牽引力做正功,制動力阻礙運動做負功。因此,矢量外力的正負和數(shù)值分別代表牽引力或制動力及其大小,該外力矢量的取值范圍為
F(v,x)∈[-Fbr(v),Ftr(v)]
x∈[xstart,xend]
(2)
式中:Fbr(v)為列車在速度v時所能獲得的最大制動力,kN;Ftr(v)為列車在速度v時所能獲得的最大牽引力,kN。
由于列車在運行過程中存在多種工況,且每種工況的外力矢量均有不同,因此在確定決策變量xcr和xco后,需要根據(jù)運行狀態(tài)的變化,計算列車在各距離步長下的外力矢量F,為
(3)
其中,
式中:Fcr(v,x)為列車以速度v在x處保持巡航所需的外力矢量,kN;xbr為地鐵列車轉(zhuǎn)入最大制動工況轉(zhuǎn)換點;η(x)為運行狀態(tài)變量;FR(v,x)為列車以速度v在x處行駛所受到的阻力;vlim(x)為列車在x處的限速;s為距離的步長。
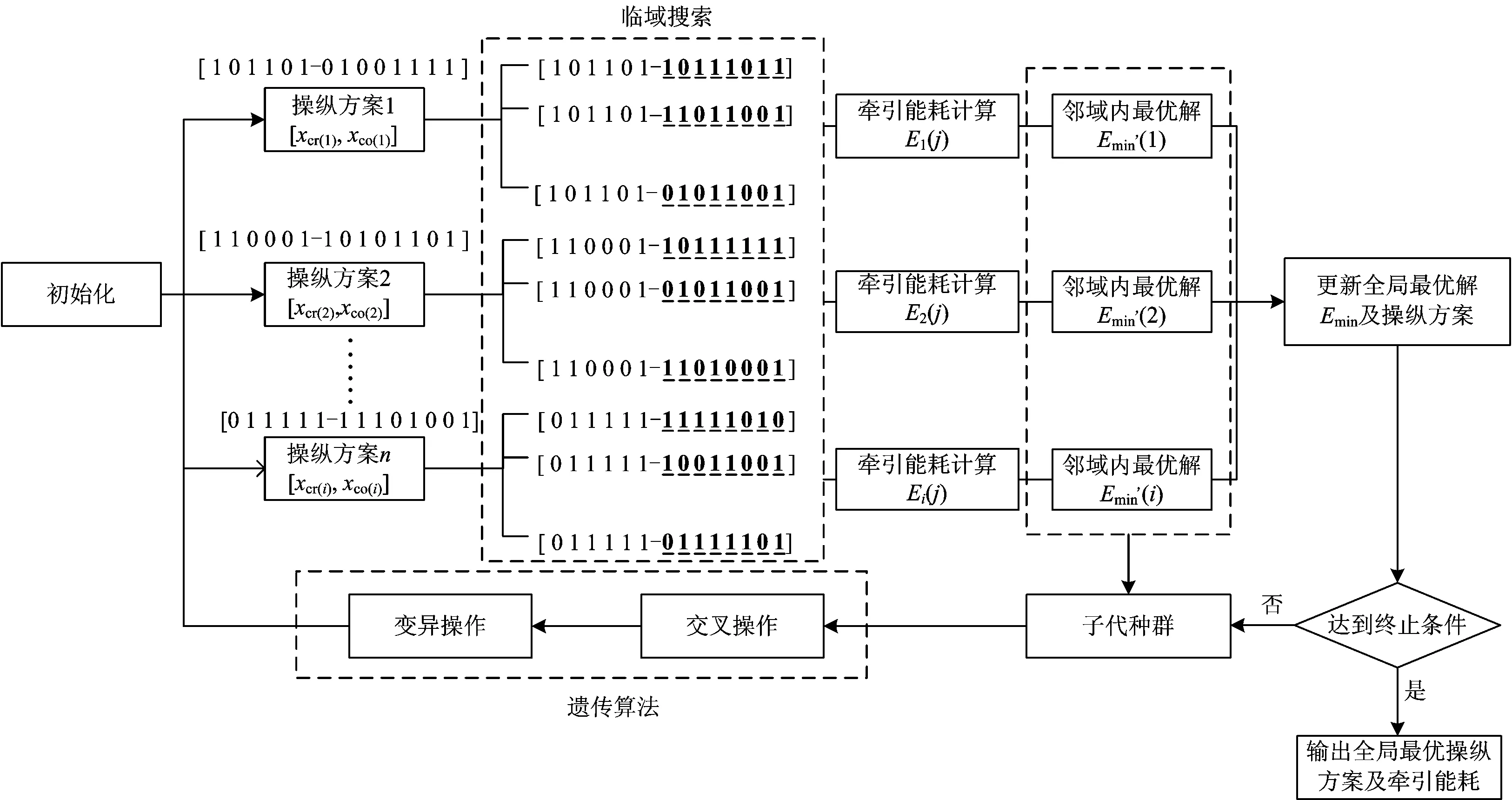
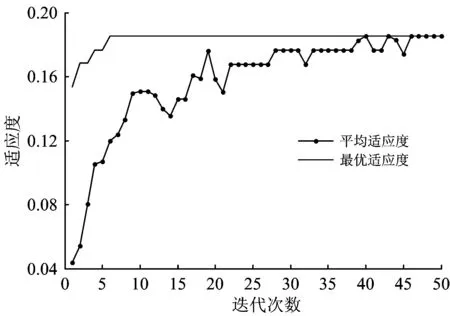
在出站牽引和進站制動階段,外力矢量F分別為列車最大牽引力和制動力;在途中運行階段,工況序列及持續(xù)時間的不確定性給模型求解和能耗計算帶來了一定難度。因此,在式(3)中引入變量η(x)表示列車在xco 當列車處于惰行工況時,外力矢量為0。當列車處于巡航工況時,需要根據(jù)列車受力情況計算外力矢量。列車在各運行狀態(tài)下所受合力Ftotal(v,x)為 Ftotal(v,x)=F(v,x)-FR(v,x) (4) 其中, FR(v,x)=Fgrad(x)+Fv(v)+Fc(x) Fgrad(x)=1 000sinθ Fv(v)=a+bv+cv2 式中:Fgrad(x)為坡道附加力;θ為x處的坡度,上坡為正,下坡為負;Fv(x)為基本阻力;a,b和c為列車基本阻力系數(shù);Fc(x)為曲線附加阻力;rx為x處的曲線半徑。 當列車處于巡航工況時其所受合力為零,此時的外力矢量在數(shù)值上等于阻力之和,即 (5) 列車在區(qū)間運行時還應該滿足計劃運行時分、列車限速等約束條件,為 (6) 式中:v(x)為列車在位置x處的速度,列車在運行區(qū)間起終點的速度應為0且在運行途中不超過限速;T為區(qū)間內(nèi)的給定運行時分;δ為運行時分的允許誤差。 列車操縱優(yōu)化是一個復雜的非線性優(yōu)化問題,難以直接采用解析方法進行求解。遺傳算法(Genetic Algorithm)作為一種全局搜索方法,具有簡單、魯棒性強等特點,在此類問題中應用廣泛。然而,在有限的迭代次數(shù)內(nèi)遺傳算法并不能保證獲得解的質(zhì)量。因此,本文在遺傳算法的基礎上加入鄰域搜索模塊,以提高算法的求解效率和效果;為了驗證改進遺傳算法的效果,采用Brute Force算法進行對比計算。 改進操縱方法中的2個決策變量分別是牽引終止位置xcr和初次惰行的起始位置xco,由于二者都是連續(xù)變量,所以在遺傳算法中采用格雷碼編碼。這種編碼技術(shù)有利于提高遺傳算法的搜索能力,避免傳統(tǒng)二進制編碼可能出現(xiàn)的海明(Hamming)懸崖和難以收斂的問題[12]。此外,在遺傳算法的基礎上加入了鄰域搜索模塊,對種群中每個個體的鄰域進行搜索,遺傳算法的求解流程如圖2所示。 由圖2可見:初始種群為隨機產(chǎn)生,種群中的各個個體由一串基于格雷碼編碼的染色體表示,每條染色體包含2個部分,分別對應2個決策變量。在獲得初始種群后,對每個個體進行鄰域搜索,搜索規(guī)則為保持每條染色體的第一部分不變,對第二部分進行變換。即在保持牽引不變的情況下,嘗試不同的初次惰行起始位置。在個體評價模塊中,取目標函數(shù)(1)的倒數(shù)為適應度值,從而將牽引能耗最小化問題轉(zhuǎn)化為最大化問題。對于不滿足區(qū)間運行時分約束但牽引末速度和惰行位置在可行域內(nèi)的個體賦予較小的適應度值,為 圖2 列車節(jié)能操縱方法的遺傳算法求解流程圖 (7) 式中:P(i,j)為算法種群中第i個個體的第j個鄰域解的適應度值;E為牽引能耗;Δt為實際運行時分與給定運行時分之差。 對種群各個體的鄰域進行搜索得到一組局部最優(yōu)解集后更新全局最優(yōu)解。然后,對局部最優(yōu)解集對應的操縱方案進行遺傳交叉、變異操作,更新后的種群進入下一次鄰域搜索,直到達到最大迭代次數(shù)并輸出最優(yōu)解。 Brute Force是一種暴力算法,其主要特點是沒有預處理過程,能夠搜索所有的可行解來獲得精確解。該方法被成功應用于列車節(jié)能操縱問題的求解[13-14]。 改進操縱方法中的決策變量c包括牽引終止位置和初次惰行起始位置,其解空間為χ。Brute Force算法通過遍歷所有的c∈χ并計算能耗,以保證獲得全局最優(yōu)優(yōu)解,計算流程如圖3所示。 圖3 Brute Force算法流程圖 選取北京地鐵5號線和亦莊線中的2個長大下坡區(qū)間進行案例分析,線路參數(shù)如圖4所示,運行列車的基本參數(shù)見表1。遺傳算法中初始種群為30個,交叉概率為0.8,變異概率為0.1,最大迭代次數(shù)為80次。 表1 列車基本特性參數(shù) 圖4 實際運行區(qū)間的坡長和坡度值 列車區(qū)間運行時分取為最小運行時分的1.1倍,其中各區(qū)間的最小運行時分可以通過最大牽引、巡航和最大制動的節(jié)時操縱方案獲得。使用Brute Force算法分別求解給定運行時分下的操縱方案和能耗水平,結(jié)果見表2。 表2 標準四階段操縱方法和改進操縱方法能耗對比 由表2可知:在不考慮再生制動能利用的情況下,采用改進操縱方法在區(qū)間一可以取得較好的節(jié)能效果,節(jié)能率達34.22%。如果考慮再生制動利用,根據(jù)既有文獻[15]可知再生制動能的利用率一般不超過2/3,則采用改進操縱方法在區(qū)間一的可以在再生能減少量不超過2.05 kW·h(3.08 kW·h的2/3)的前提下仍可節(jié)約牽引能耗,依然可以實現(xiàn)節(jié)能。 為進一步說明改進操縱方法節(jié)能的原理,列車在區(qū)間一內(nèi)采用2種操縱方法對應的速度位移曲線的對比如圖5所示。由圖5可見:改進操縱方法將惰行位置提前,可以較好地利用長大下坡為列車加速,在達到限速后轉(zhuǎn)入巡航,從而減少了加速階段的牽引工況時長、增加了惰行工況比例,實現(xiàn)了列車牽引節(jié)能。 圖5 標準四階段和改進操縱方法在區(qū)間一的速度曲線對比(富余時分比例10%) 雖然改進操縱方法在區(qū)間一內(nèi)獲得了較好的節(jié)能效果,但是2種操縱方法在區(qū)間二的能耗相同。這說明改進操縱方法的節(jié)能效果與區(qū)間內(nèi)的坡道情況有關。此外,理論分析可以得知改進操縱方法的能耗表現(xiàn)還與運行時分和線路限速有關。為了研究運行時分和限速對改進操縱方法節(jié)能效果的影響,計算不同富余時分比例下改進操縱方法在不同坡道上(2個區(qū)間)的節(jié)能率,并分別取線路限速為70,80和90 km·h-1,計算結(jié)果如圖6和圖7所示。 圖6 節(jié)能率隨富余運行時間變化趨勢圖 圖7 標準四階段和改進操縱方法在區(qū)間二的速度曲線對比(富余時分比例4%) 當限速為80或90 km·h-1時,節(jié)能率呈現(xiàn)先增加后減少的變化趨勢,最后與標準四階段法的能耗相同。富余時分比例為4%時2種操縱方法下的列車速度位移曲線如圖7所示。由圖7可見:改進操縱方法采用2次惰行和2次巡航,相比標準四階段可以更加充分地利用坡道勢能為列車提速,從而減少牽引工況的持續(xù)時間,實現(xiàn)節(jié)能;但隨著富余時分的持續(xù)增加,標準四階段法中惰行工況所占的比例將增加,因此改進操縱方法的節(jié)能效果逐漸減小;富余時分增加到一定程度后2種操縱方法所得列車速度位移曲線會重合,其牽引能耗也相同。 當限速為70 km·h-1時,改進操縱方法總是能獲得更加節(jié)能的操縱方案,這是因為列車即使從起點開始惰行依然會在運行過程中達到限速。以富余時分比例為10%的情況為例,列車運行在區(qū)間一的速度曲線如圖8所示。由圖8可見:由于區(qū)間內(nèi)都是長大下坡且限速較低,即使惰行也會很快達到限速,因此標準四階段法采用牽引至一定速度再巡航較長距離的操縱方式來保證不超限速且滿足運行時分的要求;而改進操縱方法將操縱序列調(diào)整為最大牽引—惰行—巡航—最大制動,在滿足運行時分要求的前提下充分利用坡道勢能,不需長距離牽引,通過提高惰行比例以實現(xiàn)節(jié)能。 圖8限速70 km·h-1情況下不同操縱方法時速度位移曲線(富余時分比例10%) 因為遺傳算法并不能保證獲得最優(yōu)解,所以引入Brute Force算法計算精確解,并對改進遺傳算法的計算結(jié)果進行評價。以限速為80 km·h-1、富余時分比例10%下改進操縱方法在2個區(qū)間的操縱方法為例,不同計算時分下采用改進遺傳算法與采用Brute Force算法獲得的能耗和計算時間見表3。從表3可知:改進遺傳算法經(jīng)過45 s計算就能獲得較優(yōu)解(離精確最優(yōu)解僅差6%)。 表3改進遺傳算法與BruteForce算法的求解對比(富余時分比例) 運行區(qū)間采用BruteForce算法時能耗/(kW·h)計算時間/s采用改進遺傳算法時不同計算時間下的能耗/(kW·h)15s30s45s區(qū)間一59410863690645623區(qū)間二5759658662640605 區(qū)間一在上述條件下使用改進遺傳算法求解的適應度變化趨勢如圖9所示。由圖9可見:種群隨著迭代次數(shù)的增加逐漸收斂。 圖9 遺傳算法適應度變化趨勢 (1) 針對標準四階段法在含有長大下坡區(qū)間不能充分利用坡道勢能的問題對其進行改進,在不改變四階段操縱工況組成的前提下對工況的序列進行優(yōu)化,盡可能減少運行途中制動工況的出現(xiàn)。 (2) 使用實際線路和車輛參數(shù)對標準四階段和本文改進操縱方法在不同坡道、不同限速、不同運行時分下的列車運行能耗進行了對比分析。結(jié)果表明,在部分長大下坡道區(qū)間,本文方法比傳統(tǒng)四階段方法可以節(jié)能30%以上;本文方法的節(jié)能效果隨著富余時分的增加呈現(xiàn)先增加后減小的變化趨勢,隨著限速的降低而增加。 (3) 分別采用改進遺傳算法和Brute Force算法對改進操縱模型進行求解,結(jié)果表明改進遺傳算法可以在45 s內(nèi)獲得較優(yōu)解,且該解與Brute Force算法求到的精確最優(yōu)解差異約為6%。 (4) 本文尚未考慮列車區(qū)間限速的變化,含長大下坡的變限速區(qū)間的改進操縱方法還有待進一步研究。 [1]FIGUERA J. Automatic Optimal Control of Trains with Frequent Stops[J]. Dyna, 1970, 45(7): 263-269. [2]LEE G H,MILROY I P,TYLER K. Application of Pontryagin’s Maximum Principle to the Semi-Automatic Control of Rail Vehicles [C]// Proceedings of Second Conference on Control Engineering. Newcastle: Institution of Engineers, Australia, 1982: 233-236. [3]ASNIS I A,DMITRUK A V,OSMOLOVSKII N P. Solution of the Problem of the Energetically Optimal Control of the Motion of a Train by the Maximum Principle [J]. USSR Computational Mathematics and Mathematical Physics, 1985, 25(6): 37-44. [4]HOWLETT P G. An Optimal Strategy for the Control of a Train [J]. Journal of the Australian Mathematical Society, 1990, 31(4):454-471. [5]王青元, 馮曉云. 列車準點節(jié)能運行的控制工況最優(yōu)切換研究[J]. 中國鐵道科學, 2016, 37(2):91-98. (WANG Qingyuan, FENG Xiaoyun.Optimal Switching for Control Conditions of Punctual and Energy Efficient Operation of Train[J]. China Railway Science, 2016, 37(2):91-98. in Chinese) [6]荀徑, 唐濤, 宋曉美,等. 再生制動條件下的城軌列車節(jié)能駕駛綜合模型[J]. 中國鐵道科學, 2015, 36(1):104-110. (XUN JING, TANG Tao, SONG Xiaomei, et al. Comprehensive Model for Energy-Saving Train operation of Urban Mass Transit under Regenerative Brake [J]. China Railway Science, 2015, 36 (1): 104-110. in Chinese) [7]丁勇,劉海東,柏赟,等. 地鐵列車節(jié)能運行的兩階段優(yōu)化模型算法研究[J]. 交通運輸系統(tǒng)工程與信息,2011,11(1):96-101. (DING Yong, LIU Haidong, BAI Yun, et al. A Two-Level Optimization Model and Algorithm for Energy-Efficient Urban Train Operation [J]. Transportation Systems Engineering and Information, 2011, 11 (1): 96-101. in Chinese) [8]牟瑞芳, 肖琴杰. 基于速度集的高速動車組運行能耗優(yōu)化操縱模型及算法[J]. 中國鐵道科學, 2014, 35(3):107-112. (MOU Ruifang, XIAO Qinjie. Optimized Control Model and Algorithm Based on Speed Set for Operation Energy Consumption of High Speed EMU [J]. China Railway Science, 2014, 35 (3): 107-112. in Chinese) [9]楊杰, 賈利民, 盧少鋒,等. 電力牽引貨運列車節(jié)能運行研究(一):目標速度曲線優(yōu)化[J]. 鐵道學報, 2016, 38(4):22-31. (YANG Jie, JIA Limin, LU Shaofeng. Energy-Efficient Operation of Electric Freight Trains-Part Ⅰ:Speed Profile Optimization [J]. Journal of the China Railway Society, 2016, 38(4): 22-31. in Chinese) [10]張守帥, 田長海. 高速鐵路長大下坡地段列車運行速度相關問題研究[J]. 中國鐵道科學, 2017, 38(3):124-129. (ZHANG Shoushuai, TIAN Changhai. Study on Related Problems of Train Operation Speed on Long Heavy down Grade of High Speed Railway [J]. China Railway Science, 2017, 38 (3): 124-129. in Chinese) [11]HOWLETT P G,PUDNEY P J,VU X. Local Energy Minimization in Optimal Train Control[J]. Automatica, 2009, 45(11): 2692-2698. [12]SCHRAUDOLPH N N,BELEW R K. Dynamic Parameter Encoding for Genetic Algorithms[J]. Machine Learning, 1992, 9(1):9-21. [13]ZHAO N,ROBERTS C,HILLMANSEN S,et al. An Integrated Metro Operation Optimization to Minimize Energy Consumption [J]. Transportation Research Part C: Emerging Technologies, 2017, 75: 168-182. [14]FAN B,ROBERTS C,WESTON P. A Comparison of Algorithms for Minimising Delay Costs in Disturbed Railway Traffic Scenario [J]. Journal of Rail Transport Planning & Management, 2012, 2: 23-33.3 模型求解
3.1 改進遺傳算法
3.2 Brute Force算法
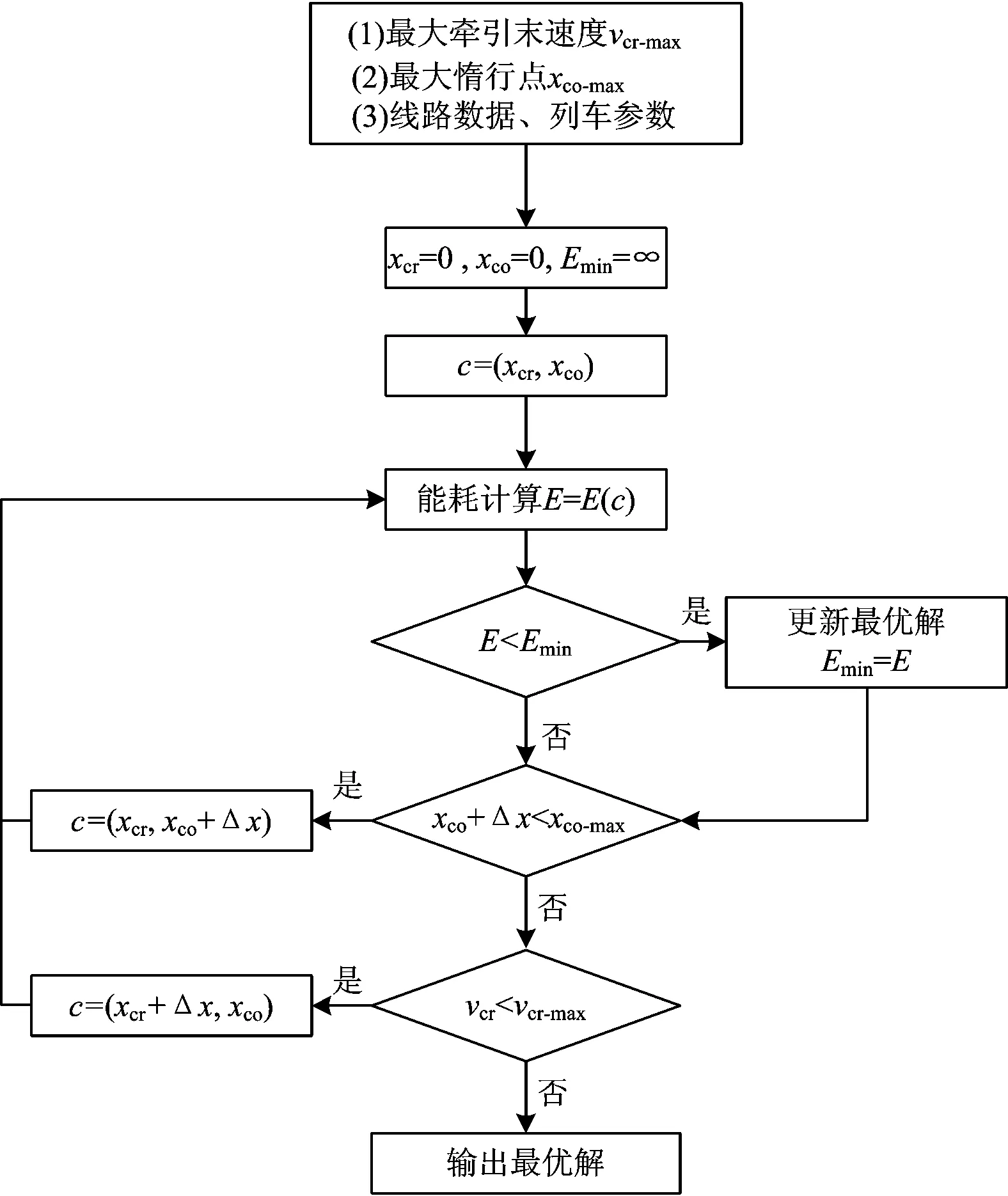
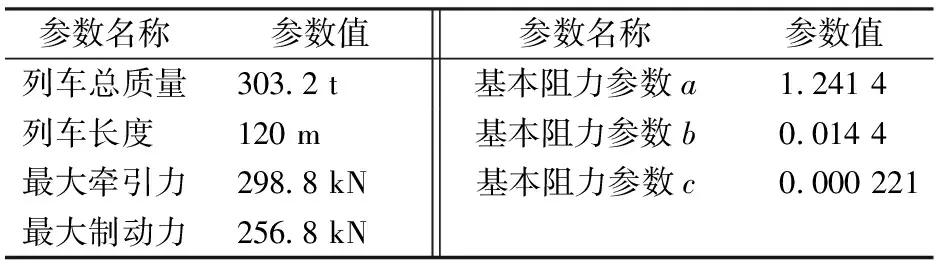
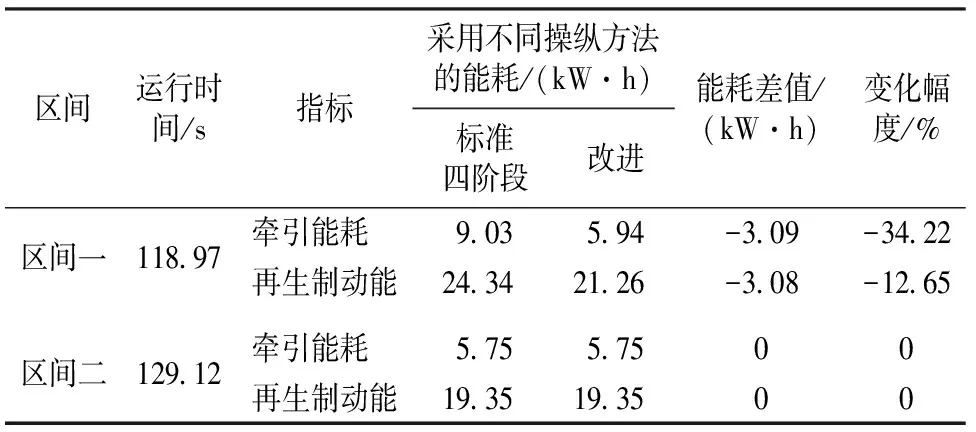
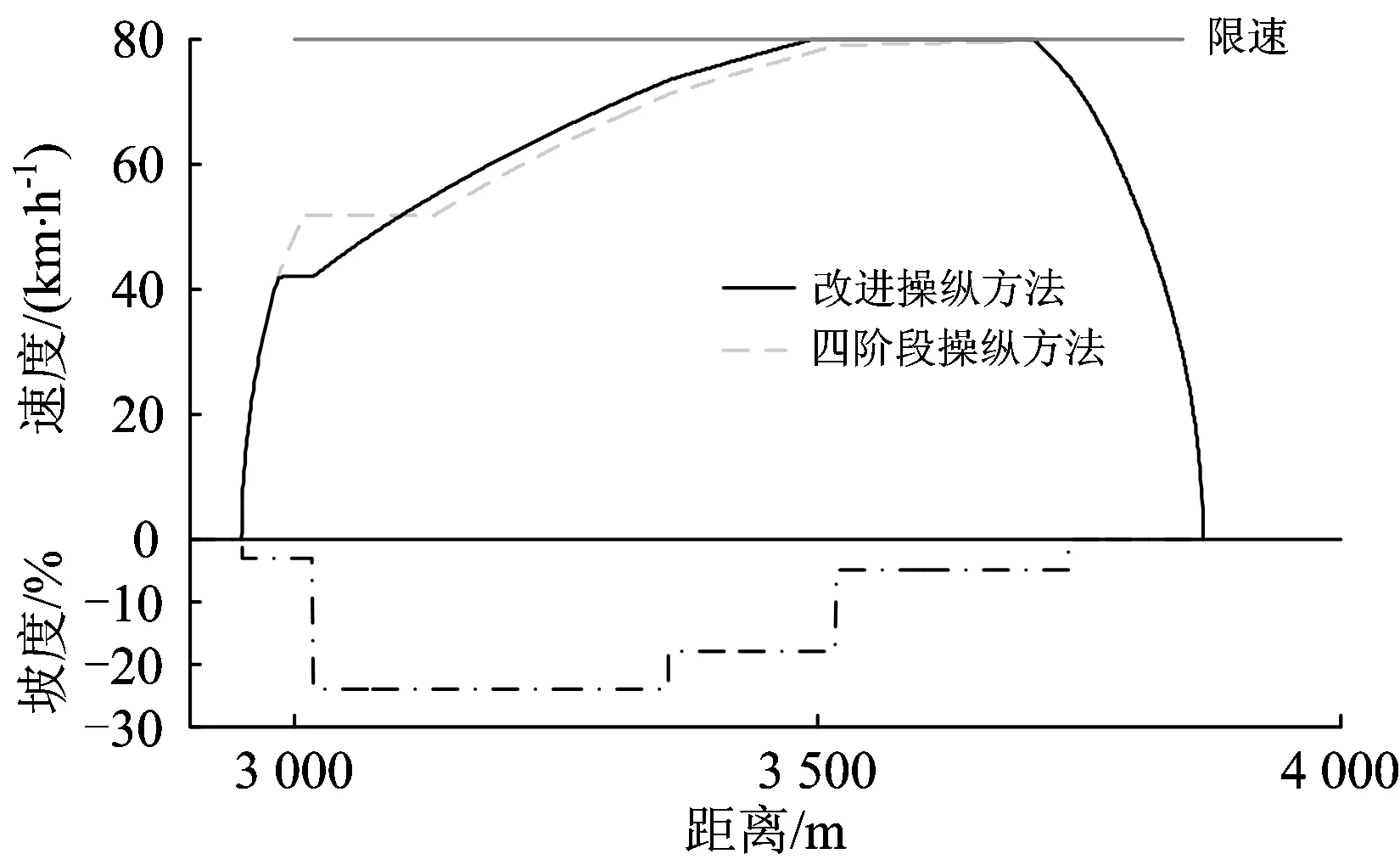
4 案例分析

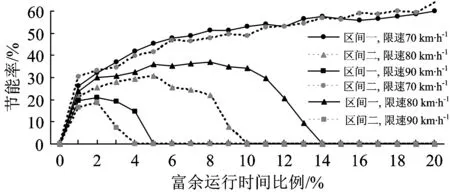
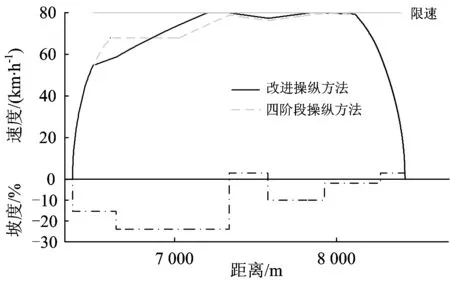
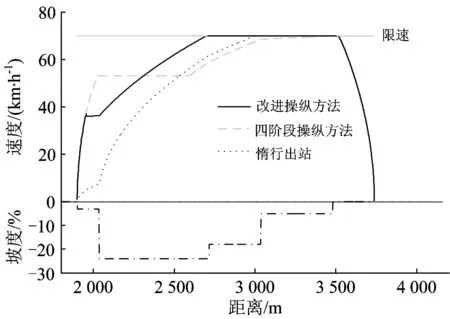
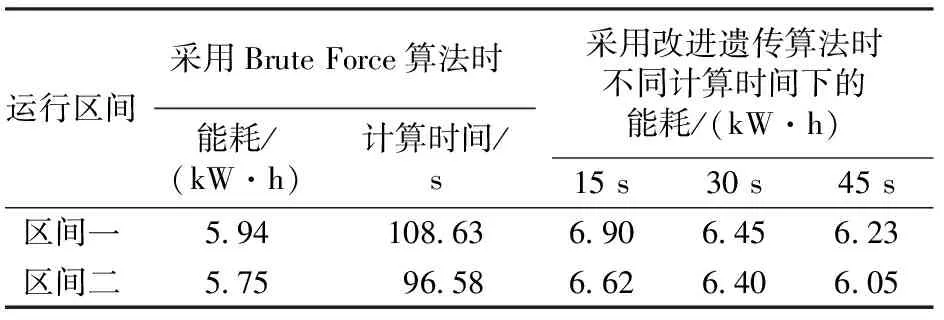
5 結(jié) 論

