基于概率模型的高速鐵路地震預警實時性與準確性分析
王 瀾,戴賢春,習年生,魏 猛
(中國鐵道科學研究院 鐵道科學技術研究發展中心,北京 100081)
高速鐵路地震預警,是根據地震監測臺站實時測定的地震P波初至信息快速估算的地震動參數,確定地震影響區域及其警報等級,在破壞性地震波到達之前,向地震影響范圍內的鐵路系統發布地震緊急處置信息,聯動觸發相關系統對運行列車采取減速或緊急制動。有效的高速鐵路地震預警及緊急處置措施可使列車在地震災害發生時的損失程度降至最小[1]。隨著我國大范圍高速鐵路的開通運營,地震危害的潛在風險越來越突顯,對地震預警系統的實時性與準確性要求也越來越高[2-3]。
國外學者早將地震視為隨機事件,將概率論與數理統計方法用于地震預警中。Iunio等[4]提出基于概率模型發布警報的決策規則:若實時預測分析的地震動加速度峰值大于給定警報閾值的概率超過某一臨界概率值時則發布警報。Andrew和Richard[5]采用統計學方法預測地震震源位置。Vladimir[6]基于概率模型證明了地震預警有效性隨震中距和震級的不同而相應變化。Richard等[7]采用地震P波初至到系統發出預警信息的時延描述地震預警實時性,并基于概率模型進行了地震預警實時性分析。Huseyin等[8]采用統計學方法對地震監測臺站密度進行了優化,進一步提高了地震預警的準確性。Simona等[9]和Aldo等[10]基于統計學方法系統研究了地震事件識別、地震要素估計和地震預警方法,研發的基于概率模型的地震預警系統(PRESTo)得到成功應用。Nakamura等[11]基于統計學方法實時估計地震要素,研發的緊急地震檢測報警系統(UrEDAS)提高了日本新干線抗震減災能力。Iunio等[12]建立了基于概率模型的地震漏報與地震誤報數學模型,并用此評價地震預警的準確性。由此可見,概率論與數理統計方法是研究地震預警實時性與準確性的基礎。
本文結合我國高速鐵路技術特點與實際需求,建立數學概率模型,研究高速鐵路地震預警實時性與準確性的分布特征和參數,通過實時性與準確性綜合分析,提出高速鐵路地震預警發布決策方法。
1 地震預警實時性和準確性模型
地震預警的實時性是指地震預警信息發出時刻相對于震中地震發生時刻的實時程度。本文采用首臺站地震P波初至到系統發出預警信息的時延(簡稱為地震預警時延)進行評價,該時延越小,實時性越好。
地震預警的準確性是指震源定位、震級估算和地震發生時刻推算的準確程度;本文采用震源定位偏差進行評價,該偏差越小,準確性越好。
1.1 地震預警實時性常規概率分布模型
地震預警時延包括:信號濾波時延、數據采集時延、數據打包時延、數據處理時延、預警決策分析時延、數據發送時延、信息排隊與傳輸時延等。受地理構造、地質條件、環境等不確定性因素影響,在不同的預警方式、數據采集處理、警報發布決策、數據傳輸條件下,地震預警時延具有較強的不確定性、離散性和隨機性。實測數據表明,高速鐵路地震預警時延具有單邊、連續性、非對稱型隨機變量分布特征和統計規律性。
針對上述特征,地震預警時延可采用隨機變量進行描述。常規的概率分布模型包括正態分布、對數正態分布、伽馬分布模型等。
正態分布的概率密度函數、數學期望和方差分別為
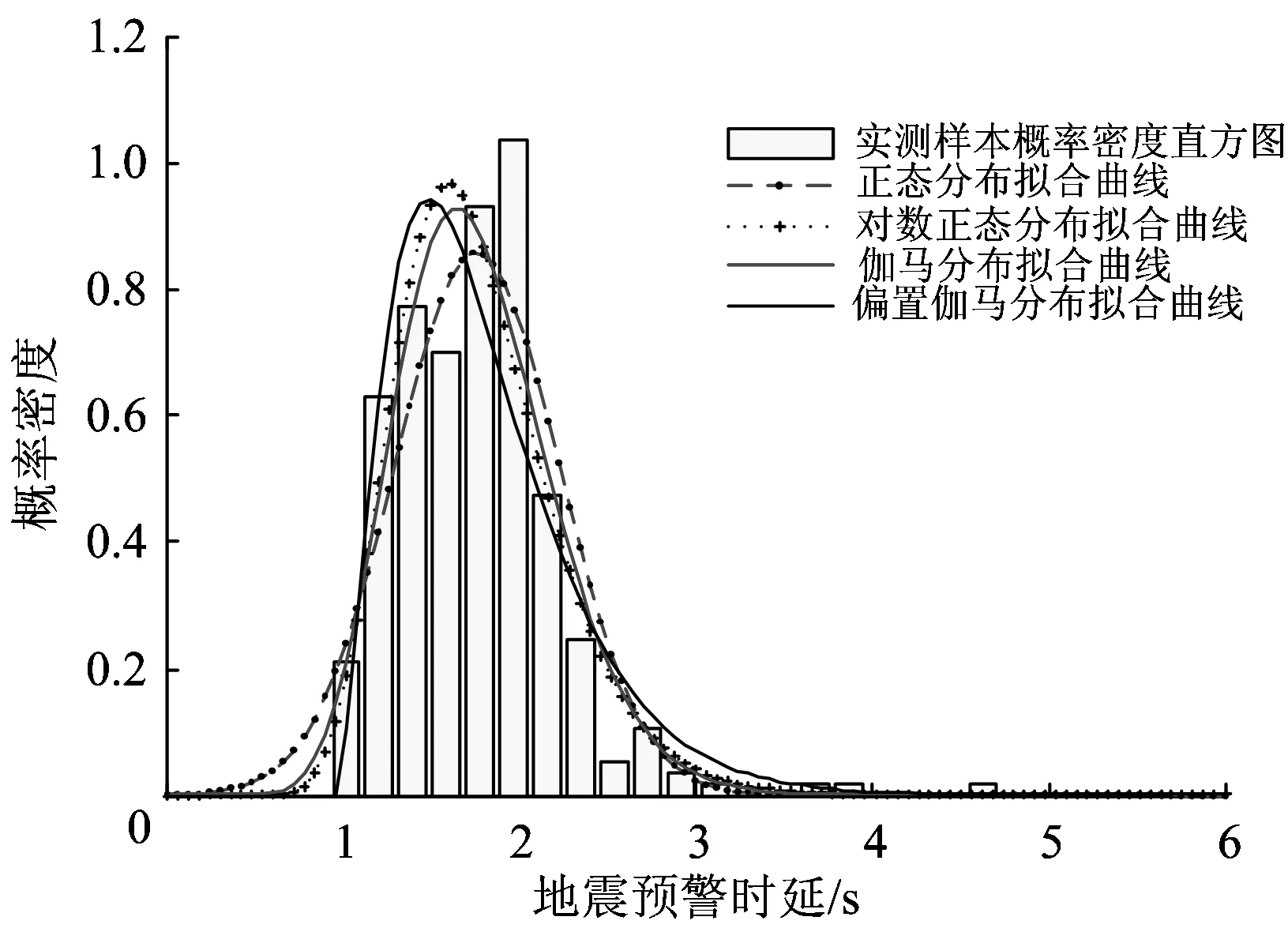
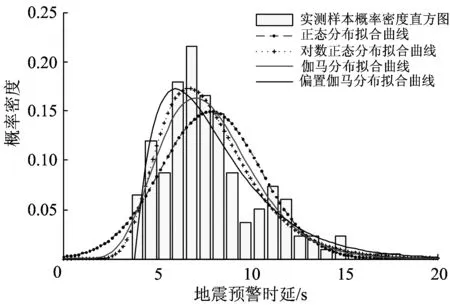
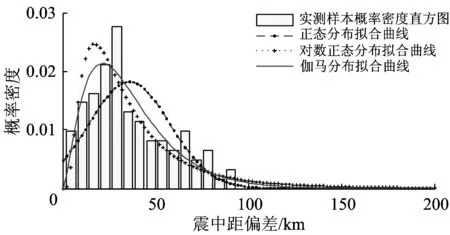
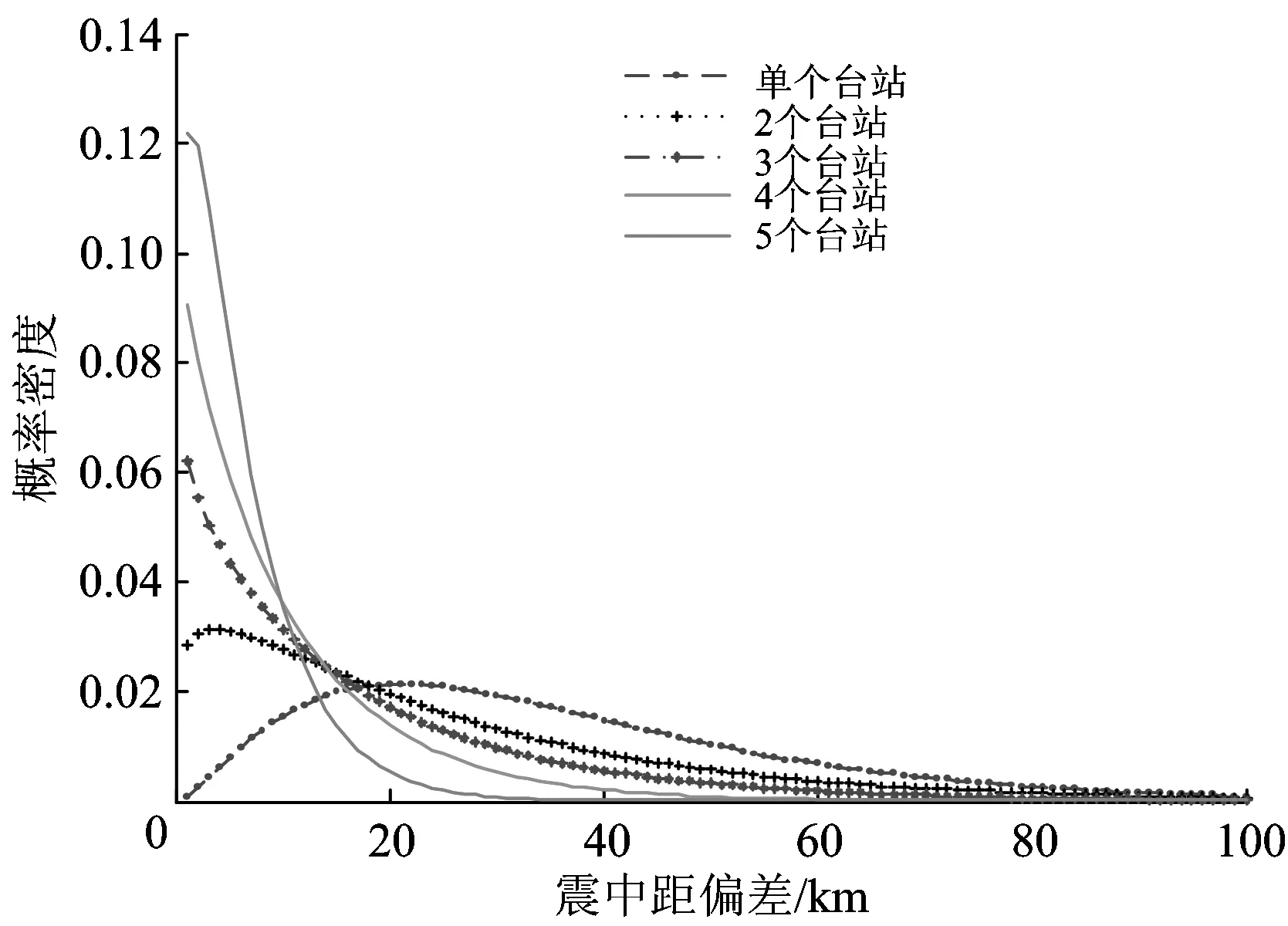
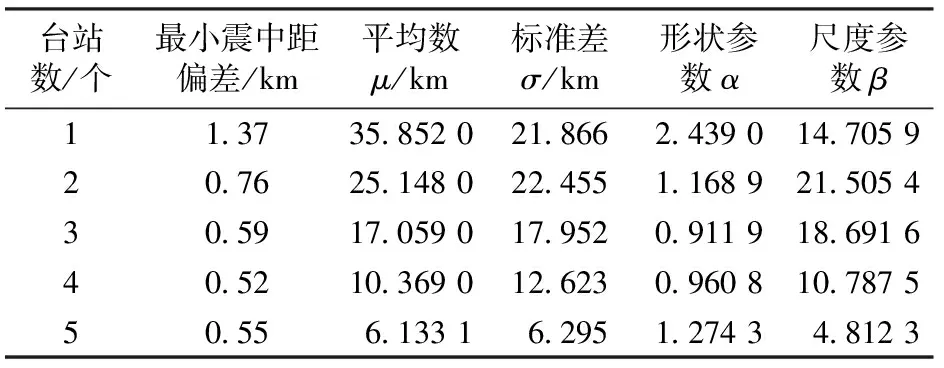
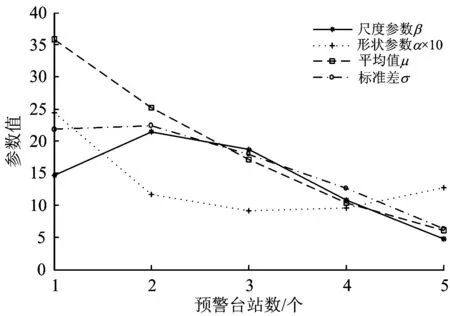
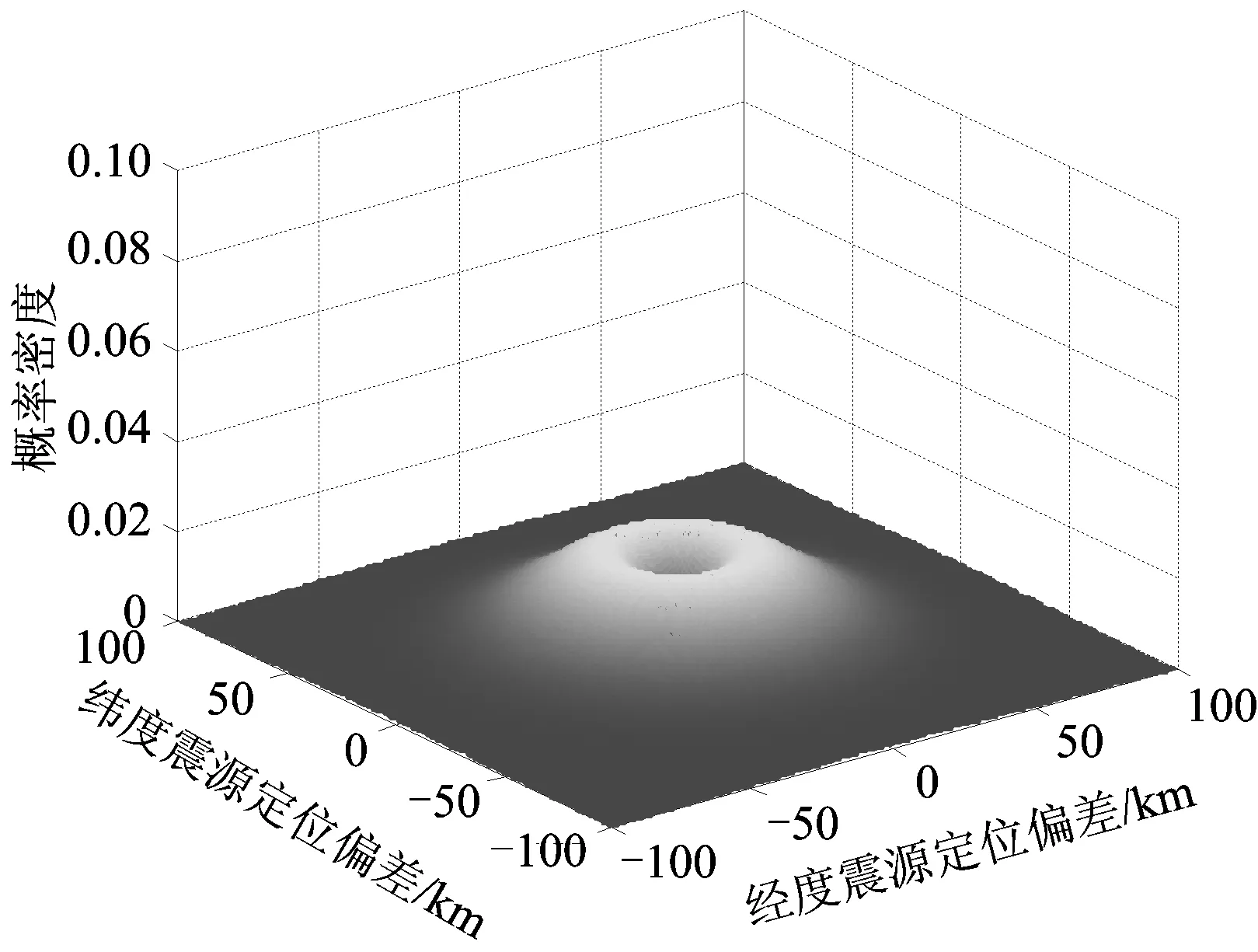
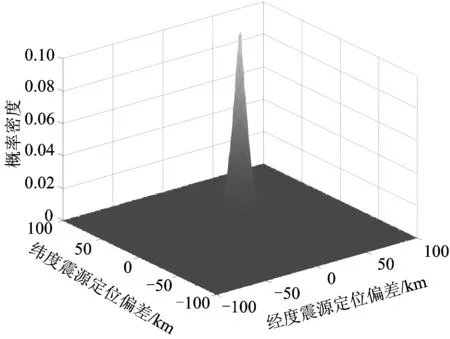
-∞ (1) E(X)=μ D(X)=σ2 式中:y為概率密度函數;X為隨機變量;x為隨機變量取值;μ為平均數;σ為標準差。 對數正態分布的概率密度函數、數學期望和方差分別為 0 (2) D(X)=(eσ2-1)e2μ+σ2 伽馬分布的概率密度函數、數學期望和方差分別為 (3) E(X)=αβ D(X)=αβ2 式中:α為形狀參數;β為尺度參數;Γ(α)為Gamma函數。 (4) 1.2.1偏置伽馬分布模型的建立 實際上,信號濾波、數據采集、數據打包、數據處理、信息傳輸等時延均可視為由隨機時延和固定時延兩部分組成。隨機時延由系統自然規律所決定,具有不確定性、離散性和隨機性;而固定時延相當于接近常量的值,具有確定性和相對性。固定時延無法避免,也就是說,地震預警時延不會小于1個最小值,在這一最小值時間內生成預警信息的可能性不存在。因而,采用正態分布、對數正態分布或伽馬分布等概率密度函數描述地震預警時延,均存在小概率情況下無法正確評價地震預警特征的問題。 鑒于此,為更精確地描述地震預警時延的特征,提出1種地震預警時延精確概率分布——偏置伽馬分布。偏置伽馬分布函數的特點是在常規的伽馬分布函數基礎上增加了1個偏置量,用于描述固定時延。偏置伽馬分布的概率密度函數為 T=f(t|α,β) (5) 即T服從偏置伽馬分布,記為 T~Γ0(α,β,C)t>C (6) 式中:T為時延隨機變量;t為時延隨機變量取值;C為偏置量,且C≥0,當樣本數量足夠大時,可以用樣本最小值作為C的估計值;Γ0為偏置伽馬函數,即 (7) 偏置伽馬分布的數學期望和方差分別為 (8) (9) 特征函數為 Ψ(t-C)=[1-iβ(t-C)]-α (10) 1.2.2偏置伽馬分布的性質 命題,設T~Γ0(α,β,C),則有 T-C~Γ(α,β) (11) 證明:將t-C=x代入式(3),由于x>0,則t>C,由此可得到式(5),從而可知T-C~Γ(α,β),即T-C服從伽馬分布。 由此可知:偏置伽馬分布是一種廣義的伽馬分布,當偏置量C=0時,偏置伽馬分布即是伽馬分布。因而,偏置伽馬分布具有伽馬分布的所有性質,是一種非對稱、連續型分布。 1.2.3偏置伽馬分布參數的極大似然估計 偏置伽馬分布參數的極大似然估計方法如下:設ti是來自總體的樣本,對于ti>C,將式(5)取似然函數可得 (12) 對式(12)兩端取對數,得對數似然函數為 (13) 其一階條件為 (14) (15) 由式(15)得到 [lnΓ0(α)]′ (16) 即 (17) 由此得出 (18) 即 (19) 綜合式(15)和式(17)可得 (20) (21) 震源定位參數包括震中距、方位角、震源深度等。為簡化起見,本文僅以震中距偏差和方位角偏差作為震源定位偏差,用于評價地震預警的準確性。根據震中距偏差的分布特征,設其服從伽馬分布;方位角偏差取決于臺站與震中的相對位置、預警臺站數、計算方法等因素,當樣本足夠大時,宏觀上可以認為其服從均勻分布。因此,以震中距偏差和方位角偏差作為二維隨機變量,則震源定位偏差的服維概率密度函數為 (22) 其中,震中距偏差的概率密度函數為 (23) 式中:X為震中距偏差隨機變量;x為震中距偏差隨機變量取值;θ為方位角偏差隨機變量。 采用新研發的某高速鐵路地震預警系統進行地震預警性能試驗。輸入的地震波包括國內和日本天然地震記錄數據共300條,其震中距分別為0~50,50~100和100 km以上;試驗中將地震監測臺站坐標按照各采集數據臺站的實際經緯度進行動態設置,將天然地震記錄數據按照各采集數據臺站的實際時差進行回放;時延測試前利用GPS時間校準;地震監測臺站數分別選取1,2,…,5個。 分別用正態分布、對數正態分布、伽馬分布、偏置伽馬分布函數對試驗中測試的地震預警時延進行擬合對比,結果如圖1和圖2所示。由圖1和圖2可以看出:單臺站與多臺站地震預警時延均可以采用本文提出的偏置伽馬分布概率密度函數進行擬合;偏置伽馬分布概率密度函數可有效地描述地震預警時延的偏置量、非正態形狀以及分布特征。經顯著性檢驗,表明地震預警時延服從本文提出的偏置伽馬分布,記為 圖1 單臺站地震預警時延概率密度函數擬合 TEEW=Γ0(α,β,C) (24) 圖2 5個臺站地震預警時延概率密度函數擬合 分別用正態分布、對數正態分布、伽馬分布函數對試驗中測試的地震預警震中距偏差進行擬合對比,結果如圖3和圖4所示。 圖3 單臺站地震預警震中距偏差概率密度函數擬合 圖4 5個臺站地震預警震中距偏差概率密度函數擬合 可以看出,采用伽馬分布概率密度函數描述地震預警震中距偏差,與其他類型的分布函數相比,可以更有效地描述其單邊性、連續性、非對稱型的分布特征。經顯著性檢驗,表明地震預警震中距偏差服從伽馬分布,記為 XEEW~Γ(α,β) (25) 不同臺站數量時,從首臺站P波初至到地震預警監測鐵路局中心系統發出地震預警信息,地震預警時延的偏置伽馬分布概率密度對比如圖5所示,時延統計值及偏置伽馬分布概率密度函數參數的極大似然估計值見表1,時延統計值及偏置伽馬分布概率密度函數參數變化規律如圖6所示。 圖5不同臺站數量時地震預警時延的偏置伽馬分布概率密度比較 表1 不同臺站數量時地震預警時延統計值及偏置伽馬分布參數估計值 圖6不同臺站數量時地震預警時延統計值及偏置伽馬分布參數的變化規律 由圖5、圖6和表1不難看出:地震預警的實時性隨著預警臺站數的增加而下降;描述固定時延的偏置量C隨著預警臺站數的增加而明顯增加,描述隨機時延的平均數μ和標準差σ均成對數關系增長;偏置伽馬分布概率密度函數的形狀參數α與臺站數無顯著對應變化規律;尺度參數β與臺站數對應關系密切,雙臺站比單臺站的明顯增加,此后隨著預警臺站數的增加而緩慢增加。 不同臺站數量時地震預警震中距偏差偏置伽馬分布概率密度對比如圖7所示,震中距偏差統計值及偏置伽馬分布概率密度函數參數的極大似然估計值見表2,震中距偏差偏置伽馬分布概率密度函數參數變化規律如圖8所示。 圖7不同臺站數量時地震預警震中距偏差的偏置伽馬分布概率密度比較 表2不同臺站數量時地震預警震中距偏差的統計值及偏置伽馬分布參數估計值 臺站數/個最小震中距偏差/km平均數μ/km標準差σ/km形狀參數α尺度參數β1137358520218662439014705920762514802245511689215054305917059017952091191869164052103690126230960810787550556133162951274348123 圖8不同臺站數量時地震預警震中距偏差的統計值及偏置伽馬分布參數變化規律 由圖7、圖8和表2不難看出:地震預警準確性隨著臺站數的增加明顯提高;地震預警震中距偏差隨著臺站數的增加明顯降低,平均值μ和標準差σ明顯減小并快速收斂;偏置伽馬分布概率密度函數形狀參數α呈凹狀曲線,尺度參數β呈凸狀曲線。 依據表2給出的地震預警震中距偏差偏置伽馬分布參數估計值,采用式(21)并經坐標變換后可得出震源定位偏差的二維概率密度函數,其中單臺站與5個臺站地震預警震源定位偏差的二維概率密度如圖9和圖10所示。 圖9 單臺站地震預警震源定位偏差二維概率密度 圖10 5個臺站地震預警震源定位偏差二維概率密度 由圖9和圖10可以看出:單臺站地震預警震源定位偏差分布較為分散,并未向震源中心凝聚;隨著預警臺站數的增加,地震預警震源定位偏差快速減小,其偏差分布向震源中心凝聚,并由寬變窄,震源定位準確性明顯提高。 由于地震事件、地質構造等的不確定性,地震預警的實時性與準確性是一對相互矛盾的性能參數。若過于強調實時性則必定會降低準確性,若提高準確性則一定會降低實時性。同時,準確性的下降又會減少系統的可信度[13]。 在實際工程應用中,地震預警的實時性和準確性的取舍還與采取地震緊急處置措施所付出的代價有關[13],三者的關系如圖11所示。是否實時采取地震緊急處置措施,取決于緊急處置措施的影響程度和采取緊急處置措施所付出的代價。如果采取地震緊急處置措施的代價昂貴,則不必過于強調地震緊急處置的實時性,如生命線工程的停機可能代價昂貴,那就不得不最大限度地提高地震預警的準確性,以避免因可能發生的地震誤報而采取緊急處置所帶來的經濟損失,但這樣可獲得的預警提前時間十分有限。對于學校而言,地震到來前,盡快讓人員逃離到室外空曠場地躲避是最好的地震應對措施,該措施除造成一定的課時損失外幾乎不必付出任何代價,因而獲取充分的預警提前時間比過于強調預警準確性更為重要。 圖11 地震預警的實時性和準確性與措施代價的關系 對于高速鐵路而言,地震預警的實時性與準確性均很重要。實時性好,可在破壞性地震波到達之前采取有效的制動措施,避免運行的高速列車脫軌或傾覆;準確性好,可減少對正常運輸秩序的影響。鑒于實際上實時性與準確性無法完全兼得,因此在進行地震緊急處置決策時需兼顧地震預警的實時性與準確性。為此,針對目前我國高速鐵路地震預警臺站布設現狀,建議采用3個臺站地震預警的方法。3個臺站地震預警可實現:在70%概率情況下地震預警時延小于7 s;在70%概率情況下震中距偏差小于20 km。 (1)地震預警時延服從偏置伽馬分布。隨著預警臺站數的增加,地震預警的時延增加,即地震預警的實時性相應下降,其中描述固定時延的偏置量C明顯增加,描述隨機時延的平均數μ和標準差σ成對數關系增長。 (2)地震預警震中距偏差服從伽馬分布。隨著預警臺站數的增加,震中距偏差明顯降低,即地震預警的準確性明顯提高,其中平均數μ和標準差σ明顯減小并快速收斂;隨著預警臺站數的增加,震源定位偏差快速減小,其偏差分布向震源中心凝聚,并由寬變窄,震源定位準確性明顯提高。 (3)采用3個臺站地震預警方法可兼顧實時性與準確性,是滿足高速鐵路地震預警需求的有效方法,實時性可達到全系統時延在70%概率情況下小于7 s,準確性可實現在70%概率情況下震中距偏差小于20 km。 [1]孫漢武,王瀾,戴賢春,等. 高速鐵路地震緊急自動處置系統的研究[J]. 中國鐵道科學,2007,28(5):121-127. (SUN Hanwu, WANG Lan, DAI Xianchun, et al. Study on the Earthquake Urgent Automatic Alarm System of High-Speed Railway[J]. China Railway Science, 2007, 28(5):121-127. in Chinese) [2]宋晉東,李山有,馬強.日本新干線地震監測與預警系統[J].世界地震工程,2012, 28(4):1-10. (SONG Jindong,LI Shanyou,MA Qiang. Overview on Earthquake Monitoring and Early Warning System for High-Speed Railway (Shinkansen) in Japan[J]. World Earthquake Engineering, 2012, 28(4): 1-10. in Chinese) [3]馬強. 地震預警技術研究及應用[D]. 哈爾濱: 中國地震局工程力學研究所, 2008. (MA Qiang. Study and Application on Earthquake Early Warning[D]. Harbin:Institute of Engineering Mechanics, China Earthquake Administration, 2008. in Chinese) [4]IUNIO Iervolino, VINCENZO Convertito, MASSIMILIANO Giorgio, et al. Real-Time Risk Analysis for Hybrid Earthquake Early Warning Systems[J]. Journal of Earthquake Engineering, 2006, 10(6):867-885. [5]ANDREW B Lockman, RICHARD M Allen. Single-Station Earthquake Characterization for Early Warning[J]. Bulletin of the Seismological Society of America, 2005, 95(6): 2029-2039. [6]VLADIMIR Pinsky. Modeling Warning Times for the Israel’s Earthquake Early Warning System[J]. Journal of Seismology, 2015, 19(1):121-139. [7]RICHARD MAllen, HOLLY Brown, MARGARET Hellweg, et al. Real-Time Earthquake Detection and Hazard Assessment by ElarmS Across California[J]. Geophysical Research Letters, 2009, 36(5):1-6. [8]H SERDAR Kuyuk, RICHARD M Allen. Optimal Seismic Network Density for Earthquake Early Warning: a Case Study from California[J]. Seismological Research Letters,2013, 84(6): 946-954. [9]SIMONA Colombelli, ANTONIO Emolo, ALDO Zollo. A Duration Magnitude Scale for the Irpinia Seismic Network, Southern Italy[J]. Seismological Research Letters, 2014, 85(1):98-107. [10]ALDO Zollo, SIMONA Colombelli, LUCAElia, et al. An Integrated Regional and on-Site Earthquake Early Warning System for Southern Italy: Concepts, Methodologies and Performances[M]. New York: Early Warning for Geolo-gical Disasters, Advanced Technologies in Earth Sciences,Springer,2014: 117-137. [11]NAKAMURA Yutaka,SAITA Jun. UrEDAS, the Earthquake Warning System:Today and Tomorrow[M]. New York: Earthquake Early Warning Systems, Springer, 2007: 249-281. [12]IUNIO Iervolono, VINCENZO Convertito, MASSIMILIANO Giorgio, et al. The Crywolf Issue in Earthquake EarlyWarning Applications for the Campania Region[M]. New York: Earthquake Early Warning Systems, Springer, 2007: 211-232. [13]IUNIO Iervolino, GAETANO Manfredi, EDOARDO Cosenza. Earthquake Early Warning and Engineering Application Prospects[M].New York: Earthquake Early Warning Systems, Springer, 2007: 233-247.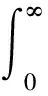
1.2 地震預警實時性精確概率分布模型
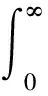
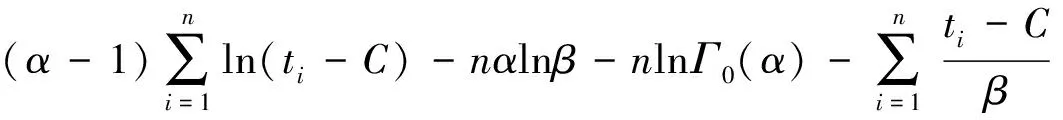
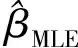
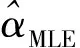

1.3 地震預警準確性概率分布模型
2 模型驗證
2.1 實時性模型驗證
2.2 準確性模型驗證
3 地震預警實時性與準確性
3.1 實時性
3.2 準確性
3.3 綜合分析

4 結 語

