基于自適應環路濾波的相控陣導引頭捷聯解耦方法

蔣兵兵, 盛衛星, 張仁李, 韓玉兵, 馬曉峰

(1. 南京理工大學電子工程與光電技術學院, 江蘇 南京 210094; 2. 上海無線電設備研究所, 上海 200090)

0　引　言

近年來,基于相控陣雷達制導體制[1]的導引頭得到越來越廣泛的應用[2],已成為當今國內外導引頭研制的發展趨勢[3-4]。其具有波束掃描的快速性、抗干擾性能的可靠性等優點[5]。

按照導引頭內測量模塊的安裝位置不同,可以將導引頭分為兩類[6]:隨動式與捷聯式,捷聯式導引頭又可以分為半捷聯與全捷聯形式。半捷聯導引頭仍保留慣性穩定框架結構,并利用彈體自身的慣導系統得到姿態信息[7-9]。相控陣雷達導引頭則屬于全捷聯導引頭[6,10],去除了伺服系統及慣性穩定框架,結構復雜性及成本大大降低,可靠性則得到了提高[10-11]。但其得到的測量信號是相對于導彈本身的,在經典的空空導彈打擊目標的場景下,彈體本身在俯仰、偏航及滾轉方向上存在著嚴重的姿態擾動[4],這樣會影響系統的輸出,引起對目標跟蹤的偏差[12]。因此,必須采用解耦方法來實現波束的穩定,這也成為目前相控陣雷達導引頭研發中的一個重要問題[4,6,12]。

相控陣導引頭的波束穩定方式主要有兩種:速率陀螺穩定與捷聯穩定。這兩類方法的應用都較多[4-5,7-10,13-16],但基本區別在于對信息的獲取和控制方式上。速率陀螺穩定方式是一種直接的硬件穩定方法,而捷聯穩定方式是一種軟件補償方法[16]。速率陀螺穩定利用速率陀螺直接得到姿態角變化,再補償到波束控制系統中。戰術導彈內部空間受限,需移走天線背面的角速率陀螺,簡化封裝并減小體積[16]。天線通過自有的自動駕駛陀螺儀來實現波束的穩定,這種方式稱為捷聯穩定[17]。這樣的系統結構在特定戰斗場景中能保證角度跟蹤環路更好的精度[18]。

針對相控陣導引頭,目前已有的捷聯穩定方法大致可以分為3類[6,19]。第1類方法通過波束調節穩定方式實現解耦,即利用移相器使得導引頭的掃描波束向著彈體姿態運動的反方向偏轉,實現目標在慣性空間的穩定[8,10-11];第2類方法利用捷聯慣導信號進行解耦,由波束指向聯合彈體姿態運動信息,通過相應的坐標系變換得到姿態穩定矩陣,再將所得的補償角疊加到波束指向上,完成對波束指向的修正[4-5,9,15];第3類方法利用現有的濾波算法進行解耦[6,19],如卡爾曼濾波。具體來說,文獻[4]利用波束指向在慣性空間的不變性原理,實時計算波束角,實現了相控陣導引頭波束慣性空間指向穩定的應用要求。文獻[5]在已知天線波束指向以及彈體姿態角的基礎上,利用坐標變換及慣性空間波束指向不變性原理對其做開環補償,同樣實現了波束的解耦。文獻[9]給出一種通過對彈體姿態角速率積分后得到波束角變化率的方法,實現了對波束角的實時修正,從而穩定了波束在慣性空間的指向。文獻[13]創新性地將捷聯解耦算法設計為獨立模塊,在沒有精確初始姿態的情形下,仍然可以得到穩定的波束指向。在文獻[13]所設計的模塊中,為求得天線實時姿態,采用四階龍格—庫塔法對表征彈體姿態的四元數進行更新,再根據信號處理周期內天線波束在空間指向不變的原理,解算得到波束穩定所需的補償角。

文獻[13]中方法是目前解決相控陣雷達導引頭中捷聯解耦問題的優質方案。然而,此方法以及文獻[4-5,9]中方法的性能都依賴于角速度傳感器的測量精度。盡管在小型的雷達導引頭中,應用這些方法可得到滿足工程指標,但在戰術導彈中的導引頭工作時間較長,實際角速度傳感器中受彈體溫度變化等影響,可能會產生超出預期的測量精度惡化及不穩定的零偏問題,由此產生的累積誤差不可忽視。

針對這樣的問題,本文在文獻[13]方法的基礎上,增加了環路濾波器,提出了基于環路濾波的捷聯解耦算法(strapdown decoupling method based on loop filter, SDMLF),使得整個捷聯解耦模塊構成閉環,這樣可以緩解由于彈體姿態角速度測量值不夠準確帶來的不良影響。為進一步提高解耦算法的性能,對環路濾波器中的等效環路噪聲帶寬進行優化,提出了基于自適應環路濾波的捷聯解耦算法(strapdown decoupling method based on adaptive loop filter, SDMALF),使得其可以隨著當前實際的波束指向,自適應地調節,加速波束指向的穩定。

1　捷聯波束穩定原理

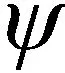
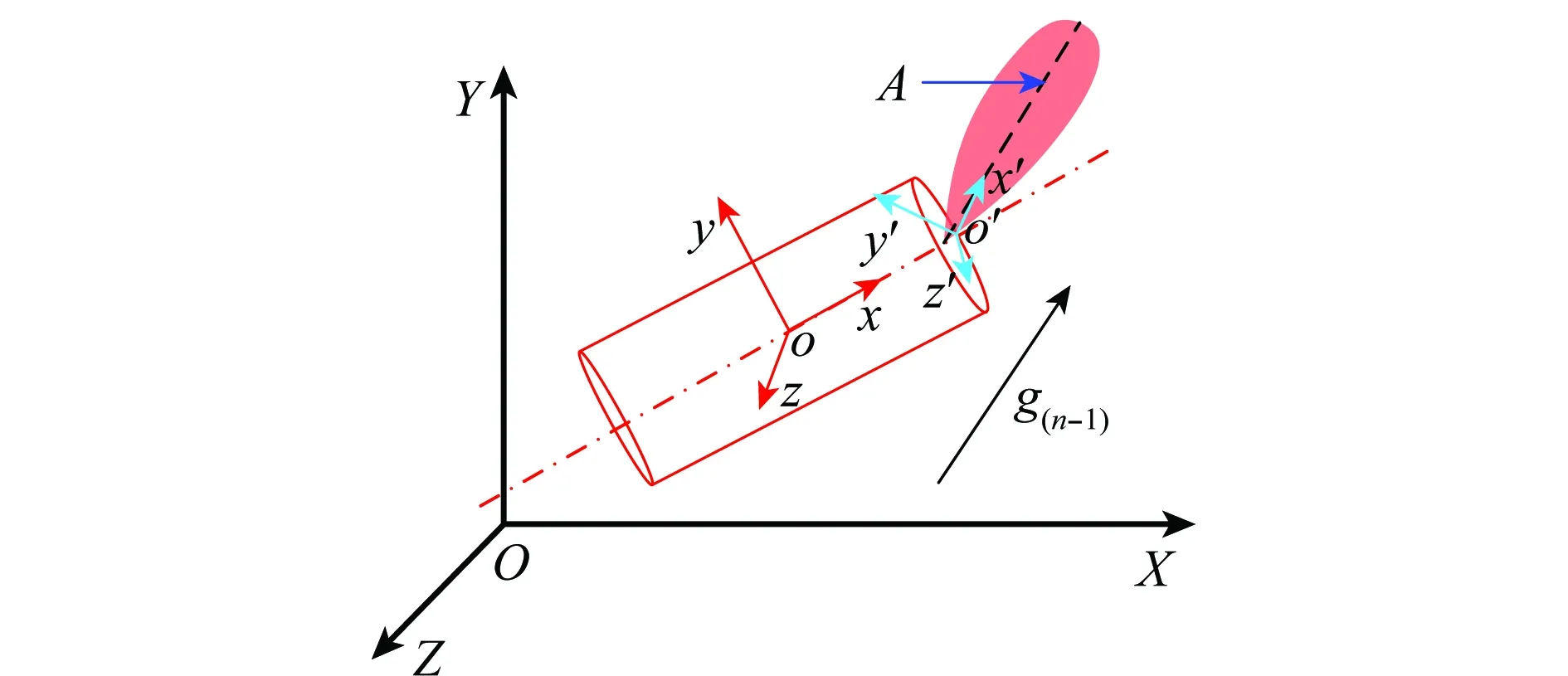
圖1　捷聯解耦算法中坐標系示意圖

文獻[13]中利用慣性空間波束指向不變性原理,得到了波束補償角的計算流程。由四元數表示的坐標系轉換矩陣與姿態角表示的坐標系轉換一致,得到彈體姿態角的計算公式為

(1)

其中,姿態角的四元數表示為

(2)

C23=2(q2q3-q0q1),C31=2(q1q3-q0q2)。

按照式(1)中的姿態角,可得當前時刻的波束指向λy(n)、λz(n),由此得到為維持波束穩定所需的補償角為

(3)

詳盡的步驟可以在文獻[13]中找到,本文后續將文獻[13]中的方法簡記為捷聯解耦算法(strapdown decoupling method, SDM)。

2　SDMLF

環路濾波器是鎖相環的一個重要組成部件,從本質上看,跟蹤載波的鎖相環是一個帶寬非常窄的跟蹤濾波器。近年來,鎖相環已經廣泛地應用在了諸如深空探測通信,電視圖像傳輸,高精度測量和信號檢測中。

鎖相環中包括3個模塊:采樣鑒相器(sampling phase detector, SPD)、環路濾波器(loop filter, LF)與數控振蕩器(digitally controlled oscillator, DCO),其中最重要的就是LF,它是控制整個鎖相環對載波跟蹤快慢以及跟蹤精度的關鍵。SPD得到輸入信號與重建參考信號之間的相位誤差,DCO將LF得到的相位誤差濾波值累加到原有的相位上,如此循環,實現對輸入信號相位的鎖定。

考慮到鎖相環對載波相位跟蹤的高精度性能,本文將其原理推廣到相控陣導引頭解耦算法中。

2.1　SDMLF

典型二階環路濾波器的傳遞函數[20]為

(4)

其中,c1,c2為

(5)

(6)

式中,Kd為環路增益;ξ為衰減因子,通常為0.707;ωn為環路自然角頻率;T為采樣周期。

環路濾波器中最重要的參數就是環路等效噪聲帶寬BL,其很好地反映環路的濾波能力。BL與ξ及ωn之間滿足[20]

(7)

BL取小值時,對輸入信號的跟蹤精度高,但是跟蹤靈敏度較低;BL較大時,環路能夠快速捕捉輸入信號,但跟蹤精度不夠。選取環路噪聲帶寬要盡量減少噪聲引起的相位抖動。

記環路濾波器的輸出為y[n],則環路濾波器的時域差分方程為

y[n]=(c1+c2)·x[n]-c1·x[n-1]+y[n-1]

(8)

式中,x[n]為環路濾波器的輸入。

式(8)中,當前周期的輸入量x[n],上個周期的輸入量x[n-1]、輸出量y[n-1],都體現到了本次的LF輸出y[n]中。LF模塊充分利用了當前時刻之前的所有輸入信息,顯然這對提高環路收斂速度是十分有益的。

圖2為本文的SDMLF算法框圖,其中的初始波束指向為當前捷聯解耦周期所處信號處理周期內由角度跟蹤環路給出的目標指向,初值為系統上電時的波束指向。SDM算法[13]中得到的波束補償角與彈體姿態擾動角大小一致,但仍存在小的誤差。這一特性可類比為鎖相環中的鑒相器,即輸入彈體擾動后的波束指向,經SDM模塊疊加波束補償角后,得到補償后的波束指向,最終此補償后的指向與初始波束指向之間的差值送入LF,此差值反映了SDM模塊對擾動角的鑒別能力。LF得到誤差角的濾波值后,用此值修正當前補償后的波束指向。修正的過程實現了DCO的功能。最后,將更新后的波束指向配置到波控系統中,如此循環,實現閉環控制。

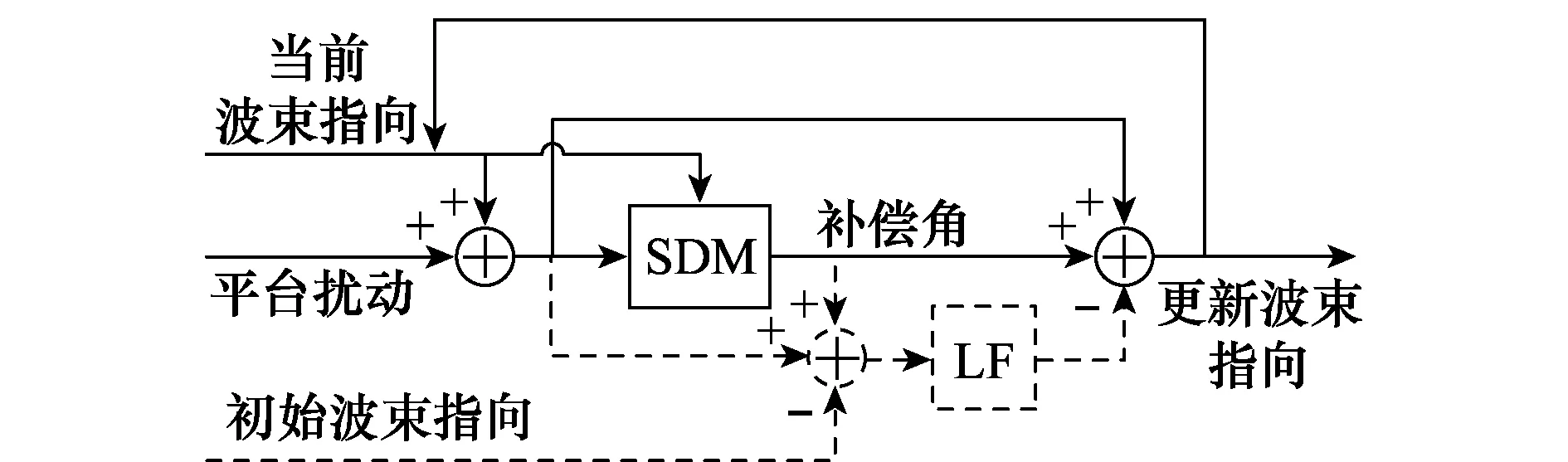
圖2　SDMLF算法框圖

SDMLF算法相比于SDM算法,可以更好地應對角速度傳感器測量值不可靠的情形,但是其中的環路等效噪聲帶寬需要預先初始化,具有局限性。設計BL能夠跟隨整個解耦環路自適應調整的方法才能更好地將其應用到實際工程中。

2.2　SDMALF算法

在SDMLF算法中,環路濾波器的輸入為補償后的波束指向與初始波束指向之間的誤差。在第k個捷聯解耦周期,進入LF模塊前,只有3個信息:當前周期的誤差指向Δ?k,也即第k個解耦周期LF的輸入值;上個周期捷聯解耦環路輸出的波束指向Ψk-1;以及期望的波束指向,也即初始時刻的波束指向Θ0。

從鎖相環的原理出發,若在當前解耦周期所得解耦后的波束指向與初始的波束指向盡可能一致,那么從整個解耦階段看來,這樣的解耦方法就能得到更好的解耦精度。

但在實際情況中,讓Ψk-1與Θ0相等是不可能的。為此,從參數優化角度出發,采用Θ0與Ψk-1差值的平方作為代價函數J，表示為

J=(Θ0-Ψk-1)2

(9)

求解此代價函數取得最小值時對應的環路等效噪聲帶寬,實現LF系數自適應地調整。

(10)

ΔΨ4=(c1+c2)·Δ?4-c1·Δ?3+ΔΨ3=

(c1+c2)·Δ?4-c1·Δ?3+

c1(Δ?3-Δ?1)+c2(Δ?3+Δ?2)+ΔΨ1=

c1(Δ?4-Δ?1)+c2(Δ?4+Δ?3+Δ?2)+ΔΨ1=

(11)

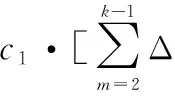
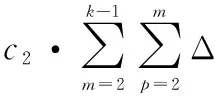
(12)

由此,得到了簡化后的優化問題模型為

J=(c1A1+c2A2+A0)2

其中

(13)

聯立式(5)～式(7),得到

(14)

(15)

其中

(16)

相控陣導引頭的捷聯解耦周期固定,故T為常數,本文中ξ=0.707為常數,故只有一個變量BL。

對J求微分,得

(17)

其中

8A2(1+4ξ2)TBL+A1(1+4ξ2)2

(18)

令dJ/dBL=0,得

(19)

(20)

BL的解中不含A0,因此不用計算A0。

先討論BL的存在性。不考慮A1,A2的正負性,則BL的正負性存在以下4種情況:

(1)BL,1≤0,BL,2≤0;

(2)BL,1≥0,BL,2≤0;

(3)BL,1≥0,BL,2≥0;

(4)BL,1,BL,2為復數。

由于BL須為正,且為使J可取得最小值,則J在其處的二次導數必須為非負數,則

綜上所述,在利用上述流程計算得到BL后,如果BL有解,將其更新為當前解耦周期的環路等效噪聲帶寬;否則,將上個周期的BL更新為當前的等效環路噪聲帶寬。之后再按照圖2的框圖進行處理。

2.3　兩個算法的比較

(1) 本文提出的SDMLF算法相比SDM算法,只多了LF模塊,即增加了式(8)的計算。而此式的計算量可忽略,因此并不影響其在實際工程中的應用。

(2) SDMALF算法相比于SDMLF算法,增加了對BL的自適應計算,但是BL的解析解已在式(19)、式(20)給出,其計算很簡單。因此,SDMALF對實際工程應用同樣具有友好性。

2.4　本文算法應用到角跟蹤系統中

相控陣導引頭中的角跟蹤系統包含解耦模塊與角度跟蹤環路,將本文所提的算法聯合典型的角度跟蹤環路,得到了角跟蹤系統示意圖,如圖3所示。角度跟蹤環路得到的角誤差在每個信號處理幀到來時刻更新,其他時刻置為0。圖3中右下角的信號處理幀標志位在信號處理幀到來時刻為1,其他時刻為0。

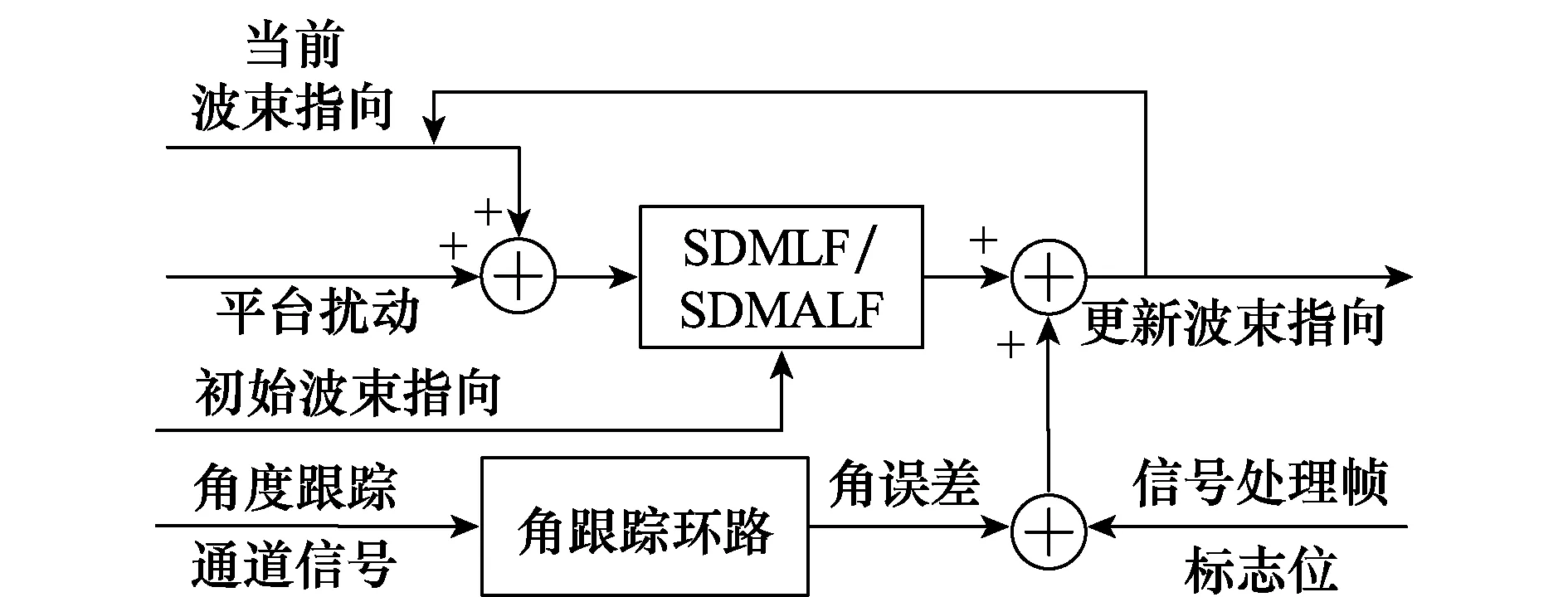
圖3　角跟蹤系統示意圖

在角跟蹤系統中的捷聯解耦周期內,首先利用本文SDMLF或SDMALF算法實現對波束補償角的解算,當信號處理幀未到來時,在每個捷聯解耦周期內,將波束補償角疊加到當前的波束指向上,更新當前的波束指向,維持每個信號處理周期內的波束穩定。在信號處理幀標志位為1時,用角度跟蹤環路得到的角跟蹤誤差來修正波束指向,并更新此信號處理周期對應的初始波束指向以及SDMLF/SDMALF算法中的目標跟蹤向量[13]。

另一方面,如圖3所示的角跟蹤系統,其主體部分為角跟蹤環路,捷聯解耦模塊部分只按照解耦周期完成對當前波束指向的修正,文中所提SDMLF及SDMALF算法可提高此修正值的精度,其中的環路濾波器帶寬不會影響角跟蹤系統中的其他環路。

3　計算機仿真

為驗證本文所提SDMLF及SDMALF算法的有效性,計算機仿真了將靜止目標置于雷達導引頭法線方向,且彈體在3個姿態角方向上均存在擾動的4種場景:

(1) 場景1為角速度測量值準確的情形,即由角速度傳感器得到準確的彈體擾動角速度;

(2) 場景2為角速度測量值存在噪聲的情形,即角速度傳感器得到的含有測量噪聲的彈體擾動角速度;

(3) 場景3為角速度傳感器存在零漂的情形,即由于角速度傳感器由于較長時間工作,得到的擾動角速度值由于溫度變化等原因,產生了零漂,影響了角速度測量值的準確性;

(4) 場景4為彈體擾動加劇，此場景仿真了在彈體飛行過程中,由于空氣阻力擾動等原因,使得彈體擾動的情況加劇,角速度傳感器得到的測量值逐步發散的場景。

為了更加充分地比較本文算法的改進效果,在場景1與場景2中,均分別比較了彈體擾動角速度較小與較大的兩種情況。

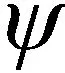
場景1～場景3中彈體的小彈體角速度為

(21)

場景1和場景2中彈體的大彈體角速度為

(22)

場景4中的彈體角速度為

(23)

場景2中分大信噪比(signal-to-noise ratio, SNR)與小SNR兩種情況。大SNR情況下,角速度值中測量噪聲標準差為1°/s;小SNR情況下,角速度值中測量噪聲標準差為4°/s,噪聲均服從正態分布,故場景2中共有4種情況。場景3中,角速度傳感器的零漂為0.2°/s。

3.1　場景1角速度測量值準確

角速度值準確的場景中,將未使用SDM與3種SDM得到的波束指向進行情況對比。本文提出的兩種解耦算法的效果都較為明顯,在表 1中給出了所有場景下,3種解耦算法所得到的解耦后的指向誤差的均方根誤差(root mean square error, RMSE)。

為更簡潔地表現解耦算法所得的性能,考慮到受擾動波束指向的變化曲線基本一致,后續場景中不再將其加入。

(1) 小角速度

圖4為角速度值準確且較小的場景下,幾種解耦方法與波束指向不解耦時的對比曲線。

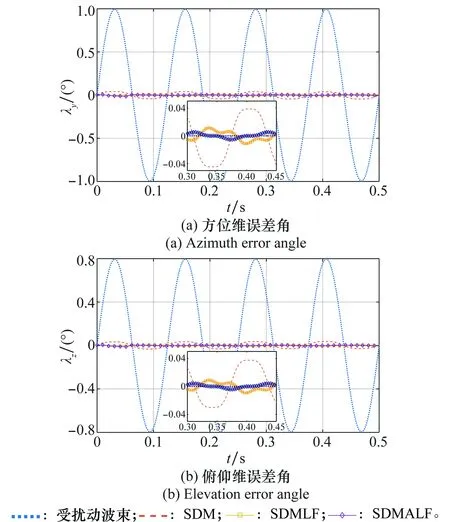
圖4　角速度值準確的小角速度場景

(2) 大角速度

圖5為角速度值準確且較大的場景下,幾種解耦方法與波束指向不解耦時的對比曲線。

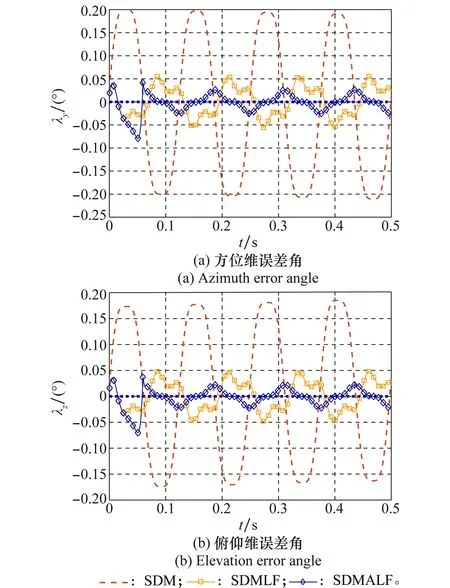
圖5　角速度值準確的大角速度場景

3.2　場景2角速度測量值存在噪聲

在不同大小的角速度測量噪聲,不同姿態轉動角速度的仿真場景中,相比于角速度測量值準確的場景,SDM的解耦性能變差,SDMLF與SDMALF算法的解耦精度均高于SDM算法,其中SDMALF算法仍然表現最好。

(1) 小角速度,大信噪比

圖6為角速度測量值較小且信噪比較大的場景下,幾種解耦方法與波束指向不解耦時的對比曲線。

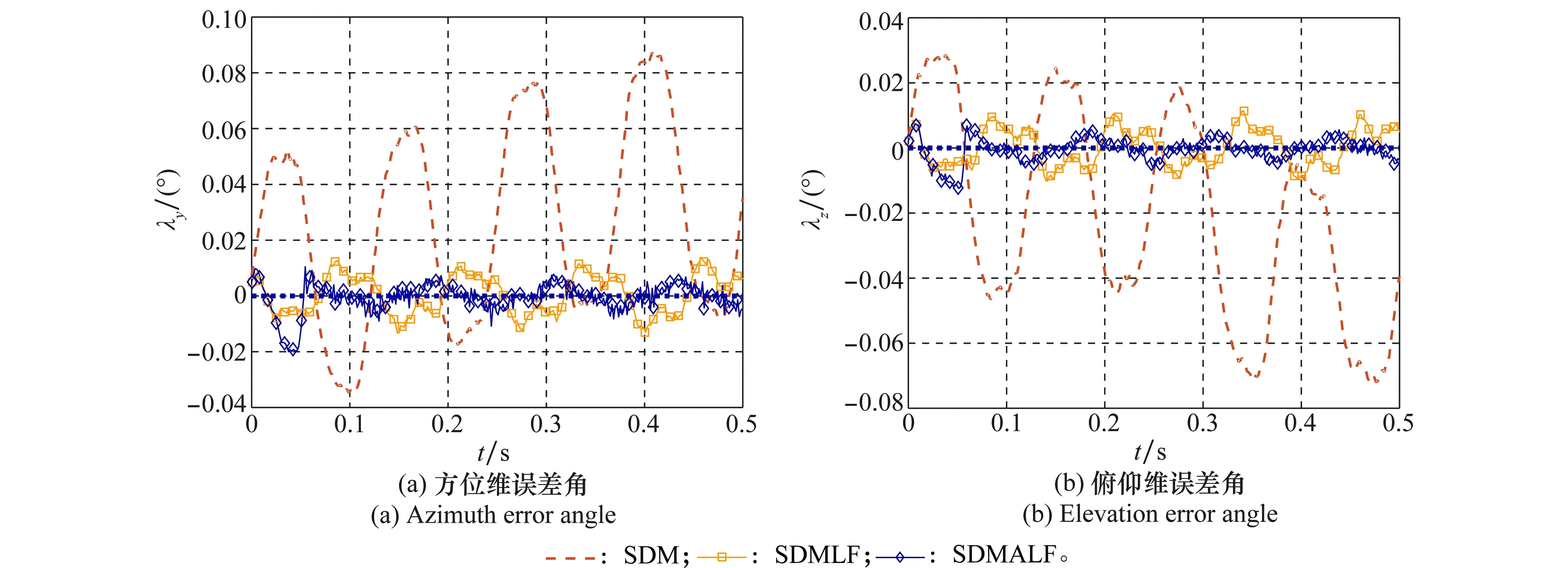
圖6　大信噪比的小角速度場景

(2) 小角速度,小信噪比

圖7為角速度測量值較小且信噪比較小的場景下,幾種解耦方法與波束指向不解耦時的對比曲線。

圖7　小信噪比的小角速度場景

(3) 大角速度,大信噪比

圖8為角速度測量值較大且信噪比較大的場景下,幾種解耦方法與波束指向不解耦時的對比曲線。

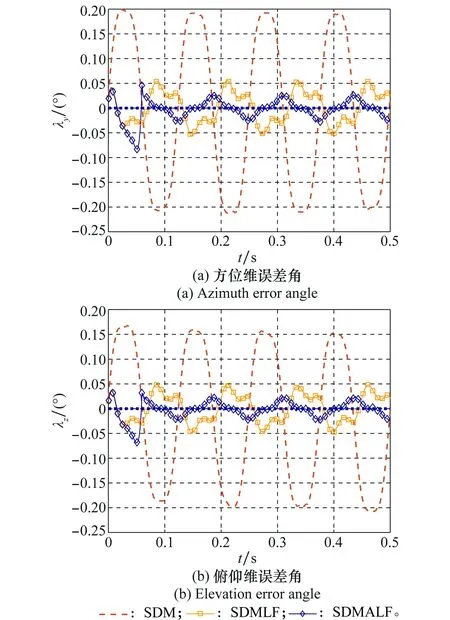
圖8　大信噪比的大角速度場景

(4) 大角速度,小信噪比

圖9為角速度測量值較大且信噪比較小的場景下,幾種解耦方法與波束指向不解耦時的對比曲線。

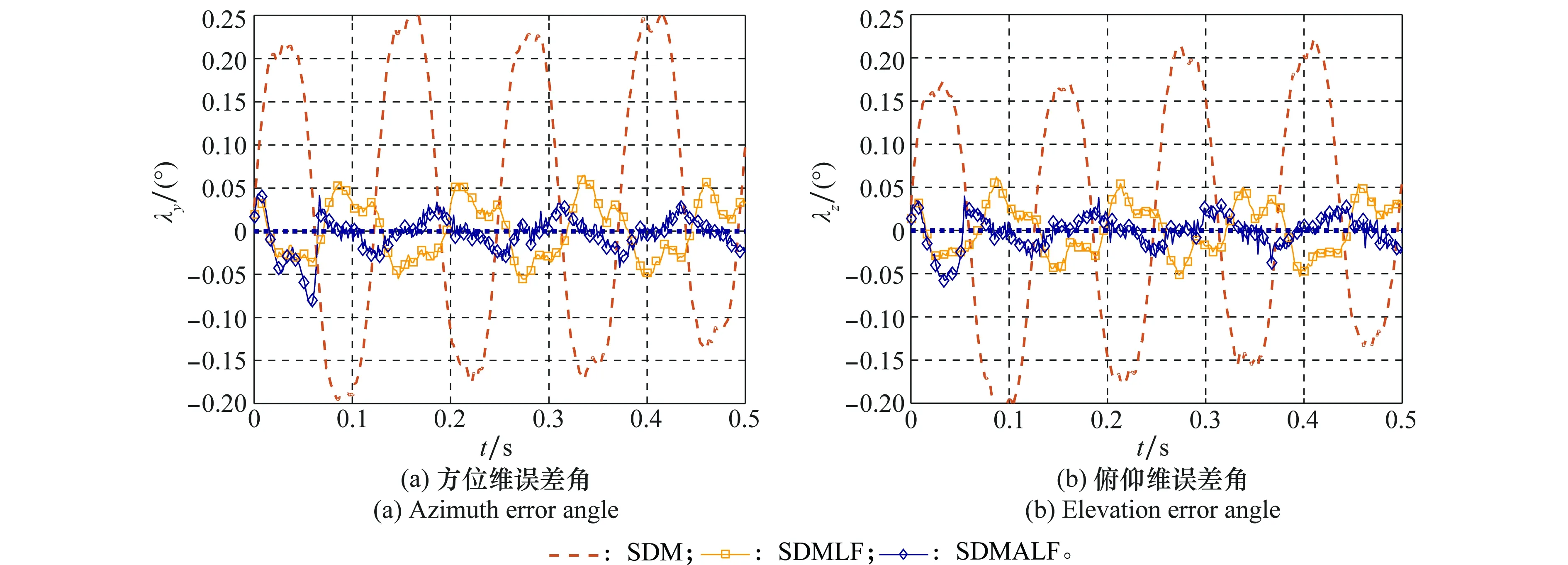
圖9　小信噪比的大角速度場景

3.3　場景3角速度傳感器存在零漂

圖10為角速度傳感器存在零漂時,幾種解耦方法的性能對比。采用SDM算法解耦后,實時計算得到的彈體姿態發生明顯偏差,但SDMLF與SDMALF算法仍然能夠保證穩定的解耦性能。

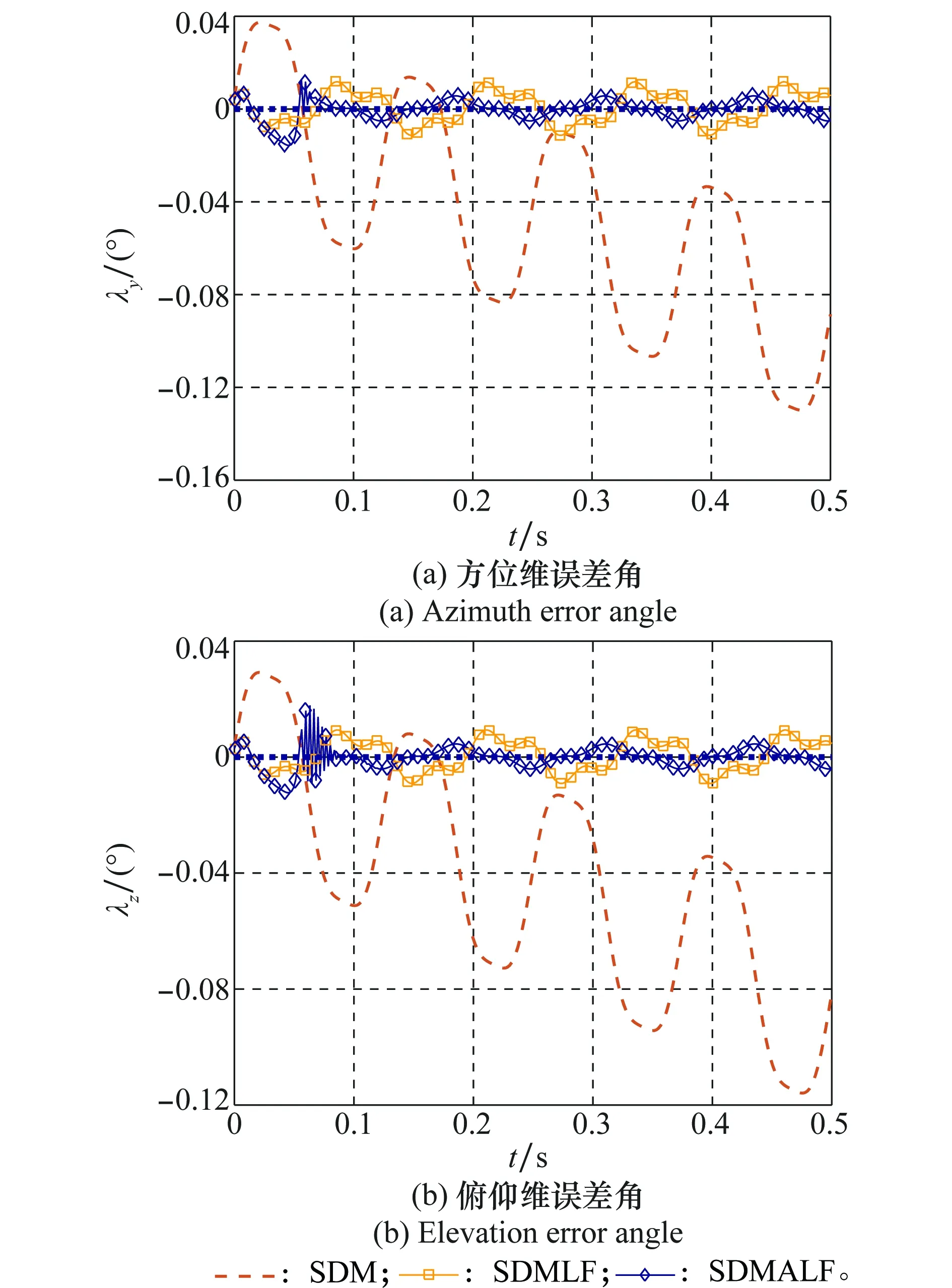
圖10　角速度傳感器存在零漂場景

3.4　場景4彈體擾動加劇

圖11為彈體擾動加劇時,幾種解耦方法的性能對比。可以看出,SDM算法已經失效,SDMLF算法得到的解耦指向開始出現明顯的發散現象,但是SDMALF算法仍能穩定解耦。

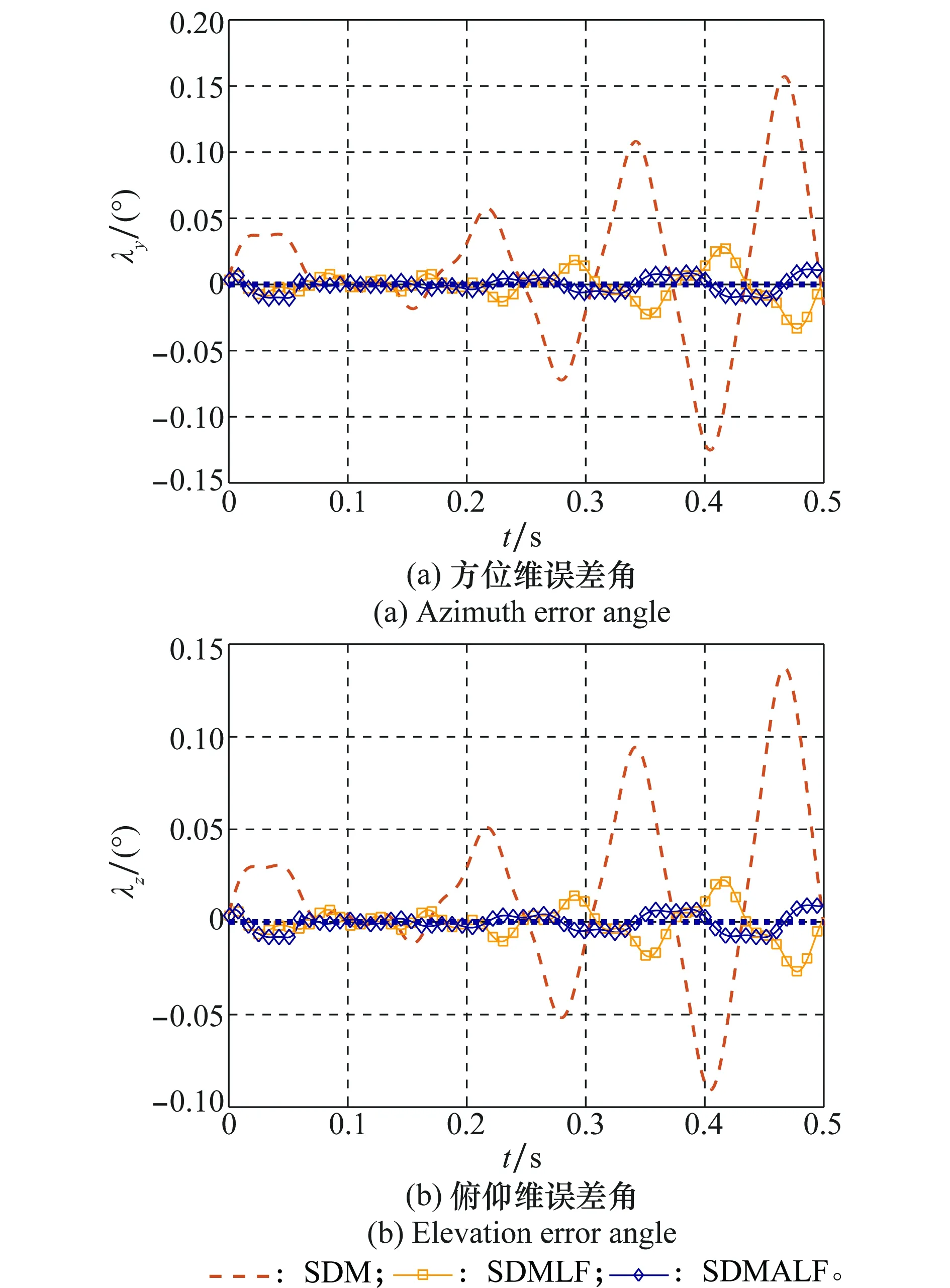
圖11　彈體擾動加劇場景

表1為3種SDM的RMSE對比,分析比較可知,在不存在測量噪聲的場景1,場景3,場景4中,SDMALF方法所得波束指向的RMSE為SDM方法的11.1%左右,為SDMLF方法的58.5%左右。因此,在不存在噪聲時,SDMALF方法對SDM方法的改進效果明顯,可以將解耦精度提高約一個數量級。

表1　3種SDM的RMSE對比

在場景2的小角速度大測量噪聲的情形下,SDMALF對SDM的解耦精度改進最差,約為SDM方法RMSE的16.8%,同時約為SDMLF方法RMSE的84.5%,在此種場景下,SDMALF方法的效果與SDMLF幾乎一致。在場景2的其他3種情形中,SDMALF方法的解耦性能提升較為統一,所得波束指向的RMSE為SDM方法的12.0%左右,為SDMLF方法的58.9%左右.

從以上4種典型的導引頭捷聯解耦場景中可以看出,改進得到的SDMALF算法可以更好地完成對相控陣導引頭的捷聯解耦任務。

4　半實物仿真系統實測結果

為了更好地驗證本文所提出SDMLF與SDMALF算法的正確,利用現有的半實物仿真系統[21]進行了實際測試。實測所采用的半實物仿真系統如圖12所示。

圖12　半實物仿真系統

在半實物平臺上做了3組實驗,依次為:

(1) 場景1:角速度測量值準確;

(2) 場景2:角速度測量值含噪;

(3) 場景3:角速度測量值存在零漂。

其中,模擬信號源中模擬生成的平臺擾動頻率為fM=8.009 Hz,目標在彈體坐標系oxyz中的俯仰角為0.5°,方位角為0.5°,測量噪聲的標準差為2°/s,角速度的零漂為0.1°/s,彈體3個軸向的角速度分別為

(24)

4.1　場景1 角速度測量值準確

圖13中給出了角速度測量值準確場景下,3種算法解耦性能的對比曲線。

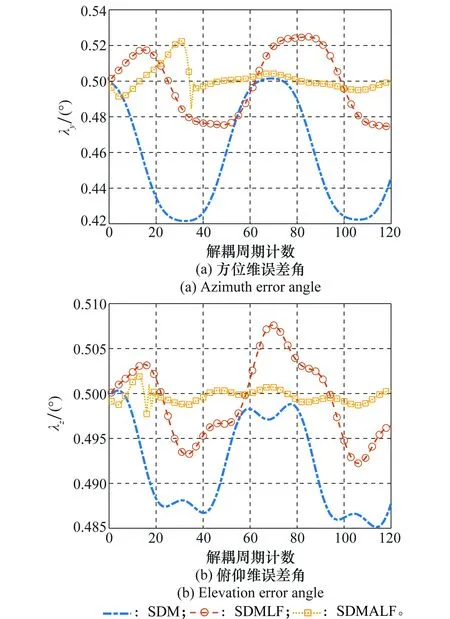
圖13　角速度值準確場景

4.2　場景2 角速度測量值含噪

圖14中給出了角速度測量值含噪場景下,3種算法解耦性能的對比曲線。

4.3　場景3角速度測量值存在零漂

圖15中給出了角速度測量值存在零漂場景下,3種算法解耦性能的對比曲線。

從這3種半實物仿真結果看來,本文所提算法的解耦性能與計算機仿真一致,且SDMALF算法的解耦性能明顯優于SDM算法,進一步驗證了本文算法的正確性及有效性。

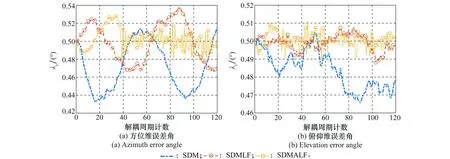
圖14　角速度值含噪場景

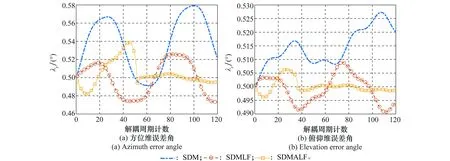
圖15　角速度存在零漂場景

具體的RMSE對比如表 2所示。在半實物仿真系統中,由于實際硬件芯片及系統的原因,得到的RMSE性能不如計算機仿真的結果好,但是本文所提算法性能的提高也較為明顯。在沒有測量噪聲的場景1中,SDMALF算法的RMSE為SDM方法的18.3%左右,為SDMLF方法的26.7%左右。在場景2中,SDMALF算法的RMSE為SDM方法的40.3%左右,為SDMLF方法的48.5%左右。在存在零漂的場景3中,SDMALF算法的RMSE為SDM方法的41.1%左右,為SDMLF方法的59.3%左右。

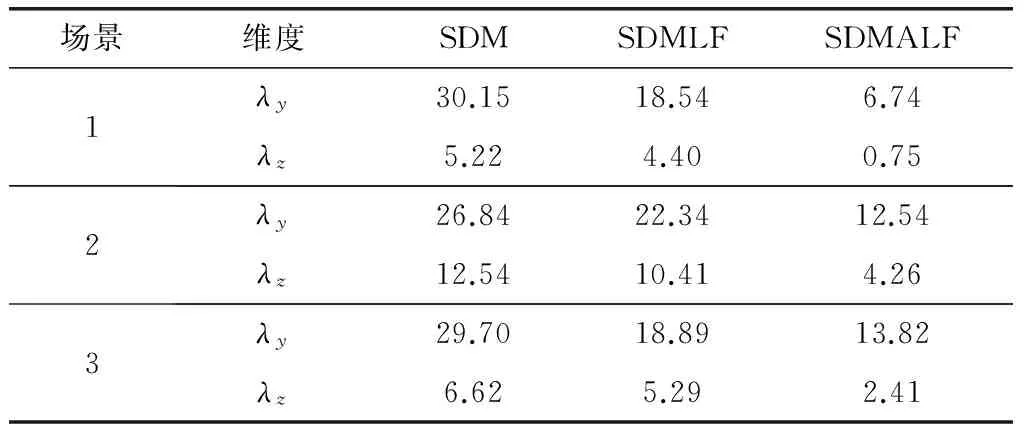
表2　半實物平臺3種方法RMSE對比

在3個場景中,隨著解耦周期的進行,SDMALF得到了穩定的等效環路噪聲帶寬,其解耦后得到的指向都極為接近初始波束指向。

5　結束語

本文設計了兩種相控陣導引頭SDM,有效實現了對被擾動波束指向的閉環控制。通過計算機仿真與半實物平臺的實際測試,驗證了本文設計的基于環路濾波的SDM準確有效,且易于工程實現。提出的SDMALF方法相比于主流SDM,可以自適應地調整等效環路噪聲帶寬,在各種典型彈體擾動場景下的解耦性能更優。

相控陣導引頭系統穩定跟蹤目標的能力與彈體視線角速度信號的輸出品質密不可分。文中所提方法對整個視線角速度提取回路的影響有待后續進一步研究。

參考文獻：

[1] DU X, XIA Q L. The research of guidance performance of the phased array seeker with platform for air-to-air missile[J].Optik-International Journal for Light and Electron Optics,2016,127(22):10322-10334.

[2] BAI R,XIA Q L,DU X.The study of guidance performance of a phased array seeker with platform[J].Optik-International Journal for Light and Electron Optics,2016,132.

[3] 樊會濤, 閆俊. 相控陣制導技術發展現狀及展望[J]. 航空學報, 2015, 36(9):2807-2814.

FAN H T, YAN J. Development and outlook of active electronically scanned array guidance technology[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2807-2814.

[4] 樊會濤,楊軍,朱學平.相控陣雷達導引頭波束穩定技術研究[J]. 航空學報,2013, 34(2):387-392.

FAN H T, YANG J, ZHU X P. Research on beam stabilization technology of phased array radar seeker[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2):387-392.

[5] 李秋生.相控陣雷達導引頭捷聯去耦技術研究[J].制導與引信,2005,26(2):19-22.

LI Q S. Strapdown decoupling technique research on phased array radar seeker[J]. Guidance & Fuze, 2005, 26(2):19-22.

[6] 葉昌. 彈載相控陣導引頭捷聯去耦技術研究[D]. 哈爾濱:哈爾濱工程大學, 2013.

YE C. Strapdown decoupling on phased array seeker of missile[D]. Harbin: Harbin Engineering University, 2013.

[7] 楊建鋒. 相控陣雷達導引頭捷聯解耦技術研究[J]. 制導與引信, 2015, 36(3):1-6.

YANG J F. Development and outlook of active electronically scanned array guidance technology[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 1-6.

[8] 朱振虹, 夏群利, 蔡春濤,等. 相控陣導引頭去耦及視線角速率提取算法研究[J]. 戰術導彈技術, 2013,34(5):70-75.

ZHU Z H, XIA Q L, CAI C T, et al. Research on phased array seeker decoupling and line-of-sight rate extraction algorithm[J]. Tactical Missile Technology, 2013,34(5):70-75.

[9] 王琪,付書堂.捷聯導引頭去耦算法研究[J].航空兵器,2012,48(6):7-9.

WANG Q, FU S T. Decoupling algorithm on strapdown seeker[J]. Aero Weaponry, 2012,48(6):7-9.

[10] 曲圣杰, 陶利, 鄭陶冶. 相控陣導引頭捷聯去耦方法及性能分析[J]. 雷達科學與技術, 2015,22(3):254-258.

QU S J, TAO L, ZHENG T Y. Strapdown decoupling method and performance analysis of phased array radar seeker[J]. Radar Science and Technology, 2015,22(3):254-258.

[11] 孫婷婷, 儲海榮, 賈宏光,等. 捷聯式光學導引頭視線角速率解耦與估計[J]. 紅外與激光工程, 2014, 43(5):1587-1593.

SUN T T, CHU H R, JIA H G, et al. Line-of-sight angular rate decoupling and estimation of strapdown optical seeker[J]. Infrared and Laser Engineering, 2014, 43(5):1587-1593.

[12] DU X, XIA Q. Research on strap down seeker guidance information for rolling interceptor[J].Optik-International Journal for Light and Electron Optics,2016,129:183-199.

[13] 李陽, 肖增利, 孫芃,等. 相控陣雷達捷聯波束穩定方法[J]. 航空學報, 2014, 35(2):497-505.

LI Y, XIAO Z L, SUN P, et al. Strapdown beam stabilization method for phased array radar[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2):497-505.

[14] 魯天宇,尹健,夏群利,等.基于波束角誤差補償的相控陣導引頭解耦算法[J].系統工程與電子技術,2015,37(9):2123-2128.

LU T Y, YIN J, XIA Q L, et al. A kind of decoupling algorithm of phased array seeker based on beam angle error compensation[J].Systems Engineering and Electronics,2015,37(9):2123-2128.

[15] 周瑞青,呂善偉,劉新華.彈載捷聯式天線平臺兩種穩定實現方法的比較[J].系統工程與電子技術,2005,27(8):1397-1400.

ZHOU R Q, Lü S W, LIU X H. Comparison of two stabilization methods for airborne strapdown antenna platform[J]. Systems Engineering and Electronics, 2005, 27(8):1397-1400.

[16] WEN Q Q, LU T Y, XIA Q L, et al. Beam-pointing error compensation method of phased array radar seeker with phantom-bit technology[J]. Chinese Journal of Aeronautics, 2017, 30(3):1217-1230.

[17] GUO T, XIA Q, QI Z. Study on strapdown decoupling technology for rolling missile using RF interferometer seeker[C]∥Proc.of the 3rd IEEE International Symposium on Systems and Control in Aeronautics and Astronautics, 2010: 823-828.

[18] 周瑞青,呂善偉,劉新華.捷聯式天線平臺的角跟蹤系統設計[J].系統工程與電子技術,2003,25(10):1200-1202.

ZHOU R Q, Lü S W, LIU X H. Design of an angle tracking system with strapdown antenna platform[J]. Systems Engineering and Electronics, 2003, 25(10):1200-1202.

[19] 趙妍. 捷聯導引頭解耦系統的研制[D]. 哈爾濱:哈爾濱工程大學, 2007.

ZHAO Y. Development of decoupling system of strapdown seeker[D].Harbin:Harbin Engineering University,2007.

[20] CHUNG B Y, CHIEN C, SAMUELI H, et al. Performance ana-lysis of an all-digital BPSK direct-sequence spread-spectrum IF receiver architecture[J]. IEEE Journal on Selected Areas in Communications, 1993,11(7):1096-1107.

[21] 周春浩.子陣級數字陣列雷達中頻半實物仿真系統設計與實現[D].南京: 南京理工大學, 2015.

ZHOU C H. Design and realization of subarray digital radar IF semi-physical simulation system[D]. Nanjing: Nanjing University of Science and Technology, 2015.