區間變時滯不確定系統魯棒穩定性分析
吳玉彬, 張合新, 惠俊軍, 李國梁, 周 鑫, 孫大為
(1. 火箭軍工程大學控制工程系, 陜西 西安710025; 2.中國人民解放軍96037部隊, 陜西 寶雞 721013; 3. 火箭軍士官學校基礎系, 山東 青州 262500)
0 引 言
現實世界的許多動力學模型系統,例如網絡控制系統、過程控制系統以及核反應堆控制系統等,在數據和物質的傳輸過程中,都包含非常明顯的時滯。在眾多的時滯類型中,區間變時滯更具代表性,它的時滯下界不一定為零,且時滯處于一個變化的區間內,常見于化學反應器、內燃機和網絡控制等工程實際應用中。因而近年來,區間變時滯系統的穩定性分析[1-30]成為熱門的研究領域。
對于區間時滯系統的穩定性分析,最常見的方法是采用基于時域內直接構造Lyapunov-Krasovskii泛函(Lyapunov-Krasovskii function, LKF)并結合線性矩陣不等式(linear matrix inequality, LMI)對其穩定性進行分析。在此框架下,如何降低所得結論的保守性便成為普遍關注的熱點問題。就分析方法而言,有增廣泛函法、自由權矩陣方法和時滯分割方法等。這些方法的共同點在于能充分利用系統的時滯信息,有效降低結論的保守性。但是隨著矩陣變量的過多引入及分割數目的不斷增加勢必給理論分析和工程計算帶來負擔;于是,具有形式簡單、含矩陣變量少的積分不等式界定技術作為新穎的分析方法逐漸給時滯系統的穩定性分析帶來了推動作用。例如,文獻[2]最早把Jensen’s不等式引入到時滯系統的穩定性分析中,隨后文獻[9-11]對Jensen’s不等式做了進一步推廣,從而得到結論保守性更低的相關結論。
文獻[13-14]通過凸組合技術,獲得時滯系統穩定性分析的新穎方法。文獻[13]采用交互式凸組合技術,給出LMI形式保守性更低的穩定性新判據。同樣,文獻[14]借助于Jensen’s不等式和交互式凸組合技術,推導出非線性時變時滯系統的穩定性判據。文獻[21]采用凸組合技術估計附加時變項,獲得嚴格約束的非線性時變系數,所得結論在穩定性方面更具優越性。
文獻[22]新構造的LKF包含三重積分泛函項,優化了時滯系統的穩定性條件。文獻[23-24]針對時變時滯的線性系統,通過構造包含三重積分泛函項的LKF,得到了保守性更低的穩定性判據。文獻[25]構造了包含時變時滯信息的新LKF,基于新的積分不等式界定技術得到了區間時變時滯系統的時滯相關魯棒穩定性判據。文獻[29]通過構造時滯分割LKF,避開凸組合技術和自由權矩陣方法,僅僅采取更嚴格的界定不等式條件,給出了區間時變時滯離散系統的穩定性判據。文獻[30]研究了一類不確定T-S模糊區間時變時滯系統的魯棒穩定性,通過構造包含時滯分割特性的適當LKF,借助于更緊密界定技術的積分不等式處理交叉項,最后用數例證明了給出的穩定性條件在計算效率上具有更小的保守性。
本文針對一類區間變時滯不確定系統,提出形式簡單、保守性更低的魯棒穩定判據。該判據采用新型的時滯分割法,把時滯區間分成不均勻的兩個分割區間,針對每一分割區間構造新的LKF,并采用積分不等式和交互式凸組合技術給出不包含任何多余參量的LMI形式結論。不同于以往方法,①在構造LKF時加入包含更多時滯信息的四重積分項和增廣泛函項;②在處理泛函導數的交叉項時,在未忽略有用項的前提下,利用縮放程度更小的積分不等式進行界定,有利于降低結論的保守性;③采用交互式凸組合技術推導出保守性更低的穩定性判據。最后的數值仿真對比驗證了本文所提判據的有效性與優越性。
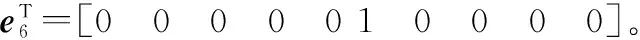
1 問題描述
考慮線性區間變時滯不確定系統
(1)
式中,x(t)∈Rn為系統的狀態向量;A和B為適當維數的系統矩陣;h(t)為系統狀態時變時滯且滿足:0≤hm≤h(t)≤hM,ΔA(t)和ΔB(t)為具有范數有界不確定性的時變結構未知矩陣且滿足
(2)
式中,D、Ea和Eb為適當維數的已知矩陣;F(t)是具有可測元的不確定矩陣,且滿足
F(t)TF(t)≤I,?t.
(3)
當F(t)=0時,系統(1)變為標稱系統(4)。
為證明方便,現將需用到的引理歸納如下。
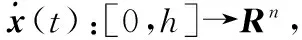
引理2[22]假定任意的矩陣M=MT>0,標量和向量函數x(t):[0,h]→Rn,則有不等式成立,即
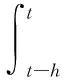
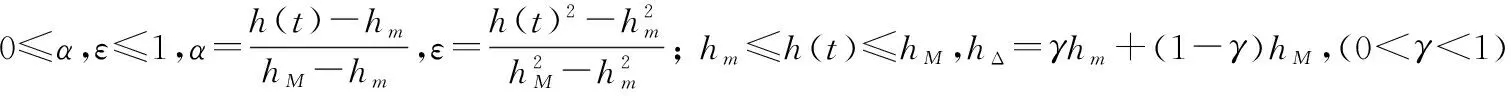
其中
2 主要結論
本小節分兩步討論系統的穩定性,首先給出標稱系統的穩定性判據,其次分析區間變時滯不確定系統的穩定性問題。
系統(1)的標稱系統為
(4)
針對系統(4),通過構造包含時滯信息增廣項和四重積分項的L-K新泛函,結合引理1~引理3有如下結論。
定理1對于給定標量hm、hM和λ1、λ2(λ1>λ2),且若存在正定對稱矩陣Pi(i=1,2,3,4,5)、Q1、Q2、U1、U2、Xj、Rj(j=1,2,3,4),使得式(5)成立,則標稱系統(4)漸近穩定。
Φ=(Φi,j)10×10<0
(5)
其中
Φ13=X2,Φ14=0,Φ15=2P2+hmR2
Φ16=(2-ε)(hM-hm)R4
Φ17=(1+ε)(hM-hm)R4
Φ23=-(α-2)X4,Φ24=(1+α)X4
Φ25=Φ26=Φ27=Φ28=Φ29=Φ210=0
Φ33=Q2-Q1-X2+(α-2)X4
Φ35=-2P2,Φ36=Φ37=2P3
Φ34=Φ38=Φ39=Φ310=0
Φ44=-Q2-(1+α)X4,Φ46=Φ47=-2P3
Φ45=Φ48=Φ49=Φ410=0,Φ55=-X1-R2
Φ56=Φ57=Φ59=Φ510=0,Φ58=-2P4
Φ66=(α-2)X3-(2-ε)R4,Φ67=Φ68=0
Φ69=Φ610=-2P5,Φ77=-(α+1)X3-(1+ε)R4
Φ78=0,Φ79=Φ710=-2P5,Φ88=-R1-U1
Φ89=Φ810=0,Φ99=-(2-ε)R3-U2
Φ910=-U2,Φ1010=(1+ε)R3-U2
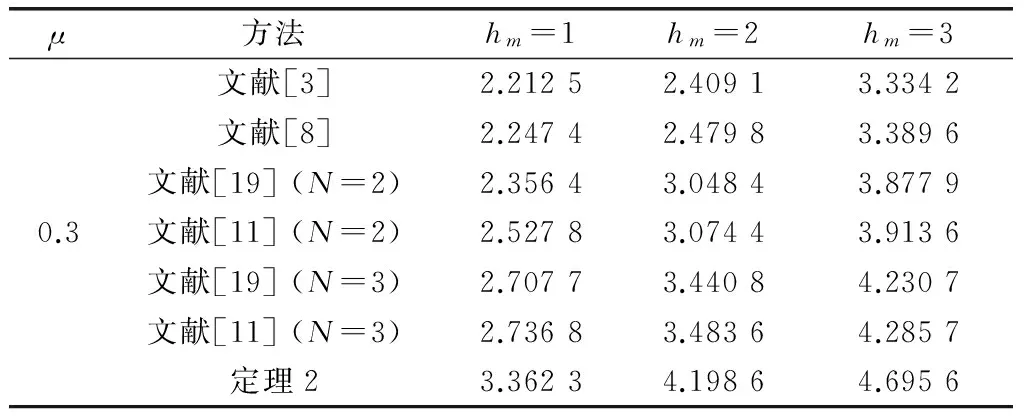
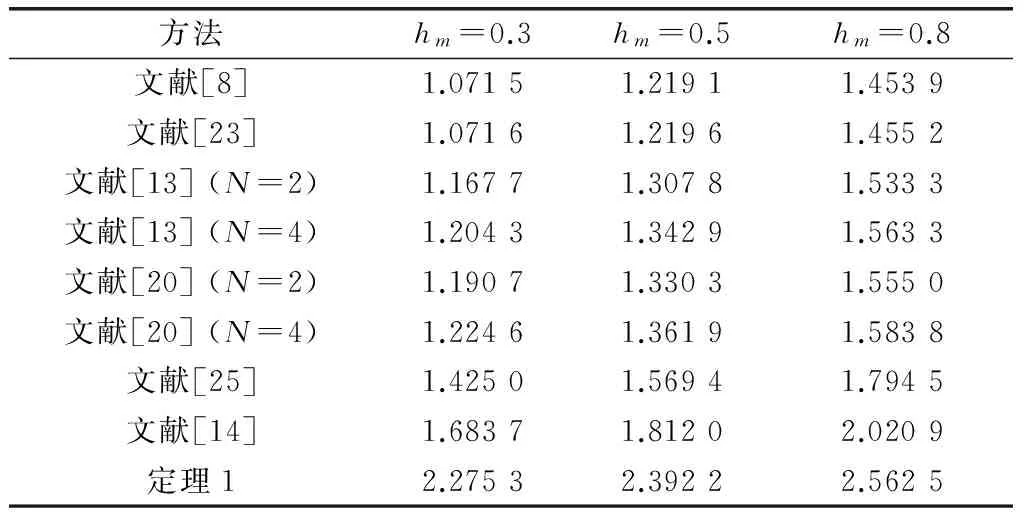
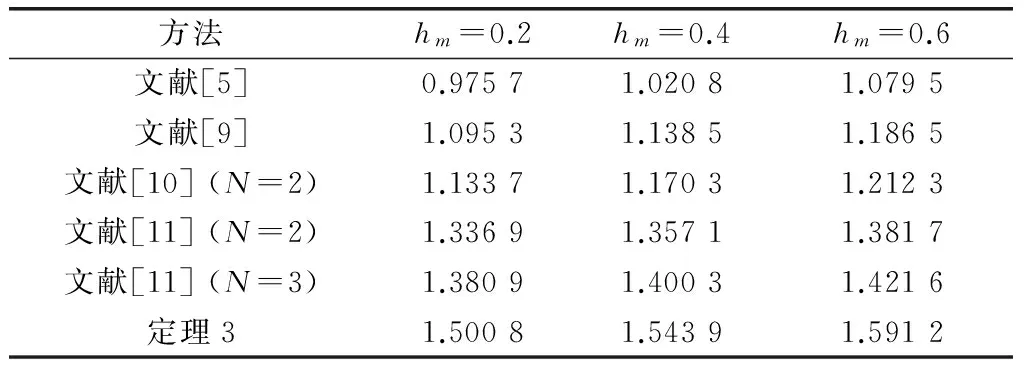
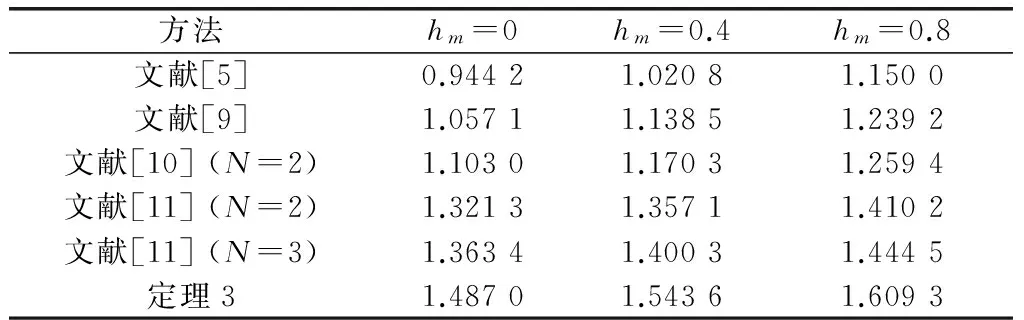
證明令hΔ=γhm+(1-γ)hM, 0<γ<1,則有hm 情形1當hΔ≤h(t)≤hM時,設計LKF為 V(x(t))=V1(x(t))+V2(x(t))+ V3(x(t))+V4(x(t))+V5(x(t)) (6) 其中 計算LKFV(x(t))沿系統(4)的導數,即 (7) 其中 xT(t-hΔ)Q2x(t-hΔ)-xT(t-hM)Q2x(t-hM) 由引理1與引理2可得 (8) (9) 其中,ζ(t)同引理3中hm=hΔ時定義一致。 由引理3可得 (10) 同樣可以得到 (11) (12) (13) (14) (15) (16) (17) ζT(t)[αΓ1+(1-α)Γ2+εΓ3+(1-ε)Γ4]ζ(t) (18) 其中 因為0≤α,ε≤1,根據凸組合技術,不等式(19)、不等式成立,即 α(Γ1+λ1I)+(1-α)(Γ2+λ1I)<0 (19) ε(Γ3-λ2I)+(1-ε)(Γ4-λ2I)<0 (20) 即 αΓ1+(1-α)Γ2<-λ1I (21) εΓ3+(1-ε)Γ4<λ2I (22) 由于λ1>λ2,合并式(21)、式(22),可得 αΓ1+(1-α)Γ2+εΓ3+(1-ε)Γ4<(λ2-λ1)I<0 (23) 情形2當hm≤h(t)≤hΔ時,設計LKF為 V0(x(t))=V01(x(t))+V02(x(t))+ V03(x(t))+V04(x(t))+V05(x(t)) (24) 其中 其中 Pi(i=1,2,3,4,5)、Q1、Q2、U1、U2、Xj、Rj(j=1,2,3,4) 同式(8)中所定義的矩陣。利用同樣的方法,可得 εΓ03+(1-ε)Γ04]ζ0(t) (25) 其中 對式(18)或式(25)應用引理3,則其等價于式(5)。 證畢 注2在式(5)中,新的穩定性判據沒有涉及冗余的自由權矩陣,只是巧妙地采用新穎的積分不等式來界定LKF導數產生的交叉項,并利用極少數自由矩陣表示相關項之間的關系,因此大大減少了理論推導和計算上的復雜性,從而降低了結論的保守性。 注3在式(10)、式(11)和式(14)中,交互式凸組合處理技術[13,27]作為非傳統方法用來更有效地界定LKF導數產生的交叉項,可以得到保守性更低的穩定性結論。 定理2對于給定標量hm、hM和λ1、λ2(λ1>λ2)、μ,且若存在正定對稱矩陣Pi(i=1,2,3,4,5)、Q1、Q2、Q3、U1、U2、Xj、Rj(j=1,2,3,4),使得LMIs成立,即 (26) 下面針對區間變時滯不確定系統(1)的魯棒穩定性問題進行研究。 定理3對于給定標量0 (27) 則不確定系統(1)漸近穩定。其中 證明對于不確系統(1),分別以A+ΔA(t),B+ΔB(t)代替式(4)中的A和B,仿照定理1的證明,可得到系統(1)漸近穩定。 證畢 通過3個具有代表性的數值例子來比較說明本文方法的優越性。利用Matlab的LMI工具箱很容易求得所需要的可行性解。最大允許時延(maximum allowable delay bound, MADB)定義為保證系統穩定的最大允許時滯上界值,是比較時滯系統穩定性結論保守性最普遍的衡量標準。 例1首先考慮區間變時滯閉環控制系統為 針對不同的時滯下界hm,根據式(26)和式(5),分別從時滯變化率μ=0.3和時滯變化率μ取任意值兩個角度,仿真給出相應的MADB值即hM如表1和表2所示。 表1 例1中針對不同的時滯下界,不同方法仿真給出的MADB值 表2 例1中當時滯變化率未知時,不同方法仿真給出的MADB值 由表1和表2可知,本文提出的方法明顯優于已有文獻的結論。 例2考慮區間變時滯不確定系統,即 式中,δ1,δ2,δ3和δ4為未知參數,滿足:|δ1|≤1.6,|δ2|≤0.05,|δ3|≤0.1,|δ4|≤0.3。 針對不同的時滯下界hm,根據式(26),仿真給出相應的MADB值即hM如表3所示。 表3 例2中針對不同的時滯下界,不同方法仿真給出的MADB值 由表3的比較結果可知,對于本例而言,本文方法改善了現有文獻[5,9,16,25]的結論。 例3考慮另一區間變時滯不確定系統,其系統參數為 根據式(27),針對不同的時滯下界hm,當時滯變化率未知時,仿真給出相應的MADB值即hM如表4所示。 表4 例3中針對不同的時滯下界,不同方法仿真給出的MADB值 由表4可知,本文所提出的穩定性判據擴大了保證系統穩定的最大允許時滯上界范圍,具有更低的保守性。 針對一類區間變時滯不確定系統的魯棒穩定性問題進行了分析研究。基于新型的非均勻時滯分割法,通過構造包含四重積分增廣泛函項的新LKF,提出了基于LMI的穩定性新判據。為了提高計算效率并簡化結論,該判據避免使用模型變換與自由權矩陣界定技術,取而代之的是采用具有更緊密界定技術的積分不等式和交互式凸組合技術,從而充分利用了時滯下界信息,獲得了保守性更低的結論。最后,數值仿真證明了所得判據相比較已有文獻中的方法,擴大了系統穩定所允許的最大時滯上界范圍,更具優越性與競爭性。 參考文獻: [1] GAHINET P, NEMIROVSKI A, LAUB A J, et al. LMI control toolbox user’s guide[J].1995. [2] GU K, KHARITONOV V L, CHEN J. Stability of time-delay systems[M]. Boston: Birkh?user, 2003. [3] HE Y, WANG Q G, LIN C, et al. Delay-range-dependent stability for systems with time-varying delay[J].Automatica,2007,43(2): 371-376. [4] HE Y, WANG Q C, XIE L, et al. Further improvement of free weighting matrices technique for systems with time-varying delay[J]. IEEE Trans.on Automatica Control, 2007, 52(2): 293-299. [5] JIANG X F, HAN Q L. New stability criteria for linear systems with interval time varying delay[J]. Automatica, 2008, 44(10): 2680-2685. [6] PENG C, TIAN Y. Delay-dependent robust stability criteria for uncertain systems with interval time-varying delay[J]. Journal of Computational and Applied Mathematics, 2008, 214(2): 480-494. [7] SHAO H. Improved delay-dependent stability criteria for systems with a delay varying in a range[J]. Automatica,2008,44(12): 3215-3218. [8] SHAO H Y. New delay-dependent stability criteria for systems with interval delay[J]. Automatica, 2009, 45(3): 744-749. [9] RAMAKRISHNAN K, RAY G. Delay-dependent robust stability criteria for linear uncertain systems with interval time varying delay[C]∥Proc.of the TENCON 2009-2009 IEEE Region 10 Conference, 2009: 539-543. [10] RAMAKRISHNAN K, RAY G. Robust stability criteria for uncertain linear systems with interval time-varying delay[J]. Journal of Control Theory and Applications, 2011, 9(4): 559-566. [11] 張合新,惠俊軍,周鑫,等.基于時滯分割法的區間變時滯不確定系統魯棒穩定新判據[J].控制與決策,2014,29(5):907-912. ZHANG H X, HUI J J, ZHOU X, et al. New robust stability criteria for uncertain systems with interval time-varying delay based on delay-partitioning approach[J]. Control and Decision, 2014, 29(5): 907-912. [12] YUE D, TIAN E, WANG Z, et al. Stabilization of systems with probabilistic interval input delays and its applications to networked control systems[J]. IEEE Trans.on Systems, Man and Cybernetics, 2009, 39(4): 939-945. [13] ZHU X L, WANG X Y, YANG G H. New stability criteria for continuous-time systems with interval time-varying delay[J]. IET Control Theory Applications, 2010, 4(6): 1101-1107. [14] AN J Y, LI Z Y, WANG X M. A novel approach to delay-fractional dependent stability criterion for linear systems with interval delay[J]. ISA Trans., 2014, 53(2): 210-219. [15] ZHANG W, CAI X S, HAN Z Z. Robust stability criteria for systems with interval time-varying delay and nonlinear perturbations[J]. Journal of Computational and Applied Mathematics, 2010, 234(1): 174-180. [16] PARK P, KO J W, JEONG C. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47(1): 235-238. [17] KWON O M, LEE S M, PARK J H. Linear matrix inequality approach to new delay-dependent stability criteria for uncertain dynamic systems with time-varying delays[J]. Journal of Optimization Theory Applications, 2011, 149(3): 630-646. [18] LI T, SONG A, XUE M, et al. Stability analysis on delayed neural networks based on an improved delay-partitioning approach[J]. Journal of Computational and Applied Mathematics, 2011, 235(9): 3086-3095. [19] WANG C, SHEN Y. Delay partitioning approach to robust stability analysis for uncertain stochastic systems with interval time-varying delay[J]. IET Control Theory and Applications, 2012, 6(7): 875-883. [20] TANG M, WANG Y W, WEN C. Improved delay-range-dependent stability criteria for linear systems with interval time-varying delays[J]. IET Control Theory and Applications, 2012, 6(6): 868-873. [21] PHAT V N, KHONGTHAM Y, RATCHAGIT K. LMI approach to exponential stability of linear systems with interval time-varying delays[J]. Linear Algebra and Its Applications, 2012, 436(1): 243-251. [22] SUN J, LIU G P, CHEN J. Delay-dependent stability and stabilization of neutral time-delay systems[J]. International Journal of Robust Nonlinear Control, 2009, 19(12): 1364-1375. [23] SUN J, LIU G P, CHEN J, et al. Improved stability criteria for linear systems with time-varying delay[J]. IET Control Theory Applications, 2010, 4(4): 683-689. [24] SUN J, LIU G P, CHEN J, et al. Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J]. Automatica, 2010, 46(2): 466-470. [25] LIU P L. Further improvement on delay-range-dependent stability results for linear systems with interval time-varying delays[J]. ISA Transaction, 2013, 52(6): 725-729. [26] LEE W, PARK P. Second-order reciprocally convex approach to stability of systems with interval time-varying delays[J]. Applied Mathematics and Computation, 2014, 229(10): 245-253. [27] FARNAM A, ESFANJANI R M. Improved linear matrix inequality approach to stability analysis of linear systems with interval time-varying delays[J]. Journal of Computational and Applied Mathematics, 2016, 294(C): 49-56. [28] FARNAM A, MAHBOOBI ESFANJANI R. Improved stabilization method for networked control systems with variable transmission delays and packet dropout[J]. ISA Transaction, 2014, 53 (6): 1746-1753. [29] ZHANG J, PENG C, ZHENG M. Improved results for linear discrete-time systems with an interval time-varying input delay[J]. International Journal of Systems Science, 2015, 47(2): 492-499. [30] PENG C, FEI M R. An improved result on the stability of uncertain T-S fuzzy systems with interval time varying delay[J]. Fuzzy Sets and Systems, 2013, 212(1): 97-109.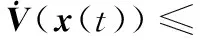
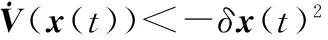
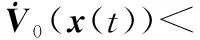
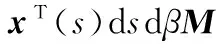
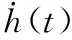
3 數值仿真與比較
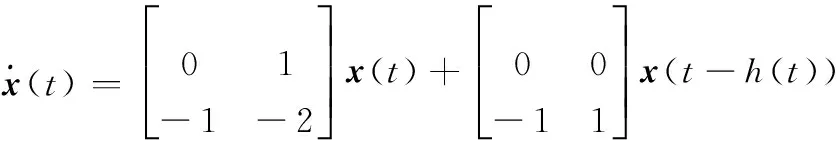
4 結 論

