混沌理論和機器學習算法的運動員成績預測模型

高素霞

摘 要： 為了準確地對運動員成績進行預測，結合運動員成績的具體變化特點，設計了基于混沌理論和機器學習算法的運動員成績預測模型。首先對當前運動員成績建模與預測的研究現狀進行分析，找到當前運動員成績預測模型存在的不足，然后采用混沌理論對運動員成績歷史數據進行處理，發現其中隱藏的規律，最后引入機器學習算法——極限學習機設計運動員成績預測模型。仿真實驗結果表明，與當前運動員成績預測模型相比，所設計模型的運動員成績預測結果更加可靠，而且運動員成績預測精度更高，可以應用于體育科學訓練計劃制定。

關鍵詞： 運動員成績； 機器學習算法； 混沌理論； 原始數據； 成績預測模型； 極限學習機

中圖分類號： TN911.1?34； TP391 文獻標識碼： A 文章編號： 1004?373X（2018）07?0152?04

Athletes performance prediction model based on chaos

theory and machine learning algorithm

GAO Suxia

（Henan Institute of Technology， Xinxiang 450044， China）

Abstract： In order to predict the athletes performance accurately， the specific change characteristics of athletes performance is combined to design the athletes performance prediction model based on chaos theory and machine learning algorithm. The current research status of athletes performance modeling and prediction is analyzed to find the shortcomings of the current athletics performance prediction models. The chaos theory is used to process the athletes′ historical data， and find its hidden rules. The machine learning algorithm （extreme learning machine） is introduced to design the athletes performance prediction model. The simulation and experiment results show that， in comparison with the current athletics performance prediction models， the prediction model has more reliable athletes performance prediction result and higher prediction accuracy， and can be applied to the plan formulation of sports scientific training.

Keywords： athletes performance； machine learning algorithm； chaos theory； initial data； performance prediction model； extreme learning machine

0 引 言

隨著運動競技水平的不斷提高，運動員的成績引起了廣大研究人員的關注，而運動員成績與多種因素如訓練水平、運動員身體素質、運動器材等密切相關[1]。為了保證運動員獲得更理想的成績，需要對運動員成績的變化特點進行準確、全面跟蹤，為此對運動員成績進行建模與預測研究變得越來越重要，成為體育科學研究中的一個重要課題[2]。

研究人員引入了各種各樣的方法對運動員成績展開預測研究[3]，相關研究結果表明，運動員成績之間具有一定的時間相關性，為此有學者采用滑動平均方法建立運動員成績預測模型[4]，其可以對運動員成績的上升趨勢進行描述，但運動員成績并非是一種明顯的上升趨勢，也有下降趨勢、非平穩性，因此，所建立的運動員成績預測模型與實際情況不相符，預測精度較低[5]。隨后，有學者引入非線性理論構建運動員成績預測模型，如各種神經網絡等，該類模型的非線性建模能力相對較優，對運動員成績變化特點可更好的預測，成為當前運動員成績建模與預測的主要工具[6?8]。然而運動員成績是一種混沌數據列，其中隱藏的規律難以顯示出來，為此需要對原始運動員成績進行相空間重構，發現運動員成績的長期變化特點[9?10]。極限學習機是一種近年新興的機器學習算法，比傳統神經網絡的學習速度要快很多倍，而且其預測性能也得到了相應的提高，為運動員成績建模提供了有效的研究工具。

為了準確地對運動員成績進行預測，結合運動員成績的具體變化特點，設計了混沌理論和機器學習算法的運動員成績預測模型。首先采用混沌理論對運動員成績歷史數據進行處理，然后引入極限學習機設計運動員成績預測模型，仿真實驗結果表明，本文模型的運動員成績預測結果更加可靠，而且運動員成績預測精度更高，驗證了本文模型的有效性。

1 混沌理論和極限學習機

1.1 混沌理論

運動員成績與訓練水平、運動員自身素質、運動器材等相關，使得運動員的原始成績具有一定的時間相關性，而且非平穩性，無法直接通過機器學習算法建立運動員預測模型，需要通過混沌理論分析，將原始運動員成績重構成為多維的運動員成績，便于機器學習算法建模。運動員的原始成績為[x（t），][t=1，2，…，n，n]表示運動員成績的點數。采用嵌入維[m]和延遲時間[τ]對[x（t）]進行處理，得到一個多維運動員成績，即有：

根據[F：][Rm→Rm]建立的運動員成績軌跡為：[X（n+mτ）=fx（n），x（n+τ），…，xn+（m-1）τ] （2）

式中[f（ ）]表示運動員成績預測函數。

1.2 極限學習機

設原始運動員成績經過混沌處理后得到的數據為[G={（x1，t1），（x2，t2），…，（xN，tN）}，][xi=[xi1，xi2，…，xin]∈Rn，][ti=[ti1，][ti2，…，tin]∈Rm，][i=1，2，…，N，]那么可以建立如下的極限學習機：

對式（3）進行轉化，建立如下的矩陣形式：

[Hβ=T] （4）

運動員成績具有非線性變化特點時，就要做如下變形，即：

對式（5）進行簡化，加快極限學習機的建模速度，即：

式中[ω=[ω1，ω2，…，ωN]]為拉格朗日乘子。

對式（6）求偏導，得到：

極限學習機的運動員成績預測方程可表示為：

2 混沌理論和機器學習算法的運動員成績模型

基于混沌理論和機器學習算法的運動員成績模型集成了混沌理論挖掘非平穩性變化特點和機器學習算法可以預測非線性變化特點的優點，建立精度高的運動預測模型，工作步驟如下：

1） 對于某一個運動員，對其歷史成績進行收集，并按時間先后排列，構建一維的運動員成績。

2） 為了減少運動員成績波動帶來的干擾，對其進行歸一化操作，使得變化范圍縮小到[0，1]范圍，即：

[x=x-xminxmax-xmin] （9）

式中：[x]表示原始運動員成績；[xmax，][xmin]分別表示運動員成績的最大值和最小值；[x]表示歸一化后的運動員成績。

3） 對歸一化的運動員成績通過混沌理論中的相關算法確定[m]和[τ，]然后通過[m]和[τ]對運動員成績進行重構。

4） 采用極限學習機建立運動員成績預測模型。

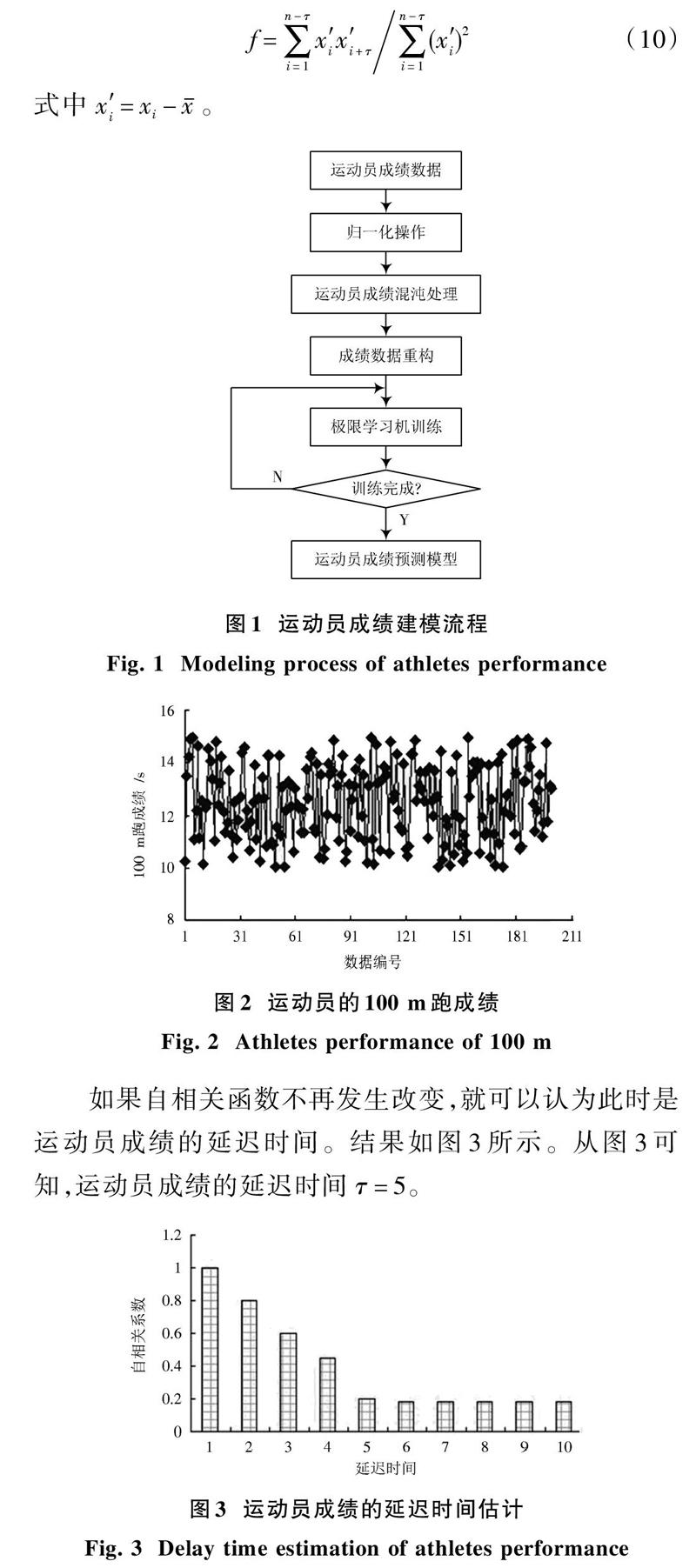
混沌理論和極限學習機的運動員成績建模流程如圖1所示。

3 仿真實驗

3.1 運動員成績

為了分析本文提出的運動員成績預測模型的預測效果，選擇一個運動員100 m跑的成績作為研究對象，收集到200個數據，具體如圖2所示。

3.2 運動員成績的混沌處理

對于運動員的原始成績，需要確定其延遲時間，延遲時間到底多大適合，僅憑經驗無法確定。延遲時間太大，那么運動員成績之間就沒有相關性；延遲時間太小，運動員成績無法完全展開，因此，選擇自相關函數法估計運動員成績的延遲時間。設運動員成績數據為[X=（x1，x2，…，xn），]自相關函數為：

式中[x′i=xi-x]。

如果自相關函數不再發生改變，就可以認為此時是運動員成績的延遲時間。結果如圖3所示。從圖3可知，運動員成績的延遲時間[τ=5。]

采用 G?P算法估計運動員成績的嵌入維數，即有：

1） 從運動員成績中選擇[m]個數據組成序列[vt1i，]采用同樣方式建立另一個序列[vt2i，]不斷重復該過程，建立運動員成績的相空間。

2） 估計運動員成績數據點間的累積分布函數為：

3） 關聯維數[D]和[C（r）]應滿足式（12）：

4） [m=m+1，]重復上述步驟，當[D]變化比較平穩時，可以得到運動員成績的嵌入維數。

運動員成績的嵌入維數?關聯維數變化關系如圖4所示，可以發現，運動員成績的嵌入維數[m=5。]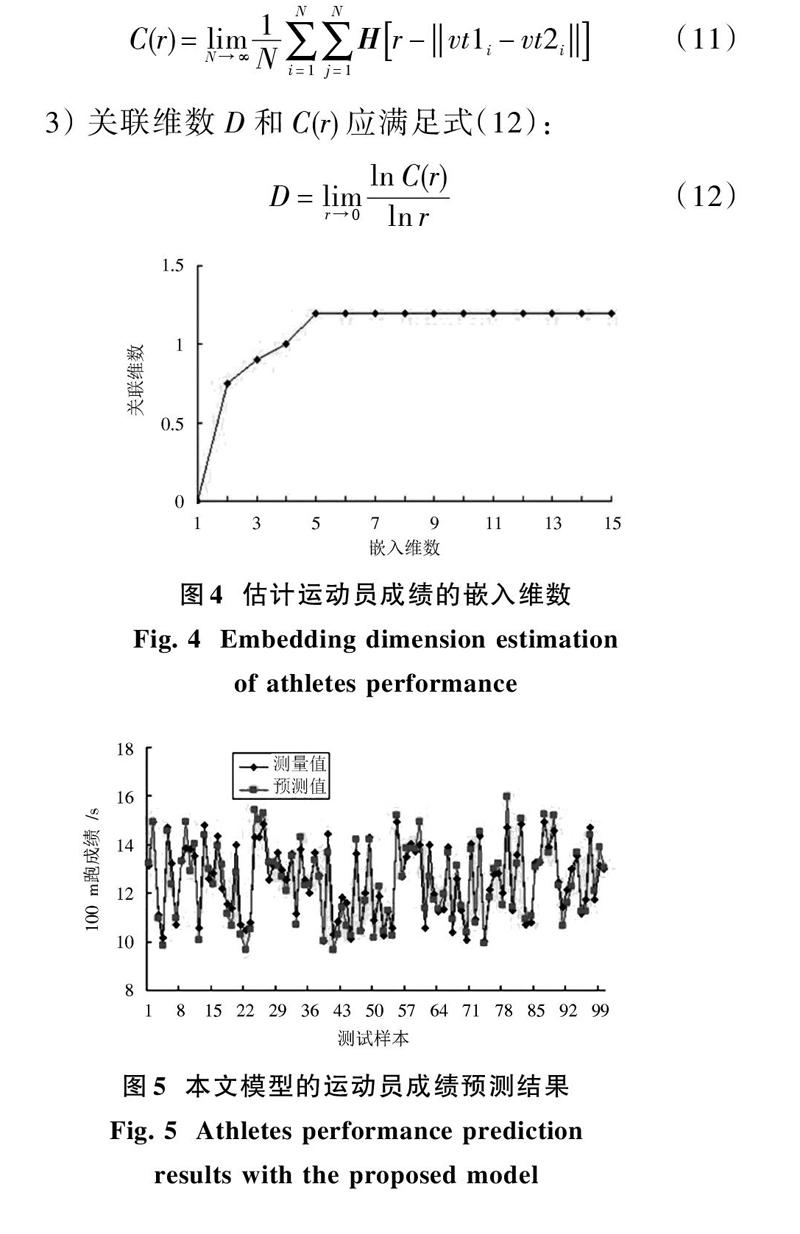

3.3 運動員成績的預測性能分析

對100個運動員的成績測試數據進行建模，成績預測結果如圖5所示。從預測結果可以看出，本文模型可以對運動員成績進行準確預測，獲得較高精度的運動員成績預測結果，是一種有效的運動員成績預測模型。

選擇文獻[9?10]的運動員成績預測模型進行對比實驗，它們的預測精度如表1所示。從表1可知，本文運動員成績預測模型的精度最高，有效降低了運動員成績的預測誤差，預測結果更加可信。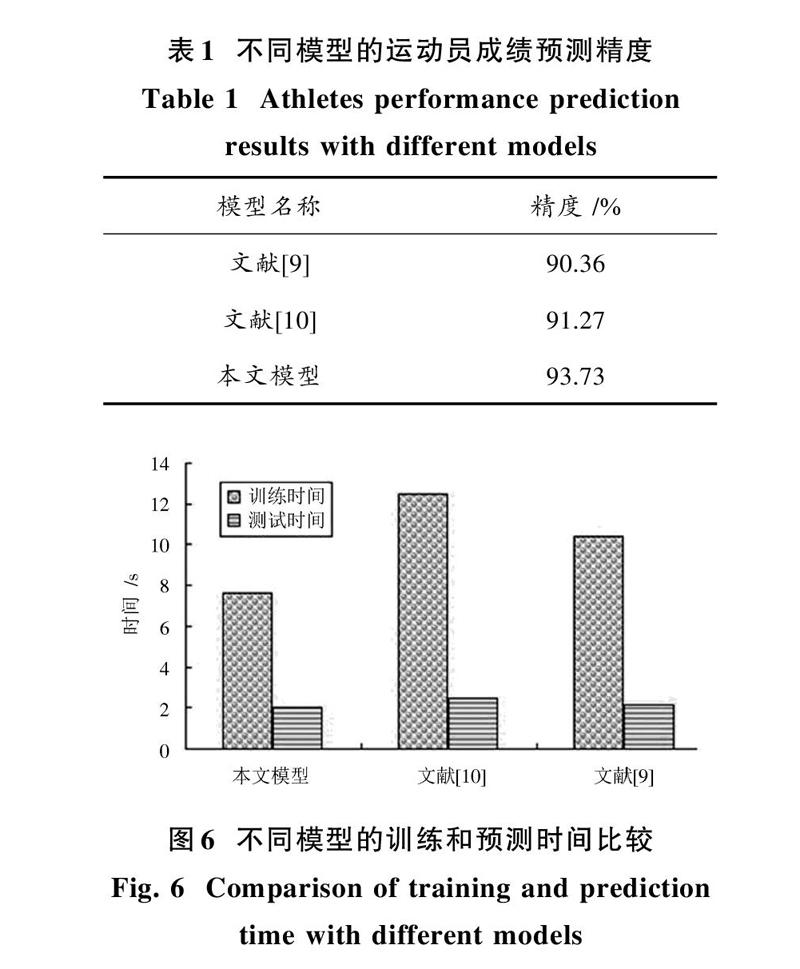

不同模型的運動員成績平均訓練和預測時間如圖6所示。在所有運動員成績預測模型中，本文模型的平均訓練和預測時間最少，大幅度提高了運動員成績建模速度，模型的實際應用范圍得到了擴展。

4 結 語

成績預測問題是當前運動員訓練研究的重點，結合運動員成績變化特點和當前運動員成績建模方法的局限性，提出混沌理論和機器學習算法的運動員成績預測模型，運動員成績具體預測實驗結果表明，該模型克服了其他運動員預測模型的不足，可以對運動員成績變化特點進行高精度的跟蹤，建立了性能優異的運動員成績預測模型，不僅提高了運動員成績的預測精度，而且建模效率高，具有十分廣泛的應用前景。

參考文獻

[1] 許晶.我國頂尖男子十項全能運動員競技特征及實力分析[J].廣州體育學院學報，2008，12（3）：36?64.

XU Jing. Analysis of competitive characteristics and strength of top ten all?around athletes in China [J]. Journal of Guangzhou Sports University， 2008， 12（3）： 36?64.

[2] 趙波.十項全能世界頂尖男子運動員成績分析及預測研究[J].體育文化導刊，2013（3）：76?79.

ZHAO Bo. Performance analysis and prediction of the ten world top men′s decathlon athletes′ [J]. Sports culture， 2013（3）： 76?79.

[3] 趙丙軍.運用多元回歸方法建立我國男子跳遠項目訓練模型的研究[J].西安體育學院學報，2011，18（1）：81?82.

ZHAO Bingjun. Research on the training model of Chinese men′s long jump project by using multiple regression method [J]. Journal of Xian Physical Education University， 2011， 18（1）： 81?82.

[4] 莊沖，王宗平.灰色系統模型與BP神經網絡模型在體育成績預測方面的比較研究[J].南京體育學院學報，2006，20（6）：134?135.

ZHUANG Chong， WANG Zongping. Comparison between grey system model and BP neural network model in sports performance prediction [J]. Journal of Nanjing Sport Institute， 2006， 20（6）： 134?135.

[5] 魏春玲.我國十項全能運動成績的因子分析及灰色系統回歸預測研究[J].體育科學，2004，24（11）：51?53.

WEI Chunling. The factor analysis of the performance of the ten all?around sports in China and the grey system regression prediction study [J]. Sports science， 2004， 24（11）： 51?53.

[6] 鄧美蘭.奧運會男子十項全能前三名成績的灰色預測模型的研究[J].數學的實踐與認識，2009（18）：44?49.

DENG Meilan. The study of the grey prediction model of the men′s ten events in the first three games of the Olympic Games [J]. The practice and understanding of mathematics， 2009（18）： 44?49.

[7] 孫群，劉國璧，程偉，等.基于模糊神經網絡的劉翔110 m欄成績預測[J].重慶科技學院學報（自然科學版），2011，13（2）：135?138.

SUN Qun， LIU Guobi， CHENG Wei， et al. Based on fuzzy neural network， Liu Xiang′s 110 m column performance prediction [J]. Journal of Chongqing University of Science and Technology （natural science edition）， 2011， 13（2）： 135?138.

[8] 李征宇，閆生.神經網絡模型在運動成績預測中的應用[J].哈爾濱體育學院學報，2009，27（2）：110?113.

LI Zhengyu， YAN Sheng. Application of neural network model in the prediction of athletic performance [J]. Journal of Harbin Institute of Physical Education， 2009， 27（2）： 110?113.

[9] 劉昊.非線性篩選因子和加權的體育成績建模與預測[J].計算機應用與軟件，2014，31（11）：105?108.

LIU Hao. Nonlinear screening factor and weighted sports performance modeling and prediction [J]. Computer applications and software， 2014， 31（11）： 105?108.

[10] 成天樂，周勝瑜，李斯，等.基于極限學習機方法的短期負荷預測[J].電力科學與工程，2013，29（4）：24?25.

CHENG Tianle， ZHOU Shengyu， LI Si， et al. Short?term load forecasting method based on extreme learning machine [J]. Electric power science and engineering， 2013， 29（4）： 24?25.