復合MLINEX對稱損失函數下Pareto分布參數的Bayes估計

朱寧，劉慶華，農以寧，蔣東云

（桂林電子科技大學數學與計算科學學院，廣西桂林541004）

0　引言

帕累托（Pareto）分布是收入分配理論中的一種重要的統計分布,最初是由意大利Pareto作為收入分布于1897年提出來的，并指出其是一個具有遞減的失效函數[1]。自從Pareto分布提出以來就被廣泛地運用于金融、保險、災害預測等諸多領域，關于其統計推斷的研究引起了很多學者的關注。近年來，在Bayes思想下Pareto分布參數估計的研究越來越多。韓慧芳等[2]研究了當尺度參數已知時，Pareto分布中形狀參數的估計，一致最小方差無偏估計，并在平方損失和熵損失下討論其可容許等。韋程東等[3]在復合LINEX對稱損失函數下，研究Pareto分布在其尺度參數已知的情況下利用共軛先驗分布求出其形狀參數的E-Bayes估計。井曉培和周菊玲[4]討論了獨立同分布樣本情形廣義Pareto分布參數的經驗Bayes單側檢驗問題，并證明了此經驗Bayes檢驗函數的漸近最優性，獲得了其收斂速度。沈新娣和丁幫俊[5]研究Pareto分布在逐步Ⅱ型區間刪失的情形下參數的估計和性質。韓明[6]研究Pareto分布中形狀參數的估計、一致最小方差無偏估計。并分別在平方損失和熵損失下討論了θ的Bayes估計,研究其容許性。

自從2003年Podder CK[7]提出MLINEX函數以來，越來越多的學者關注MLINEX函數。Podder CK[8]比較Pareto分布參數估計在MLINEX函數和平方損失函數下的不同。任海平[9]分別在加權平方損失函數和MLINEX損失函數下一類分布族參數的Minimax估計。金秀巖[10]在MLINEX損失函數的基礎上，結合張睿[11]提出的復合LINEX對稱損失函數的方法，定義了復合MLINEX對稱損失函數，并在該損失函數下得到了對數伽瑪分布尺度參數的Bayes估計、E-Bayes估計、多層Bayes估計等。

本文在金秀巖[10]提出的復合MLINEX對稱損失函數的基礎上，研究兩參數Pareto分布的Bayes估計問題，在給定先驗分布為Gamma分布的基礎上給出Pareto分布參數的Bayes估計，并證明其容許性。最后在給定三類不同超參數先驗密度函數下，給出其E-Bayes估計和多層Bayes估計并對估計的性質進行研究。

1　參數θ的Bayes估計

定義1[1]：設X為隨機變量，若其分布函數為F(x)=為形狀參數，λ為尺度參數且為門限參數。則稱X服從兩參數θ，λ。則稱為Pareto分布，簡稱PD(θ,λ)。

設x1,x2,…,xn為來自PD(θ,λ)的獨立樣本，則其聯合密度為：

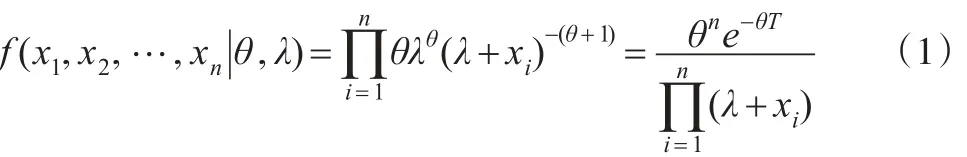
下頁圖1給出了在尺度參數λ=100時，形狀參數θ分別取0.5、1、2時的Pareto分布的密度函數圖像。由圖1可以看出Pareto分布的密度函數是單調遞減的函數。

定義2[11]：Mlinex非對稱損失函數定義為：

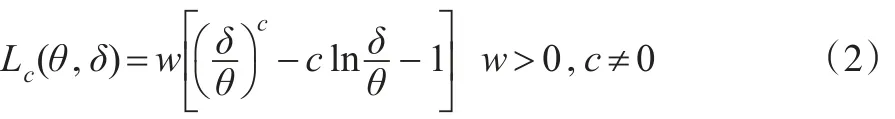
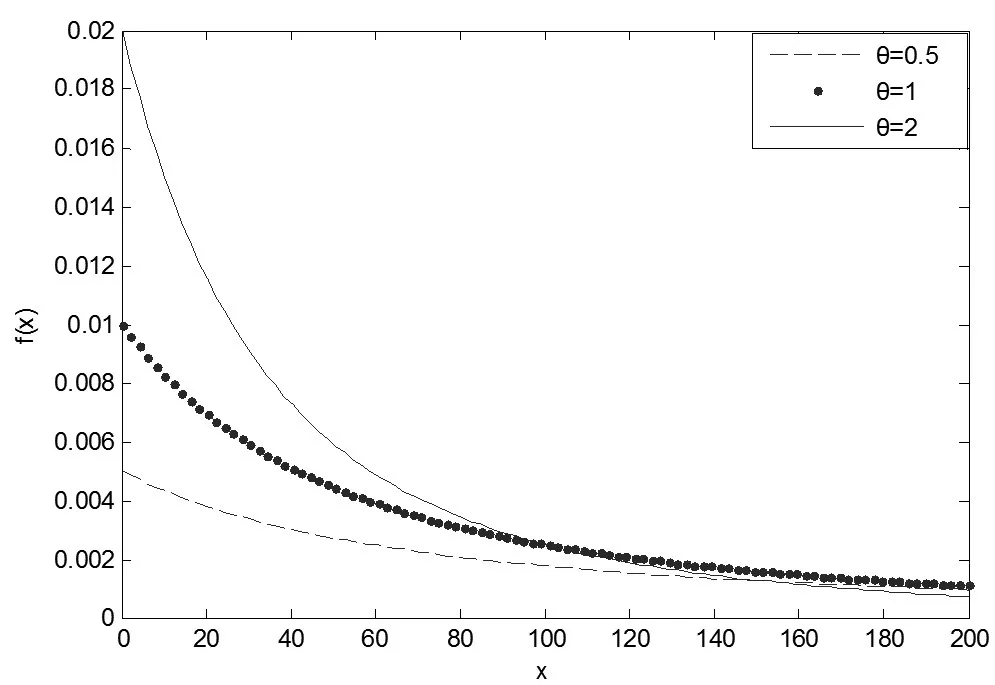
圖1Pareto分布的密度函數圖像（λ=100）

δ為參數θ的估計，c是一類非對稱損失函數。

定義3[10]：設損失函數Lc(θ,δ)由式（2）給出，則損失函數（3）稱為復合Mlinex對稱損失函數（見圖2），其中δ為參數θ的估計。

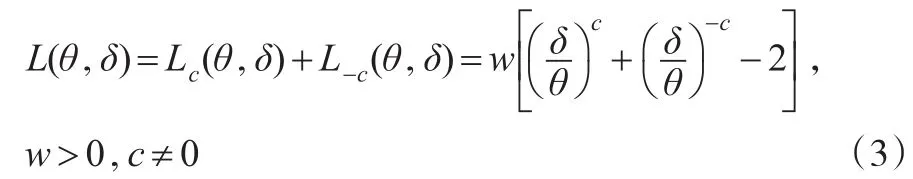
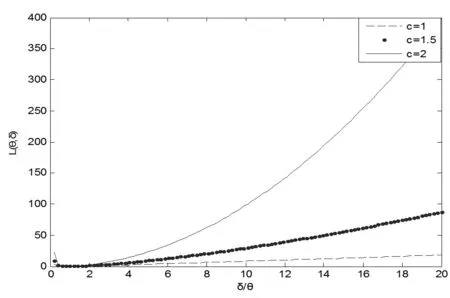
圖2復合MLINEX對稱損失函數圖像（w=1）

引理1：在損失函數（3）和模型f(x;θ,λ)=θλθ(λ+x)-(θ+1)下，若在空間中存在參數θ的估計量δ，其Bayes風險r(δ)＜+∞，則對于θ的任何先驗分布π(θ)，θ的唯一Bayes估計的一般形式為：

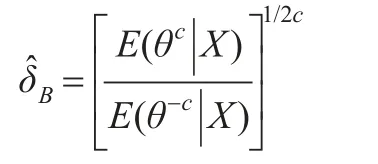
證明：具體證明與金秀巖在文獻[10]中的引理2.2的證明類似。

定理1：設x1,x2,…,xn是PD(θ,λ)的一組觀察值，形狀參數θ（尺度參數λ已知）的先驗分布π(θ)服從Gamma

證明：由題意知,形狀參數θ（尺度參數λ已知）的先驗分布π(θ)服從Gamma分布Γ(a,b)，則θ的密度函數為：

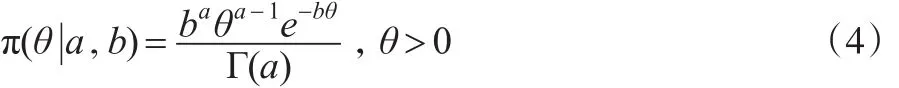
根據樣本聯合密度函數（1），并結合式（4），得到θ的后驗密度函數為：

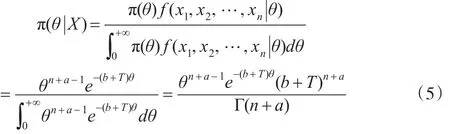
則θ的后驗分布密度服從以b+T為尺度參數，以n+a為形狀參數的Gamma分布。

由θ的唯一Bayes估計的一般形式及θ的后驗分布密度有：

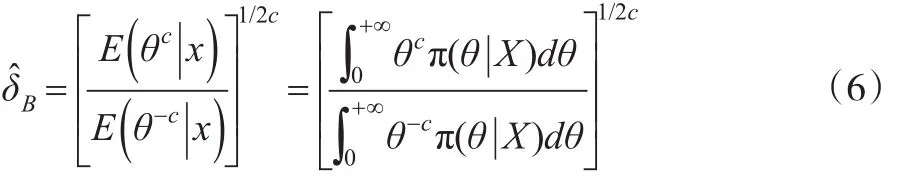
將式（5）代入到式（6）可得：

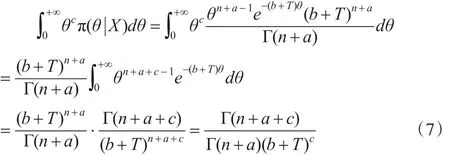
同理：

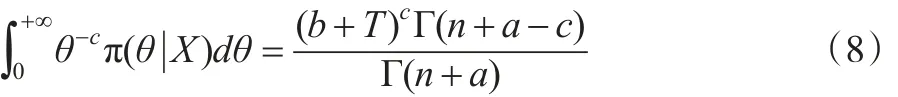
將式（7）和式（8）代入式（6），則：

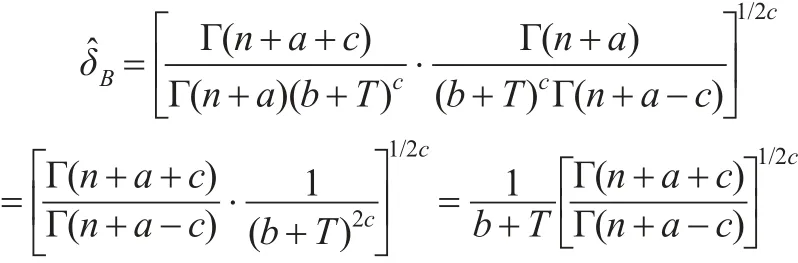
綜上所述，形狀參數θ的Bayes估計為：

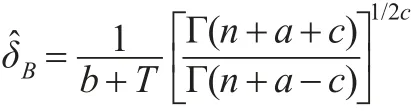
定理2：在給定先驗分布π(θ)和損失函數L(θ,δ)下，參數θ的Bayes估計是可容許的。

證明：對于Bayes估計的Bayes風險小于或者等于任何估計的Bayes風險，只需證明存在一個θ的一個估計δ，其Bayes風險r(δ)＜∞，于是可得r()＜∞，從而是可容許的。

由題意知：

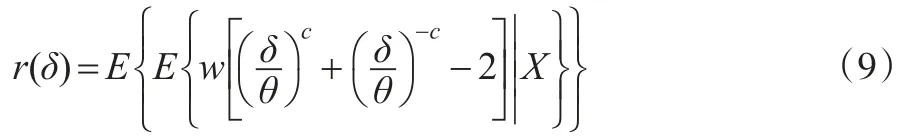
令δ=1，將其代入式（9），得到：

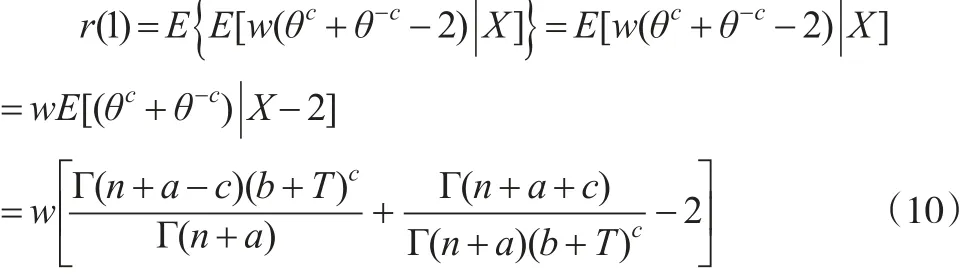
因為對于給定的樣本值，r(1)存在且有界，即r(1)＜∞。因此r(δ)＜∞。又因為r)＜r(δ)，則r()＜∞，故是可容許的。

2　參數θ的E-Bayes估計

下面引入形狀參數θ的E-Bayes估計的定義。

定義4[10]：對(a,b)∈D，若(a,b)是連續的，則稱參數θ的E-Bayes估計。存在的，D為超參數a和b取值的集合D={(a,b)|0＜a＜1,0＜b＜m,m＞0}，π(a,b)是a和b在集合D上的密度函數，(a,b)為參數θ的Bayes估計。

定理3：對于服從Pareto分布的樣本數據x1,x2,…,xn，若形狀參數θ服從Gamma分布，則θ的先驗密度

（1）若超參數a和b的先驗密度函數為：

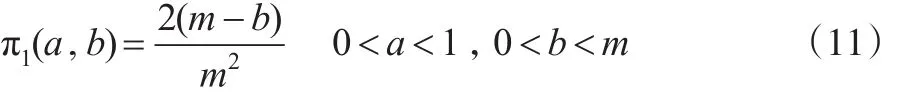
則參數θ的E-Bayes估計為：

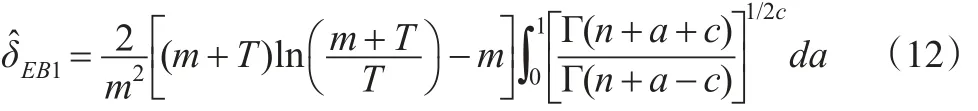
（2）若超參數a和b的先驗密度函數為：

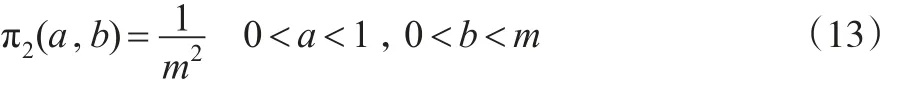
則參數θ的E-Bayes估計為：

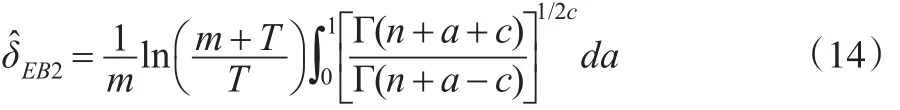
（3）若超參數a和b的先驗密度函數為：

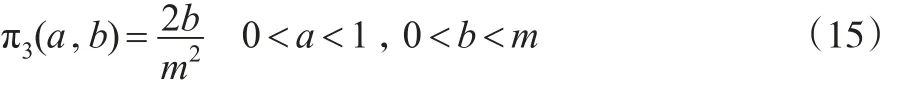
則參數θ的E-Bayes估計為：

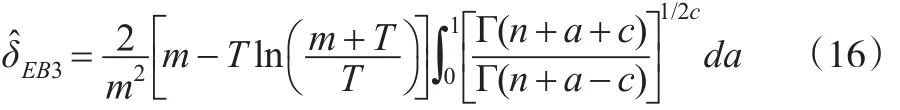
若超參數a和b的先驗密度函數π1(a,b)由式（11）給出，則參數θ的E-Bayes估計為：

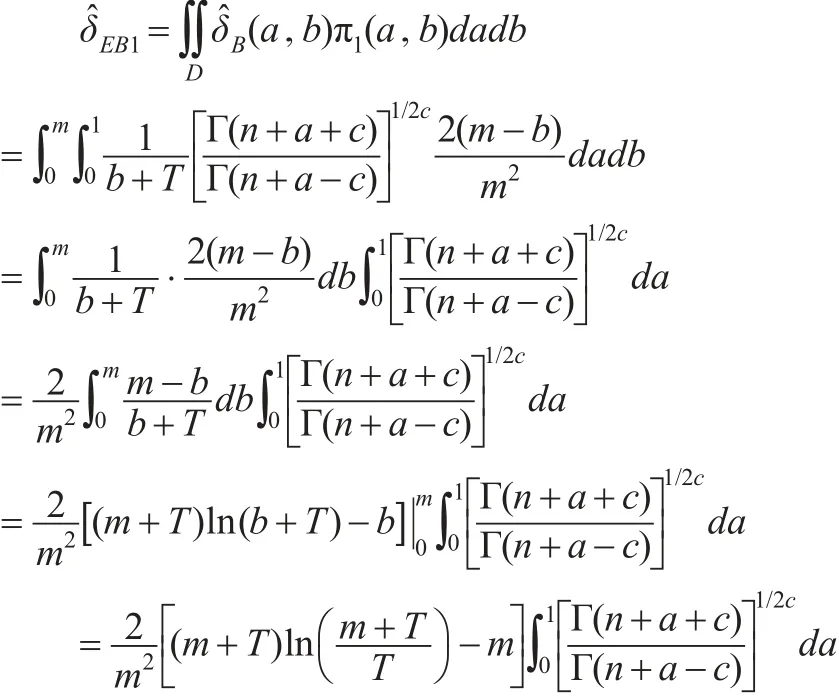
（2）同理，若超參數a和b的先驗密度函數π2(a,b)由式（13）給出，則參數θ的E-Bayes估計為：

（3）同理，若超參數a和b的先驗密度函數π3(a,b)由式（15）給出，則參數θ的E-Bayes估計為：

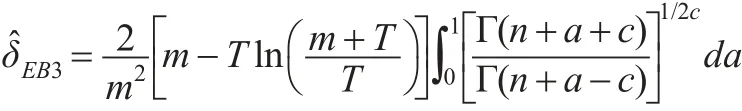
3　參數θ的多層Bayes估計

若形狀參數θ服從Gamma分布Γ(a,b)，則其先驗密度函數給定，那么如何確定超參數a和b？Lindley和Smith（1972）提出了多層先驗分布的想法，即在先驗分布中含有超參數時，可對超參數再給出一個先驗分布。

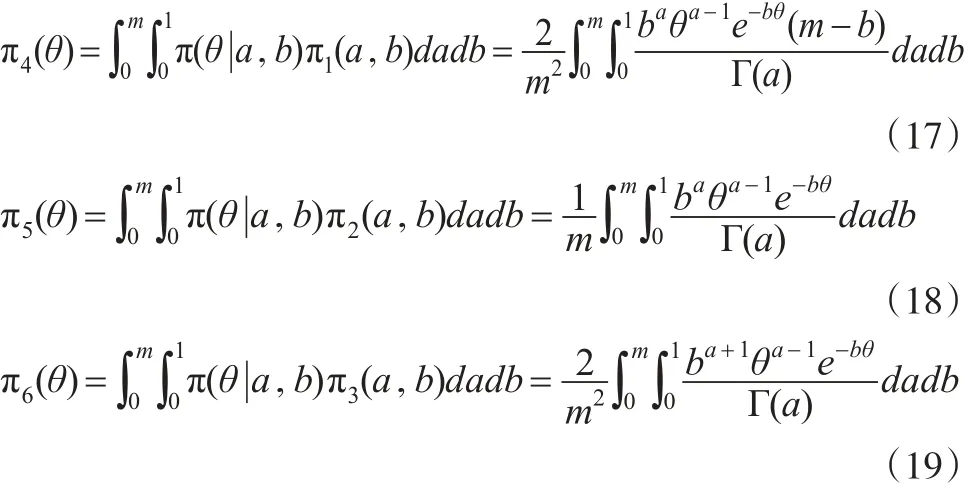
其中，0＜θ＜∞。

在以上三個不同的多層密度函數的基礎上，給出以下形狀參數θ的三個不同的多層Bayes估計。

定理4：對于Pareto分布下的樣本數據x1,x2,…,xn，若Pareto分布的形狀參數θ的多層先驗密度函數分別為式（17）至式（19），則在復合MLINEX損失函數下，θ的多層Bayes估計分別為：

證明：根據Bayes定理，則形狀參數θ的多層后驗密度函數為：

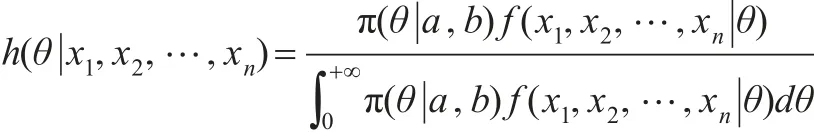
（1）當θ的多層先驗密度函數為式（17）時，θ的多層后驗密度函數為：

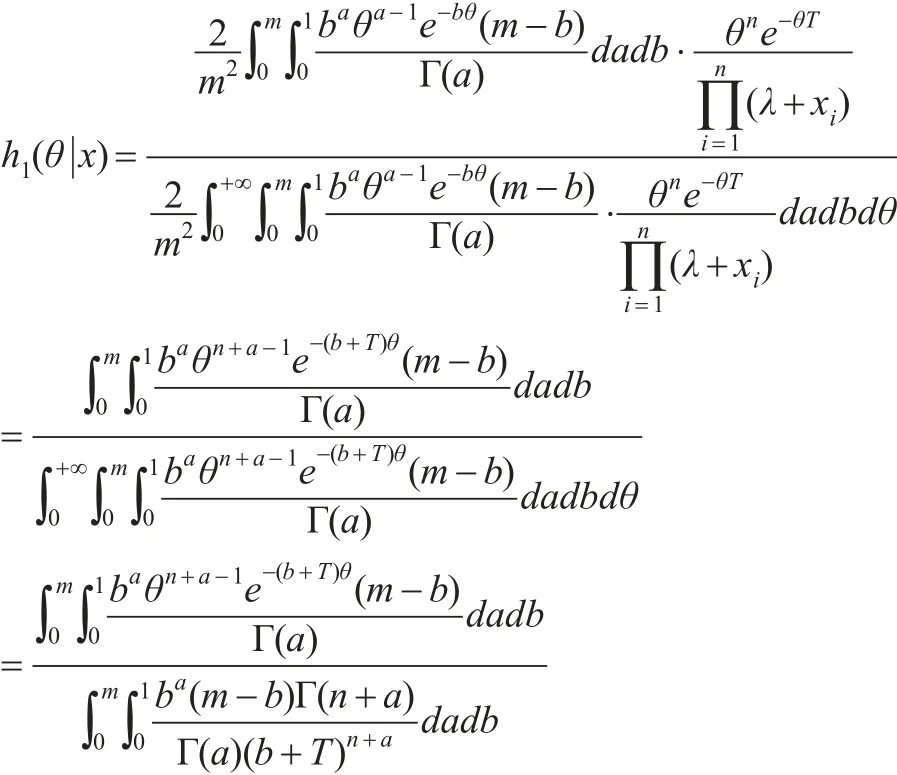
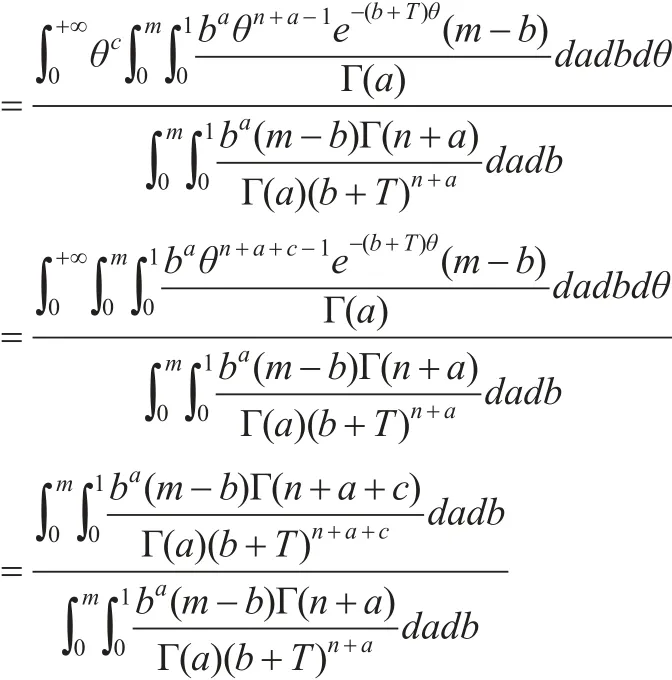
同理可得：

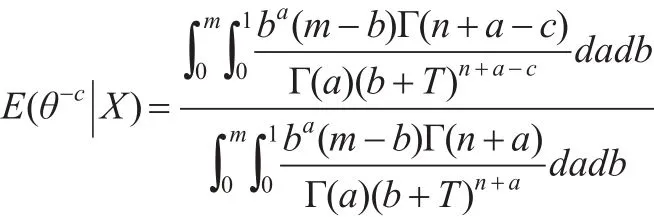
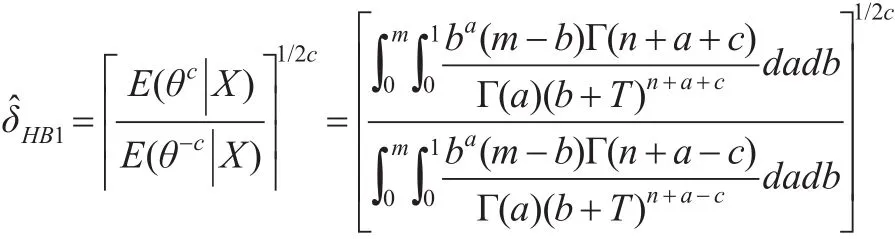
（2）同理，當θ的多層先驗密度函數為式（18）時，θ的多層后驗密度函數為：

結合定理1，此時形狀參數θ的多層Bayes估計為：

（3）同理當θ的多層先驗密度函數為式（19）時，θ的多層后驗密度函數為：

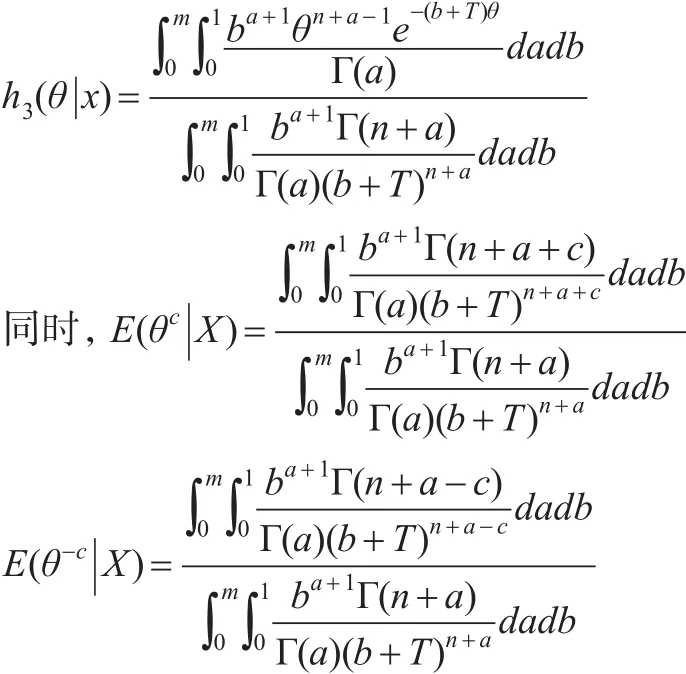
結合定理1，此時形狀參數θ的多層Bayes估計為：

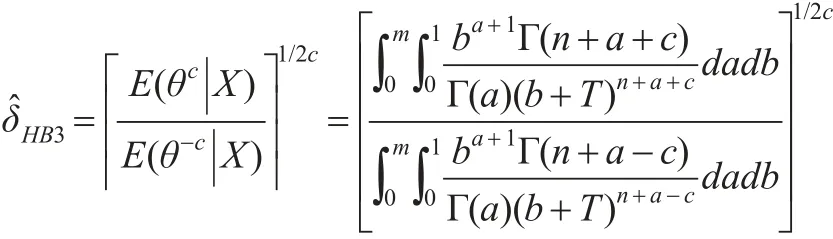
4　參數θ的E-Bayes估計的性質

定理5：在定理2中，當0＜m＜T時，有以下兩個結論：

證明：根據定理2，有：

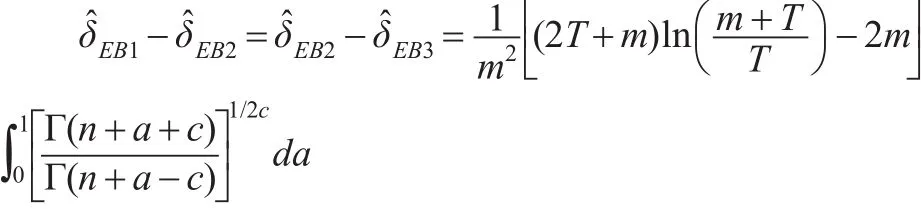
當-1＜x＜1時，根據泰勒展開式有：

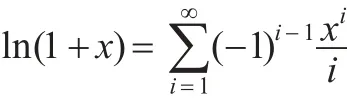
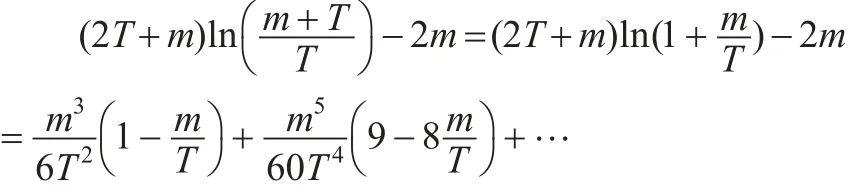
5　結束語

本文對Pareto分布在尺度參數為已知時,在MLINEX對稱損失下，分別給出了三種不同超參數的先驗密度函數下形狀參數E-Bayes估計（定理3）和多層Bayes估計（定理4），并驗證了形狀參數的三個不同E-Bayes估計具有保三者在T→∞時極限相等。

參考文獻：

[1]Pareto V.Cours Economic Politique[M].Lausanne and Paris:Rouge and Cie,1897.

[2]韓慧芳,楊珂玲,張建軍.Pareto分布中形狀參數的估計問題[J].統計與決策,2007，(24).

[3]韋程東,韋師,蘇韓.復合LINEX對稱損失下Pareto分布形狀參數的E-Bayes估計及應用[J].統計與決策,2009，(17).

[4]井曉培,周菊玲.廣義Pareto分布參數的經驗Bayes檢驗問題[J].數學的實踐與認識,2016，(5).

[5]沈新娣,丁幫俊.Pareto分布在逐步Ⅱ型區間刪失下的參數估計[J].應用概率統計,2016,32(2).

[6]韓明.Pareto分布形狀參數的E-Bayes估計和多層Bayes估計及其應用[J].純粹數學與應用數學,2016,32(3).

[7]Podder C K,Roy M K.Bayesian Estimation of the Parameter of Maxwell Distribution Under MLINEX Loss Function.[J].J.stat.stud,2003.

[8]Podder C K.Comparison of Two Risk Functions Using the Pareto Distribution[J].Pakistan Journal of Statistics,2004,20(3).

[9]任海平,李中恢.加權平方損失函數和MLINEX損失函數下一類分布族參數的Minimax估計[J].統計與決策,2009,(14).

[10]金秀巖.復合MLINEX對稱損失函數下對數伽瑪分布參數的Bayes估計[J].數學的實踐與認識,2014,(19).

[11]張睿.復合LINEX對稱損失下的參數估計[D].大連：大連理工大學碩士論文,2007.