自適應N-W核回歸估計量的改進

張穎

（濟南大學數學科學學院，濟南250022）

0　引言

在傳統的回歸分析中，往往假定回歸函數有某種特定的數學形式，一般是線性的或可轉化為線性的形式。回歸函數中包含若干個未知參數，并假定“隨機誤差項”服從正態分布。然而在實際問題中，不一定可以假定上述條件（回歸為線性、誤差為正態）成立，導致在實際應用中往往存在模型設計的誤差。由于現在越來越多的數據不適合用參數回歸來進行數據擬合，而非參數回歸是基于數據本身，所以非參數回歸越來越受到歡迎。自Stone（1977）[1]提出非參數回歸估計的權函數估計方法后，其方法引起了廣泛的重視。近幾十年來，權函數方法如核估計、局部多項式估計、近鄰估計等方法不斷發展完善，非參數回歸的理論和應用取得了較大的進展。在眾多非參數回歸方法中，核回歸估計是一種重要的、常用的估計方法，被廣泛應用于各種統計問題的研究中。核回歸估計具有分析簡單、便于實現等諸多優點，本文主要在N-W核回歸估計的基礎上研究了可變窗寬的自適應N-W核回歸估計，并提出了一種改進的自適應N-W核回歸估計。

1　N-W核回歸估計

顯然有

，g(x)=E(Y|X)=∫yf(x,y)dy，其中f(x,y)是fX(x)

(X,Y)的聯合密度函數，f(x)是的X邊緣密度函數。

回歸函數g(x)的估計量，記為：

核估計既與樣本有關，又與核函數k(?)及窗寬h有關。在給定樣本之后，一個核估計的性能就取決于核函數k(?)及窗寬h的選取。核函數k(?)的選擇并不是太重要，用不同的核所得到的估計在數值上非常類似。這個現象已經被理論上的計算所證實。這表明風險對于核的選擇是很不敏感的[2]。在實際應用中，經常使用的核函數有Epanechnikov核函數k(u)=(1-u2)(|u|≤1)和高斯核函數k(u)=核估計量的窗寬h影響著估計的光滑程度。若h選的過大，則估計過于平滑，會使某些特征（如多峰性）被淹沒，若h選的過小，整個估計特別是尾部就出現較大的干擾，從而又有增大方差的趨勢。因此窗寬h的選擇非常重要。最常使用的窗寬選擇方法主要有缺一交叉驗證法和插入法。其中，插入法主要基于核密度估計精度的測量——均方誤差分析中得來；缺一交叉驗證法（leave-one-out cross validation，簡稱CV）由Rudemo(1982)[3]和Bowman(1984)[4]從實際計算的角度提出。在缺一交叉驗證法中，通過最小化缺一交叉驗證函數CV(h)即可得到窗一交叉驗證函數一個leave-one-out核估計量。其定義由樣本容量為n-1的樣本{(X1,Y1),…,(Xi-1,Yi-1),(Xi+1,Yi+1),…,(Xn,Yn)}來估計g(Xi)。該方法直接由數據“自動”選擇窗寬。

2　自適應核密度函數估計

當n取定值時，缺一交叉驗證法得到的窗寬h是一個常數，即它既不依賴于位置x也不依賴于數據點Xi。選出的固定窗寬無法隨樣本觀測值的稀疏程度進行調整，這使得所得到的估計不能充分利用變量X的密度函數所提供的信息，估計結果會出現較大的誤差。另外，常數窗寬在待估回歸曲線具有復雜形狀時，缺乏靈活性。因此，理想中的窗寬選擇應該與樣本數據點的分散集中程度聯系起來。Breiman等(1977)[5]在密度函數估計的背景下提出了可變窗寬的概念。Abramson(1982)[6]和Silverman(1986)[7]分別對可變窗寬做了進一步的研究。

Silverman(1986)[7]通過使用右厚尾數據表明固定窗寬的核估計量X(x)和(x,y)并不適合厚尾分布，Silverman提出了密度函數的可變窗寬的核估計量，即密度函數的自適應核估計量。它允許窗寬變化，既可以對每個點x使用不同的窗寬，也可以對每個樣本數據點Xi使用不同的窗寬，這使得核密度估計更加靈活，更加適用于長尾密度函數的估計。因此，它是N-W核估計的改良和推廣。

在一元情形，在樣本點Xi處的具有可變窗寬的自適應核估計量定義為：

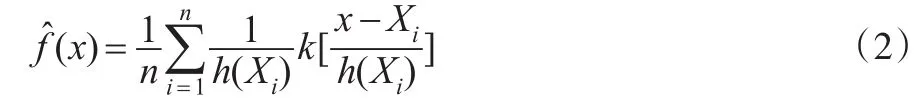
式（2）中的可變窗寬h(Xi)是一個依賴于Xi的可變窗寬，可變窗寬h(Xi)隨數據點Xi的變化而變化。可變窗寬的引入可以反映不同點的光滑程度，降低擬合曲線在峰頂區域的偏差以及尾部區域的方差，提高了擬合曲線的靈活性，適用于對復雜曲線的擬合。Abramson(1982)[6]在研究中提出h(Xi)與f(Xi成比例。在Abramson研究的基礎上，Silverman給出了自適應核密度估計的算法。

步驟2：定義局部窗寬因子λi={(Xi)g}-α，其中g(g≠0)為(Xi)的幾何平靈敏度參數，滿足0≤α≤1。

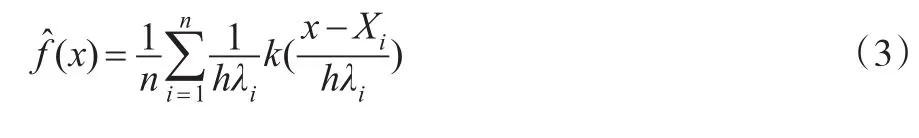
從式（3）可以看出，自適應窗寬h(Xi)=hλi。當靈敏度參數α=0時，自適應核密度估計與固定窗寬的核密度估計相等；當α=1時，自適應核密度估計與近鄰核估計相等。Abramson和Silverman的研究表明，在實際應用中，當α=0.5時，自適應核密度估計效果最好。

利用乘積核函數，同時使用可變窗寬代替固定窗寬，Sain(1994)[8]給出r元密度函數的自適應核密度估計的二元聯合密度函數的核密度估計定義為(x,y)=

3　自適應N-W核回歸估計

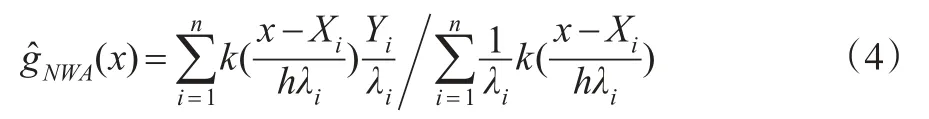
證明：

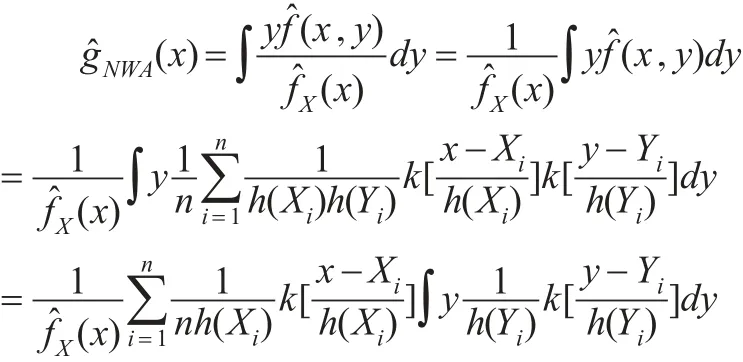
利用核函數的性質1和性質2，就可以得到自適應NW核回歸估計量：

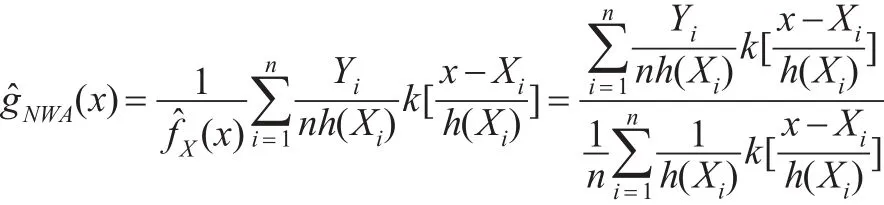
取可變窗寬h(Xi)=λih，則自適應N-W核回歸估計量

公式（4）中的局部窗寬因子λi可由Silverman關于自適應密度函數估計的算法得到。在計算局部窗寬因子λi可得到一個改進的自適應N-W核回歸估計量

本文將通過模擬研究來比較N-W核估計量（NW）、自適應N-W核估計量（ANW）、改進的自適應N-W核估計量（A*NW）三者的估計效果。

4　模擬

為了比較文中所提到的三種核回歸估計量的估計效果，本文利用以下兩個模型分別模擬容量為200的兩個樣本來做模擬研究。

模型1：Y=Xsin2πX+ε，其中ε～N(0,0.1),X～U[0,1]。

模型2：Y=cos2πX+ε，其中ε～N(0,0.1),X～U[0,1]。

采用Epanechnikov核函數，真實回歸函數曲線g(x)和由三種核估計量得到的擬合曲線如圖1和圖2所示。

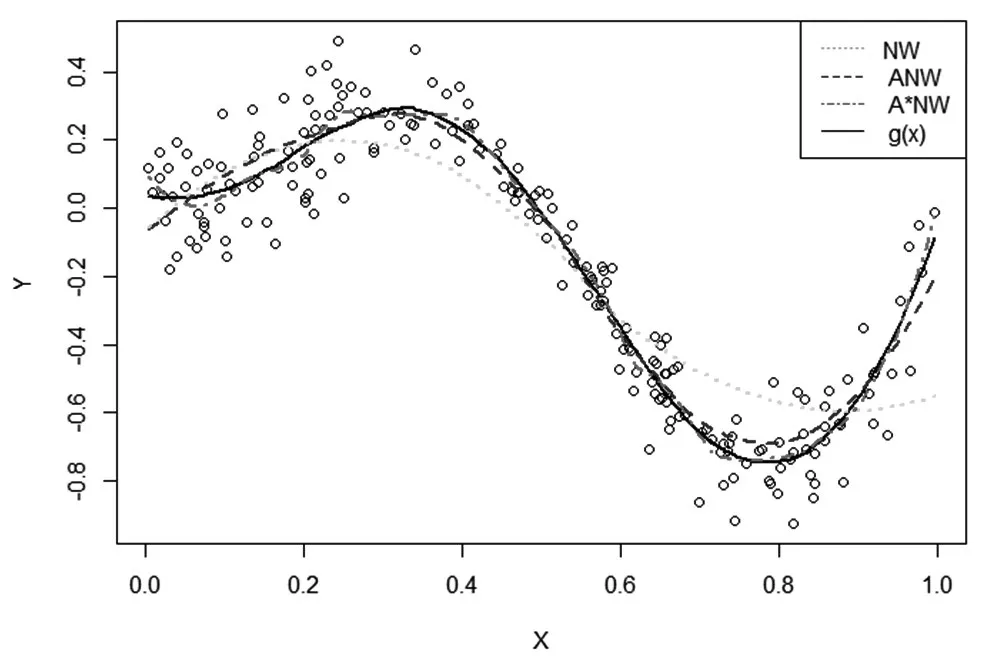
圖1模型1的核估計回歸曲線

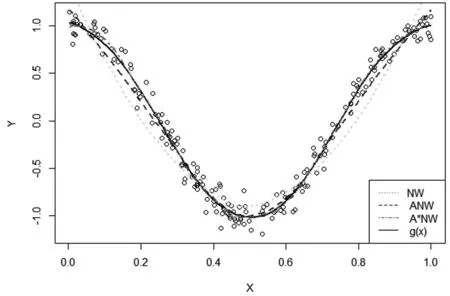
圖2模型2的核估計回歸曲線

使用擬合優度和均方誤差（MSE）來評價三種估計量的估計效果在兩種模型下，分別計算出三種核回歸估計量的MSE值，計算結果見表1。

表1　利用Epanechnikov核函數得到的核估計量的擬合優度和均方誤差

從表1可以看出，在兩種模型下，采用Epanechnikov核函數，可變窗寬的自適應N-W核回歸估計量的MSE值都比固定窗寬的N-W核回歸估計量的MSE值小，特別是改進的自適應N-W核回歸估計量的MSE值都是最小的，這說明文中所提出的方法同N-W核估計、自適應N-W核估計相比，優越性更加明顯。

5　實例

研究加拿大工人收入（income）和年齡（age）的關系，該數據來源于R程序包“SemiPar”，樣本觀測值為205，解釋變量為age，被解釋變量為log.income(log.income=log(income))。本文分別應用N-W核回歸估計量和兩種自適應N-W核回歸估計量來擬合age與log.income之間的函數關系。圖3是采用Epanechnikov核函數計算出的三種N-W核回歸估計量得到的回歸擬合曲線。

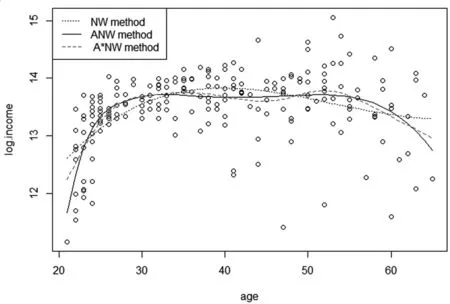
圖3利用Epanechnikov核函數得到的核估計回歸曲線

由圖3可以看出，從整體擬合效果上觀察，文中提出的改進的自適應N-W核估計方法優于其他兩種估計方法，而自適應N-W核回歸方法優于N-W核回歸估計方法，同時發現可變窗寬的自適應N-W核回歸估計明顯優于固定窗寬的N-W核回歸估計，特別是在稀疏樣本點和邊界點處，表現得更為明顯。使用固定窗寬的N-W核回歸分析方法擬合時，邊界點的估計偏差較大，即存在邊界效應，而用可變窗寬的自適應N-W核回歸分析方法卻能很好地減少邊界效應。通過實例，進一步驗證了模擬研究中的結論。

6　結論

為了更好地估計回歸函數，本文對自適應N-W核回歸估計進行了研究。模擬研究結果表明，具有可變窗寬的自適應N-W核回歸估計比固定窗寬的N-W核回歸估計的估計效果更好，對于一個自適應N-W核回歸估計量來說，使用算術均值得到的窗寬比使用幾何均值得到的窗寬在估計效果上有更大的優勢。總之，本文所用的可變窗寬核回歸方法，繼承了核回歸的優點，并且使用可變窗寬提高了估計的效果，并使之能成功地處理復雜形狀的曲線的擬合問題。

參考文獻：

[1]Stone C J.Consistent Nonparametric Regression[J].Annals of Statistics,1977,5(4).

[2]Brown L D,Zhang C H.Asymptotic Equivalence Theory for Nonparametric Regression With Random Design[J].Annals of Statistics,2003,30(3).

[3]Rudemo M.Empirical Choice of Histograms and Kernel Density Estimation[J].Scandinavian Journal of Statistcs,1982,(9).

[4]Bowman A W.An Alternative Method of Cross-validation for the Smoothing of Density Estimates[J].Biometrika,1984,71(2)．

[5]Breiman L,Meisel W,Purcell E.Variable Kernel Estimates of Multivate Densities[J].Technometrics,1977,(19).

[6]Abramson I S.On Bandwidth Variation in Kernel Estimates-A Square Root Law[J].Annals of Statistics,1982,10(4).

[7]Silverman B W.Density Estimation for Statistics and Data Analysis[M].London:Chapman&Hall,1986.

[8]Sain S R.Adaptive Kernel Density Estimation[D].Texas:Rice University,1994.