基于灰度極限學習機的糧食產量預測
樊 超, 曹培格, 郭亞菲, 楊鐵軍
(河南工業大學信息科學與工程學院,河南鄭州 450001)
無糧則不穩,糧食生產是糧食安全的基石,不僅關系國計民生,而且直接影響社會穩定和經濟發展。雖然我國目前已經基本實現了糧食總量平衡、年年有余的目標,但仍面臨著人口多、耕地少且可耕地面積日益萎縮的狀況,嚴重影響國家的糧食安全。為此,研究糧食產量的變化規律并對其發展趨勢作出準確預測,對于保障國家糧食安全、指導政府部門制定科學的發展規劃和政策具有重要意義。
由于糧食生產受社會、經濟、氣候等多種因素的影響,導致糧食產量預測成為復雜的農學和統計學問題。為準確預測糧食產量,目前普遍采用遙感技術預測模型[1]、統計動力學生長模型[2]、氣象產量預測模型[3]以及基于自回歸滑動平均模型(auto-regressive and moving average model,簡稱ARMA模型)和灰度理論等的時間序列預測等方法[4-7]。這些方法雖然在一定程度上能夠對糧食產量作出預測,但均不同程度地存在所需數據量大、預測成本高以及預測精度不理想等缺點。
由于糧食生產受到多種顯性和隱性因素的影響,具有明顯的灰度特征,因此可以使用灰色模型預測糧食產量。傳統的灰色模型能有效地預測少量數據序列,但隨著數據的增多和波動性的增大,該模型逐漸失去它的優勢[8]。而極限學習機較適用于對大樣本數據進行預測,一般情況下,訓練數據越多,對樣本數據規律擬合得越好,預測誤差越小。為此,本研究結合糧食產量的數據特點,將灰色預測算法和極限學習機算法相結合,提出基于灰色極限學習機的糧食產量短期準確預測模型。
1 灰色預測模型
灰色預測模型的基本原理是對雜亂無章的原始數據列進行累加,生成新的單調遞增數據列,增加原始數據列的規律性,弱化其波動性;按照累加后序列的增長趨勢建立預測模型,得到1組單調遞增數據序列;然后對預測數據采用累減的方法進行逆運算,恢復原時間序列,得到預測結果。其中 GM(1,1) 是目前灰色模型中使用最廣泛的模型,其建模步驟如下。
(1)生成累加序列。設原始時間序列X(0)包含n個非負元素,即:
X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]。
(1)
由該序列生成一次累加序列X(1),
X(1)=[x(1)(1),x(1)(2),…,x(1)(n)]。
(2)
其中
(3)
式中:x(0)(r)指原始時間序列中的第r個元素。
(2)生成累加序列X(1)的緊鄰均值序列Z(1):
Z(1)=[z(1)(1),z(1)(2),…,z(1)(n)]。
(4)
這里:
(5)
(3)構建累加序列X(1)對時間t的一階微分方程:
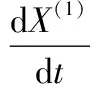
(6)
式中:參數a、b可由式(7)計算得出。
[a,b]T=(BTB)-1BTY。
(7)
式中:
(8)
(4)求解微分方程,得到如下GM(1,1)模型:
(9)
(5)由累加序列還原原序列:
(10)
2 極限學習機預測算法

(11)
式中:wi為輸入神經元與第i個隱含層節點的連接權值;βi為第i個隱含層節點與輸出神經元的輸出權值;bi為第i個隱含層節點的偏置;tp為第p個輸入樣本的輸出值。式(11)等價于:
Hβ=T。
(12)
式中:
(13)
(14)
式中:T為網絡輸出矩陣;H為極限學習機的隱含層輸出矩陣,其第i列為第i個隱層節點的輸出向量,該向量與輸入值x1、x2,…,xN有關。因此,對于一個含有M個輸入節點、L個隱層節點,且激勵函數為g(x)的標準極限學習機,其算法過程可包括如下3步:(1)隨機設置輸入權值ωi和偏置bi,1≤i≤L;(2)計算隱層輸出矩陣H;(3)計算輸出權值β=H+T,其中H+為H的Moor-Penrose(MP)廣義逆。

從上述過程可以看出,ELM算法可隨機產生輸入層和隱含層的連接權值ωi及隱含層神經元的偏置bi,且在訓練過程中無需調整,只須選定激勵函數、設定隱層節點個數,即可得到唯一的最優解。因此,ELM算法具有學習速度快、泛化性能好等優點。
3 灰色極限學習機組合預測算法
灰色極限學習機預測算法主要由灰色預測算法和極限學習機算法等2個預測模型組合而成。灰色預測模型適用于小樣本的數據預測,在大樣本的數據預測問題上,效果較差,但可以選取距離待預測年份較近的少量樣本數據進行建模;而極限學習機通常適用于大樣本的數據預測,且訓練數據越多,模型對樣本數據規律的擬合性越好,能夠較全面地反映數據序列的變化規律。因此,灰色極限學習機預測算法可通過使用不同的樣本集分別構建灰色預測模型和極限學習機模型,然后根據2個模型對數據序列的預測效果進行加權,克服單一預測方法的不足,從而得到較為準確的預測結果。
假設時間數據序列含有N個數據元素,記為X=[x1,x2,…,xN],且數據序號越大(即在序列中越靠后)的元素其時間點越靠后,距離待預測數據時間越近。灰色極限學習機算法步驟可描述為:

(2)計算灰色模型擬合誤差序列Eg:
(15)
(3)計算灰色模型權值qg。在預測領域中,距離預測時間點越近,數據的預測誤差越重要。因此,基于該思想的合理性,權值計算公式為
qg=|εN|+r|εN-1|+…+rN-l+1|εN-l+1|。
(16)
式中:r為權值因子,0≤r<1。

(17)
(18)
(5)計算極限學習機模型的擬合誤差序列Eε:
(19)
(6)計算極限學習機模型權值qε。具體計算公式為
qε=|εN-j-1|+r|εN-j-2|+…+rN-j-2|ε1|。
(20)
式中:r為權值因子,0≤r<1。
(7)分別使用步驟(1)、步驟(4)所建立的灰色預測模型和極限學習機模型對序列X進行預測,得到預測序列Yg和Yε。
(8)使用步驟(7)并結合步驟(3)、步驟(6)得到的權值qg、qε以及最終預測序列Y。
(21)
綜上所述,灰色極限學習機預測模型的算法步驟如圖2所示。

4 基于灰色極限學習機的糧食產量預測
為驗證基于灰色極限學習機組合模型的糧食預測效果,選取1949—2013年我國的糧食產量數據作為研究對象,構成原始時間序列X。為方便驗證模型,將該序列中1949—2010年的數據作為訓練子序列X1,2011—2013年的數據作為預測子序列X2。首先從訓練子序列X1中挑選2000—2010年共11個元素構成新的時間序列,使用灰度建模方法建立該序列的GM(1,1)模型,利用該模型對2011—2013年糧食產量數據進行預測,預測結果如表1所示。其次,對訓練集樣本X1進行數據歸一化處理,處理公式為:
X1′(i)=[max(X1)-X1(i)]/[max(X1)-min(X1)]。
(22)
式中:X1為原序列;X1′為歸一化后的序列;X1(i)、X1′(i)分別為序列X1、X1′的第i個元素。選取極限學習機的滯后階數為5(即極限學習機的輸入節點數為5),構建結構為5-11-1的極限學習機預測模型,其中學習機的激勵函數為Sigmoid函數。利用訓練好的網絡模型對2011—2013年的糧食產量進行預測,通過反歸一化處理得到的預測數據見表1。分別計算灰度模型和極限學習機模型的擬合誤差,選取權值因子r=0.9,根據公式(16)、公式(20)分別計算灰度模型、極限學習機模型的權重系數qg/(qg+qε)=0.48、qε/(qg+qε)=0.52。然后根據公式(21)得到基于灰色極限學習機組合模型2011—2013年的糧食產量。
從表1可以看出,由于2011年距離訓練集樣本最近,因此,使用GM(1,1)模型得到的預測產量最精確,但GM(1,1)模型建模時所用數據元素較少,隨著時間的增加,預測誤差明顯增大。而極限學習機方法結合了較多產量數據的歷史信息,使得預測誤差總體較為平穩。由于灰度極限學習機算法結合了灰度模型和極限學習機模型各自的優勢,使得其產量預測效果較好,2012、2013年的糧食產量預測誤差明顯小于其他2種方法。3種方法3年的平均預測誤差分別為2.65%(極限學習機)、3.25%(灰度模型)、1.19%(灰度極限學習機模型),由此可見,灰度極限學習機模型可以準確預測未來3年的糧食產量數據。
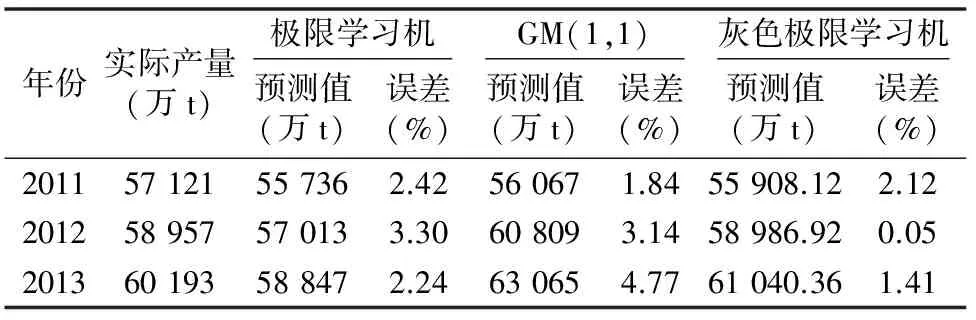
表1 各種模型得到的糧食產量數據
5 結論
糧食安全是關系國民經濟健康發展和全面建設小康社會的重大問題,因此對糧食產量的短期、精確預測對于保障國家糧食安全和協助糧食管理部門作出科學有效決策具有重大意義。本研究根據糧食產量數據灰度性特點,將灰色模型的小樣本短期預測功能和極限學習機大樣本規律預測功能相結合,采用灰度極限學習機組合模型對糧食產量進行短期預測。對2011—2013年糧食產量的預測結果表明,該組合方法能夠準確預測未來3年的糧食產量,平均預測誤差約為1.19%,為糧食產量的短期精準預測提供了新的技術手段。
參考文獻:
[1]譚昌偉,羅明,楊昕,等. 運用PLS算法由HJ-1A/1B遙感影像估測區域冬小麥理論產量[J]. 中國農業科學,2015,48(20):4033-4041.
[2]張虹. 基于系統動力學的我國糧食安全問題研究[D]. 成都:成都理工大學,2009.
[3]劉春瓊,劉萍,吳生虎,等. 基于DCCA方法分析氣候變化對四川省糧食產量的影響[J]. 中國農業氣象,2016,37(1):43-50.
[4]范成方,史建民. 基于Holt-Winters及趨勢-ARMA組合模型的糧食種植成本預測分析——以山東省玉米、小麥為例[J]. 中國農業資源與區劃,2014,35(3):45-51.
[5]張超,何翔宇,吳榮濤,等. 基于等維新息GM(1,1)模型的河南省糧食產量預測[J]. 河南農業大學學報,2015,49(4):556-560,572.
[6]禹建麗,黎婭. 基于人工神經網絡的糧食產量預測模型[J]. 河南農業科學,2005(7):44-46.
[7]楊雨時,董連杰,管琳. 基于粗糙集理論和BP神經網絡的糧食產量預測方法[J]. 農機化研究,2014(11):34-37.
[8]楊克磊,張振宇,和美. 應用灰色GM(1,1)模型的糧食產量預測研究[J]. 重慶理工大學學報(自然科學),2015,29(4):124-127.
[9]Huang G B,Zhu Q Y,Siew CK. Extreme learning machine:a new learning scheme of feedforward neural networks[C]//2004 IEEE International Joint Conference on Neural Networks. Hungary:Budapest,2004.

