引入虛擬節點的無線傳感器網絡ELM定位算法*

劉國繁， 趙天霓

(1.湖南工程學院 電氣信息學院，湖南 湘潭 411104；2.湘潭大學 信息工程學院，湖南 湘潭 411105)

0 引 言

無線傳感器網絡節點自身位置信息的獲取是大多數應用的基礎，節點定位技術是無線傳感器網絡的關鍵支撐技術。依據是否測量距離，定位算法可劃分為基于測距的算法和非測距的算法[1]。前者[2]對距離進行直接測量，通常定位精度相對較高，但節點需要額外硬件的支持，并且定位過程會消耗大量的能量。非測距算法[3]則依靠網絡連通度等信息即可計算未知節點的位置，對節點的硬件要求小。

反向傳播(back propagation,BP)定位算法是將BP神經網絡用于節點定位的一類算法，但傳統BP神經網絡需要人為設置大量訓練參數，存在訓練速度慢并且容易陷入局部最優解等問題。極限學習機(extreme learning machine，ELM)的輸入權值和隱含層閾值均隨機產生，僅需要設置網絡的隱含層節點個數，即可產生唯一最優解，并且無需迭代，因而學習速度快，具有良好的泛化性能[4～6]。將ELM應用于節點定位可有效避免BP定位算法存在的問題，改善定位性能。

現有的定位算法均表明，錨節點比例越高，定位的精度越高[3]，但是錨節點的增多會使無線傳感器網絡的成本增加。引入虛擬節點[7～9]及次錨節點[10,11]等于虛擬地增加錨節點比例，在不增加硬件成本情況下，提高了無線傳感器網絡節點定位精度。本文將ELM用于無線傳感器網絡的節點定位，引入虛擬節點進一步提高定位精度，仿真結果表明：使用ELM定位具有較小的定位誤差，且結合虛擬節點可進一步減小定位誤差。

1 基于ELM的定位算法

1.1 ELM

對于N個樣本數組(xi,ti),xi=[xi1,xi2,...,xin]T∈Rn,ti=[ti1,ti2,...,tim]T∈Rm,隱含層節點數為L，激活函數為g(x),ELM模型可表示為

(1)

式中wj=[wj1,wj2,…,wjn]T為連接輸入節點與第j個隱含層節點的權值向量；βj為連接第j個隱含層節點與輸出節點間的權值向量；bj為第j個隱含層節點的閾值；g(wjxi+bj)是在輸入為xi時第j個隱含層節點的輸出。SLFNs模型能以零誤差逼近這N個樣本，上述N個等式可以寫為

(2)

式中H為隱含層輸出矩陣，H的第i列為第i個隱含層的節點對應于輸入x1,x2,…,xN的輸出。求解式(2)，可以得到網絡參數為

β=H*T=(HTH)-1HTT

(3)

式中H*為隱含層輸出矩陣H的Moore-Penrose廣義逆。

1.2 最小跳數獲取

每個錨節點將自己的位置坐標、自身ID信息、跳數(初值為0) 作為一個數據包發送給通信半徑內的鄰居節點。鄰居節點接收數據包后,記錄下到錨節點的跳數,當接收到來自同一個錨節點的多個跳數信息時，刪除較大的跳數信息，保存最小的跳數信息，跳數值加1繼續轉發至鄰居節點。網絡中的所有節點(包括錨節點)記錄了距每個錨節點間的最小跳數。

1.3 ELM估算節點位置

設Si=(xi,yi)表示第i個節點的坐標(位置)。Bi=[bi1,bi2,…,bim,…,biM]為各個錨節點間的最小跳數，bim為第i個錨節點與第m個錨節點間最小跳數，i=1,2,…,M，m=1,2,…,M，當i=m，有bim=0。Bj=[bj1,bj2,…,bjm,…,bjM]為各未知節點到各錨節點之間的最小跳數，bjm為第j個未知節點與第m個錨節點間最小跳數，j=M+1,M+2,…,N，m=1,2,…,M。則估算步驟為：

1)無線傳感器網絡中隨機放置N個節點，其中前M個為錨節點，剩余N-M個為未知節點。錨節點向周圍鄰居節點發送坐標、ID、跳數信息，網絡中所有節點記錄下最小跳數信息。

2)建立各節點與錨節點間最小跳數與對應節點位置的ELM關系模型。以各節點與錨節點間最小跳數為輸入，對應節點位置為輸出，將實驗數據劃分為訓練集和測試集。

3)將Bi=[bi1,bi2,…，bim，…,biM]作為訓練集的輸入，對應錨節點的位置Si=(xi,yi)為訓練集的輸出，i=1,2,…,M，m=1,2,…,M，對ELM算法進行訓練，保存訓練獲得的參數H和β。

4)將Bj=[bj1,bj2,…,bjm,…,bjM]作為測試集，測試結果為對應未知節點的位置Sj=(xj,yj)。輸入測試集，獲取測試結果并分析。

2 引入虛擬節點的ELM定位算法

2.1 次錨節點

文獻[8]將一部分未知節點升級為次錨節點實現了未知節點的定位問題。即網絡部署階段的部分未知節點，在定位過程得到較為精確的位置信息，升級為次錨節點，進一步對未知節點進行定位。節約了網絡成本并且使網絡定位精度得到了有效提高。

次錨節點的選擇，是在對未知節點進行定位后，從中選出定位精度較為準確的未知節點升級為次錨節點。次錨節點的位置信息是未知節點定位后得到的估計位置，由于未知節點的實際位置是未知的，從而無法判斷未知節點的實際位置與估計位置的誤差。本文使用虛擬節點來解決這一問題，在所有未知節點中選出定位誤差相對較小的未知節點作為次錨節點。

2.2 虛擬節點定位

虛擬節點沒有節點間的通信和信息交互能力，不能直接獲取虛擬節點到各錨節點之間的最小跳數，但是可以將距離轉化為跳數。假設虛擬節點的位置已知，可先求出虛擬節點與錨節點間距離，再將距離信息轉化為跳數信息。

如圖1，節點O為錨節點，節點A和B為虛擬節點，O的通信半徑為R，可知虛擬節點A和錨節點O之間距離DOAR，則虛擬節點B和錨節點之間距離大于一跳，B和O的最小跳數要綜合考慮B和周圍鄰居節點的跳數信息確定。

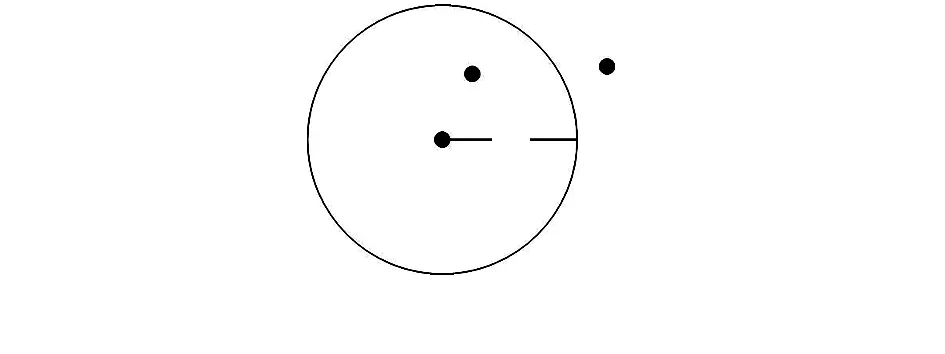
圖1 跳數分析

獲取虛擬節點與各錨節點之間最小跳數信息后，用訓練好的ELM估計虛擬節點的位置信息。

2.3 次錨節點的選取

將虛擬節點估計位置與實際位置進行比較，選出誤差足夠小的虛擬節點，刪除其余的虛擬節點，并記錄虛擬節點到各錨節點的最小跳數。

為了確定次錨節點，設到所有錨節點最小跳數相同的點位置相近。篩選出虛擬節點到各錨節點最小跳數與到各錨節點最小跳數相同的未知節點，其坐標即對應虛擬節點坐標，將之升級為次錨節點。

2.4 引入虛擬節點的ELM定位算法流程

1)隨機放置N個節點，其中前M個為錨節點，剩余N-M個未知節點。錨節點向周圍鄰居節點發送坐標、ID、跳數信息，網絡中所有節點記錄下最小跳數信息。Si=(xi,yi)表示第i個節點的坐標(位置)。Bi=[bi1,bi2…bim…,biM]為各個錨節點間的最小跳數。Bj=[bj1,bj2,…bjm…,bjM]為各未知節點到各錨節點之間的最小跳數。

2)建立各節點與錨節點間最小跳數與對應節點位置的ELM關系模型。以各節點與錨節點間最小跳數為輸入，對應節點位置為輸出，將實驗數據劃分為訓練集和測試集。

3)將Bi作為訓練集的輸入，對應錨節點的位置Si為訓練集的輸出。對ELM算法進行訓練，保存訓練獲得的參數H和β。

4)在網絡中設置C個虛擬節點，其位置表示為Tp=(xp,yp)，將虛擬節點與錨節點間距離轉化為跳數。各虛擬節點到各錨節點之間的最小跳數Bp=[bp1,bp2,…,bpm,…,bpM]，bpm為第p個虛擬節點與第m個錨節點間最小跳數，p=1,2,…,C，m=1,2,…,M。

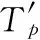
6)篩選出Bj=[bj1,bj2,…,bjm,…,bjM]與Bq=[bq1,bq2,…bqm,…,bqM]相同的未知節點，將這P個未知節點確定為次錨節點，P≤D。

7)將次錨節點和錨節點均作為無線傳感器網絡的錨節點為其余未知節點提供定位信息。此時網絡中錨節點個數為M+P個，未知節點N-M-P個。

8)重新構建各節點與錨節點間最小跳數與對應節點位置的ELM關系模型。以Bi=[bi1,bi2,…,bim,…,bi(M+P)]，i=1,2…,M+P，m=1,2,…,M+P，為訓練集的輸入，對應錨節點的位置Si=(xi,yi)為訓練集的輸出訓練ELM。

9)令Bj=[bj1,bj2,…,bjm,…,bjM]為測試集，測試結果為對應未知節點的位置Sj=(xj,yj)，j=M+P+1,M+2,…,N，m=1,2,…,M+P。輸入測試集，獲取測試結果并分析。

3 仿真分析

為驗證所述方法的性能，對傳統基于距離矢量跳(distance vector-based hop,DV-Hop)定位算法，BP定位算法改進的加權質心定位算法基于次級錨節點(improved weighted centroid localization algorithm for WSNs based on secondary anchor nodes,，IWCLA-SAN)算法[11]，ELM定位算法，以及引入虛擬節點的ELM算法分別在MATLAB平臺上進行仿真。設所有節點均隨機分布在100 m×100 m的區域內，每組不同條件的均仿真運行100次，對結果取平均值進行分析比較。

3.1 錨節點比例對定位誤差的影響

對不同的錨節點比例進行仿真對比，共隨機分布200個節點，通信半徑設為40 m，其如圖2所示。仿真結果中每種算法的定位誤差均隨錨節點所占比例的提升而減小。在錨節點比例小于10 %時，IWCLA-SAN算法誤差最小。但在錨節點比例大于等于10 %的情況下，引入虛擬節點的ELM定位算法較IWCLA-SAN，BP算法及DV-Hop算法誤差小。引入虛擬節點的ELM算法較ELM算法定位誤差平均下降了3.76 %，說明在錨節點所占比例不同的情況下，引入虛擬節點升級次錨節點對于降低節點定位誤差有效。

圖2 錨節點所占比例和定位誤差關系

3.2 對定位誤差影響

對不同通信半徑進行仿真，仿真中共隨機分布200個節點，錨節點比例為10 %，仿真結果如圖3所示。在通信半徑小于35 m的情況下，IWCLA-SAN算法的定位誤差最小，但在通信半徑大于等于35 m的情況下，ELM算法較IWCLA-SAN、BP算法和DV-Hop算法誤差小，且引入虛擬節點的ELM算法較ELM算法定位誤差平均降低了4.22 %，表明在通信半徑不同的情況下，引入虛擬節點升級次錨節點對于降低節點定位誤差有效。

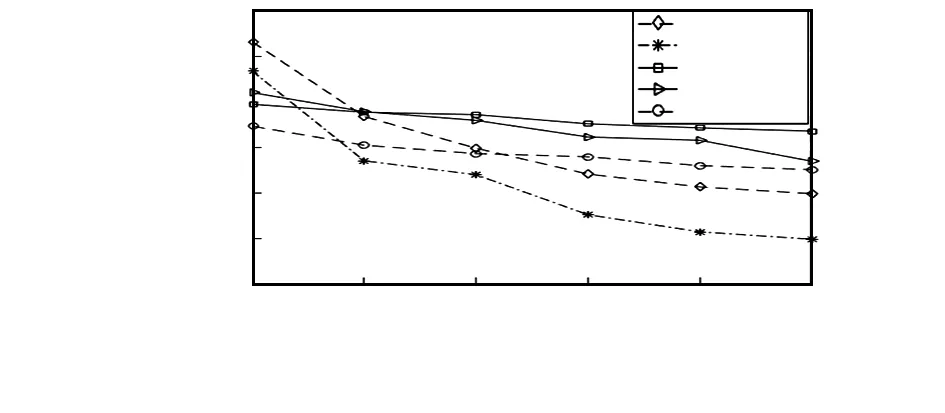
圖3 通信半徑和定位誤差的關系

3.3 總節點數對定位誤差的影響

對不同總節點數目進行仿真，仿真通信半徑為40 m，錨節點比例為10 %，仿真結果如圖4所示。當總節點數小于300個時，IWCLA-SAN算法的定位誤差最小，但當總節點數大于等于300個時，ELM算法較IWCLA-SAN算法，BP算法及DV-Hop算法誤差都要小，且引入虛擬節點的ELM算法較ELM算法定位誤差平均降低了3.56 %，亦說明在總節點數目不同的時，引入虛擬節點升級次錨節點對于降低節點定位誤差有效。

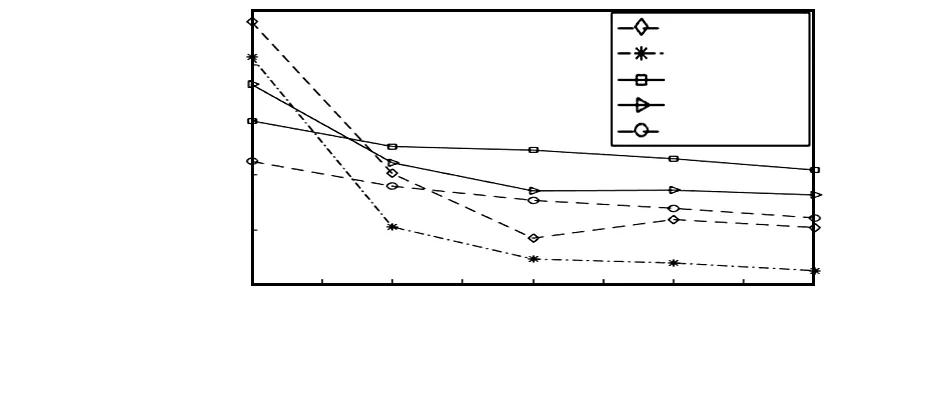
圖4 總節點數和定位誤差的關系

4 結 論

采用虛擬節點和ELM算法結合的算法選出次錨節點來提高錨節點比例，降低定位誤差。在錨節點所占比例，通信半徑，總節點數目變化的情況下，均可以減小定位誤差，說明本文算法可以有效減小定位誤差。算法總體較DV-Hop算法和BP定位算法的誤差小，適用于無線傳感器網絡的定位，但對于錨節點比例和通信半徑以及總節點數目有一定的要求。

參考文獻:

[1] 彭 宇，王 彤.無線傳感器網絡定位技術綜述[J].電子測量與儀器學報，2011,25(5):389-399.

[2] 莫宏偉，董會元，基于光電傳感器的移動機器人室內定位[J].自動化技術與應用，2014,33(10)：33-36.

[3] 楊石磊,樊曉平,劉少強,等.一種改進的無線傳感器網絡DV-Hop定位算法[J].計算機測量與控制,2008,16(9):1356-1358.

[4] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:A new learning scheme of feedforward neural networks[C]∥2004 Proceedings of IEEE International Joint Conference on Neural Networks,IEEE,2005:985-990.

[5] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine: Theory and applications[J].Neurocomputing,2006,70(1-3):489-501.

[6] 王 雷，沈龍云，孫毅剛.基于ELM的航空發動機傳感器故障診斷方法研究[J].傳感器與微系統,2015,34(4):16-18.

[7] Liu R,Sun K,Shen J.BP localization algorithm based on virtual nodes in wireless sensor networks[C]∥Proceedings of the 6th International Conference on Wireless Communications,Networking and Mobile Computing,WiCOM’10,2010:351-355.

[8] Zhao L Z,Wen X B,Li D.Amorphous localization algorithm based on BP artificial neural network[C]∥International Confe-rence on Software Intelligence Technologies and Applications & International Conference on Frontiers of Internet of Things,IET,2015.

[9] 龍 佳,卑璐璐,張 申,等.基于虛擬信標節點的改進加權質心定位修正算法[J].微電子學與計算機,2017,34(3):74-78.

[10] 衣 曉，王梓有，薛興亮.一種基于次錨節點的無線傳感器網絡質心定位算法[J].計算機應用與軟件，2013,30(6):116-120.

[11] 張先超,劉興長,張春園.基于次錨節點的無線傳感器網絡改進加權質心定位算法[J].傳感器與微系統,2015,34(2):143-146.