三角排布圓形陣列天線降維STAP研究
殷俊 張仁李 盛衛星

摘 要:????? 本文對彈載三角排布圓形陣列天線STAP處理器的降維處理方法進行了研究。 針對現有子陣劃分的不足, 提出了一種應用于彈載三角排布圓形陣列的子陣劃分方法, 該方法采取矩形框行列步進固定長度遍歷圓陣來實現子陣旋轉布陣。 仿真分析對比了這種子陣劃分方法與其他子陣劃分方法在不同旋轉角度下的雜波抑制性能。 結果表明: 本文子陣劃分方案雜波抑制性能接近最優, 不會產生角度模糊, 并且在不同旋轉角度下性能保持穩定, 可用于現實旋轉彈載圓形陣的STAP。
關鍵詞:???? 空時自適應處理; 圓形陣列; 空域降維; 相控陣雷達
中圖分類號:??? TN957.2; V243.2文獻標識碼:??? A文章編號:???? 1673-5048(2018)01-0071-06
0 引? 言
空時聯合自適應處理(STAP)技術是機載、 彈載雷達在強雜波環境中進行地面慢速運動目標檢測的一種有效方法。 該方法可以解決由雷達平臺運動導致的雜波譜展寬問題, 可有效抑制雜波, 提高雷達對淹沒在雜波中的慢速運動目標的檢測能力。 STAP技術應用于機載場景時為側視陣, 雜波的空時分布呈線性關系, 而應用于彈載場景時為前視陣, 此時, 雜波的空時分布隨距離非均勻變化, 雜波譜展寬, 雜波的空時分布呈現橢圓分布。
在相控陣雷達中相控陣天線是最為重要的內容, 通常相控陣天線有多種形式, 如線性陣列、 矩形陣列、 圓形陣列, 三角排布圓形陣列已經在彈載前視雷達中廣泛應用。 由于實際天線陣元數目龐大, 難以實現陣元級的STAP處理, 所以需要進行空域降維處理。
關于子陣級STAP問題, 文獻[1]研究了兩種非均勻子陣結構, 提出構成子陣的相鄰子陣中心間距無公約數原則。 文獻[2]基于子陣級和差波束方向圖性能提出了基于錐削函數的子陣優化方法。 文獻[3]分析了等規模交疊子陣劃分對STAP的影響。 文獻[4]提出了等噪聲功率法及等子陣加權法的子陣劃分準則, 并研究了子陣劃分對STAP的影響。 上述子陣劃分方法是基于傳感器等間隔排列的線形陣列(或矩形平面陣列), 給實際非線性陣列提供參考。 而對于圓形前視天線的子陣級STAP研究資料較少, 國內幾乎空白。 Klemm對圓形前視天線的STAP進行了研究, 提出圓形陣列的子陣劃分的三種方法: 不規則子陣、 棋盤形子陣、 圓靶形子陣。 子陣數目相同且不錐削條件下, 上述三種方法的雜波抑制性能幾乎相同, 不過沒有考慮彈載陣面旋轉對雜波抑制性能的影響[5]。
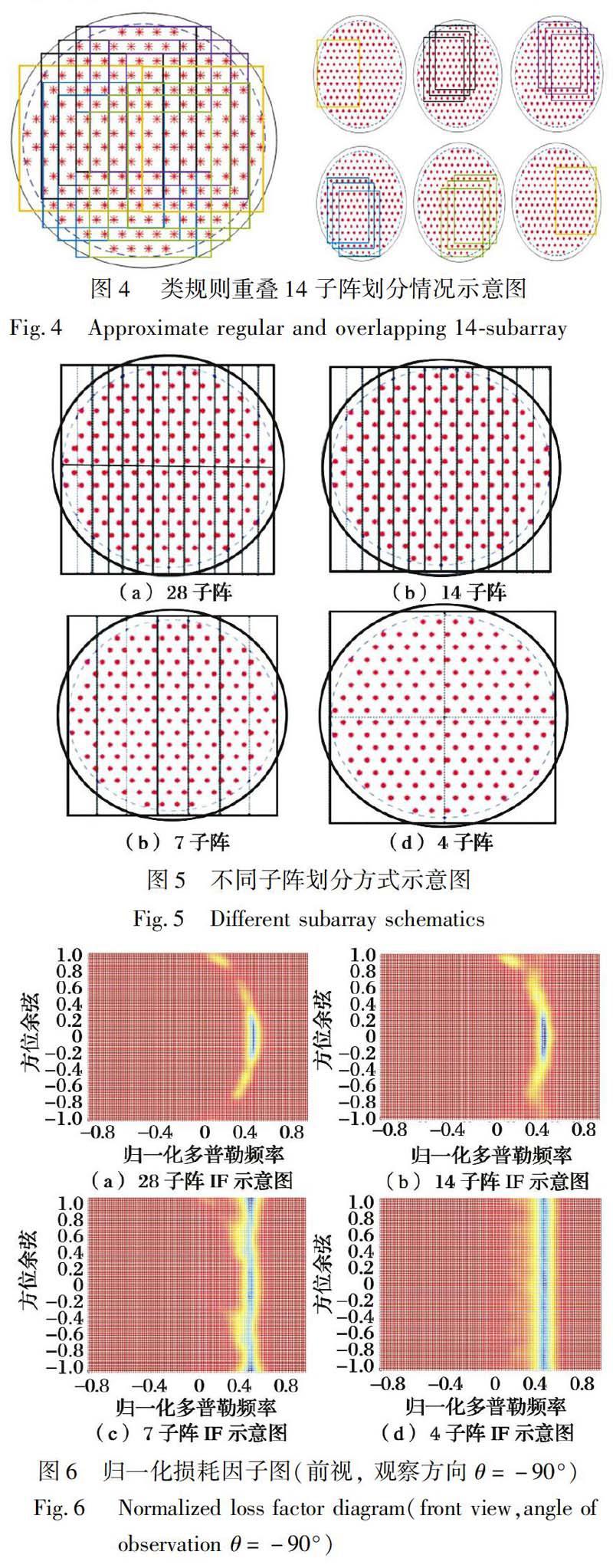
本文對基于三角排布圓形陣列彈載條件下的降維STAP處理模型進行了研究。 在棋盤形子陣的基礎上, 提出了一種基于類規則重疊子陣的新型子陣劃分方法, 給出了在這種子陣劃分情況下的空時聯合處理結構, 仿真分析對比了該子陣劃分方法與其他子陣劃分方法在不同旋轉角度下的雜波抑制性能。
平面在雜波處均形成有效零陷, 沒有產生角度模糊; 比較10(d)各旋轉角度下雜波抑制性能, 可以發現IF性能保持穩定, 彈體旋轉時有魯棒的雜波抑制性能。 與前面的子陣劃分方案相比, 在陣面旋轉時也有較好的雜波抑制能力, 可以在彈載旋轉條件下進行正常的空時處理。
4 結 束 語
本文對基于三角排布圓形陣列列彈載條件下, STAP降維處理器模型進行了研究, 并仿真對比了新型子陣劃分方法與其他子陣劃分方法在不同旋轉角度下的雜波抑制性能。 結果表明, 該子陣劃分方案雜波抑制性能接近最優, 不會產生角度模糊, 并且在不同旋轉角度下性能保持穩定, 可用于現實旋轉彈載圓形陣的STAP。 希望能夠為開展三角排布圓形相控陣導引頭陣列STAP研究提供參考。
參考文獻:
[1] Nickel U.Subarray Configurations for Interference Suppression with Array Radar [C]∥Proceedings of? International? Conference on Radar, Paris, France, 1989: 82-86.
[2] Nickel U.Subarray Configurations for Digital Beamforming with Low Sidelobes and Adaptive Interference Suppression [C]∥Proceedings of IEEE International Radar Conference, Alexandria, USA, 1995: 714-719.
[3] Gaffney J B, Guttrich G, Babu B N S, et al.Performance Comparison of Fast-Scan GMTI /STAP Architectures [C]∥Proceedings of IEEE International Radar Conference, 2001: 252-257.
[4] Xu Z Y, Bao Z, Liao G S.A Method of Designing Irregular Subarray Architectures for Partially Adaptive Processing[C]∥Proceedings of CIE International Conference on Radar, 2002: 461-464.
[5] Klemm R.STAP for Circular Forward Looking Array Antennas [C]∥Proceedings of Radar 97, 1997: 14-16.
[6] 王永良, 彭應寧.空時自適應信號處理 [M].北京: 清華大學出版社, 2000: 58-103.
Wang Yongliang, Peng Yingning.Spatial-Temporal Adaptive Singal Processing [M].Beijing: Tsinghua University Press, 2000: 58-103.(in Chinese)
[7] Klemm R.空時自適應處理原理 [M]. 3版. 北京: 高等教育出版社, 2009: 98.
Klemm R.Principles of Space-Time Adaptive Processing [M].3rd ed. Beijing: Higher Education Press, 2009: 98.(in Chinese)
[8] 袁漢欽, 陳璽羽.三角形柵格圓口徑平面相控陣天線的分析與計算 [J].四川兵工學報, 2014, 35(11): 31-33.
Yuan Hanqin, Chen Xiyu.Calculations and Analysis of the Triangle-Grid Taylor and Bayliss Circular-Aperture Phased Array Antenna [J].Journal of Sichuan Ordnance, 2014, 35(11) : 31-33.(in Chinese)
[9] 伍勇, 湯俊, 彭應寧.雷達系統雜波自由度研究 [J].電子與信息學報, 2008, 30(5): 1032-1036.
Wu Yong, Tang Jun, Peng Yingning.On Clutter Degrees of Freedom of the Radar System[J]. Journal of Electronics & Information Technology, 2008, 30(5): 1032-1036.(in Chinese)
[10] 陳曦, 傅光, 龔書喜, 等.陣列天線相位中心的測量方法研究 [J].微波學報,? 2011, 27(1): 36-39.
Chen Xi, Fu Guang, Gong Shuxi, et al.Study on Mea-surement of Phase Center of Array Antenna[J]. Journal of Microwaves, 2011, 27(1):? 36-39.(in Chinese)

