基于壓縮感知的擴(kuò)頻信號統(tǒng)一捕獲技術(shù)
王 凱,吳 斌,汪 勃
(北京跟蹤與通信技術(shù)研究所,北京100094)
0 引言
為了應(yīng)對航天測控領(lǐng)域不同的任務(wù)模式和應(yīng)用場景,新的測控體制不斷涌現(xiàn)[1],由此對設(shè)備通用性、標(biāo)準(zhǔn)化和小型化要求越來越高。
擴(kuò)頻測控體制是我國當(dāng)前主流的測控體制,直擴(kuò)和跳頻是其中常見的2種信號體制,它們之間存在一定的差異,采用現(xiàn)有的接收設(shè)備會存在一些問題。若采用獨立接收設(shè)備,則平臺搭載的設(shè)備載荷負(fù)擔(dān)較重,可擴(kuò)展性差,不利于航天領(lǐng)域的應(yīng)用[2];如采用軟件重載接收設(shè)備,則信號體制每次改變,就需要重新加載軟件,地面到星上的延時使得系統(tǒng)的實時性受到限制[3]。因此需研究統(tǒng)一接收體制,在接收信號的過程中對不同體制的信號只需調(diào)整參數(shù),具有實時性好、通用性強的特點。
此外,測控體制存在信息保密性不足的隱患[4],新提出的提高測控頻段、擴(kuò)頻碼速率等抗干擾方法都會不同程度地增大系統(tǒng)帶寬,接收設(shè)備的采樣成本、設(shè)計難度都會急劇增加。因此有必要研究一種能夠有效降低信號采樣速率、解決其高數(shù)據(jù)率的信號處理方法。
壓縮感知[5](Compressed Sensing,CS)是新提出的一種信號采集與處理理論,它以信號稀疏表示為基礎(chǔ),提出了采樣率由信號所包含的信息量決定,而不再受限于信號帶寬[6],這為緩解采樣壓力提供了全新的途徑。并且基于壓縮感知理論的信號處理方法能用不同的稀疏矩陣和觀測矩陣對不同體制的信號進(jìn)行表達(dá),為實現(xiàn)信號統(tǒng)一接收提供了可能。
本文利用壓縮感知原理的內(nèi)在聯(lián)系,構(gòu)建了基于壓縮感知的直擴(kuò)、跳頻統(tǒng)一捕獲接收框架,實現(xiàn)過程運用復(fù)用、優(yōu)化的設(shè)計思路,節(jié)省了邏輯資源,降低了算法復(fù)雜度。仿真分析表明,提出的方法能有效捕獲直擴(kuò)、跳頻信號,成功率高、模式切換速度快,相較于軟件重載的捕獲方法,在實時性上具有更好的性能。
1 壓縮感知基本原理
壓縮感知以稀疏表示理論為基礎(chǔ),通過對信號進(jìn)行隨機投影實現(xiàn)壓縮采樣,然后由采樣值通過求解一個優(yōu)化問題重構(gòu)出原信號。其數(shù)學(xué)描述如下[7]:
設(shè)信號x∈RN在稀疏基Ψ下是K稀疏的,即
(1)
系數(shù)向量v中僅K個非零值,則可通過測量矩陣Φ投影完成壓縮采樣,獲得低維測量值y:
y=Φx=ΦΨv=Θv,
(2)
式中,Φ∈RM×N為測量矩陣;Θ=ΦΨ為感知矩陣。然后可以通過優(yōu)化算法由y恢復(fù)原信號x。由于感知矩陣Θ的行數(shù)M比列數(shù)N少,故式(1)是欠定方程,通常可以通過求解最小化l0范數(shù)問題來重構(gòu)原信號[8]。
min‖v‖l0s.t.y=Θv。
(3)
當(dāng)感知矩陣Θ滿足約束等距特性時[9],可以將式(3)等價地轉(zhuǎn)換為式(4)所示的最小化l1范數(shù)問題。
min‖v‖l1s.t.y=Θv。
(4)
2 直擴(kuò)信號CSPMF-FFT捕獲算法
PMF-FFT捕獲算法由于具備良好的性能而被廣泛應(yīng)用[10],本文在PMF-FFT捕獲算法的基礎(chǔ)上,引入壓縮感知思想,提出了CSPMF-FFT(Compressed Sensing PMF-FFT)捕獲算法。
2.1 矩陣運算模型
為了便于引入壓縮感知思想,首先建立PMF-FFT捕獲算法的矩陣運算模型。根據(jù)PMF-FFT方法基本原理[11],其捕獲過程主要包括匹配濾波和傅里葉變換2個步驟。假設(shè)匹配濾波器個數(shù)為M,每個匹配濾波器對連續(xù)的X個碼元進(jìn)行相關(guān),從而濾波器系數(shù)矩陣可表示為:
式中,ci為濾波器的抽頭系數(shù)。每一次相關(guān)時刻,數(shù)據(jù)長度為N的信號不斷滑入濾波器中,各次輸入的信號可表示為X(假設(shè)L=N):
Xi表示輸入信號矩陣中第i列向量,即為每次滑動送入匹配濾波器的信號。完成匹配濾波后,將輸出的M個相關(guān)結(jié)果做快速傅氏變換。M階的離散傅氏變換基為PFFT,其中WM=e-j2π/M。
2.2 引入壓縮感知思想
根據(jù)矩陣模型,可知完成一次PMF-FFT算法的運算過程可表示為θi=PFFTCPMFXi,將各次輸出θi重新排列組成輸出矩陣θ。由直擴(kuò)信號的強自相關(guān)性可知,當(dāng)捕獲成功時,輸出矩陣中會產(chǎn)生一個顯著的峰值,而未完成捕獲時輸出值較小,由此可知信號經(jīng)過變換在矩陣θ中呈現(xiàn)稀疏性。
根據(jù)上述分析,可以得到稀疏變換矩陣為:
Ψ=PFFTCPMF。
(5)
信號在此稀疏矩陣下的稀疏表示為:
θ=Ψx=PFFTCPMFx。
(6)
在稀疏表示后可利用測量矩陣完成壓縮測量。隨機高斯矩陣作為普適性的測量矩陣與稀疏矩陣具有良好的非相干性[12],能有效地對信號進(jìn)行壓縮觀測,得到信號的測量值:
y0=Φθ=ΦΨx,
(7)
式中,ΦM1×M為隨機高斯矩陣。獲得壓縮測量值后,通過正交匹配追蹤(OMP)算法對信號進(jìn)行重構(gòu)[13],恢復(fù)稀疏系數(shù)矩陣θ,根據(jù)θ中峰值的位置索引可以估計得到碼相位和多普勒頻偏。
CSPMF-FFT算法在每一個碼相位下進(jìn)行搜索,捕獲成功時輸出信號矩陣中存在峰值且超過門限,記錄相應(yīng)的偽碼相位并根據(jù)譜峰位置估計多普勒頻移。當(dāng)且僅當(dāng)序列碼相位完全對齊和頻率完全補償時,輸出幅值最大。算法的捕獲流程如圖1所示。
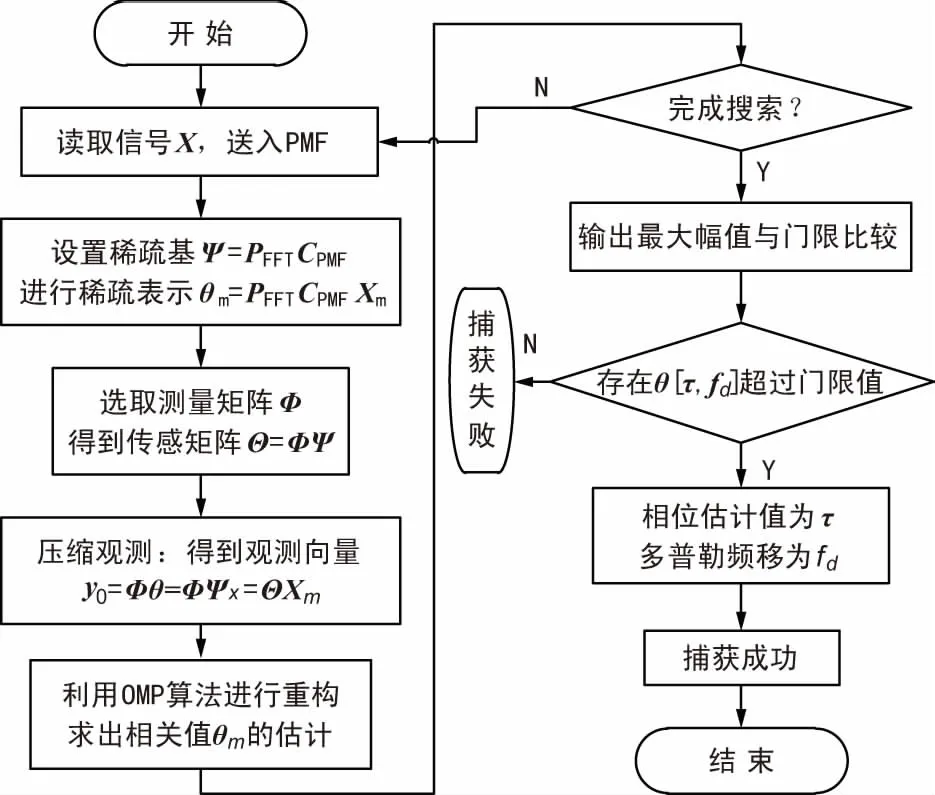
圖1 CSPMF-FFT捕獲算法流程
3 跳頻BDSA捕獲算法
基于壓縮域信號處理理論[14],提出基于塊對角稀疏分析(Block Diagonal Sparse Analysis,BDSA)的跳頻信號捕獲算法。
3.1 塊對角稀疏分析
跳頻信號在時頻域具有顯著的稀疏性,故其頻譜在頻率跳變處產(chǎn)生較大峰值[15]。但是信號在每一個時間段內(nèi)只存在一個頻率,直接采用傅里葉基只反映了其頻域特性,而沒有反映時域特性,即使能提取各頻點的頻率,也無法得到頻點跳變順序。故在捕獲時需構(gòu)造一個能同時反映其時、頻域結(jié)構(gòu)特點的稀疏矩陣。研究表明塊對角稀疏矩陣能很好地表達(dá)跳頻信號的時、頻域特性,其結(jié)構(gòu)如圖2所示[16]。

圖2 塊對角矩陣結(jié)構(gòu)
以僅包含2個頻點的信號為例進(jìn)行分析,依據(jù)可能出現(xiàn)的跳頻頻率和跳變時刻構(gòu)建2個子對角塊,即對k=1,2,...,N-1,構(gòu)造k×k維傅里葉正交矩陣Ψk,1和(N-k)×(N-k)維傅里葉正交矩陣Ψk,2,并將矩陣Ψk,1和Ψk,2作為對角塊構(gòu)造稀疏矩陣Ψk:
構(gòu)造Ψk時其子塊矩陣維數(shù)有3種情況,如圖3所示。無論是k
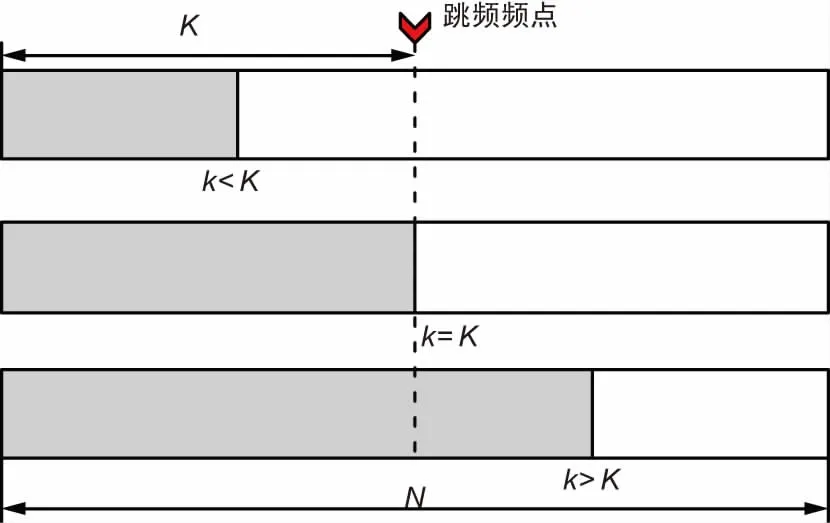
圖3 塊對角矩陣維數(shù)情況
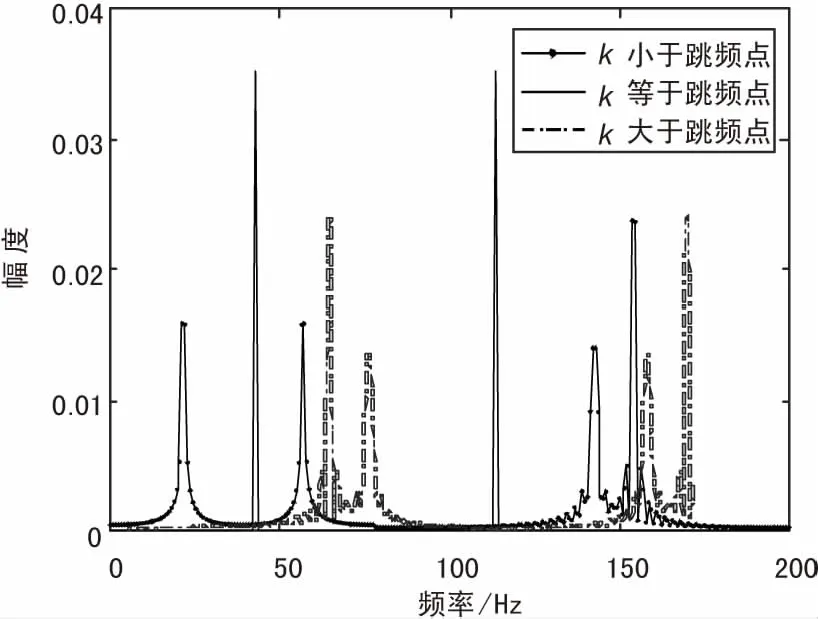
圖4 不同矩陣情況下信號稀疏變換
3.2 引入壓縮感知思想
首先用M×N維的高斯隨機矩陣Φ對信號X進(jìn)行壓縮測量,獲取測量值Y:
Y=ΦX=ΦΨkak=Θkak。
(8)
信號X在塊對角稀疏矩陣Ψk下被表達(dá)為:
X=a1(K)×ΨK,P1(K)+a2(K)×ΨK,P2(K),
(9)
式中,a1(K)和a2(K)為稀疏系數(shù)向量ak中存在的2個顯著的非零系數(shù);P1(k)和P2(k)為a1(K)和a2(K)在向量ak中的位置P2(k)。則壓縮采樣值Y可表示為:
Y=Θkak=a1(K)×θK,P1(K)+a2(K)×θK,P2(K)。
(10)
壓縮測量值Y與感知矩陣Θk中的每一個列向量θk,i(i=1,2,3,...,N)進(jìn)行相關(guān)運算,相應(yīng)的表達(dá)式為:
(11)
當(dāng)k≠K時,信號X在矩陣Ψk上不能完全稀疏表達(dá),故得到的a1(K)和a2(K)相比k=K時小很多。因此可通過求解γ=α1(k)2+α2(k)2(k=1,2,3,...,N-1)的最大值估計參數(shù)K。
根據(jù)得到的跳變時刻K,通過P1(k)和P2(k)可以估計出信號中包含的2個頻點頻率f1和f2:
f1=(P1(k)-1)×fs/K,
(12)
f2=(P2(k)-K-1)×fs/(N-K),
(13)
式中,fs=1/Ts為奈奎斯特采樣率;N為一跳信號的采樣點數(shù)。總結(jié)基于壓縮感知的BDSA跳頻信號參數(shù)估計算法的流程圖如圖5所示。
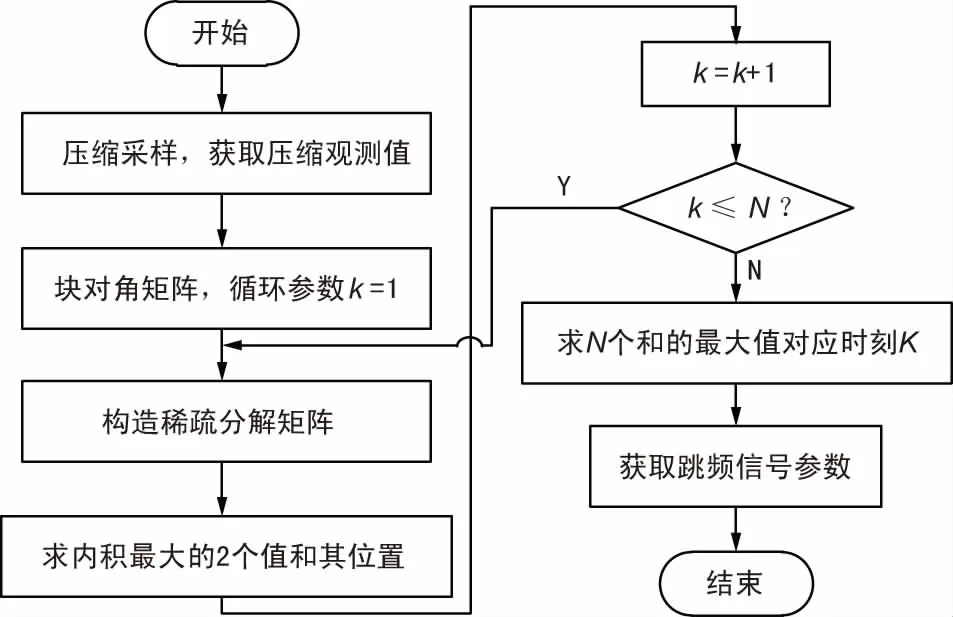
圖5 BDSA捕獲算法流程
4 統(tǒng)一捕獲接收框架
基于壓縮感知的擴(kuò)頻信號處理,能用不同的稀疏矩陣作為參數(shù)對不同體制信號稀疏表示,并輔以不同的測量矩陣進(jìn)行壓縮測量,最后通過重構(gòu)算法或壓縮域信號處理實現(xiàn)捕獲。通過壓縮感知理論的內(nèi)在聯(lián)系,搭建擴(kuò)頻信號統(tǒng)一接收框架,通過對不同體制信號的公共模塊的提取,利用不同的參數(shù)實現(xiàn)同一模塊的共用,完成對直擴(kuò)和跳頻2種體制信號的統(tǒng)一接收,統(tǒng)一接收框架如圖6所示。
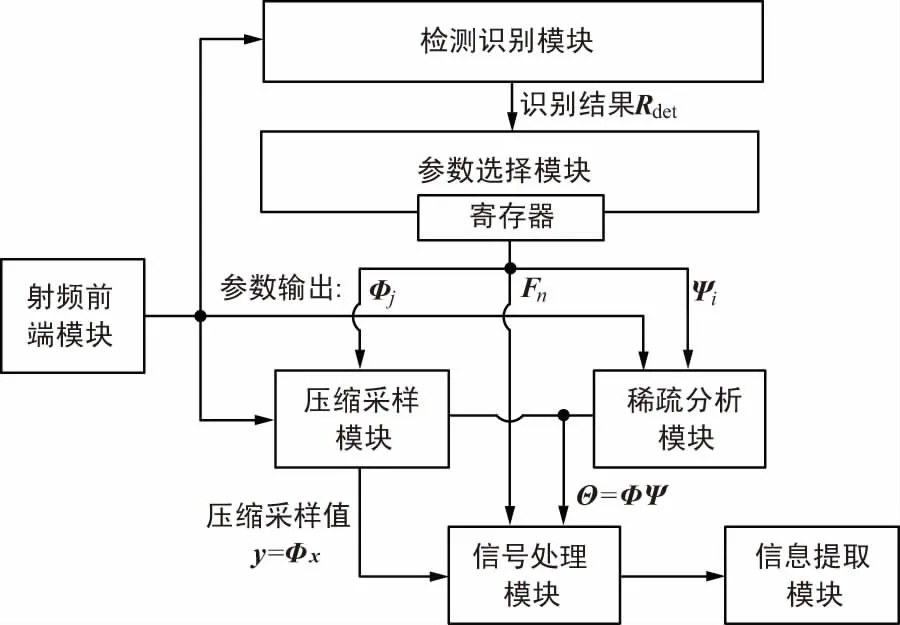
圖6 基于壓縮感知原理的擴(kuò)頻統(tǒng)一接收框架
由圖6可知,擴(kuò)頻信號統(tǒng)一捕獲框架主要包括:射頻前端模塊、檢測識別模塊、參數(shù)選擇模塊、壓縮采樣模塊、稀疏分析模塊、信號處理模塊和信息提取模塊。
在各模塊中,壓縮采樣模塊、稀疏分析模塊和信號處理模塊是基于壓縮感知的統(tǒng)一捕獲框架的核心組成部分。射頻前端模塊和信息提取模塊是系統(tǒng)的前后端信號處理部分,為整系統(tǒng)的運行提供保障。檢測識別模塊和參數(shù)選擇模塊是多體制信號統(tǒng)一處理模塊的必要組成部分,為整系統(tǒng)的順利運行提供支撐。
確定統(tǒng)一接收系統(tǒng)中的各項參數(shù),如表1所示。
表1擴(kuò)頻信號統(tǒng)一接收框架參數(shù)
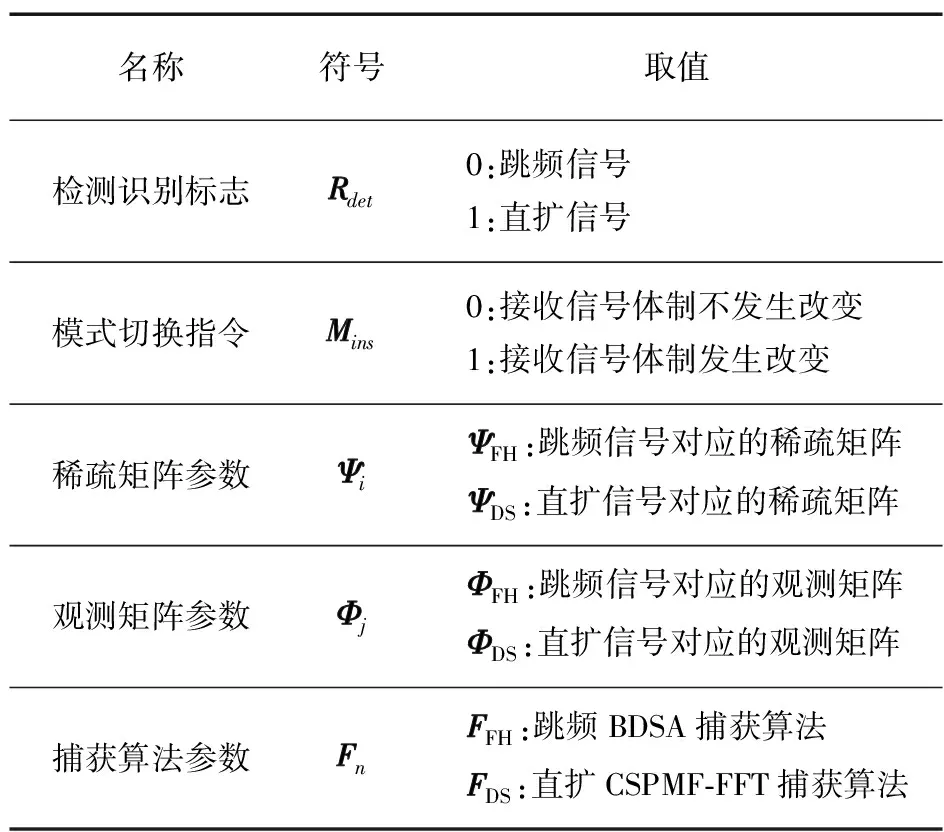
名稱符號取值檢測識別標(biāo)志Rdet 0:跳頻信號 1:直擴(kuò)信號模式切換指令Mins 0:接收信號體制不發(fā)生改變 1:接收信號體制發(fā)生改變稀疏矩陣參數(shù)Ψi ΨFH:跳頻信號對應(yīng)的稀疏矩陣 ΨDS:直擴(kuò)信號對應(yīng)的稀疏矩陣觀測矩陣參數(shù)Φj ΦFH:跳頻信號對應(yīng)的觀測矩陣 ΦDS:直擴(kuò)信號對應(yīng)的觀測矩陣捕獲算法參數(shù)Fn FFH:跳頻BDSA捕獲算法 FDS:直擴(kuò)CSPMF?FFT捕獲算法
基于統(tǒng)一捕獲框架,設(shè)計統(tǒng)一捕獲算法流程如下:
① 前端天線接收信號x,經(jīng)前端模塊處理后的信號被分別送入檢測識別模塊、壓縮采樣模塊和稀疏分析模塊。
② 檢測識別模塊調(diào)用檢測識別算法,判斷接收信號為跳頻體制還是直擴(kuò)體制,通過判決結(jié)果給Rdet賦值0或者1,并送入?yún)?shù)選擇模塊;模式切換指令Mins預(yù)置0表示接收體制不發(fā)生改變,當(dāng)接收體制發(fā)生改變時設(shè)置為1。
③ 參數(shù)選擇模塊接收到檢測識別符Rdet后,從寄存器中選擇相應(yīng)的稀疏矩陣Ψi送入稀疏分析模塊,觀測矩陣Φj送入壓縮采樣模塊,捕獲算法Fn送入信號處理模塊。
④ 稀疏分析模塊和壓縮采樣模塊在接收到參數(shù)后啟動工作,稀疏分析模塊對信號進(jìn)行稀疏分析提供理論先驗:x=Ψv;壓縮采樣模塊完成對接收信號x的壓縮測量:y=Φx;完成后將壓縮采樣值y和感知矩陣Θ=ΦΨ送入信號處理模塊。
⑤ 信號處理模塊調(diào)用捕獲算法Fn進(jìn)行捕獲處理,完成捕獲并輸出捕獲信息,經(jīng)信息提取模塊處理后輸出測距、測速等信息。
⑥ 當(dāng)接到模式切換指令Mins時,重復(fù)步驟①~⑤;當(dāng)不再有數(shù)據(jù)輸入時,停止工作。通過模式切換指令的調(diào)度,當(dāng)信號體制不發(fā)生改變時可以節(jié)省參數(shù)加載時間。
5 仿真分析與實驗
5.1 CSPMF-FFT直擴(kuò)捕獲算法仿真分析
對提出的CSPMF-FFT算法進(jìn)行仿真驗證。考慮BPSK調(diào)制的擴(kuò)頻信號,載頻4 MHz,碼長1 023,信息速率1 kB/s,碼速率Rc=10.23 Mc/s,碼周期1/Rc,每個碼元采集2個點,即采樣率fs=2Rc,相關(guān)處理時間為1 ms。仿真中頻偏設(shè)為8 500 Hz,偽碼相位延遲為275,匹配濾波器個數(shù)M=64,每個濾波器相關(guān)積分碼元數(shù)X=16,輸出做256點FFT運算。
在壓縮比為2的情況下,采用CSPMF-FFT算法對信號進(jìn)行捕獲,重構(gòu)恢復(fù)得到離散輸出譜峰如圖7所示,對離散普峰值做曲線擬合,估得多普勒頻偏為8 750 Hz,此時多普勒頻偏分辨率Δfd=1/(MXTc)為250 Hz。匹配濾波相關(guān)輸出幅值如圖8所示,在碼元相位為275成功捕獲時產(chǎn)生一個顯著的峰值。可見CSPMF-FFT算法能有效地捕獲直擴(kuò)信號并估計出信號的相位信息和多普勒頻偏。
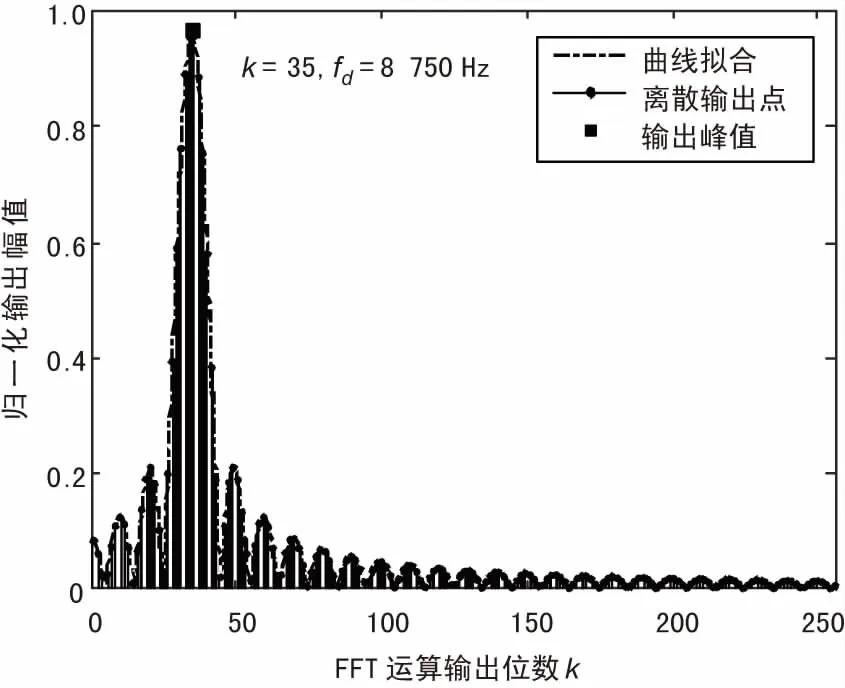
圖7 離散重構(gòu)譜峰與FFT變換位數(shù)關(guān)系
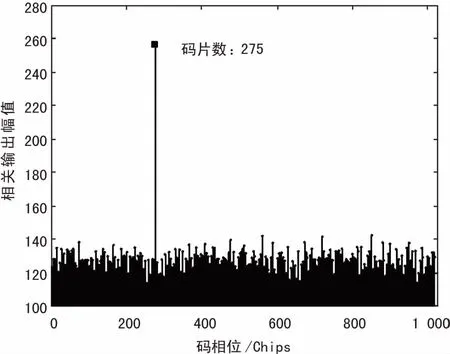
圖8 相關(guān)輸出幅度隨碼相位變換關(guān)系
在不同的信噪比和壓縮比情況下,對CSPMF-FFT方法的捕獲概率進(jìn)行仿真,結(jié)果如圖9所示。可見捕獲概率隨著信噪比的提高而上升,隨著壓縮比的提高而下降。在壓縮比等于2的情況下,當(dāng)信噪比大于-10 dB時捕獲成功率達(dá)到90%以上,可認(rèn)為CSPMF-FFT算法能有效地捕獲直擴(kuò)信號。
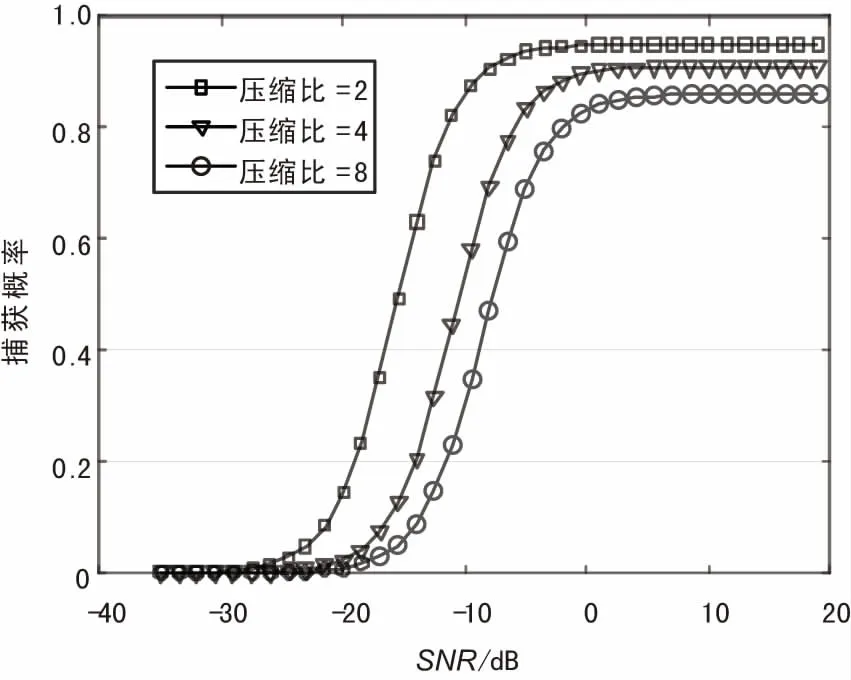
圖9 直擴(kuò)信號捕獲概率
5.2 BDSA跳頻捕獲算法仿真分析
對BDSA跳頻信號捕獲算法的性能進(jìn)行仿真分析,本質(zhì)上是分析捕獲算法對跳頻頻點和跳變時刻這2個參數(shù)的估計性能。設(shè)置跳頻信號的仿真參數(shù)為:跳頻點為{1.0,1.1,1.2,1.3,1.4,1.5,1.6,1.7} kHz,載波頻率隨機變化;跳頻周期為200 ms,采樣頻率fc=4 kHz。在不同的信號信噪比下,考慮不同的壓縮比,對參數(shù)進(jìn)行估計,跳變時刻的估計成功率與跳變時刻的捕獲成功率如圖10和圖11所示。
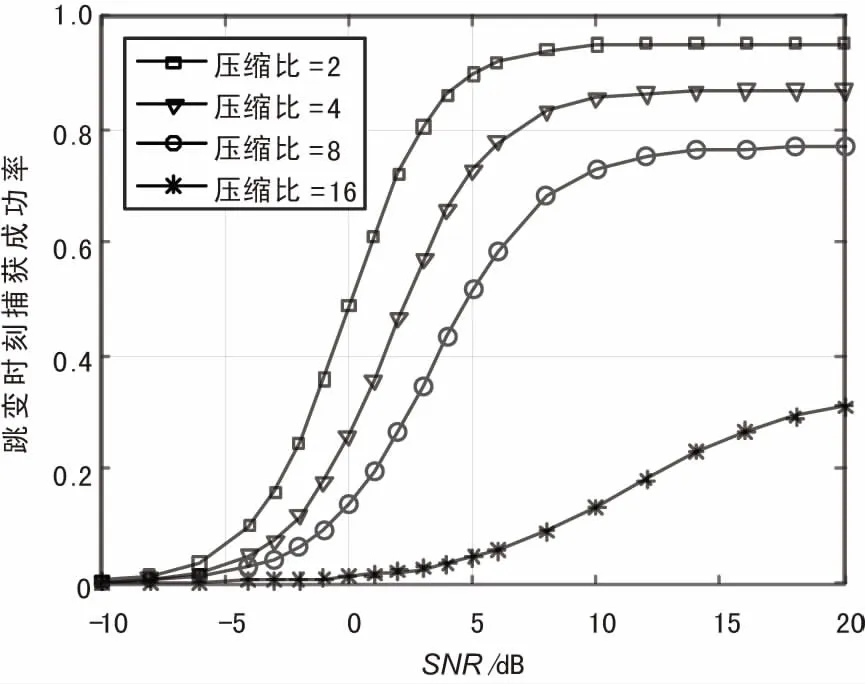
圖10 跳變時刻捕獲成功率
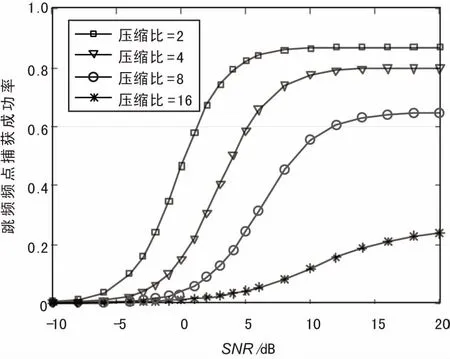
圖11 跳頻頻點捕獲成功率
圖10和圖11的仿真結(jié)果顯示,對跳變時刻和跳頻頻點的捕獲概率隨信噪比的提高而上升,而當(dāng)信噪比增大到一定程度時,捕獲成功率維持在一個穩(wěn)定值而不再繼續(xù)上升。在信噪比相同的情況下,捕獲概率隨著壓縮比的增大而下降。在壓縮比為2、信噪比大于5 dB時,對跳變時刻的捕獲成功率達(dá)到90%以上,對跳頻頻點的捕獲成功率達(dá)到80%以上,此時能對跳變時刻和跳頻頻點有效地進(jìn)行估計。當(dāng)壓縮比達(dá)到16時,捕獲算法失效。相較于對跳變時刻的估計,在相同的信噪比與壓縮比條件下對跳頻頻點估計概率較低,這是由于對頻點的估計是建立在跳變時刻正確估計的基礎(chǔ)之上,相應(yīng)的捕獲性能也因此有所下降。
5.3 統(tǒng)一捕獲框架仿真分析
對擴(kuò)頻信號統(tǒng)一捕獲接收框架進(jìn)行仿真驗證,系統(tǒng)的有效性和實時性是衡量其工作狀況的2個重要指標(biāo),前面已經(jīng)對捕獲算法的有效性進(jìn)行了分析,故此處主要針對實時性展開分析。
統(tǒng)一捕獲系統(tǒng)實時性主要體現(xiàn)為不同體制模式切換時的實時性和對信號進(jìn)行捕獲的實時性。設(shè)定模式切換下直擴(kuò)信號捕獲工作模式和跳頻信號捕獲工作模式,分別記錄下二者模式切換加信號捕獲的總時間,與軟件重載模式下對2種信號捕獲的時間進(jìn)行對比。
① 直擴(kuò)信號實時性驗證示意圖如圖12所示。直擴(kuò)信號捕獲工作模式,記錄模式切換開始工作的時刻tDS1,生成直擴(kuò)信號并對其進(jìn)行捕獲,記錄捕獲完成的時間tDS2,則工作模式切換加上直擴(kuò)捕獲的總時間為:
ΔtDS=tDS2-tDS1。
(14)
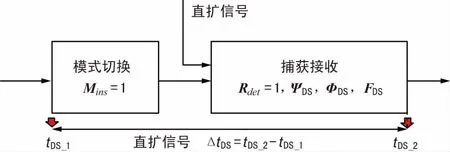
圖12 直擴(kuò)信號實時性驗證示意
② 跳頻信號實時性驗證示意圖如圖13所示。跳頻信號捕獲工作模式,記錄模式切換開始工作的時刻tFH1,生成跳頻信號并對其進(jìn)行捕獲,記錄捕獲完成的時間tFH2,則工作模式切換和跳頻信號捕獲的總時間為:
ΔtFH=tFH2-tFH1。
(15)
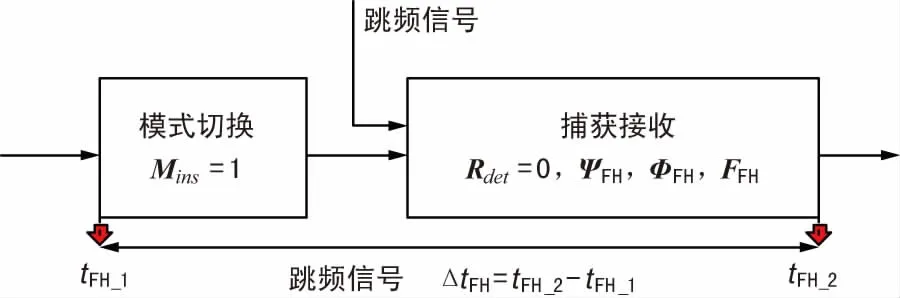
圖13 跳頻信號實時性驗證示意
③ 軟件重載信號捕獲仿真驗證示意圖如圖14所示。軟件重載信號捕獲工作模式,作為對比,加入基于軟件重載的捕獲接收過程,此處僅考慮仿真軟件重載程序,并未考慮設(shè)備間程序加注所需的信息傳輸、設(shè)備啟閉等其他時間。記錄完成上一次捕獲的時間tall1,然后通過仿真軟件重載程序,首先生成直擴(kuò)信號并對其進(jìn)行捕獲,然后再重載一次程序,生成跳頻信號并對其進(jìn)行捕獲,記錄捕獲完成的時間tall2,則該工作模式完成軟件重載和2種信號捕獲的總時間為:
Δtall=tall2-tall1。
(16)
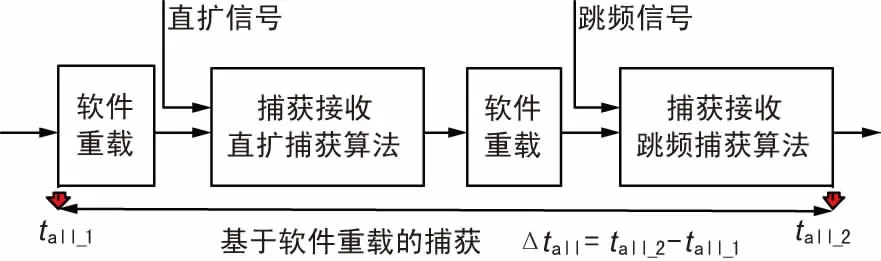
圖14 軟件重載信號捕獲仿真驗證示意
將模式切換捕獲時長ΔtDS和ΔtFH作為捕獲框架實時性的驗證指標(biāo),Δtall作為對照,利用仿真軟件獨立重復(fù)進(jìn)行10次實驗,由于耗時較小,因此每次實驗重復(fù)進(jìn)行5次模式切換及捕獲過程,測取時長的平均值以克服隨機性帶來的偏差,對比結(jié)果如表2所示。
表2統(tǒng)一捕獲與軟件重載捕獲耗時對比結(jié)果
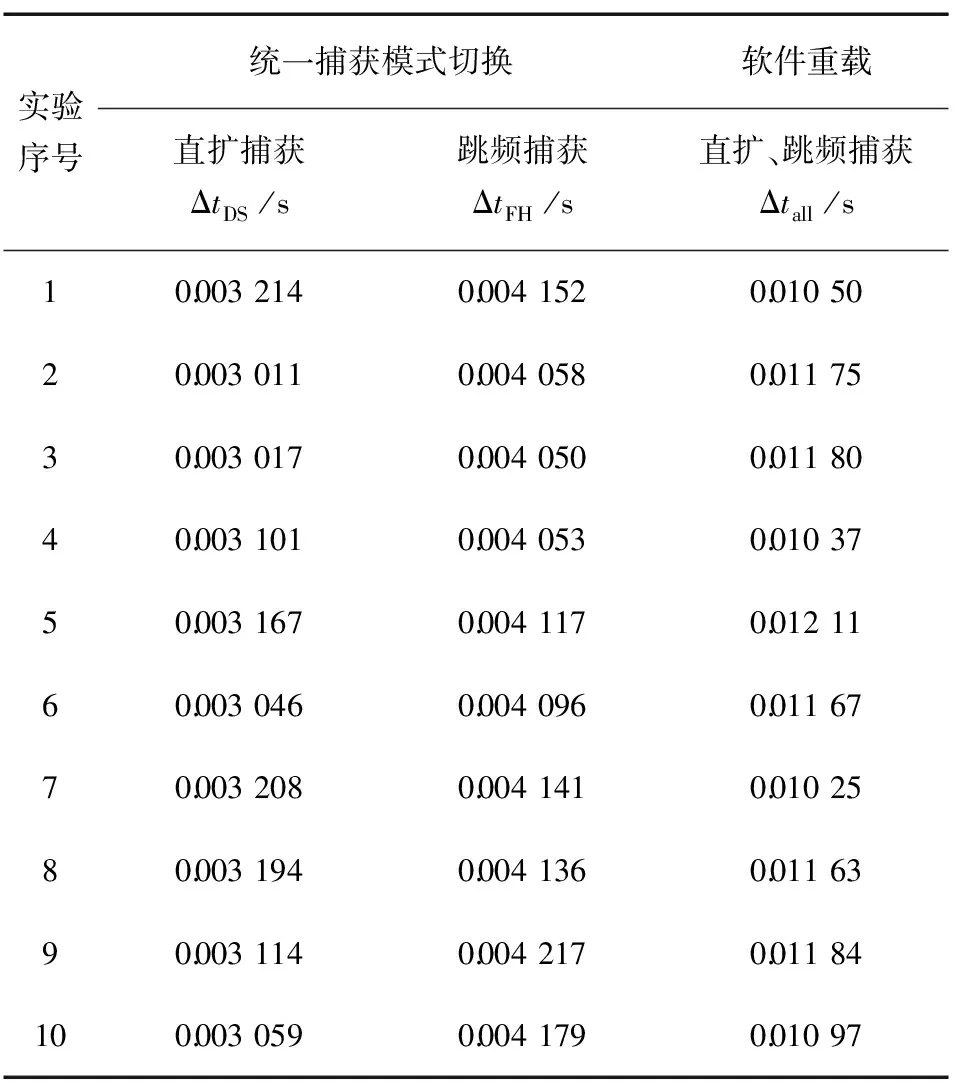
實驗序號統(tǒng)一捕獲模式切換軟件重載直擴(kuò)捕獲ΔtDS/s跳頻捕獲ΔtFH/s直擴(kuò)、跳頻捕獲Δtall/s10.0032140.0041520.0105020.0030110.0040580.0117530.0030170.0040500.0118040.0031010.0040530.0103750.0031670.0041170.0121160.0030460.0040960.0116770.0032080.0041410.0102580.0031940.0041360.0116390.0031140.0042170.01184100.0030590.0041790.01097
仿真實驗結(jié)果表明,捕獲系統(tǒng)對2種體制的信號能以小于0.005 s的時間完成模式切換及信號捕獲,從而驗證了捕獲框架的實時性。并且相較于軟件重載的捕獲方法,完成2種信號捕獲的時間總和小于軟件重載完成2種信號捕獲的時間,并且這是在未考慮設(shè)備間程序加注所需的信息傳輸、設(shè)備啟閉等其他時間的情況下完成的,可見提出的統(tǒng)一捕獲框架在實時性上具有更加優(yōu)異的性能。
6 結(jié)束語
針對當(dāng)前航天測控領(lǐng)域多體制信號捕獲時接收設(shè)備存在的設(shè)備載荷負(fù)擔(dān)重、采樣壓力大和實時性受限等問題,本文在對直擴(kuò)、跳頻壓縮感知捕獲算法分別進(jìn)行研究的基礎(chǔ)上,提取了信號稀疏分析、壓縮觀測和信號捕獲的共用模塊并進(jìn)行了合理的復(fù)用與優(yōu)化,構(gòu)建了基于壓縮感知原理的擴(kuò)頻統(tǒng)一捕獲框架。仿真結(jié)果表明,提出統(tǒng)一接收框架能有效地對擴(kuò)頻信號進(jìn)行捕獲接收,在對信號捕獲實時性上相較于軟件重載的捕獲方法具有更好的性能。全文通過對以上內(nèi)容的研究,將新穎的壓縮感知思想引入到擴(kuò)頻信號捕獲接收技術(shù)研究中,不僅為解決當(dāng)前擴(kuò)頻測控通信系統(tǒng)面臨的問題提供了思路,也將為其未來的發(fā)展帶來啟發(fā)。研究成果能為測控設(shè)備小型化和信號處理任務(wù)的時效性帶來幫助,對于資源受限、分秒必爭的航天領(lǐng)域,將產(chǎn)生重大的影響。
[1]劉嘉興.飛行器測控與信息傳輸技術(shù)[M].北京:國防工業(yè)出版社,2015:13-20.
[2]王遠(yuǎn),姚艷軍,王爍.我國天基信息網(wǎng)未來發(fā)展設(shè)想[J].信息通信,2014(1):91-92.
[3]李志剛,張彧,潘長勇,等.抗單粒子翻轉(zhuǎn)的可重構(gòu)衛(wèi)星通信系統(tǒng)[J].宇航學(xué)報,2009,30(5):1752-1756.
[4]黃慈寧.測控通信非常規(guī)抗跟蹤干擾方法研究[D].西安:西安電子科技大學(xué),2015.
[5]DONOHO D L.Compressed Sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[6]HAYASHI K,NAGAHARA M,TANAKA T.A User’s Guide to Compressed Sensing for Communications Systems[J].Ieice Transactions on Communications,2013,E96-B(3):685-712.
[7]BOUGHER B.Introduction to Compressed Sensing[J].Leading Edge,2015,34(10):1256-1257.
[8]CANDES E J,ROMBERG J,TAO T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].Information Theory IEEE Transactions on,2006,52(2):489-509.
[9]BARANIUK R,DAVENPORT M,DEVORE R,et al.A Simple Proof of the Restricted Isometry Property for Random Matrices[J].Constructive Approximation,2008,28(3):253-263.
[10] 楊秦彪,王祖林,黃勤,等.高動態(tài)鏈路中折疊PMF-FFT快速捕獲方法[J].系統(tǒng)工程與電子技術(shù),2016,38(8):1723-1729.
[11] QI J,LUO F,SONG Q.Fast Acquisition Method of Navigation Receiver Based on Folded PMF-FFT[C]∥Computing,Communications and It Applications Conference,IEEE,2015:62-66.
[12] 王俠,王開,王青云,等.壓縮感知中的確定性隨機觀測矩陣構(gòu)造[J].信號處理,2014,30(4):436-442.
[13] JIAN W,KWON S,SHIM B.Generalized Orthogonal Matching Pursuit[J].IEEE Transactions on Signal Processing,2011,60(12):6202-6216.
[14] 程艷合,楊文革,屈文星,等.壓縮域直擴(kuò)測控通信信號載波同步技術(shù)[J].電訊技術(shù),2015,55(6):585-593.
[15] 張益東,楊文革.基于壓縮感知的跳頻信號接收處理方法綜述[J].通信技術(shù),2016,49(4):383-390.
[16] 邱硯馳.基于壓縮感知的跳頻信號盲處理系統(tǒng)的設(shè)計與實現(xiàn)[D].西安:西安電子科技大學(xué),2015.
[17] 張春磊,李立春,王大鳴.壓縮域?qū)拵l信號跳變時刻估計算法[J].太赫茲科學(xué)與電子信息學(xué)報,2015,13(1):122-129.

