基于BWRS狀態方程的天然氣偏差因子計算方法
張立俠 郭春秋
中國石油勘探開發研究院
天然氣偏差因子(Z)通常又稱壓縮因子或偏差系數,它表征了某一壓力、溫度條件下相同數量真實氣體和理想氣體的體積之比,是油氣藏工程計算常用的重要參數;為避免與氣體壓縮系數(Cg)混淆,后文均稱之為偏差因子。確定偏差因子的方法主要有實驗測量、圖版法和計算法3類。實驗法雖然直接可靠,但耗時、成本高,而圖版法或查表則不能得到連續的值,因此,計算法以其簡便性和實用性得到了廣泛應用。計算法主要是利用能夠代表偏差因子標準數據的經驗關系進行編程計算,這些偏差因子關系式多是源于狀態方程,或直接通過回歸分析總結得到。
利用狀態方程擬合偏差因子數據進而總結經驗公式的方法是計算天然氣偏差因子的有效工具。氣體狀態方程有許多種,如Van der Waals方程[1-3]、RK方程[4-6]、SRK方程[7-9]、PR方程[10-12]等立方型狀態方程,以及Starling方程[13-14]、BWR方程[15-16]、BWRS方程[17-21]等維里狀態方程。維里狀態方程在氣體混合物偏差因子計算方法的發展過程中起到了重要的推動作用,較有代表性的有:Hall(1973)[13]在Carnahan-Starling(1969)硬球方程[14]的基礎上提出了一種迭代計算偏差因子的關系式,即HY方法;Dranchuk等人(1973)[22]利用BWR狀態方程擬合偏差因子數據[23]提出了一種8系數表達式,即DPR方法;Dranchuk和Abou-Kassem(1975)[24]則應用BWRS方程提出了一種11系數偏差因子計算式,即DAK方法。這3種方法是應用狀態方程計算天然氣偏差因子的經典方法,在一定范圍內它們均能比較準確地代表Standing-Katz圖版數據[23],其中DAK方法的計算精度最高,但其在高溫高壓下的計算誤差也稍大,存在改進的空間。為此,筆者基于改進的BWRS狀態方程提出一種新的偏差因子計算方法,以期更精確地確定天然氣偏差因子。
1 改進的BWRS狀態方程
Benedict等人(1940,1942)[15-16]提出了一種剩余功(residual work content)與密度、絕對溫度之間的經驗方程,給出了與之對應的狀態方程,即Benedict-Webb-Rubin方程,其表達式為方程(1)。
BWR狀態方程因其能比較準確地計算氣體的熱力學性質而得到了廣泛應用,例如,Dranchuk等人(1973)[22]利用BWR狀態方程擬合平滑處理后的Standing-Katz圖版[23]上的1 500個數據點,提出了DPR方法。后來,許多學者對BWR方程進行了修正和推廣,以期更加準確、有效地預測更大壓力和溫度范圍內的純物質及混合物的熱力學性質參數。其中,Starling(1970)[17-18]修正的BWR方程(即BWRS方程)頗具代表性,應用較為廣泛[19-21],其表達式為方程(2)。
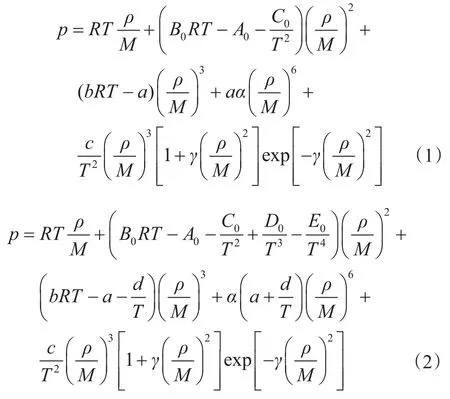
式中,p為壓力,Pa;R為摩爾氣體常數,8.3144598 J/(mol·K);T為溫度,K;ρ為密度,kg/m3;M為摩爾質量,kg/mol;B0、A0、C0、b、a、α、c、γ均為與狀態方程相關的系數;D0、E0和d為BWRS方程相較于BWR方程增加的3個系數。
BWRS狀態方程是基于統計力學攝動理論對BWR方程中的系數C0和a相關項作了修改而得到的。增加的3個系數D0、E0和d有助于擬合并預測流體在低溫及臨界區的熱力學參數(焓、熵、蒸氣壓等)。利用BWRS方程,Dranchuk(1975)[24]同樣應用DPR關系式所用的1 500個偏差因子數據點進行擬合,提出了DAK方法。由于狀態方程的改進,DAK方法比DPR(1973)方法具有更高的計算精度,但其在15≤ppr≤30 & 1.4≤Tpr≤2.8高壓范圍內的計算結果與Katz(1959)高壓偏差因子圖版之間的誤差稍大,仍可改進。胡建國(2013)[25]利用6 548組偏差因子數據對DAK方法的11個系數進行了修正,改善了高壓下的偏差因子計算精度,但這種修正在0.2≤ppr≤15 & 1.05≤Tpr≤3.0范圍內的計算結果卻與Standing-Katz圖版數據不符。
研究發現,對式(2)中的系數γ進行調整可明顯提高基于BWRS狀態方程的偏差因子計算方法的計算精度。為此,將式(2)改寫為
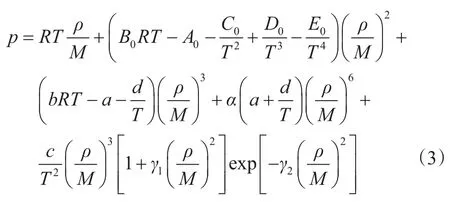
由真實氣體狀態方程得

在式(3)兩端同時乘以M/(ρRT),得
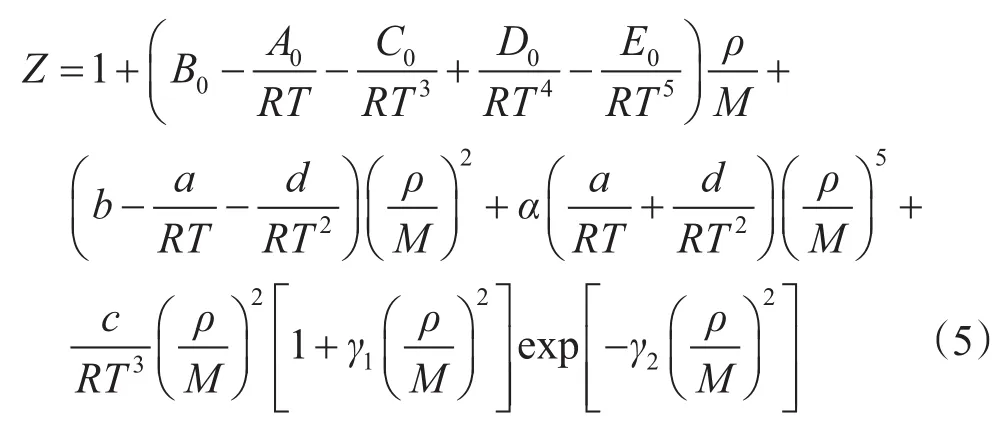
引入對比密度ρpr、對比溫度Tpr和對比壓力ppr
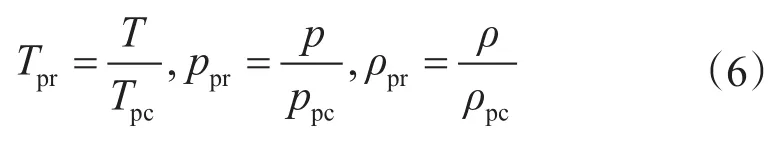
則式(5)可化為
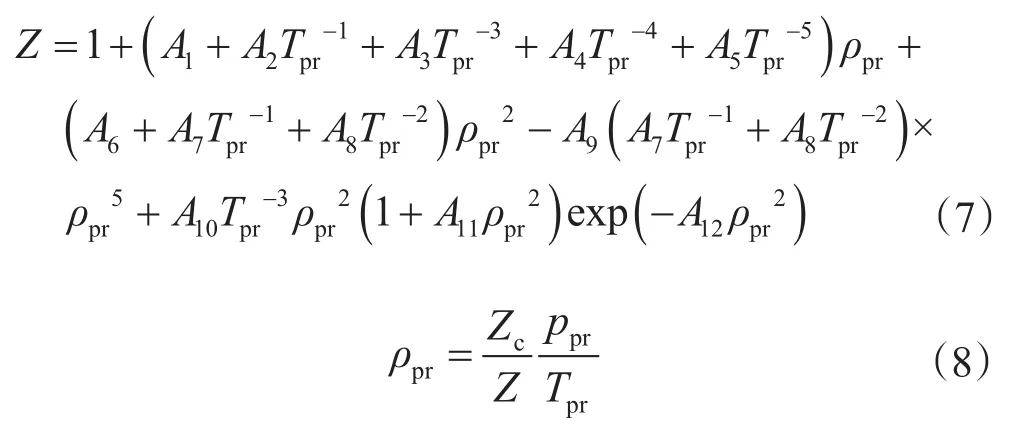
其中
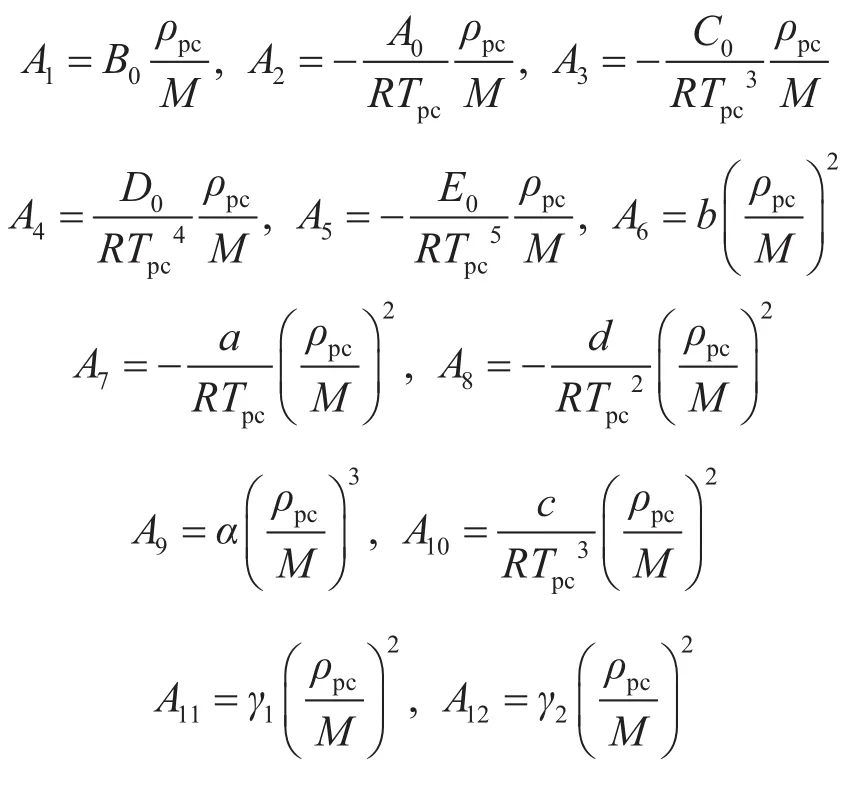
式中,γ1、γ2為改進的BWRS方程的系數;Z為氣體偏差因子;Tpr為(擬)對比溫度;ppr為(擬)對比壓力;Tpc為(擬)臨界溫度;ppc為(擬)臨界壓力;ρpr為(擬)對比密度;ρpc為(擬)臨界密度;Zc為臨界偏差因子,計算時一般取0.27。
式(7)和式(8)反映了偏差因子Z與Tpr、ppr和ρpr的隱式關系,相較于DAK方法,該關系式增加了一個系數,同樣可利用迭代法求解Z。
2 偏差因子計算方法
使用式(7)計算Z需要先確定A1~A12等12個系數的值。Poettmann(1952)[26]、Katz(1959)[27]及Smith(1990)[28]均發表了0.2≤ppr≤15 & 1.05≤Tpr≤3.0范圍內Standing-Katz圖版(圖1)數值化的標準偏差因子數據表(共297×20=5 940個數據點);Poettmann[26]數據表中的5個數據點疑似有誤(因為在這些點處,Z值發生了突變),作如表1修改。
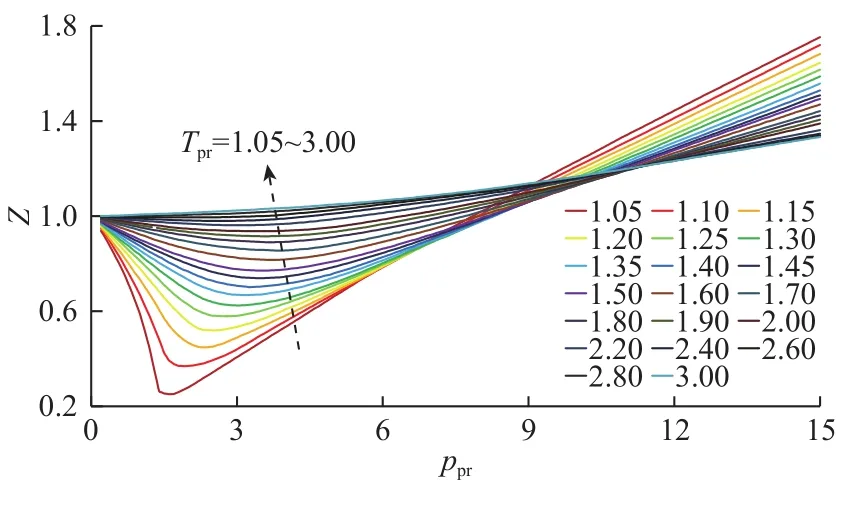
圖1 Standing-Katz 偏差因子圖版[23]Fig.1 Standing-Katz Z-factor chart[23]
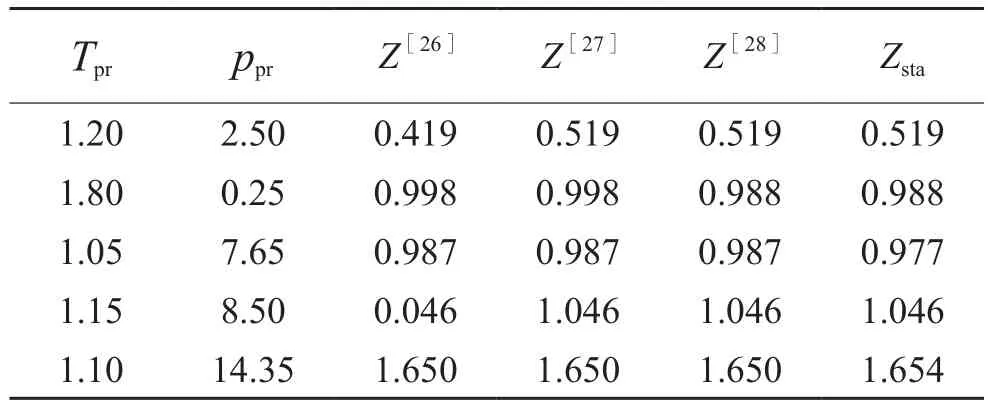
表1 5個偏差因子數據點的修改值Table 1 Modified values of 5 Z-factor data points
對于常用的壓力范圍,以Poettmann(1952)數值化的偏差因子數據作為標準;對于“15≤ppr≤30、1.4≤Tpr≤2.8”范圍內的Katz(1959)[27]圖版(圖2),同樣利用數值化處理結果作為參照依據(每條等溫線上對比壓力ppr每隔0.1取一個點,共151×8=1 208個數據點)。
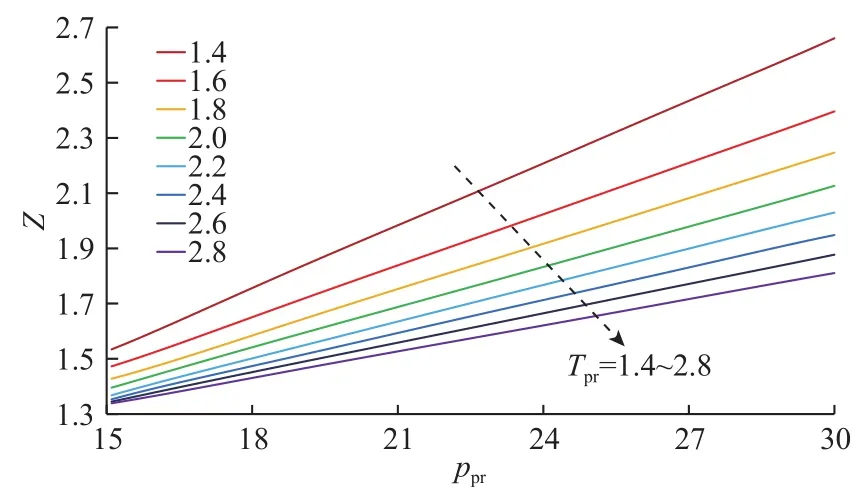
圖2 15 ≤ ppr ≤ 30 范圍內的Katz 圖版[27]Fig.2 Katz chart for 15 ≤ ppr ≤ 30[27]
為方便數據擬合,式(7)可寫為:
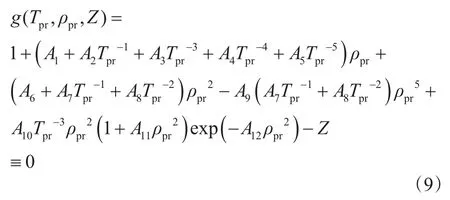
函數g(Tpr,ρpr,Z)以Tpr、ρpr、Z為自變量,且其函數值應恒為0;利用上述7 148組數據點分2個區擬合該函數,求滿足式(10)時各系數A1~A12的值,此過程可用Matlab中的非線性最小二乘回歸(nonlinear least squares regression)函數編程實現。各系數A1~A12的取值見表2。
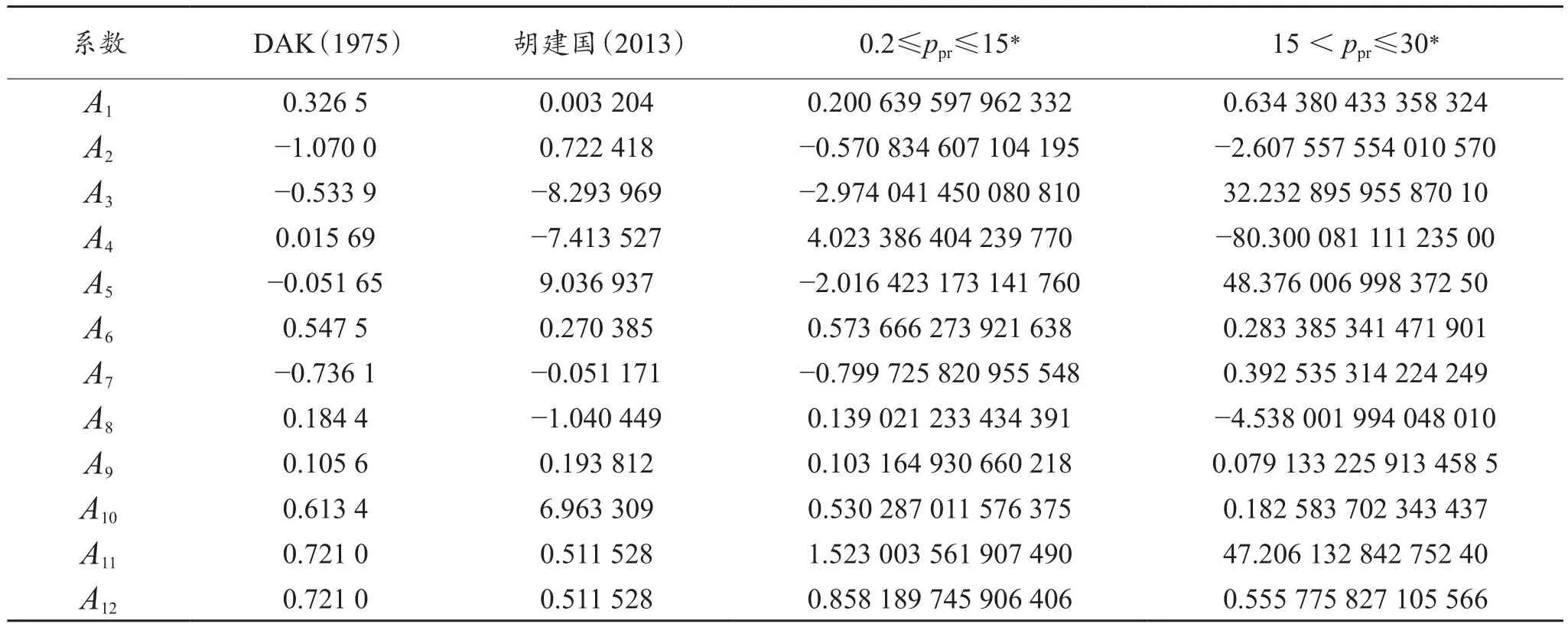
表2 改進BWRS狀態方程的系數Table 2 Coefficients of modified BWRS Equation
利用牛頓迭代法[29]求解偏差因子Z較為方便,可令函數f(ρpr)為
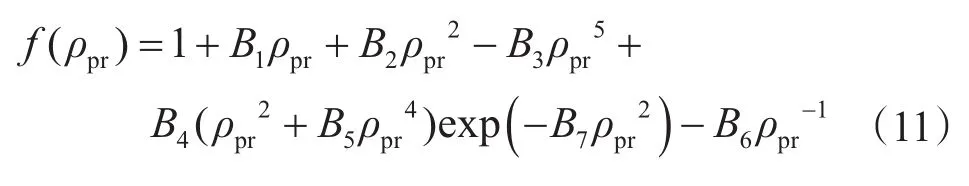
其中
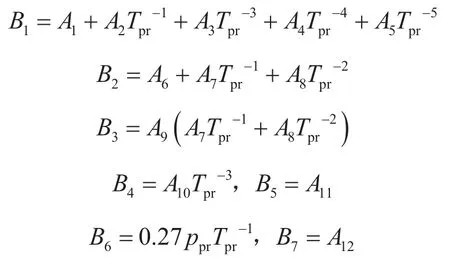
f(ρpr)關于ρpr的導數為
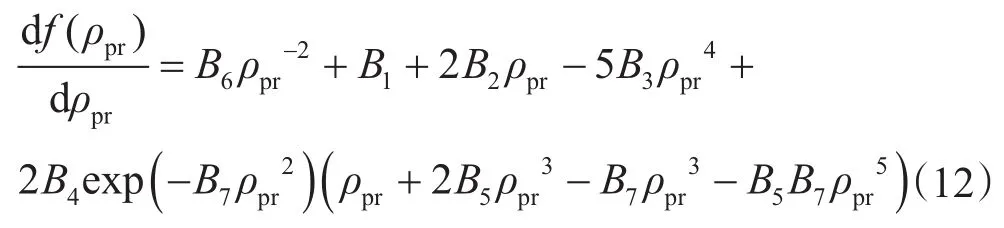
牛頓迭代公式為
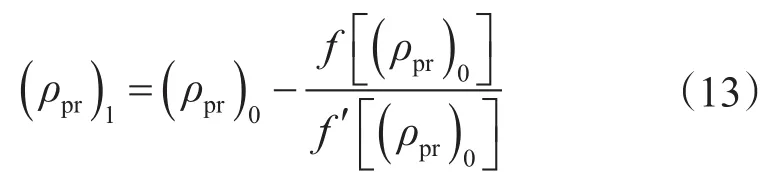
式中,(ρpr)0為上次計算的對比密度;(ρpr)1為本次得到的對比密度。
具體求解步驟如下:
(1)給定ppr、Tpr,設定最大迭代次數N和計算精度eps;
(2)令(ρpr)1=0.27ppr/Tpr,k=0;
(3)將(ρpr)1賦給(ρpr)0;
(4)利用式(13)得到對比密度(ρpr)1;k+1→k;
(5)比較(ρpr)1和(ρpr)0的絕對差,若k>N或abs[(ρpr)1-(ρpr)0]<eps,則迭代終止;否則,繼續步驟(3)~(5)。
(6)計算偏差因子,Z=0.27ppr/[Tpr(ρpr)1]。
3 計算結果對比
利用Standing-Katz圖版數值化的5 940組數據[26-28]和Katz(1959)圖版數值化的1 208組數據對表2中3種取值方法進行評價(平均絕對誤差記為AAE),0.2≤ppr≤15 & 1.05≤Tpr≤3.0范圍(中低壓區)內的計算誤差記為AAE1,15≤ppr≤30& 1.4≤Tpr≤2.8范圍(高壓區)內的計算誤差記為AAE2,總共7 148個數據點的計算誤差記為AAE3。
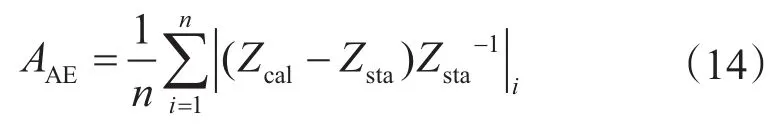
式中,Zcal為計算的Z值。
表3列出了這3種相關的偏差因子計算方法的平均絕對誤差;本文提出的12系數關系式的AAE1為0.382%,相較于原DAK方法,其計算精度提高了12.084%;而AAE2為0.205%,比DAK方法的計算精度高了79.041%;0.2≤ppr≤15 & 1.05≤Tpr≤3.0以及15≤ppr≤30 & 1.4≤Tpr≤2.8范圍內各等溫線的計算誤差見表4、5。
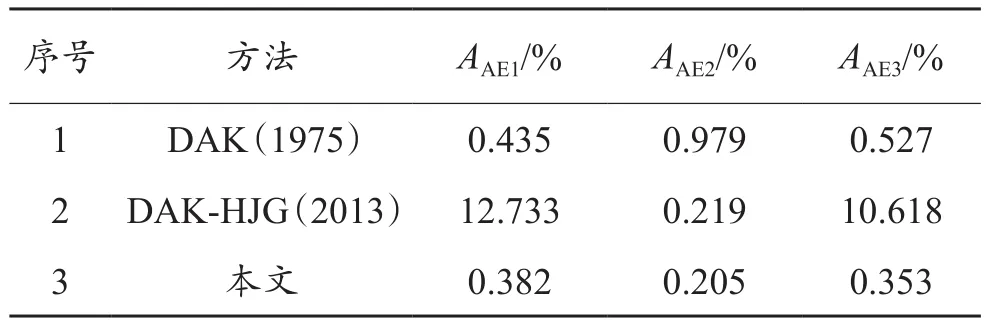
表3 誤差分析Table 3 Error analysis
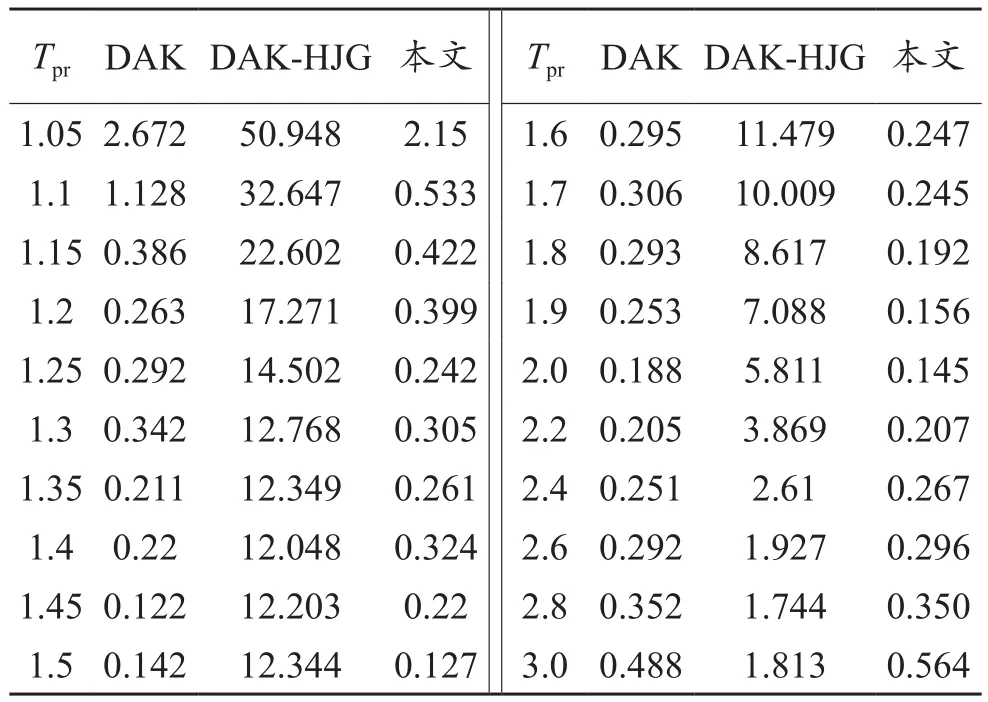
表4 0.2≤ppr≤15 & 1.05≤Tpr≤3.0范圍內各等溫線的平均絕對誤差 %Table 4 Average absolute error of each isothermal line for 0.2≤ppr≤15 & 1.05≤Tpr≤3.0
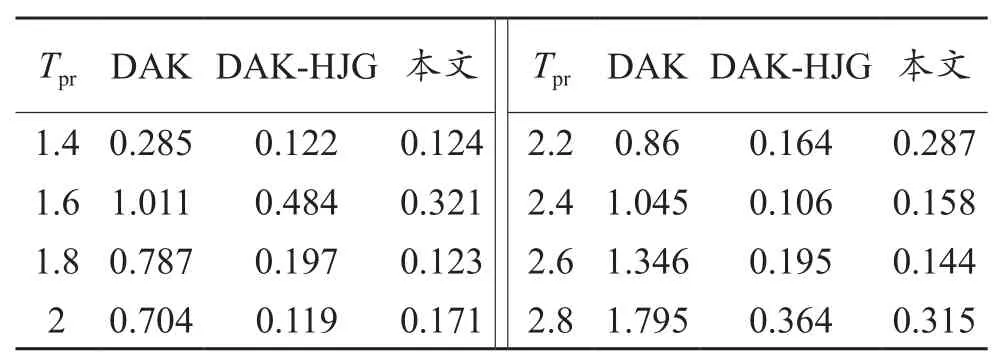
表5 15≤ppr≤30 & 1.4≤Tpr≤2.8范圍內各等溫線的平均絕對誤差 %Table 5 Average absolute error of each isothermal line for 15≤ppr≤30 & 1.4≤Tpr≤2.8
圖3、圖4統計了DAK(1975)[24]、DAK-HJG(2013)[25]和本文提出的新方法在中低壓和高壓范圍內的偏差因子計算誤差,其大小由顏色從藍到紅來體現。對于“0.2≤ppr≤15 & 1.05≤Tpr≤3.0”的中低壓情形,計算誤差以10%為界,圖3中缺失部分表示誤差大于10%的區域。同理,對于“15≤ppr≤30& 1.4≤Tpr≤2.8”的高壓情形,由于計算誤差整體較小,圖4只展示誤差小于2%的區域。
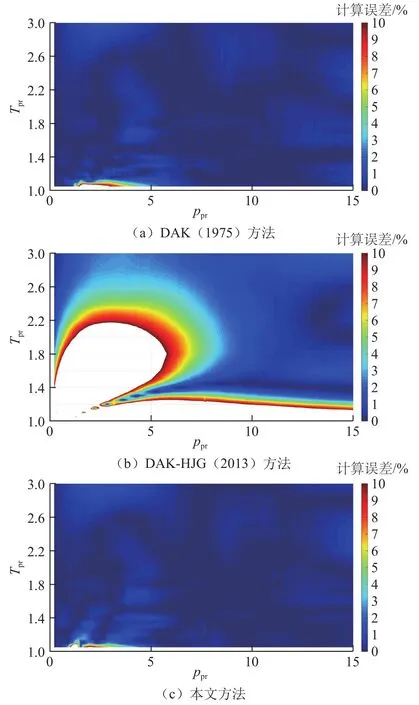
圖3 0.2≤ppr≤15 & 1.05≤Tpr≤3.0范圍內3種方法的誤差分布Fig.3 Error distribution for 0.2≤ppr≤15 & 1.05≤Tpr≤3.0 by three methods
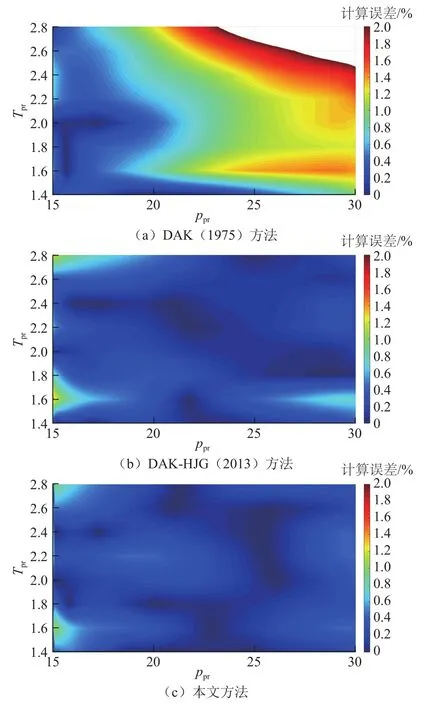
圖4 15≤ppr≤30 & 1.4≤Tpr≤2.8范圍內3種方法的誤差分布Fig.4 Error distribution for 15≤ppr≤30 & 1.4≤Tpr≤2.8 by three methods
對于中低壓區,DAK-HJG(2013)方法的缺失區域較大,藍色區域占比較低,其AAE1=12.733%,由此可見,該方法在0.2≤ppr≤15、1.05≤Tpr≤3.0范圍內并不適用;而DAK(1975)和新方法的計算精度較高(AAE1分別為0.435%、0.382%),但新方法誤差大于10%的區域更小,整體誤差也更小。
對于高壓區,DAK(1975)方法在高溫區域部分點的計算誤差大于2%(部分區域缺失),其平均絕對誤差也最大(AAE2為0.979%);而DAK-HJG方法和新方法的誤差較小(AAE2分別為0.219%和0.205%),但新方法的最大誤差更小(僅為1.091%)。
筆者認為BWRS方程中指數項中的γ與前一項的γ取值不相同時該方程能更準確地代表氣體(尤其是在高壓下)的性質;由于增加了一個系數,修正后的方程對于天然氣偏差因子數據的代表能力應更強。此外,本文使用了0.2≤ppr≤15 & 1.05≤Tpr≤3.0范圍內的5 940個數據點(對Poettmann發布的偏差因子標準數據[26]進行了更正)以及15≤ppr≤30 & 1.4≤Tpr≤2.8范圍內的1 208個數據點,偏差因子Z數據體更大,故新方法適用范圍更廣,計算精度更高。
4 結論
(1)基于改進的BWRS狀態方程和DAK方法導出了一種12系數偏差因子關系式,利用7 148組偏差因子數據結合非線性回歸分析確定了這些系數,提出了一種新的Z值確定方法。
(2)由于BWRS方程中指數項的改進,該方程能更準確地代表及預測氣體(尤其是在高壓下)的物理性質。
(3)由于偏差因子數據的合理性以及狀態方程的改進,新方法的計算精度更高。新方法在中低壓和高壓下的平均絕對誤差分別為0.382%、0.205%,這比原DAK方法的計算精度分別高出12%和79%;推薦使用范圍為:0.2≤ppr≤15 & 1.05<Tpr≤3.0以及15≤ppr≤30 & 1.4≤Tpr≤2.8。而胡建國修正的DAK方法只適用于高壓(15≤ppr≤30)的情形。

