基于奇異值分解的壓縮感知觀測矩陣優化算法

李　周，崔　琛

(國防科技大學 電子對抗學院，合肥 230037)(*通信作者電子郵箱17756587331@163.com)

0　引言

壓縮感知(Compressive Sensing, CS)[1-3]在采樣率遠小于奈奎斯特采樣率的條件下獲取信號的離散樣本，然后通過非線性優化算法重構出原始信號。重構信號所需的采樣率并不取決于信號的帶寬，而與信號的稀疏度密切相關，因此CS有效降低了信號獲取、存儲及傳輸的代價，引起了越來越多學者的關注。

信號的稀疏表示、觀測矩陣的構造、重構算法是CS理論中三個主要研究方向，其中觀測矩陣是影響壓縮感知性能的關鍵因素之一[4]。觀測矩陣構造的目的是如何采樣得到觀測值，并能從觀測值中重構出原始信號。文獻[5-7]對精確重構所需觀測矩陣的約束條件進行了研究：文獻[5]提出了零空間性質(Null Space Property, NSP)，但在存在噪聲的情況下NSP并不能保證信號的精確重構；文獻[6]提出了有限等距性質(Restricted Isometry Property, RIP)，但判斷觀測矩陣是否符合RIP需要計算觀測矩陣n列中任意組合的K列，即需要計算觀測矩陣各列的組合，實際用于觀測矩陣的分析非常困難；文獻[7]提出了相關性的概念，其含義是觀測矩陣與稀疏基之間的相關程度，通過降低相關性可以減少CS的重構誤差和精確重構原始信號所需的觀測數。

文獻[7]通過線性收縮Gram矩陣中絕對值大于限定閾值的非對角元來降低相關性，取得了較好的實驗效果。但是，該算法在收縮Gram矩陣時會改變矩陣的秩[8-9]；同時在求解觀測矩陣時需要求解稀疏基的逆矩陣，但由于稀疏基可能奇異，此時需要利用稀疏基的Moore-Penrose廣義偽逆來求解新的觀測矩陣，造成了算法中計算量大且精度受限的問題[4,8]。文獻[9]延續了文獻[7]之前的思路，不同之處在于增加了一個保留前一次矩陣優化信息的操作，其目的在于使每一次矩陣更新的變化量減少，該算法繼承了文獻[7]的缺點，同時需要根據經驗手動設置一個權重系數，用來衡量本次矩陣優化結果與前一次矩陣優化結果之間的比重。

文獻[10]提出將Gram矩陣非對角元素的平方和作為整體互相關系數，用來表示觀測矩陣的整體性能；在此基礎上，文獻[11]引入了α緊框架的概念，平均化Gram矩陣的非零特征值，減小了整體相關系數。但在由Gram矩陣求解觀測矩陣時，文獻[10-11]仍采用了求稀疏基Moore-Penrose廣義偽逆矩陣的做法，同樣造成了算法中計算量大且精度受限的問題。

針對現有算法從優化后的Gram矩陣求解觀測矩陣時出現的相關系數較大與需要求廣義偽逆矩陣的問題，本文借鑒了K-SVD(K-Singular Value Decomposition)算法中逐行更新優化目標矩陣的思想，在利用現有算法得到優化后的Gram矩陣的基礎上，提出了一種基于奇異值分解(Singular Value Decomposition, SVD)的觀測矩陣優化算法：該算法通過求解等價變換后的目標函數對觀測矩陣行向量的導數得到目標函數取極值時行向量的值，并通過對誤差矩陣進行奇異值分解在上述行向量的值中選出使得目標函數取最值時行向量的解析式，之后在每輪迭代中對觀測矩陣的每一行分別使用上述的行向量解析式進行優化。

1　觀測矩陣相關性和相應算法

1.1　觀測矩陣相關性

假定離散信號r∈Rl×h，若r中最多含有K個非零值且K≤h，那么r就稱作K-稀疏的。將K-稀疏的信號集合記為：

ΛK={r:‖r‖0≤K}

(1)

若r本身為非稀疏的，但可以經過一個稀疏基Ψ作如下變換：

r=Ψs

(2)

如果變換后的s符合‖s‖0≤K≤h，即r可以用已知的稀疏基中少量的元素線性表示，那么r也被稱作K-稀疏的。

CS理論的測量過程[1]可以表示為：

y=Φr=ΦΨs=Xs

(3)

其中：r為原始信號，Ψ∈Rn×h為稀疏基，s為變換后的稀疏信號，Φ∈Rm×n為觀測矩陣，XΦΨ稱為感知矩陣。

對于任意兩個不同的稀疏信號r1,r2∈ΛK，必須滿足Xr1≠Xr2，否則僅僅根據觀測值無法區分r1,r2，因此感知矩陣需要滿足一定的條件：對于任意K-稀疏的信號，只要其稀疏度K滿足下式，信號即可準確地恢復出來[12]。

(4)

其中μ(X)指X任意兩列xi和xj之間的內積絕對值的最大值[7]，計算公式如下：

(5)

然而μ(X)僅表示觀測矩陣與稀疏基之間列向量最大的相關性，是一種局部的相關性，因為在X只有某兩列的相關性比較大而其余各列之間相關性比較小的情況下，就會出現相關系數μ(X)很大而感知矩陣X的性能并不差的情況。

因此文獻[7]提出了表示總體相關性的t-平均相關性μt-av，定義為X所有列向量兩兩之間的內積絕對值中大于限定閾值t的部分的平均值，或者是X所有列向量兩兩之間的內積絕對值中最大的t%部分的均值，其定義式如下：

(6)

其中:gij為Gram矩陣G=XTX中的元素，gij為矩陣X的第i列xi與第j列xj的內積，Nav為Hav中的元素數，即Gram矩陣非對角元|gij|大于t的數目或者所有|gij|中最大的t%部分的元素數目。僅闡述μt-av為X任意兩列內積絕對值大于t的平均值時Hav的定義：

Hav={(i,j):gij>t,i≠j}

(7)

1.2　觀測矩陣優化的相關算法及問題分析

為降低X任意兩列的相關性，即減少Gram矩陣非對角元素的值，文獻[7]采用如下閾值函數對Gram矩陣G中絕對值大于限定閾值的非對角元進行線性收縮：

(8)

其中：t為閾值，γ為收縮因子。

(9)

其中：A=ΦΨ。在Ψ逆矩陣存在時，Φ=AΨ-1；但在稀疏基Ψ可能奇異導致其逆矩陣不存在時，需要利用稀疏基的Moore-Penrose廣義偽逆來求解觀測矩陣Φ=AΨ+，從而帶來計算量與精度的問題[4,8]。

文獻[6]的閾值函數只能使局部比較大的非對角元素減小。為整體減小Gram矩陣中的非對角元素，文獻[11]通過平均化Gram矩陣的非零特征值，使得矩陣非零特征值的平方和減小，降低了整體相關系數。但在由Gram矩陣求解觀測矩陣時，仍然需要求解稀疏基的廣義逆矩陣，故存在著與文獻[7]相同的問題[4,8]。

1.3　問題的解決思路

在現有算法優化Gram矩陣后，本文借鑒了文獻[13]提出的K-SVD算法中逐行優化目標矩陣的思想從優化后的Gram矩陣求解觀測矩陣。

K-SVD是一種通過逐行優化字典矩陣對信號進行稀疏表示的方法，具體目標為：

(10)

其中:Y為要表示的信號，D為所求的字典，X為稀疏矩陣。X與Y按列對應，表示D中的元素以xi為系數線性組合就可得到Y，而K-SVD的目的是在X和Y已知的情況下更新字典D滿足上述條件。

(11)

式(11)可以看作把第k個分量剝離后表達式會產生空洞，目的是找到一個新向量以更好地填補這個洞：假設除第k項外其余項是固定的，之后對Ek進行奇異值分解得到Ek=UΛVT，其中U和V的列矢量均是正交基，Λ是對角矩陣。若Λ的對角元素從大到小排列，則表示Ek的能量分量主軸在相應幾個正交方向上由大到小分配，取U的第一個列向量來表示di，取V的第一個列向量與Λ的第一個元素的乘積表示xi，至此完成了字典一個條目的更新。

2　觀測矩陣的優化算法

在利用現有算法得到優化后的Gram矩陣的基礎上，借鑒K-SVD算法中逐行更新優化目標矩陣的思想，本章利用稀疏基的奇異值分解對目標函數進行等價變換，通過求解等價變換后的目標函數對觀測矩陣行向量的導數得到目標函數取極值時行向量的值，并通過對誤差矩陣進行奇異值分解在上述行向量的值中選出使得目標函數取最值時行向量的解析式，最后利用所求出的行向量解析式逐行迭代優化觀測矩陣。

2.1　觀測矩陣行向量的優化

(12)

假設稀疏基Ψ的秩為NΨ，其奇異值分解為：

(13)

將奇異值分解式代入目標函數中，可得：

(14)

根據F范數的酉不變性，在式(14)中左乘VΨT，右乘VΨ，同時設ΦUΨ其中為的前NΨ列。設其中為的前NΨ行與前NΨ列，將和代入式(14)可得：

(15)

由式(15)易得：

(16)

(17)

(18)

式(18)對ωj求導可得：

(19)

導數置0便可得到一系列極值點：

(20)

易得：

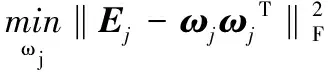
(21)

(22)

2.2　觀測矩陣的迭代優化算法

在現有算法得到優化后的Gram矩陣的基礎上，本小節利用2.1節求出的觀測矩陣行向量的解析式，采用逐行更新的方法優化觀測矩陣。

輸入初始觀測矩陣Φ∈Rm×n，離散傅里葉變換基Ψ∈Rn×h，迭代次數Iter，退出閾值μ0;

輸出觀測矩陣。

fork=1:Iter

1)

2)

forj=1:m

end for

3)

4)

計算，若μt-av與上一輪迭代的μt-av之差小于μ0則退出循環，否則轉至1)繼續循環

end for

3　實驗結果及其分析

本文在Matlab平臺上對算法進行仿真實驗，仿真選擇高斯隨機矩陣作為初始觀測矩陣，離散傅里葉變換基作為稀疏基，比較文獻[7]所提的算法CSElad、文獻[11]所提的算法CSTsiligianni和經文獻[11]中的方法優化Gram矩陣后使用本文所提的算法CSImproved-Tsiligianni在相關性、重構誤差和運行時間三方面的性能。

仿真中相關參數如下：m=30，n=l=100，稀疏度K=10，迭代次數Iter=100。Gram矩陣收縮變換時非對角線的限定閾值t=30%，收縮因子γ=0.5，CSImproved-Tsiligianni的退出閾值μ0=10-2。為減少隨機性對實驗結果造成的影響，每次仿真均為1 000次的蒙特卡羅仿真。

3.1　相關性

仿真實驗一 ：CSElad、CSTsiligianni和CSImproved-Tsiligianni都是迭代進行的算法，去除改進算法第四步迭代退出的步驟，將三種算法每次迭代時Gram矩陣的t-平均相關性μt-av進行對比，可以看出在各個算法迭代時t-平均相關性的變化趨勢，進而對比出三種算法在t-平均相關性這一方面的優劣性。t-平均相關性μt-av中的參數t=20%，其含義是Gram矩陣非對角元中最大的20%部分的均值。

圖1　不同算法的μt-av隨迭代的變化Fig. 1　Changes in μt-av of different algorithms with iterations

由圖1可知，隨著迭代的進行，CSImproved-Tsiligianni的μt-av逐漸減小而趨于穩定，而CSElad和CSTsiligianni的μt-av變化范圍較大;同時，改進算法的μt-av比改進之前的算法小，這是由于改進算法利用優化后的觀測矩陣行向量的解析式逐行優化觀測矩陣。

3.2　重構誤差

(23)

仿真實驗二：觀測次數m對壓縮感知的重構誤差的影響。仿真了觀測次數m從25增加到45時三種算法重構誤差的變化情況，如圖2所示。可以看出，在給定信號長度和稀疏度的前提下，m越大，重構誤差越小；m越小，重構誤差越大。

圖2　觀測次數變化時三種算法的MSE變化情況Fig. 2　Changes in MSE of three algorithms with observation number

仿真實驗三：稀疏度K對算法的重構性能的影響。為了得出稀疏度K對各個算法重構性能的影響，仿真稀疏度K由10變化到20時三種算法的MSE的變化情況，如圖3所示。可以看出，在給定觀測次數和信號長度的前提下，稀疏度越高，重構誤差越大。

圖3　稀疏度變化時三種算法的MSE變化情況Fig. 3　Changes in MSE of three algorithms with signal’s sparsity

由仿真實驗二與三可知在K或m變化時CSImproved-Tsiligianni的MSE小于CSElad和CSTsiligianni，這是由于CSImproved-Tsiligianni產生的觀測矩陣與稀疏基的相關性小于CSElad和CSTsiligianni，可以更好地保持不同K稀疏向量之間的距離。

3.3　運行時間

為了研究本文所提算法的復雜度，該仿真實驗統計CSImproved-Tsiligianni優化觀測矩陣所需的運行時間，并與CSElad和CSTsiligianni的運行時間進行比較。雖然算法的運行時間不能嚴格地定義算法復雜度，但仍可以在一定程度上對算法的復雜度作出描述。仿真環境為2.53 GHz英特爾i5四核處理器、4 GB內存Windows 10系統下的Matlab R2014a。圖4給出了各算法在信號長度l和觀測次數m變化時相應的運行時間。

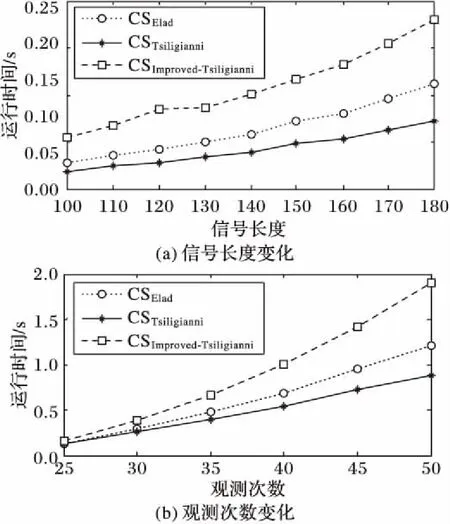
圖4　三種算法的運行時間對比Fig. 4　Running time comparison of three algorithms

由圖4可知信號長度和觀測次數增加時算法的運行時間隨之增加，其中CSElad和CSTsiligianni的運行時間小于CSImproved-Tsiligianni的運行時間，這是因為CSImproved-Tsiligianni在優化觀測矩陣時對每一行均采用奇異值分解來求解優化后的行向量，而奇異值分解耗時是較長的。不過相對于在相關性與重構誤差方面的優勢而言，CSImproved-Tsiligianni增加的運行時間還是可以接受的。

4　結語

本文對壓縮感知中觀測矩陣的優化問題進行研究，借鑒K-SVD算法中逐行更新目標矩陣的思想，在現有算法得到優化后的Gram矩陣基礎上，提出了一種基于奇異值分解的觀測矩陣優化算法。仿真結果表明：在可接受的運算量下，本文所提算法在觀測矩陣與稀疏基的相關性方面優于改進前的算法，從而提高了重構精度。如何優化閾值函數來構造性能更優的Gram矩陣是下一步的研究方向。

參考文獻:

[1]CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[2]DONOHO D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[3]CANDES E J, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies? [J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.

[4]王強,張培林,王懷光,等.壓縮感知中測量矩陣構造綜述[J].計算機應用,2017,37(1):188-196. (WANG Q, ZHANG P L, WANG H G, et al. A survey on the construction of measurement matrices in compressive sensing [J]. Journal of Computer Applications, 2017, 37(1): 188-196.)

[5]COHEN A, DAHMEN W, DEVORE R. Compressed sensing and best k-term approximation [J]. Journal of the American Mathematical Society, 2009, 22(1): 211-231.

[6]CANDES E J, TAO T. Decoding by linear programming [J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215.

[7]ELAD M. Optimized projections for compressed sensing [J]. IEEE Transactions on Signal Processing, 2007, 55(12): 5695-5702.

[8]鄭紅,李振.壓縮感知理論投影矩陣優化方法綜述[J].數據采集與處理,2014,29(1):43-53. (ZHENG H, LI Z. Survey on optimization methods for projection matrix in compress sensing theory [J]. Journa1 of Data Acquisition and Processing, 2014, 29(1): 43-53.)

[9]XU J, PI Y, CAO Z. Optimized projection matrix for compressive sensing [J]. EURASIP Journal on Advances in Signal Processing, 2012, 2010: Article No. 43.

[10]趙瑞珍,秦周,胡紹海.一種基于特征值分解的測量矩陣優化方法[J].信號處理,2012,28(5):653-658. (ZHAO R Z, QIN Z, HU S H. An optimization method for measurement matrix based on eigenvalue decomposition [J]. Signal Processing, 2012, 28(5): 653-658.)

[11]TSILIGIANNI E, KONDI L P, KATSAGGELOS A K. Use of tight frames for optimized compressed sensing [C]// Proceedings of the 20th European Signal Processing Conference (EUSIPCO). Piscataway, NJ: IEEE, 2012: 1439-1443.

[12]DONOHO D L, ELAD M. Optimally sparse representation in general (nonorthogonal) dictionaries via1minimization [J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 100(5): 2197-2202.

[13]AHARON M, ELAD M, BRUCKSTEIN A.rmK-SVD: an algorithm for designing overcomplete dictionaries for sparse representation [J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[14]ABOLGHASEMI V, FERDOWSI S, SANEI S. A gradient-based alternating minimization approach for optimization of the measurement matrix in compressive sensing [J]. Signal Processing, 2012, 92(4): 999-1009.

[15]KWON S, WANG J, SHIM B. Multipath matching pursuit [J]. IEEE Transactions on Information Theory, 2014, 60(5): 2986-3001.