自由運動曲率公式修整
——《自由運動論》在實際中的應用(33)
咸立德
(曲阜市書畫社,山東 曲阜 273100)
本文依據《自由運動論》的理論,重新綜合性總結了關于自由運動物體的運動規律的完整描述,同時給出了符合自由運動規律的自由運動曲率公式,而且公式是可以等效于一般受迫圓周運動的物理規律,公式可適用于宏觀和微觀領域的自然規律的相關預測。
一、自由運動曲率公式修整
在《自由運動論》中只是分章節分別描述了物體運動曲率和其它幾個物理量的關系。當綜合起來考慮的話。可以總結為:物體的運動曲率(K)和物體質量(m)成正比,和物體密度(ρ)成正比,和物體自轉速度(W)的平方成正比,和運動速度(V)的平方成反比。
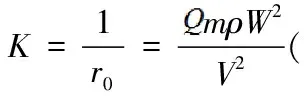
二、圓周運動和自由運動曲率公式的等效性
自由運動曲率公式也無非就是從多個物理量對運動的影響的角度上描述了物體做圓周運動的規律。其中部分規律是可以等效于現有的圓周運動規律的。就是在不考慮物體自轉速度、密度對曲率的影響,只考慮運動速度時,曲率運動公式中的運動速度對運動的影響,也是可以等效與于圓周運動的速度對運動的影響的。如圖1所示。
由圓周運動規律可知。
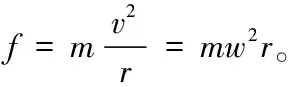
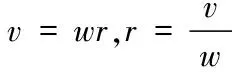
當物體脫離受迫圓周運動的向心力后,并不會做直線運動,因為物體仍具有公轉一周自轉一周的自轉速度W的慣性,和公轉速度v的慣性。在自轉導致的曲動力作用下仍然做以曲率半徑為r0的圓周運動。即曲動力f0可以等效于向心力f。
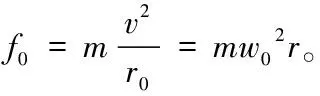
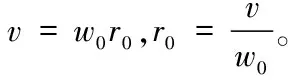
把v=wr帶入(2)式
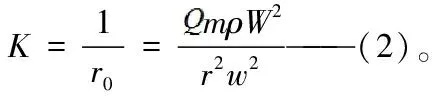
把v=w0r0帶入(2)式
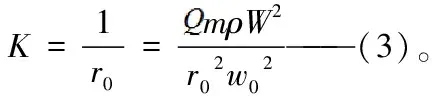
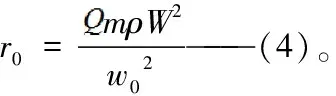
由(2)(3)式可知,受迫圓周運動的運動速度可以等效于自由運動曲率中的運動速,但是其曲率半徑r和r0是不同的,公轉角速度w和w0是不同的。且有:r
當自由運動在曲率半徑不變的前提下等效于受迫圓周運動時,就是當物體做曲率半徑為r,公轉角速度為w1的自由運動時,物體必須增大其自轉速度為W1,使其曲動力增大,相當于,受迫圓周運動的向心力由曲動力來提供。
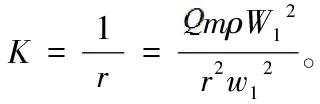
根據《自由運動論》的理論,在物體的速度許可范圍內,物體的總能量等于自轉能和動能之和,增大自轉速度會使運動速度減小,所以在曲率半徑相等的前提下等效時,自由運動的公轉角速度w1和受迫圓周運動的公轉角速度w也不同,且有:W1>w>w1
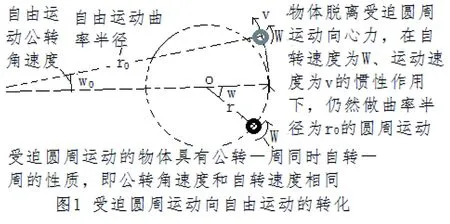
圖1
三、曲率公式在不同維度上的應用
(一)原始質量和星系的虛空中心的關系
以地球系為例,公式可以分別推算地球和月球在地球系里的公轉軌道。結合《<自由運動論>的宇宙學原理》第四節的論述,一個較小的天體繞著一個較大的天體公轉是相對的,事實上都是繞著一個虛空的中心在公轉而已。這個虛空的中心就是原始質量天體的存在時的位置。就是月球無異于在原始天體上人工發射了一個巨大的人造衛星。如圖2所示:
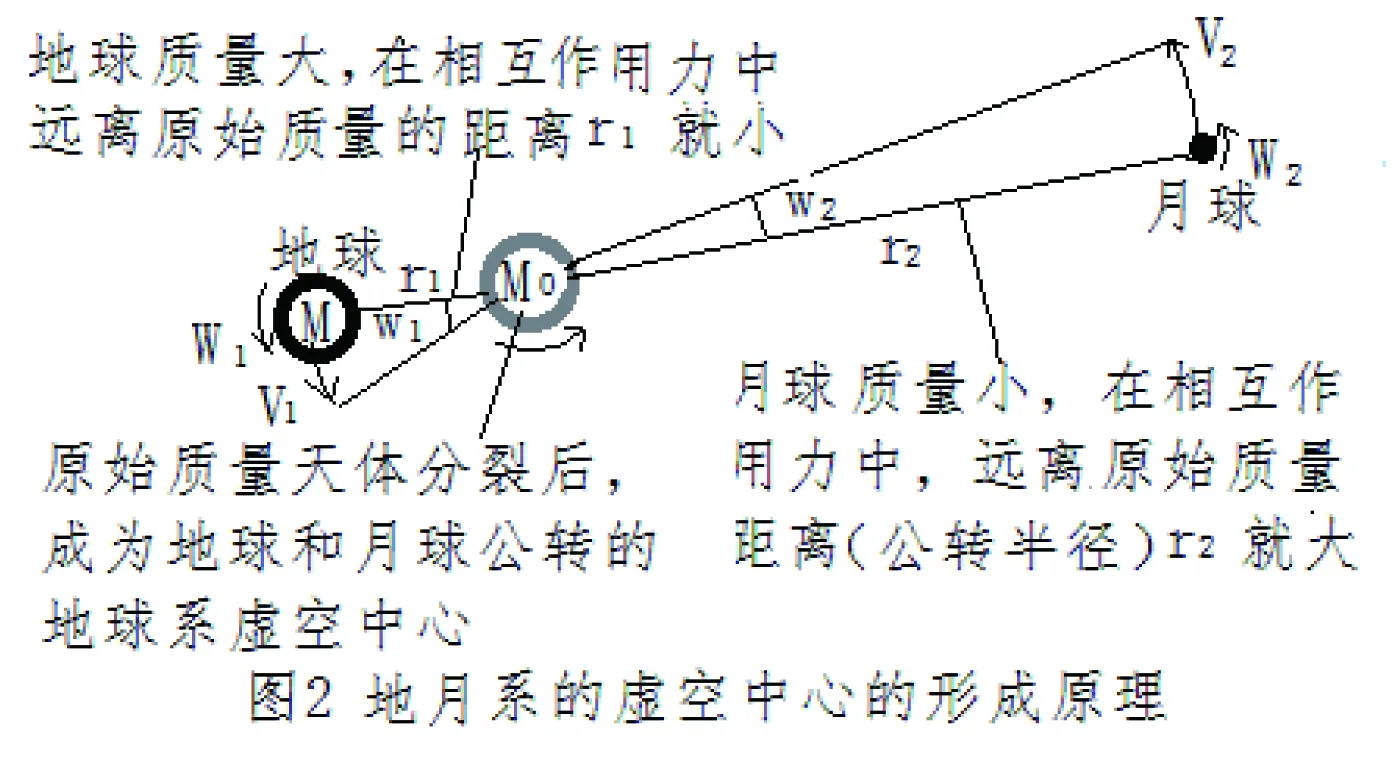
圖2
設原始天體質量為M0。膨脹分裂出一個月球后的地球質量為M,自轉速度為W1,公轉角速度為w1,月球質量為m(M0=M+m),自轉速度為W2,公轉角速度為w2.
設:地球的運動曲率為K,月球運動曲率為k。根據公式(3),
在地球系中有:
公式(5)(6)分別表達了地球和月球再地球系中的運動性質。由于地球和月球的公轉角速度w1和w2不同,所以,地球和月球的距離是可變的。設地球和月球的距離為r′。
有:r2-r1>r′ 公式(5)、(6)只是描述了地球和月球在地球系中的運動性質,根據《《N維空間論》續》的理論,要考慮在更高維度上的太陽系里的運動性質。就要考慮整個地球系的運動性質。比如地球系的自轉速度是由地球和月球在地球系里的公轉角速度來決定。運動速度要考慮地球系繞太陽的公轉速度,質量也是要考慮地球和月球的總質量等。如果把地球在地球系的運動視為一維運動,那么,地球在太陽系中就是二維運動。單獨考慮地球(或者月球)在太陽系里的二維運動性質會較為復雜,比如地球的二維上的自轉速度應該是地球在地球系里的公轉角速度等。 本文繼續以數學原理,利用自由運動曲率公式表達了星系都具有一個虛空的中心的客觀事實。通過對《自由運動論》理論中的自由運動曲率公式的修整,公式(1)、(3)基本可以描述宏觀和微觀的運動規律。 傳統理論認為人造同步衛星軌道與衛星質量無關,但是《自由運動論》的理論以及本文自由運動曲率公式表明,由于衛星軌道半徑和衛星質量成反比,按傳統理論發射衛星進入預測軌道后,較大質量的衛星會向著較小軌道上漫漫演化,甚至出現重新掉落到地面上的情況。公式(4)表明,衛星在公轉角速度不變(同步)的前提下,質量越大,軌道半徑就得越大。所以,依據自由運動曲率公式,質量較大的同步衛星軌道半徑要較大才能符合衛星運動性質。 在《關于自由落體的探討》一文中,只從《自由運動論》的理論作為基礎,分析了同等高度的質量大的物體先落地的原理。 事實上,地球表面附近的物體在做自由落體時,其運動也是符合《自由運動論》所描述的運動性質,自由運動曲率公式表明,質量較大的物體的落體(運動)軌道曲率較大,相對于地面觀察者的加速度就較大。所以,相對于地面觀察者,同等高度的物體在自由落體時,質量大的先落地才是符合客觀規律的。 本文依據《自由運動論》修整了一個完整的自由運動曲率公式。公式(1)(3)也是可以應用到微觀領域的。就是結合《論光的可變性》及《紅移現象的形成原理》,公式可以預測光粒子在大尺度上的公轉軌道半徑,同樣也可以預測光粒子在碰撞中產生巨大自轉速度,運動曲率急劇增大而形成復粒子后的極小的軌道半徑。所以自由運動曲率公式具有普適性。 參考文獻: [1]咸立德.自由運動論[c].2016首屆全國智慧城市建設高峰論壇論文集,2016. [2]咸立德.《自由運動論》的宇宙學原理[c].2016首屆全國智慧城市建設高峰論壇論文集,2016. [3]咸立德.陀螺儀進動原理——《自由運動論》在實際中的應用(17)[J].祖國,2014(09):92-93.(二)曲率公式在不同維度上的應用
四、自由運動曲率公式的意義
(一)在發射衛星問題上的指導意義
(二)對地球表面自由落體的同時性問題的糾正
五、自由運動曲率公式的普適性
六、結論

