提高三元肥效模型建模成功率的主成分回歸技術研究*

李 娟 章明清? 許文江 孔慶波 姚寶全

（1 福建省農業科學院土壤肥料研究所，福州 350013）

（2 福建省亞熱帶植物研究所，福建廈門 361000）

（3 福建省農田建設與土壤肥料技術推廣總站，福州 350003）

肥料效應函數是實現計量施肥的主要技術手段之一，其中，二次多項式是研究和應用最多的肥效模型［1-4］。但在施肥實踐中，應用普通最小二乘法（OLS）建立的二元或三元二次多項式肥效模型出現大量的非典型式［5-7］，諸如“最高產量”不高、“最佳產量”不佳、模型一次項系數為負數或二次項系數為正數、推薦施肥量遠外推等令人困惑的異常結果。針對肥效模型在應用中存在的問題，國內外學者就肥效模型選擇與其適用性［8-10］、試驗設計與參數估計方法［11-13］、類特征肥效模型構建［14-16］及非典型式推薦施肥優化方法［13］等方面進行了深入研究，提出了諸多改進措施，但對肥效模型設定本身是否存在問題及其應對方法則鮮見研究報道［4］。當前廣泛應用的“3414”設計方案的田間試驗結果，既使采用蒙特卡洛（Monter Carlo）建模法［13］，二元和三元二次多項式典型肥效模型的比例也僅有56.7%和37.3%，這種狀況嚴重制約了肥效模型的計量精確性和應用價值。

初步研究［4］表明，二次多項式肥效模型存在嚴重的多重共線性，制約了OLS法回歸建模的有效性。為此，本研究利用福建省近年來 “3414”試驗設計方案完成的早稻氮磷鉀田間肥效試驗結果，探討三元二次多項式肥效模型多重共線性診斷方法，以及主成分回歸（PCR）技術與其在消除多重共線性危害上的應用效果，旨在為提高氮磷鉀田間肥效試驗的建模成功率提供一種新方法。

1　材料與方法

1.1　早稻氮磷鉀“3414”田間肥效試驗資料的收集整理

近年來，福建省在水稻測土配方施肥工作中，在福州市、寧德市、南平市、三明市、龍巖市、莆田市、漳州的龍海市以及平和縣、泉州的南安市等水稻主產區，土肥技術力量較強的主要項目縣的早稻上先后完成了171個氮磷鉀田間肥效試驗。這些試驗均采用“3414”設計方案［17］，即：（1）N0P0K0；（2）N0P2K2；（3）N1P2K2；（4）N2P0K2；（5）N2P1K2；（6）N2P2K2；（7）N2P3K2；（8）N2P2K0；（9）N2P2K1；（10）N2P2K3；（11）N3P2K2；（12）N1P1K2；（13）N1P2K1；（14）N2P1K1。其中，“0”水平表示不施肥，“2”水平為試驗前的當地氮磷鉀推薦施肥量，“1”水平和“3”水平的施肥量分別為“2”水平的50%和150%。根據肥效模型建模過程中可能出現的未達統計顯著水平、典型肥效模型和三種不同形式的非典型肥效模型［7］等幾種類別，本研究選擇7個代表性早稻試驗結果（選擇依據主要是：根據普通最小二乘法建立三元肥效模型可能出現的幾種情形，在兼顧主要稻田土壤類型基礎上，分別選擇了OLS法未通過顯著性檢驗的1個代表性試驗點、OLS法產生的3種不同類型非典型式的3個代表性試驗點、OLS法為典型式的3個代表性試驗點）來探討三元二次多項式肥效模型的多重共線性診斷方法及其主成分回歸技術，并利用171個早稻氮磷鉀田間肥效試驗結果評價主成分回歸的應用效果。這7個試驗點涵蓋了灰泥田、黃泥田和灰沙田等福建稻田的主要土壤類型，采用常規方法［18］測定的土壤理化性狀（表1）也大致反映了各肥力指標的主要變化范圍。7個代表性試驗點N2P2K2處理的施肥量見表1，相關試驗產量見表2。供試水稻品種采用當地大面積種植的良種，試驗設計方案和田間管理措施與文獻［17］相同。

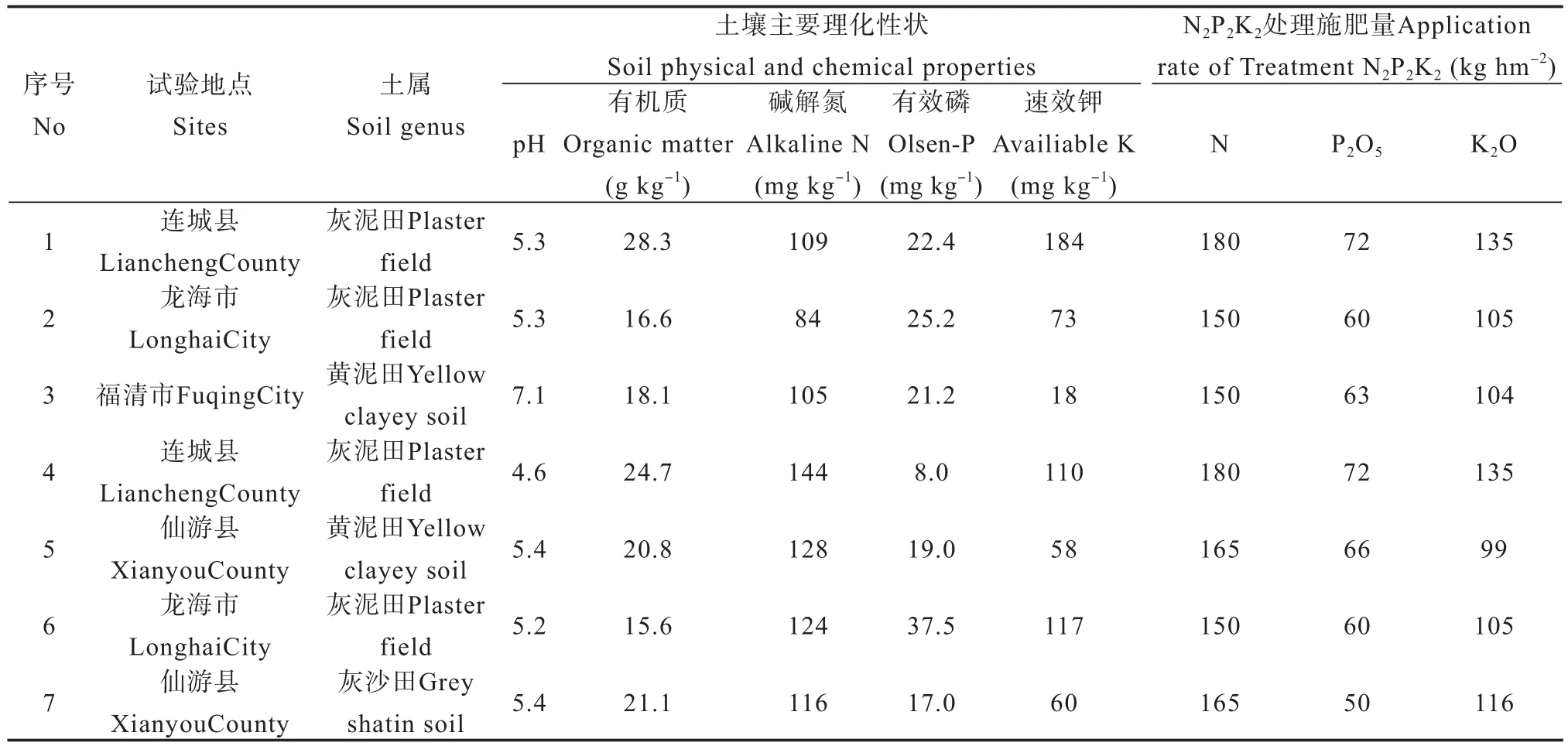
表1　早稻7個代表性試驗點土壤主要理化性狀及N2P2K2處理施肥量Table 1　Main physical and chemical properties of the soils in the seven representative experiment sites and fertilizer application rate of their Treatment N2P2K2

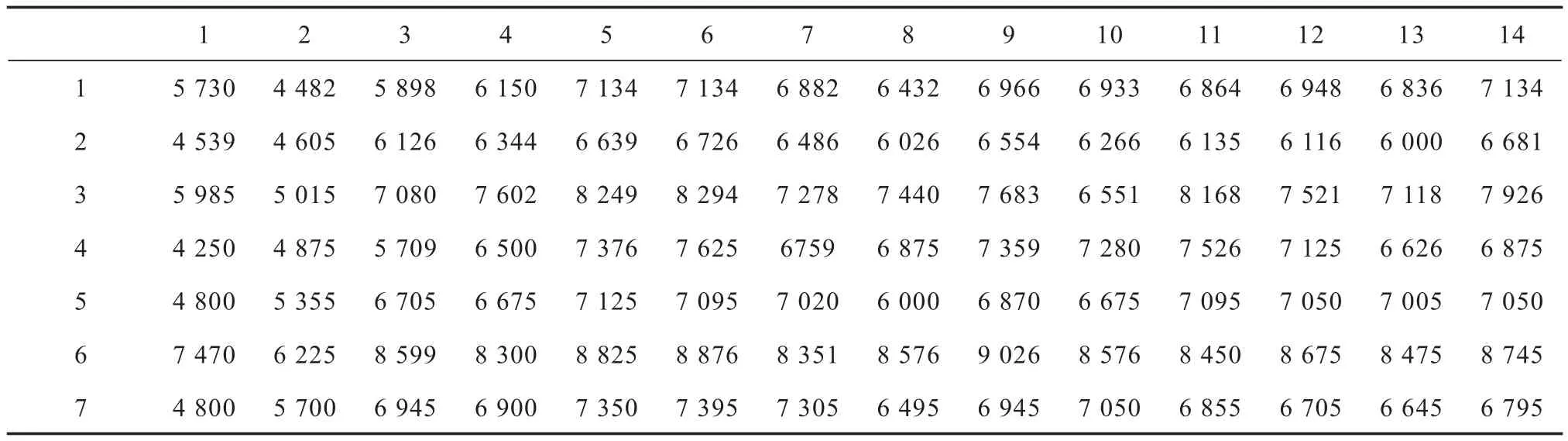
表2　早稻7個代表性試驗點各施肥處理的稻谷產量Table 2 Early rice yields in the seven representative trial sitesrelative to treatment(kg hm-2)

1.2　多項式肥效模型的多重共線性診斷方法

假設三元二次多項式肥效模型的數學形式如下：

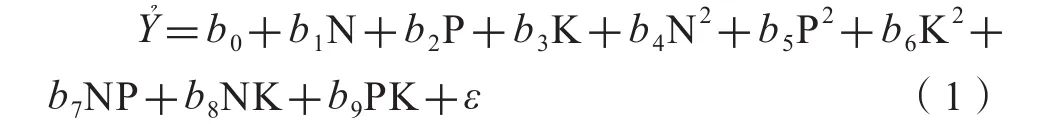
式中，N、P、K分別表示N、P2O5和K2O施肥量，kg hm-2；ε為擬合殘差，kg hm-2；Y為擬合產量，kg hm-2。在應用OLS回歸分析時，根據“3414”設計方案14個施肥處理的氮、磷、鉀施肥量與式（1）模型對應的9個回歸變量N、P、K、N2、P2、K2、NP、NK和PK可組成一個試驗設計矩陣X：

回歸變量： N P K N2P2K2NP NK PK

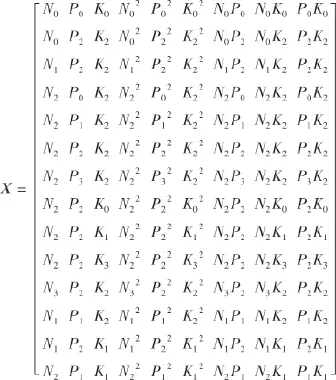
矩陣X共有14行和9列，每一行表示一個試驗處理，每一列表示一個回歸變量。在回歸分析的經典理論中，假設式（1）模型的9個回歸變量在兩兩之間不存在線性相關［19］。但在實際問題中，這些回歸變量之間總是會存在一定程度的相關性。在數學上，如果存在某些常數c1、c2…c9與相應各回歸變量的線性組合等于常數c0這一關系近似成立，則表示變量間存在多重共線性。因此，一個常用但不完全合適的共線性度量方法是樣本相關系數平方即r2［20］。精確共線性對應于r2=1，非共線性對應于r2=0。當r2越接近于1，近似共線性就越強。

度量多重共線性嚴重程度的一個重要指標是方陣XTX的條件數［19-20］，即：

式中，k為條件數，λmax、λmin分別為方陣XTX的最大特征值和最小特征值。一般應用經驗認為，若k＜100，則多重共線性的程度很小；若100≤k≤1000，則存在中等強度的多重共線性；若k＞1000，則存在嚴重的多重共線性。

多重共線性的另一個重要診斷指標是方差膨脹因子（VIF）［20］，即：

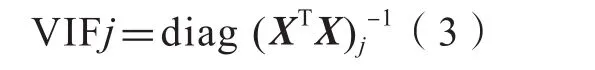
式中，(XTX)-1表示方陣XTX的逆矩陣，其中，X矩陣中的數據需事先進行標準化處理；diag表示取矩陣的對角線元素，j表示第j個回歸系數（j=1，2…9）。模型中各個回歸系數的VIF度量了回歸變量之間的相關性對該項回歸系數方差的影響，一個或更多個較大的VIF就表明存在多重共線性。一個經驗法則［20］認為，當VIF超過5或10時，就表明回歸模型存在嚴重的多重共線性。

1.3　多項式肥效模型的主成分回歸分析

當多項式肥效模型存在嚴重多重共線性時，一個有效解決辦法是重構回歸變量，使之成為無線性相關的新變量。主成分分析為重構回歸變量提供了可靠的數學方法，它將三元二次多項式肥效模型的9個回歸變量轉換成互不相關的9個主成分，然后選擇合適的幾個主成分進行OLS回歸分析。

因此，從試驗處理的原始施肥量數據出發，計算試驗設計矩陣X的協方差矩陣S，然后求取S矩陣的特征值和特征向量。對式（1）而言，特征值共有9個，從大到小排列為λ1、λ2…λ9，與之對應的特征向量為q1、q2…q9，每個q均為長度為9的列向量。設向量x= (N, P, K, N2, P2, K2, NP, NK, PK)T，則9個主成分的矩陣Z表達式為：

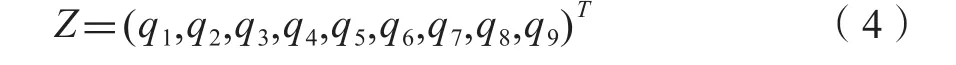
描述某個回歸變量Xj與某個主成分Zi相關程度的樣本相關系數計算式［21-22］為：

r的平方即為決定系數。若r2(Xj,Zi)數值大，就表明第i個主成分主要反映了第j個回歸變量的信息，其結果可用于解釋各個主成分的專業含義。

因此，應用中可根據各個主成分對試驗設計矩陣的方差貢獻大小，選用適當的主成分個數結合14個試驗處理產量結果進行OLS回歸分析，并進行相應的統計檢驗，這種方法稱為主成分回歸。

1.4　多重共線性診斷和主成分回歸的計算機實現

本研究采用MATLAB軟件進行多重共線性診斷和主成分回歸分析。在多重共線性診斷中，回歸變量間的相關系數計算調用corrcoef功能函數；方陣XTX的條件數、逆矩陣和VIF計算分別調用cond、inv等功能函數；X矩陣的協方差矩陣S則調用cov功能函數。在主成分回歸中，主要調用了pca和regress等功能函數。上述計算的數學原理和有關功能函數使用方法參閱相關專著［21-22］。

2　結 果

2.1　多項式肥效模型的多重共線性診斷

根據表2的試驗產量和表1的相關處理施肥量，利用OLS對式（1）進行回歸建模，然后對各個回歸模型進行統計檢驗和模型典型性判別［7］，結果見表3。在7個代表性肥效模型中，1號試驗點未達到統計顯著水平，其余6個試驗點的肥效模型均滿足統計檢驗要求。但是，2號試驗點的P項系數為負數，3號試驗點的推薦施肥量外推，4號試驗點無最高產量點，均屬于非典型式，僅有第5、6、7號三個試驗點的肥效模型滿足了植物營養的一般肥效規律，屬于典型肥效模型。

1號至4號試驗點的OLS回歸建模，出現了未通過顯著性檢驗或者非典型式，是試驗失誤造成的還是回歸方法不合理？為了明確這類問題，對表2的7個試驗資料應用式（2）和式（3）進行多重共線性診斷。以2號試驗點為例，與文獻［4］的表2結果相同，9個回歸變量的方差膨脹因子均遠大于10，平均值達31.90；試驗設計矩陣X的施肥量數據未經標準化處理時，矩陣條件數達7628，即使對各處理施肥量進行標準化轉換，其條件數也達548.8，均顯示肥效模型存在強烈的多重共線性。

進一步對9個回歸變量進行簡單相關性分析，表明N與N2、P與P2、K與K2之間的相關系數高達0.942 9，N與NP或NK之間、P與NP或PK之間、K與NK或PK之間的相關系數達0.738 8，N2與NP或NK之間、P2與NP或PK之間、K2與NK或PK之間的相關系數達0.732 2，存在高度線性相關。因試驗設計方案和肥效模型設定相同，其他6個試驗點的試驗設計矩陣條件數、方差膨脹因子、自變量相關系數等的相關結果與此一致，不再贅述。因此，三元二次多項式肥效模型存在嚴重的多重共線性，且這種共線性主要是由模型設定本身造成的。

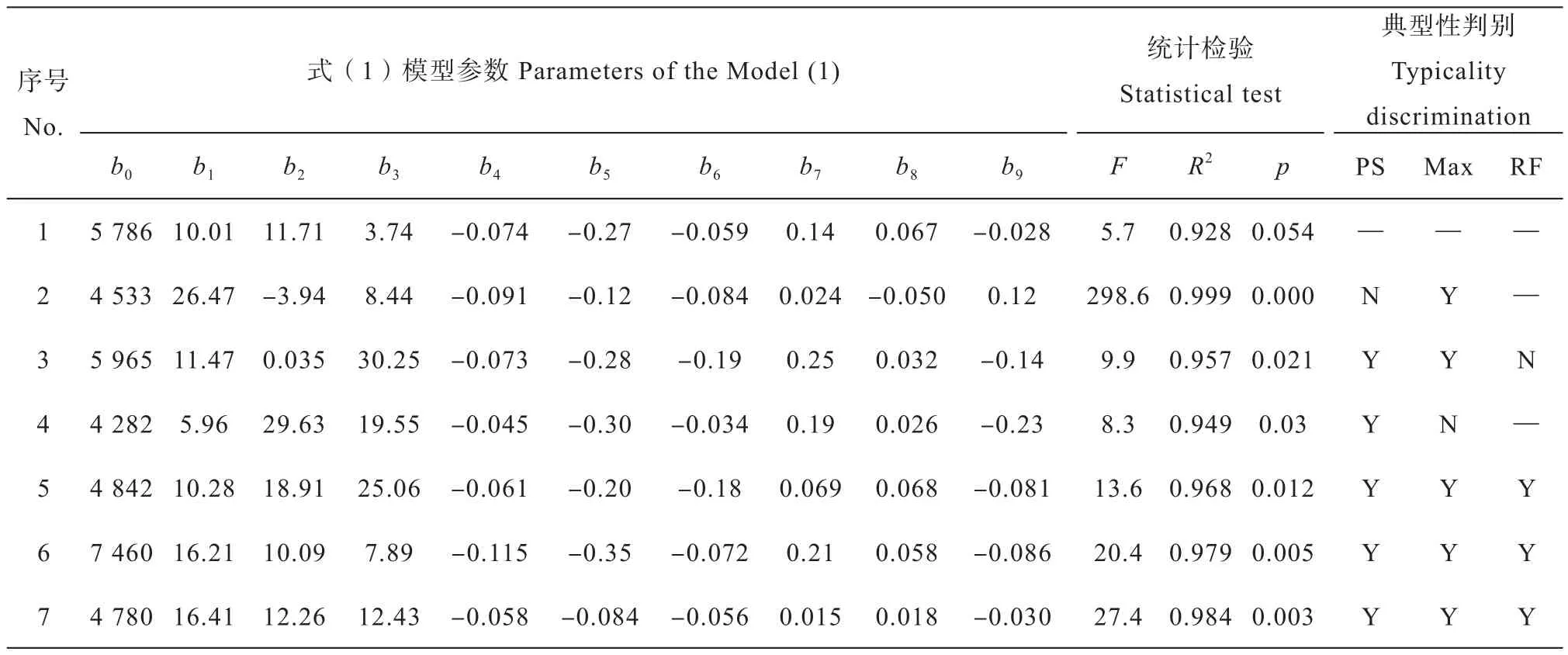
表3　三元二次多項式肥效模型的OLS回歸分析和典型性判別Table 3　OLS regression analysis and typicality discrimination of TQPMs (ternary quadratic polynomial models for fertilizing effect)

2.2　回歸變量的主成分分析及其重構

上述診斷表明，三元二次多項式肥效模型存在嚴重的多重共線性。因此，從重構回歸變量入手來消除這種共線性危害就成為提高建模成功率的關鍵。根據主成分分析原理和式（4），從試驗設計矩陣的原始數據出發，對肥效模型回歸變量進行主成分分析，將式（1）肥效模型的9個回歸變量按照不同的線性組合重新劃分為無線性相關的9個主成分，并與X矩陣特征值對應從大至小排列。同樣以2號試驗點為例，表4的分析表明，具有最大特征值的第1主成分對矩陣X的方差貢獻率達73.82%，前7個主成分累加方差貢獻率達99.9%以上。

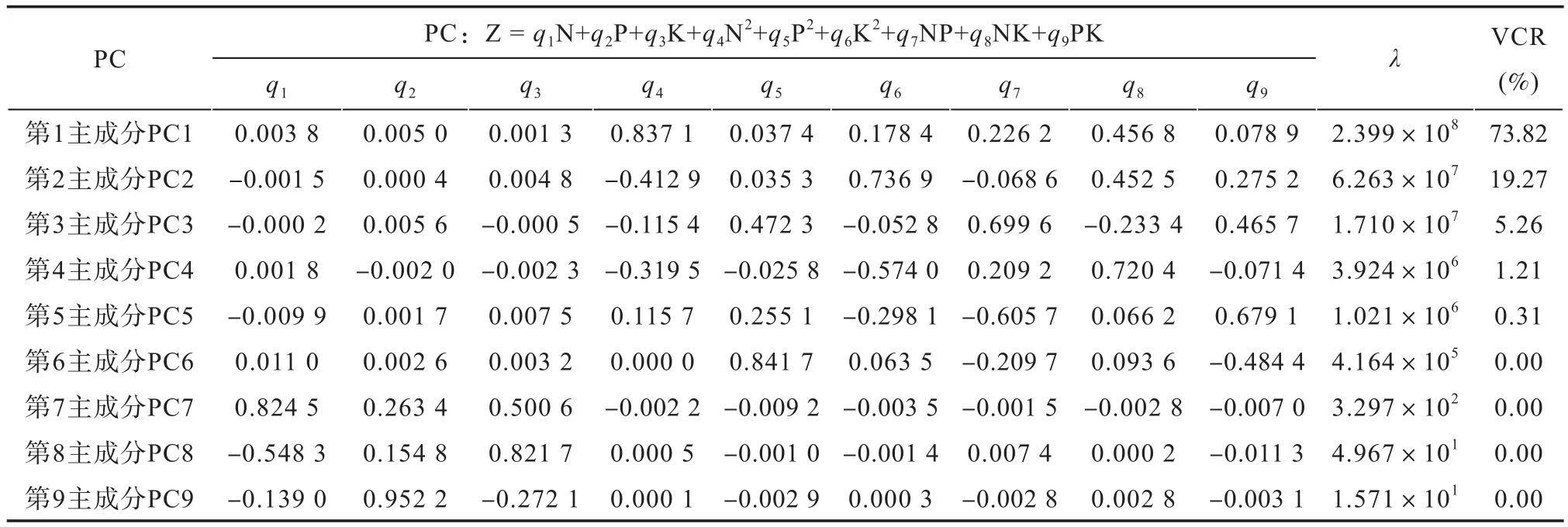
表4　第2號試驗點設計矩陣X的9個主成分及其特征值Table 4 Nine principal components and their eigenvalues of the matrix X designed for Field Trial Site No.2

為了明確9個主成分在反映氮磷鉀施肥效應上的差異，根據式（5）分別計算表4的9個主成分與肥效試驗設計矩陣X的N、P、K、N2、P2、K2、NP、NK、PK等9個回歸變量的決定系數r2（表5）。根據r2值大小結合式（1）肥效模型，第1主成分主要反映了回歸變量N效應，部分反映了NP交互效應；第2主成分主要反映了回歸變量K效應，部分反映了回歸變量N效應；第3主成分主要反映了回歸變量P效應，部分反映了回歸變量N效應；等等。其他試驗點的主成分特點亦有與此類似的結果，不再贅述。

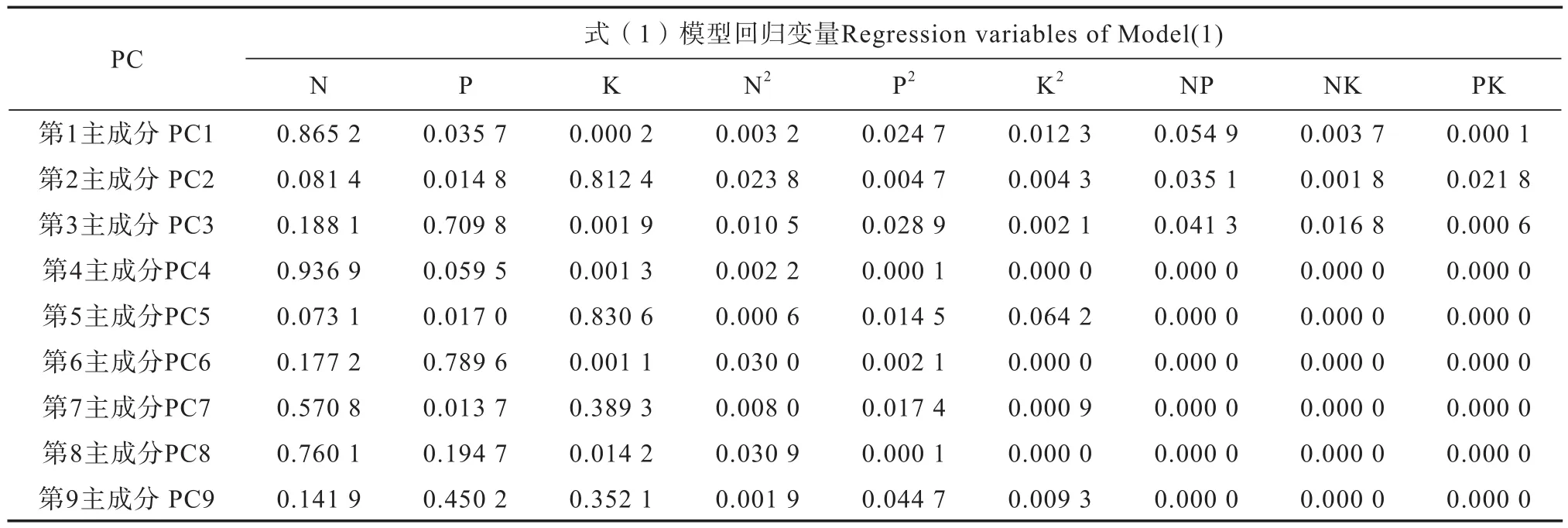
表5 第2號試驗點各回歸變量與9個主成分的決定系數（r2）Table 5　Determination coefficient (r2) between various regression variables and 9 principal componentfor field trial site No.2

2.3　主成分回歸的肥效模型及其推薦施肥量

根據表4各個主成分的N、P、K、N2、P2、K2、NP、NK、PK等回歸變量的線性組合系數和試驗設計矩陣X的每一行對應數值，分別計算14個處理的各自得分值，組成新的設計矩陣。由于前8個或前7個主成分分別反映了X矩陣方差信息的99.99%和99.90%以上，因此，新設計矩陣由前8個主成分或前7個主成分組成。

利用新設計矩陣與對應的14個處理產量，進行OLS回歸并轉化成式（1）函數形式（表6）。由于“3414”試驗的處理數為14個，總自由度為13；采用前8個主成分或前7個主成分進行主成分回歸，就相當于回歸自由度分別為8和7；因而，建立的三元肥效模型的誤差自由度分別為5和6。結果表明，1號、2號和3號試驗點所得三元肥效模型被轉化為滿足植物營養學一般肥效規律的典型式；4號試驗點采用8個主成分進行回歸分析時，其結果與OLS回歸相同均屬于無最高產量點的非典型式，但采用7個主成分回歸即可得到三元典型肥效模型。5號和6號試驗點的OLS回歸分析得到典型式，采用前8個或前7個主成分進行回歸分析仍然得到典型式。但是，7號試驗點采用前8個或前7個主成分回歸，肥效模型均由OLS的典型式變成了非典型式，結果反而變劣。

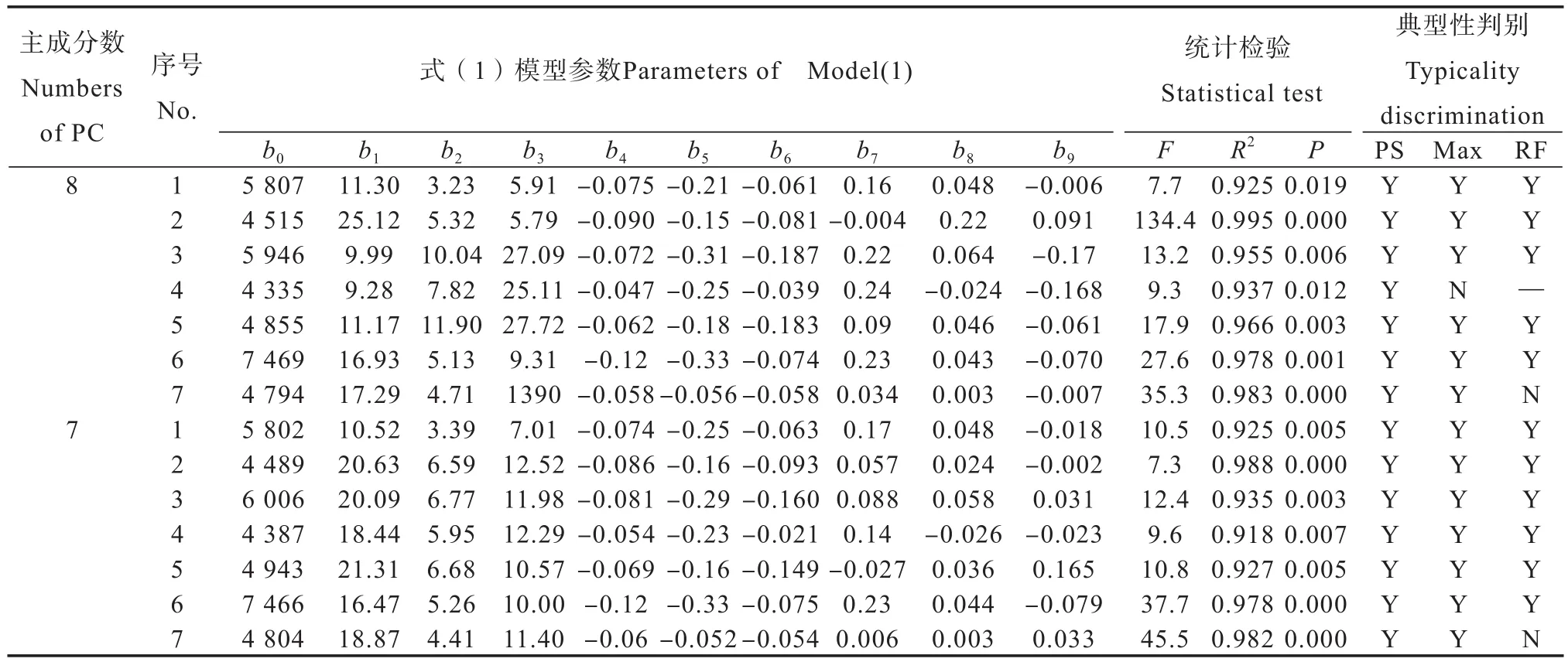
表6 三元二次多項式肥效模型的主成分回歸和典型性判別Table 6　Principal component regression and typicality discrimination of TQPMs

根據主成分回歸建立的典型肥效模型以及每千克 N4.30元、P2O55元、K2O6.0元和稻谷2.0元的市場均價，用邊際產量導數法計算推薦施肥量（表7）。由于選用的前7個或前8個主成分綜合反映了試驗設計矩陣X的99.9%以上的變異方差，1號至4號試驗點主成分回歸模型的最高施肥量和經濟施肥量及其預測產量，其數值大小均在試驗設計施肥量和試驗所得產量范圍內，且與已有的研究結果［17］基本一致。尤其是5號和6號試驗點，主成分回歸的模型推薦施肥量與OLS回歸的模型推薦施肥量差異極小甚至相同，預測早稻產量也基本一致，表明主成分回歸的推薦施肥是可靠的。

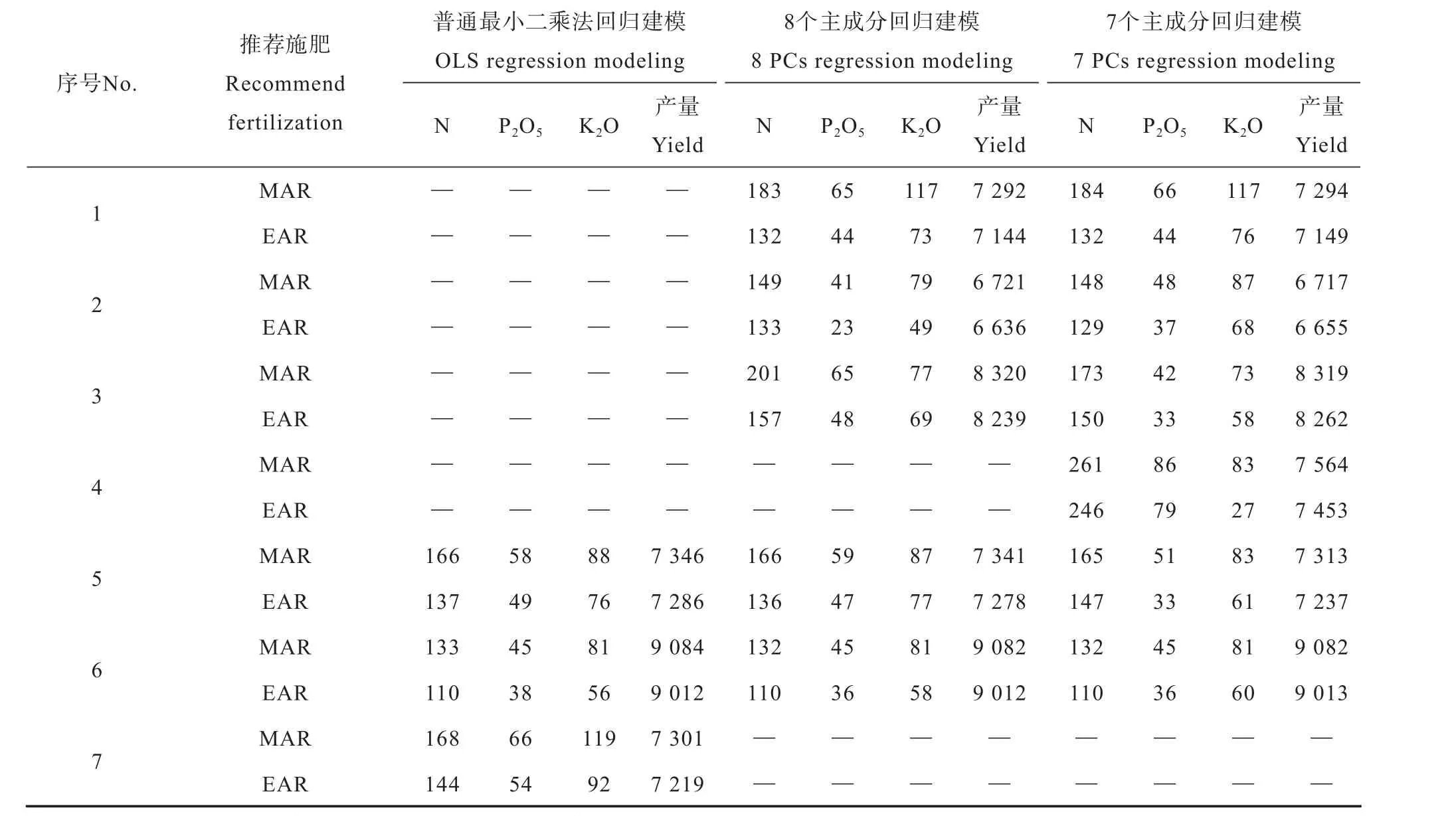
表7　三元二次多項式肥效模型不同建模方法的推薦施肥量比較Table 7　Comparison in recommended application rate between TQPMs different in modeling method

2.4　主成分回歸對三元肥效模型的建模效果

表6的代表性例子表明，主成分回歸能使某些肥效試驗結果由OLS法的未通過顯著性檢驗或非典型式轉化為典型肥效模型，但也可能使OLS法的典型式變成非典型式。為了評價主成分回歸對三元肥效模型的建模效果，利用近年來福建省早稻測土配方施肥工作在主要項目縣完成的 “3414”設計的氮磷鉀田間肥效試驗資料，逐個進行回歸分析和比較，統計結果見表8。

在171個肥效試驗中，OLS回歸建模的三元典型肥效模型的比例占試驗點總數的27.5%，而采用前8個主成分或前7個主成分回歸建模，典型肥效模型的比例則分別提高至41.5%和43.3%，為OLS法的1.5倍和1.6倍。其中，主成分回歸大幅度降低了模型系數符號不合理的非典型式，從OLS法的14.6%下降至幾乎為零；模型無最高產量點的非典型式也從OLS法的36.8%分別下降至32.2%和21.1%。但是，主成分回歸并非利用設計矩陣X的100%方差信息，其建模結果使推薦施肥量外推的非典型式個數反而有所增加。

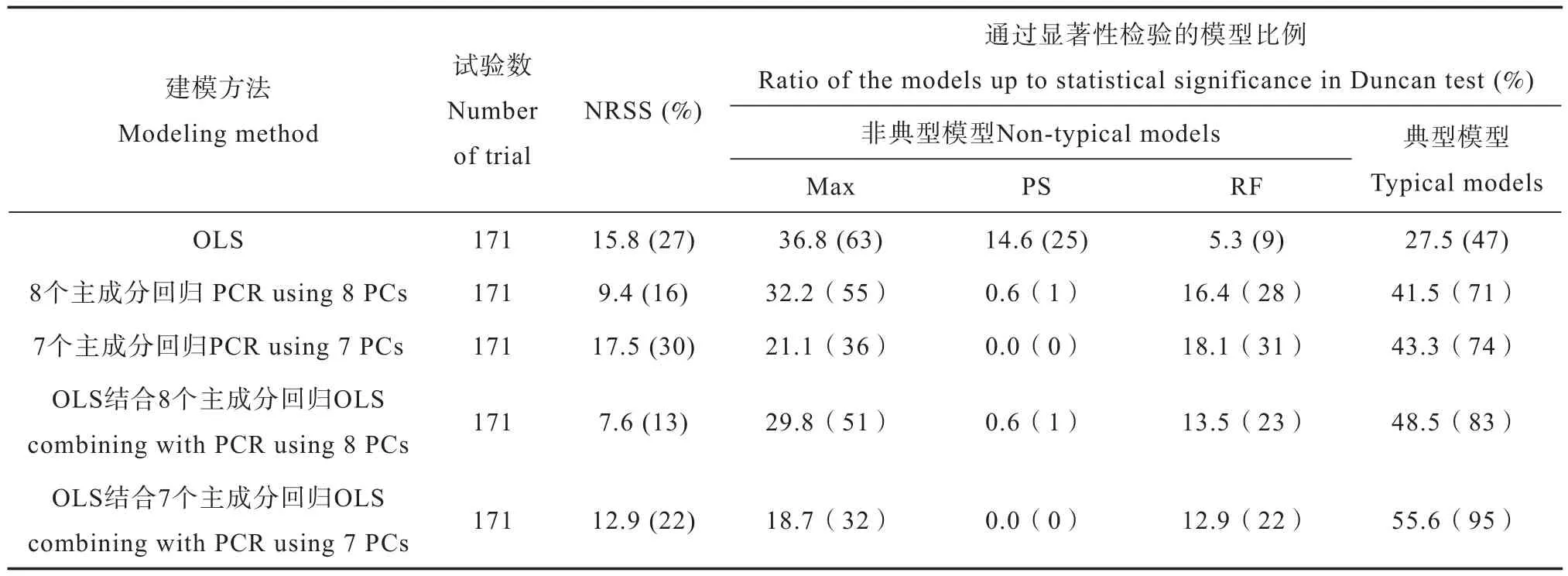
表8　最小二乘法回歸（OLS）和主成分回歸（PCR）對三元二次多項式肥效模型建模結果的影響Table 8　Effects of modeling using OLS and PCR on TQPMs

建模過程還表明，如同7號試驗點，主成分回歸有時也會失效，使OLS法的典型式變為非典型式，甚至造成模型未能通過顯著性檢驗。因此，從實用角度出發，如果主成分回歸僅針對OLS法的非典型式和統計不顯著的肥效模型，即：OLS結合前8個主成分的主成分回歸或者前7個主成分的主成分回歸的建模策略，結果使典型肥效模型的比例分別可提高至48.5%和55.6%，明顯優于單獨使用OLS或者主成分回歸。

3　討 論

3.1　非典型肥效模型的產生原因及其多重共線性危害

經典線性回歸分析理論假設回歸模型的各個自變量之間無多重共線性［19-20］。二次多項式肥效模型在數學形式上是一種非線性模型，人們通常不重視這種模型是否違背了無多重共線性的假設。故這種模型中是否存在共線性、共線性將產生什么危害、如何處理共線性等方面問題，均鮮見相關研究報道［4］。本研究通過方陣XTX條件數和方差膨脹因子［20］等常用指標進行多重共線性診斷，表明這種模型存在嚴重的多重共線性問題。

王興仁［5-6］和章明清等［7］曾報道，二元二次多項式肥效模型的典型式比例僅占40.2%，三元肥效模型的典型式則低至23.6%。人們對多元肥效模型出現大量非典型式的現象至今仍然困惑不解，許多人由此直接歸因于田間試驗失敗或者對肥效模型的應用價值失去信心。研究表明，多重共線性給多項式肥效模型的OLS回歸建模和推薦施肥準確性帶來嚴重危害，具體表現在：①在完全共線性下方陣XTX不可逆，正則方程無解，無法建立肥效模型。②在近似共線性下，雖然可以得到OLS參數估計量，但此時lXTXl ≈ 0，引起方陣XTX主對角線上的元素顯著增大，從而使參數估計值的方差膨脹，難以得到精確的參數估計值，例如3號和4號試驗點出現了非典型肥效模型。③如果模型中兩個回歸變量具有高度線性相關性，那么它們中的一個變量可以由另一個變量近似表征，這時回歸變量前的參數并不反映各自與作物產量之間的結構關系，僅能反映它們對產量的共同影響，結果使參數失去了應有的肥效含義。同時，回歸系數可能變得對產量數據的微小變化異常敏感，甚至越過零值，表現出系數值的正負號出現反常現象，導致參數估計值的專業含義不合理，例如2號試驗點的P項本應為正數，結果卻為負數。④由于方差膨脹，模型顯著性檢驗失效，例如1號試驗點出現未通過顯著性檢驗的假象。⑤膨脹的方差使產量預測區間過度變大，模型的預測功能失效。

因此，現在基本可以明確，非典型肥效模型大多是由多重共線性引起的，肥效模型設定本身是產生多重共線性的主要原因。

3.2　三元二次多項式肥效模型的主成分回歸

多項式統計模型在農學學科中出現大量非典型式的現象，在其他學科諸如經濟學、社會學、心理學等學科也同樣大量存在。主成分回歸經過近幾十年的發展，已成為這些學科對付多重共線性的有效技術［24］。主成分回歸的基本思路是利用主成分分析提取X矩陣的主成分，然后選取方差貢獻率達到符合要求的幾個主成分，計算各處理對應回歸變量的得分值，組成新的設計矩陣，最后利用新設計矩陣與各處理的試驗產量進行OLS回歸建模。本研究表明，這種建模方法能使1號至4號試驗點由OLS法未達統計顯著水平或非典型式轉化為典型式。

在近年來的測土配方施肥工作中，福建省在早稻上完成了眾多“3414”設計的田間肥效試驗。本研究收集整理了來自土肥技術力量較強的主要項目縣完成的171個試驗資料。針對這些試驗結果，選用前8個主成分或前7個主成分進行回歸建模，三元典型式出現比例分別提高至41.5%和43.3%。尤其是前7個主成分回歸建模使模型系數符號不合理的非典型式出現比例下降至零，同時大幅度降低了無最高產量點的非典型式比例（表8），表明了主成分回歸技術在提高三元肥效模型建模成功率方面具有重要的應用價值。

對比研究表明，因各施肥處理的氮磷鉀施肥量所采用的量綱相同，數據差異不顯著，試驗設計矩陣的原始數據是否進行了標準化處理，對主成分回歸結果基本無影響；若將全部9個主成分均納入主成分回歸，其結果與OLS法完全一致，達不到改善建模效果的作用；雖然前5個主成分就能反映X矩陣方差變異的99.87%，但采用6個或者少于6個主成分進行回歸分析，所建立的171個早稻三元二次多項式肥效模型均未能通過顯著性檢驗。因此，對三元肥效模型而言，主成分回歸只能選取前8個主成分或者前7個主成分。

在消除或緩解多重共線性危害方面，數理統計學家已經提出了諸多解決方法［19-20，24］，諸如剔除不重要自變量、擴大樣品容量，或者采用嶺回歸、主成分分析和偏最小二乘法等有偏估計方法來提高參數估計的穩健性。顯然，剔除不重要自變量和擴大樣品容量的方法不適合肥效模型的構建。在有偏估計方法中，嶺回歸估計的質量取決于偏倚系數的選取，但目前尚無標準的決策準則［24］，僅能憑經驗判斷。偏最小二乘回歸是通過迭代算法在X矩陣中逐步提取主成分，使其盡可能多地反映X矩陣的變異方差，同時又兼顧對因變量（產量）的解釋能力。然而，其迭代算法復雜，不易使用。相比而言，主成分回歸具有扎實的統計學基礎，建模思路簡潔明了。該法在目前已有MATLAB、SAS和Stata等諸多成熟軟件可供使用，是較簡便和實用的肥效模型參數估計方法，易于被廣大應用人員理解和掌握。

3.3　三元二次多項式肥效模型的建模策略

盡管主成分回歸具有許多優點，但它畢竟是一種有偏估計。受回歸偏倚的影響，有時會將諸如7號試驗點的OLS回歸典型式變成了非典型式。該法在提取主成分時僅考慮了試驗設計矩陣，而不考慮各個主成分與各處理產量的相關性，而且，對什么樣的試驗數據會造成主成分回歸失效？目前在統計學上并無明確的答案［24-25］。鑒于此，從實用角度出發，主成分回歸僅針對OLS法未通過顯著性檢驗肥效模型和非典型式肥效模型，而對OLS回歸得到典型式的肥效模型就不再做主成分回歸。這個策略使三元典型式的比例進一步提高至55.6%（表8），為單獨使用OLS法的2.0倍。

4　結 論

對三元肥效模型而言，主成分回歸是解決多項式肥效模型多重共線性危害的一種有效方法，OLS建模法結合前7個主成分的主成分回歸是三元二次多項式肥效模型的最佳建模策略。

［ 1 ］ Valkama E，Uusitalo R，Turtola E. Yield response models to phosphorus application：A research synthesis of Finnish field trials to optimize fertilizer P use of cereals. Nutrient Cycling in Agroecosystems，2011，91（1）：1—15

［ 2 ］ Gregoret M C，Zorita M D，Dardanelli J，et al.Regional model for nitrogen fertilization of site—specific rainfed corn in haplustolls of the central Pampas，Argentina. Precision Agriculture，2011，12（6）：831—849

［ 3 ］ 王興仁，陳新平，張福鎖，等. 施肥模型在我國推薦施肥中的應用. 植物營養與肥料學報，1998，4（1）：67—74 Wang X R，Chen X P，Zhang F S，et al. Application of fertilization model for fertilizer recommendation in China（In Chinese）. Plant Nutrition and Fertilizer Science，1998，4（1）：67—74

［ 4 ］ 章明清，李娟，孔慶波，等. 作物肥料效應函數模型研究進展與展望. 土壤學報，2016，53（6）：1143—1156 Zhang M Q，Li J，Kong Q B， et al. Progress and prospect of the study on crop—response—to —fertilization function model（In Chinese）. Acta Pedologica Sinica，2016，53（6）：1143—1156

［ 5 ］ 王興仁. 二元二次肥料效應曲面等產線圖在科學施肥中的位置（一）. 土壤通報，1985，16（1）：30—34 Wan X R. The positions of contour map of yield of binary quadratic fertilizer response curve in scientific fertilization（part 1）（In Chinese）. Chinese Journa1 of Soil Science，1985，16（1）：30—34

［ 6 ］ 王興仁. 二元二次肥料效應曲面等產線圖在科學施肥中的位置（二）. 土壤通報，1985，16（2）：86—88 Wan X R. The positions of contour map of yield of binary quadratic fertilizer response curve in scientific fertilization（part 2）（In Chinese）. Chinese Journa1 of Soil Science，1985，16（2）：86—88

［ 7 ］ 章明清，林仁塤，林代炎，等. 極值判別分析在三元肥效模型推薦施肥中的作用. 福建農業學報，1995，10（2）：54—59 Zhang M Q，Lin R X，Lin D Y，et al. Function of distinguish analysis on extreme value in recommendatory fertilization for three—fertilizer efficiency model（In Chinese）. Fujian Journal of Agricultural Sciences，1995，10（2）：54—59

［ 8 ］ Cerrato M E，B1ackmer A M. Comparision of models for describing corn yield response to nitrogen fertilizer.Agronomy Journal，1990，82（1）：138—143

［ 9 ］ 楊靖一，Wadsworth G A，Greenwood D J. 三種蔬菜N肥效應曲線的比較研究. 植物營養與肥料學報，1995，1（1）：71—78 Yang J Y，Wadsworth G A，Greenwood D J.Comparative study on three kinds of vegetables response to N fertilizer curve（In Chinese）. Plant Nutrition and Fertilizer Science，1995，1（1）：71—78

［10］ 陳新平，周金池，王興仁，等. 小麥—玉米輪作制中氮肥效應模型的選擇——經濟和環境效益分析. 土壤學報，2000，37（3）：346—354 Chen X P，Zhou J C，Wang X R，et al. Economic and environmental evaluation on models for describing crop yield response to nitrogen fertilizers at winter—wheat and summer—corn rotation system（In Chinese）. Acta Pedologica Sinica，2000，37（3）：346—354

［11］ 吳平，陶勤南. 氮磷鉀肥效模型的研究及其應用. 浙江農業大學學報，1989，15（4）：383—388 Wu P，Tao Q N. Study on N，P and K fertilizer response model and its application（In Chinese）.Journal of Zhejiang Agricultural University，1989，15（4）：383—388

［12］ 章明清. 米氏肥效方程的灰色建模法. 土壤通報，1997，28（1）：18—19 Z h a n g M Q. G r a y m o d e l i n g m e t h o d o f Mitsherlich fertilizer response equations（In Chinese）. Chinese Journa1 of Soil Science，1997，28（1）：18—19

［13］ 章明清，徐志平，姚寶全，等. Monte Carlo 法在多元肥效模型參數估計和推薦施肥中的應用. 植物營養與肥料學報，2009，15（2）：366 —373 Zhang M Q，Xu Z P，Yao B Q，et al. Using Monte Carlo method for parameter estimation and fertilization recommendation of multivariate fertilizer response model（In Chinese）. Plant Nutrition and Fertilizing Science，2009，15（2）：366—373

［14］ C o l w e l l J D. T h e d e r i v a t i o n o f f e r t i l i z e r recommendations for crops in non—uniform environment：Fertilizer. Crop Quality and Economy，1974：936—961

［15］ 王興仁，陳倫壽，毛達如，等. 分類回歸綜合法及其在區域施肥決策中的應用. 土壤通報，1989，20（1）：17—21 Wang X R，Chen L S，Mao D R，et al. Classification of regression synthesis and its application for regional fertilization decision—making（In Chinese）. Chinese Journa1 of Soil Science，1989，20（1）：17—21

［16］ 毛達如，張承東. 多點肥料效應函數的動態聚類方法.北京農業大學學報，1991，17（2）：49—54 Mao D R，Zhang C D. Cluster analysis of quadratic response function on the fertilizer dispersed experiment（In Chinese）. Acta Agriculturae Universitatis Pekinensis，1991，17（2）：49—54

［17］ 李娟，章明清，孔慶波，等. 福建早稻測土配方施肥指標體系研究. 植物營養與肥料學報，2010，16（4）：938—946 Li J，Zhang M Q，Kong Q B，et al. Soil testing and formula fertilization index for early rice in Fujian Province（In Chinese）. Plant Nutrition and Fertilizer Science，2010，16（4）：938— 946

［18］ 魯如坤．土壤農業化學分析方法．北京：中國農業科學技術出版社，2000：146—196 Lu R K. Analytical methods for soil and agro—chemistry（In Chinese）. Beijing：China Agricultural Science and Technology Press，2000：146—196

［19］ 何曉群，劉文卿. 應用回歸分析. 第3版. 北京：中國人民大學出版社，2013：158—170 He X Q，Liu W Q. Applied regression analysis（In Chinese）. 3rd ed. Beijing：China Renmin University Press，2013：158—170

［20］ Montgomery D C，Peck E A，Vining G G. 王辰勇，譯. 線性回歸分析導論. 第5版. 北京：機械工業出版社，2016：91—268 Montgomery D C，Peck E A，Vining G G. Wang C Y. trans. Introduction to linear regression analysis（In Chinese）. 5th ed. Beijing：China Machine Press，2016：91—268

［21］ 袁志發，宋世德. 多元統計分析. 第2版. 北京：科學出版社，2009：219—250 Yuan Z F，Song S D. Multivariate statistical analysis（In Chinese）. 2nd ed. Beijing：Science Press，2009：219—250

［22］ 薛毅，陳立萍. 實用數據分析與MATLAB軟件. 北京：北京工業大學出版社，2015：189—274，377—394 Xue Y，Chen L P. Practical data analysis and MATLAB software（In Chinese）. Beijing：Beijing University of Technology Press，2015：189—274，377—394

［23］ Gujarati D N，Porter D C，費劍平，譯. 計量經濟學基礎（上冊）. 第5版. 北京：中國人民大學出版社，2011：313—399 Gujarati D N，Porter D C. Fei J P. trans. Econometrics foundation（the first volume）（In Chinese）. 5th ed. Beijing：China Renmin University Press，2011：313—399

［24］ 王惠文，王劫，黃海軍. 主成分回歸的建模策略研究.北京航空航天大學學報，2008，34（6）：661—664 Wang H W，Wang J，Huang H J. Modeling strategy of principle component regression（In Chinese）.Journal of Beijing University of Aeronautics and Astronautics，2008，34（6）：661—664

［25］ 葉宗裕. 主成分回歸能消除多重共線性嗎? 統計與信息論壇，2012，27（3）：15—20 Ye Z Y. Can the principal components regression eliminate the malticollinearity（In Chinese）?Statistics & Information Forum，2012，27（3）：15—20