淺談類比推理在小學數學中的運用
羅 蛟
(樂山市海棠實驗中學 四川樂山 614000)
引言
類比推理,簡單的說,就是對兩個相同或相似的思維對象進行比較,從而推出它們更多相同或相似的地方,是一種生動、活波、自由的數學思維方法。《小學數學新課程標準(2011年修訂版)》在“總體目標”中明確提出:讓學生學會獨立思考,體會數學的基本思想和思維方式。這對數學思維方法在小學數學教學中的滲透提出了新的要求。類比推理作為一種生動、活波、自由的數學思維方法,在數學的學習中來認識和學習類比推理是比較簡潔、明了,易于表達和訓練的,是符合小學生心理和認知發展特點的。整個小學數學教材貫穿著兩條線,一條是數學知識(明線),另一條是數學思維(暗線),前者可以看作是戰術性線,后者可以看作是戰略性線,圍繞戰略性線進行教學,才是數學教學取得成功的基本保證。有了數學思維,數學知識就不再成為零散的東西,數學方法也就不再是死板的教條,從而能從整體上把握數學教學,因此,加強數學思維方法的研究,是數學教學的新視角,在教學中需要教師不斷的去挖掘和滲透。本文通過一些教學中的實例,探討類比推理在小學數學教學中的具體應用。[1]
一、在解方程中的運用
學生在解這個方程過程中不知道如何移項,符號該如何確定,老師在黑板上講解完后,下次做這這樣的題,學生照樣出錯,因為他們根本沒有從本質上掌握這個題的思想方法。此時我們運用類比推理的方法給學生作講解:[2]
如:6÷2=3這個式子大家都能理解

通過類比我們可以非常容易清晰的理解這個方程的解法,學生理解更加清晰,思維方法更容易掌握。
二、分數乘除法應用題中的運用
這是一道分數乘除法的題,從題意來說兩個分數,很多學生理解起來較困難,下面我們用類比的方法來解決這道題。
如:小明2分鐘吃3個蘋果,那么6分鐘能吃幾個蘋果?吃12個蘋果要用多少時間?
學生很容易理解6分鐘里面有6÷2=3個2分鐘,所以應該吃了3×3=9個蘋果
1.個蘋果里面有12÷3=4個2分鐘,所以應該要用4×2=8分鐘。
通過類比推理給學生講解此題,從整數過度到分數,理解更加容易多了。
三、在“比的意義”的教學中的應用
在教學“比的意義”時,學生剛開始接觸一個新的概念,理解比較困難,但學生對已經學過的除法和分數的性質非常熟悉,我們可以通過對除法和分數的性質進行復習,讓學生自己去類比除法、分數和比,觀察探索發現它們之間的關系:

?
引導學生根據分數和除法來理解比的意義,搞清它們之間的聯系和區別。這樣的講授使新知識更加簡單通俗易懂,學生容易理解容易掌握。由此可見學生在學習新知識時,如果老師能夠合理的引導學生對新舊知識進行類比學習,這樣能讓學生學的更加輕松愉快,讓課堂更加開放、靈活。
四、在“比的基本性質”教學中的應用
學生通過類比理解了比的意義,我們可以通過讓學生進行類比觀察找規律,繼續自己總結結論,這樣理解更加透徹。
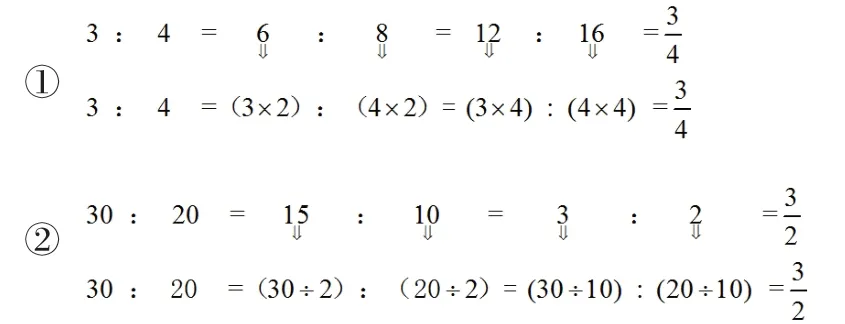
讓學生通過第一組數據和第二組數據類比觀察發現規律:比的前項和后項同時乘或除以相同的數,比值不變。類比分數的分母不能為0,除法中的除數不能為0,得出比的前項和后項除以的數不能為0。
結語
總之,類比推理作為小學數學教學中比較常用的一種思維方法,不但可以讓學生在觀察發現中理解一些抽象的數學問題,而且可以激發學生的求知欲,提高學生的思維分析能力和探究創新能力,促進學生更好的理解和掌握新知識,讓學生體會到發現的快樂和成功的喜悅,提高學習效率。

