化歸方法及其應用

計 軍

（遼寧省彰武縣滿堂紅九年制學校 遼寧阜新 123200）

數學在其漫長的發展過程中，不僅構建了嚴密的思想體系，而且形成了一套行之有效的思想方法，劃歸思想就是常用的方法之一。

一、化歸原則

人們在研究和運用數學的長期實踐中，獲得了大量的成果，也積累了豐富的經驗，許多問題的解決也形成了固定的方法模式和約定俗成的步驟。人們把這種有既定解決方法和程序的問題叫做規范化或稱為化歸，化歸就是運用某種方法和手段把有待解決的較為生疏較為復雜問題歸結為所熟悉的規范性問題來解決的方法。[1]

例如，對于一元二次方程，人們已經掌握了求根公式，因而求解一元二次方程的問題是規范問題，而把分式方程、無理方程通過換元等方法轉化為一元二次方程就是問題的規范化。其中換元是實現規范化的手段，具有轉化歸結的作用，可以稱這為化歸的方法。

規范問題具有確定性，相對性和發展性的特征。對于規范問題，人們不但可以運用書籍的理論和技術達成問題的解決，而且已經掌握了固定的步驟和程序，這就是確定性，所謂相對性，是指對于數學研究工作者以及不同層次的學習者，規范問題的范圍并不相同。例如建于高中生和初中生而言，對于初中生不是規范性問題對于高中生就可以看作規范性問題，隨著個人數學知識的增長，規范問題也在不斷擴大，因此規范問題又具有發展性。[2]

化歸原則的核心是實現問題的規范化。也就是把一個生疏的、復雜的問題化為熟悉的、簡單的問題，以便利用已知的理論、方法和程序實現問題的解決，它的結構圖如下所示。由此不難看出，熟悉化和簡單化是化歸的基本方向。

二、化歸原則的基本思想

化歸原則的結構中蘊涵著三個基本要素，即化歸的對象，目標和方法，化歸的對象就上待解問題中需要變更的成分，化規的目標是指所要達到的規范問題。所謂化歸的方法，就是規范化的手段，措施和技術。例如對于初中生而言解二元一次方程組，一般要化為一元一次方程，這里二元一次方程線是化歸對象，一元一次方程是化歸的目標，而把二元一次方程組化為一元一閱人多矣次方程所用帶入法或加減法就是化歸的方法，在化歸的三要素中，化歸應選是實現化歸的關鍵，這是顯而易見的。唯物辯證法指出，客觀事物是發展變化的，不同事物間存在著種種聯系，各種矛盾無不在一定的條件下互相轉化，化歸正式人們對這種聯系和轉化的一種能動的反映。從哲學的高度看，化歸原則著眼于提示矛盾實現轉化，在遷移轉化中達到問題的規范化。因此，化歸原則裨上是轉化矛盾的原則，它的“運動－轉化－解決矛盾”的基本思想具有深刻的辨證性質。

三、化歸原則中，實現化歸的方法是多樣的

按照應用范圍的廣度來劃分，數學中的化歸方法分為三類，就是多維化歸方法，二維化歸方法和單維化歸方法。

1.多維化歸方法，就是跨越多種數學分支，廣泛適用于數學各學科的化歸，歸方法。例如，換元方法，恒等變換法、反證法、構造法、待定系數法、數學歸納法等，它們既適用于幾何、三角等初等數學的各個分支，又適用于高等數學的各個分學科，其應用十分廣泛，因而屬于多維化歸方法。

2.二維化歸方法，這是指溝通兩個不同數學分支學科的化歸方法，是兩個分支學科之間的轉化。例如，解析法、三角帶換法等都可以溝通兩個數學分支學科，以便發揮兩個學科的理論和方法的優勢實現問題的解決，因而都是二維化歸方法。

3.單維化歸方法，這是只適用于某一學科的化歸方法。是本學科系統內部的轉化。例如，代入法、加減法、判斷式法、坐標變換法等都是單維化歸方法。[3]

例1： 如圖，菱形ABCD中，AB=2、∠BAD=60°，E是AB的中點，P是對角線AC上任一動點，則PE+PB的最小值是多少？

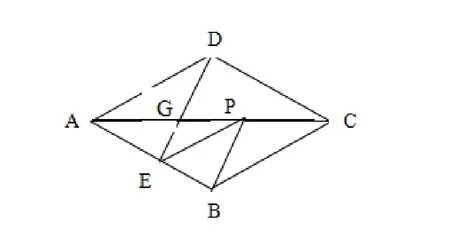
分析：求PE+PB的最小值問題可以轉化為“求作線段AC上一點G，使G到已知點E、B的距離之和最短”的問題，這個簡單問題被放到菱形中去，自然的想到菱形是軸對稱圖形，我們只要連接E和B關于AC的對稱點D，則線段DE與AC的交點G，就是線段AC上到點E、B的距離和最笑的點，由于GB=GD，所以GB+GE=DE在等邊△AB D中，易求出DE=，故PE+PB最小值為。

例2：解方程組 2X－Y＋Z=－1 ①

X＋3Y－2Z=－5 ②

4X－3Y－5Z=7 ③

分析這是一個三元一次方程組，考慮先化為二元一次方程組，再化為一元一次方程組，具體方法為 ②＋③得5X－7Z=2④

①X3得＋②得7X＋Z=－8⑤

得二元一次方程組 5X－7Z=2 ④

7X＋Z=－8 ⑤

第一次化歸完成，再由⑤得Z=－8－7X代入④

得關于X的一元一次54X=54達到化歸目的。

例3：某工件的形狀如圖所示，圓弧BC的度數為60?，B=6cm，點B到點C的距離等于AB，∠ BAC=30?，則工件的面積等于（）

（A）4π （B）5π （C）8π （D）10π

分析：本題所給的圖形是陌生的，為此我引導學生設法分解圖形，將它轉化為我們熟悉的基本圖形，如連接，即出現一個等腰三角形ABC和一個弓形，對于弓形可進一步補全圖形畫出BC所在的圓，將其轉化為個圓的面積的問題，顯然，其工件面積為6π，選B.