卡爾曼濾波GNSS數據處理模型
——GNSS動態載波相位測量的數據處理方法之二

劉基余，陳小明

（武漢大學測繪學院，武漢 430079）

利用卡爾漫濾波處理GNSS動態測量數據，需要首先建立濾波的動態模型（狀態方程）和觀測模型（觀測方程）。對GNSS動態定位而言，動態模型難以用精確的數學公式來表達，實用中一般在精度損失較小的前提下對動態模型進行簡化。最常用的動態模型為常速模型或常加速模型。常速模型或常加速模型的選擇依賴于運動載體的運動狀態以及數據采樣率的高低，在高精度GNSS動態定位中數據采樣率一般為1秒或更高，此時可采用常速模型。動態噪聲可假定為零均值高斯噪聲。在整周模糊度已知時（利用基線初始化或模糊度在航解算OTF求得），單純利用雙差載波相位觀測量就可以獲得極高的動態定位精度。

由于載波相位測量的整周模糊度特性，在載波相位測量出現周跳后，整周模糊度會發生改變。若不能及時修正，將嚴重影響動態定位的精度。在濾波設計時，需要考慮對周跳的探測與修復。另一個方面要考慮到動態接收機機動情形，在濾波設計時，更需考慮對機動加速度的補償。中國魏明博士等（1990）和盧剛博士等（1991）分別提出了用統計檢驗的方法來探測周跳和機動加速度，并利用兩步卡爾曼濾波來估計周跳的方法；盧剛博士等（1990）稱之為GPS動態定位的統計質量控制（Statistical quantity control）。為了研究質量控制的有效性，本文提出利用可靠性理論來分析周跳探測，機動探測的能力以及周跳與機動加速度的可區分性問題，并在此基礎上提出一種更為簡單實用的高精度GNSS動態定位模型。

1 基本濾波模型及其遞推方程

狀態方程：

觀測方程：

系統動態噪聲和量測噪聲的統計特性假設如下：

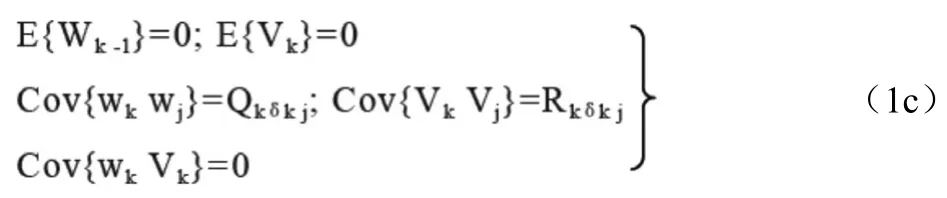
式（1a）中動態模型采用常速模型。狀態轉移矩陣Φk，k-1和干擾矩陣Γk-1定義如下：

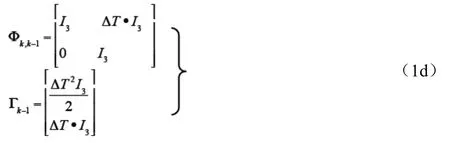
式中，I3為3×3維單位陣；ΔT為采樣時間間隔。

式（1b）為采用雙差載波相位觀測量的觀測方程。雙差載波相位觀測值可選為L1、L2單頻載波相位或雙頻組合觀測值，其頻率為f，波長為λ=C//f。該式為非線性方程。令式（1b）圍繞參考估計（一般選為當前時刻的預報值Xk，K-1）線性化，可得到線性化觀測方程

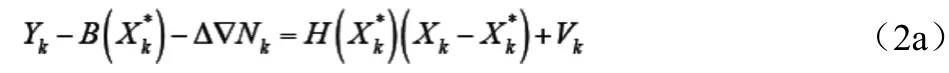
或記為

式中，YK為雙差載波相位觀測向量；為相位的雙差整周模糊度向量。

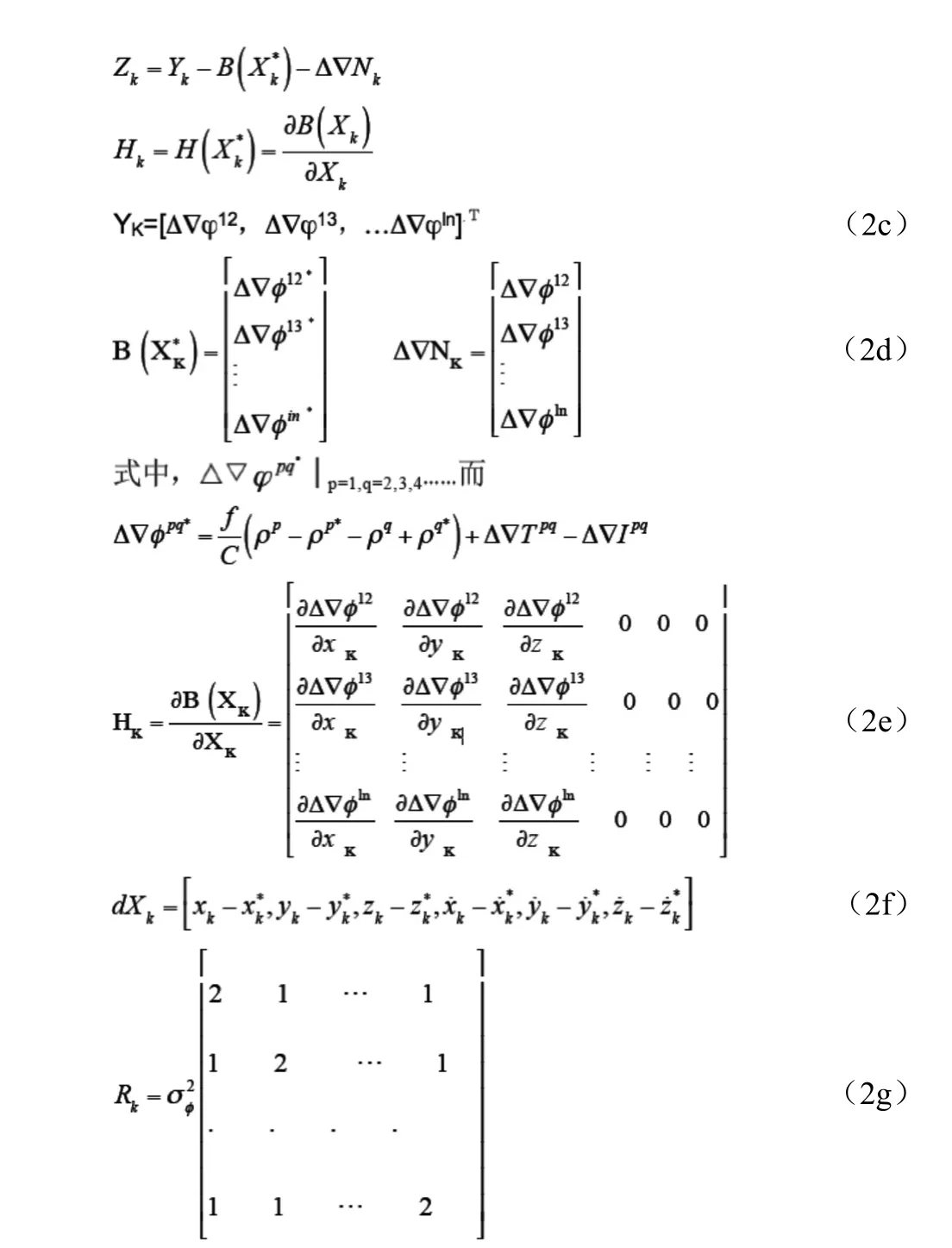
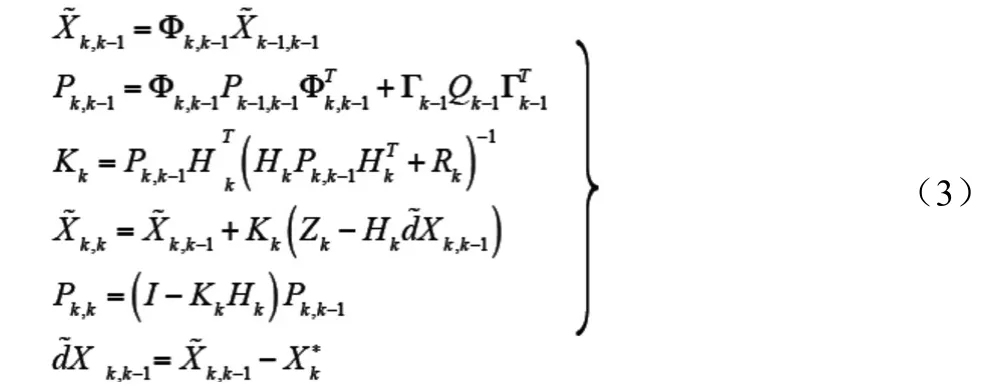
卡爾曼濾波的初值為X0/0，P0/0。

2 GPS動態定位的質量控制

在前述的基本濾波模型中未考慮運動載體的機動以及觀測值中可能存在的粗差（周跳）。由于機動加速度和周跳可以常值為差來模擬，在出現機動或發生周跳時可在濾波狀方程和觀測方程中加入相應的修正量，此時濾波模型為：

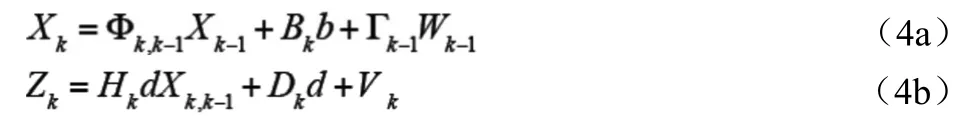
式中，b，d分別表示機動加速度和雙差周跳。當不存在機動加速度時，b=0；當不存在周跳時，d=0；當b，d同時為零時，模型（4a）、（4b）退化為（1a），（2b）。BK，DK分別為機動加速度、雙差周跳對應的系數陣。BK定義如下：

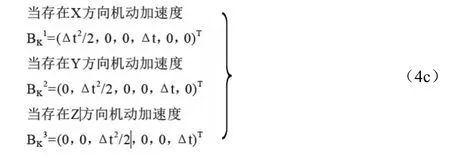
DK定義如下：對應第i個雙差周跳，有

若已知機動加速度b和雙差周跳d，則時刻k動態接收機天線的位置、速度預報值和濾波分別為：

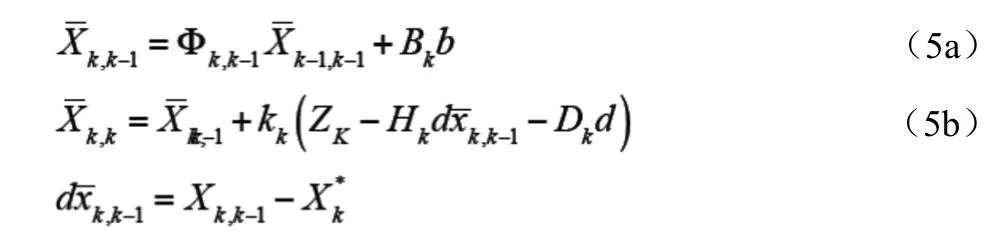
當存在機動加速度和（或）雙差周跳，但仍采用模型式（1a）和式（3b），而利用式（3a）～（3f）進行遞推計算值時，遞推估值，將不是最優無偏估計而是有偏的。當觀測方程是非線性方程時，有偏估計與無偏估計之間的偏差關系也是非線性的。可以證明，當忽略線性化誤差時，無偏估計和有偏估計間的偏差值可用b、d的線性關系式表達。下面進行詳細推導。

設有偏估計和無偏估計差值可用下列線性關系式表達

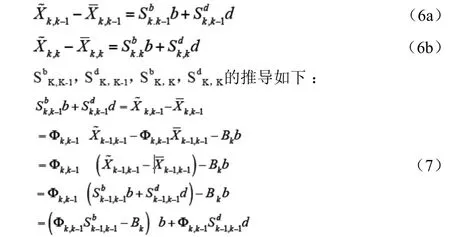
比較式（7）兩端系數，可得到遞推關系

將觀測方程圍繞參考估計線性化，有

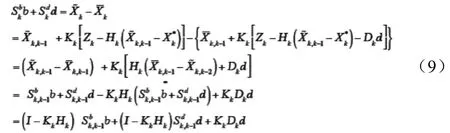
比較式（9）兩端系數可得到

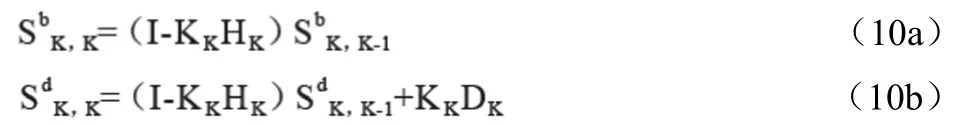
式（8a）、式（10a）、式（8b）和式（10b）分別構成遞推計算公式。在b、d已知時，可將無偏差參數模型式（1a）和式（2b）計算得到的有偏估計修正為最優無偏估計。b、d可由兩步卡爾曼濾波的方法來確定。

關鍵的問題在于如何探測何時出現機動、周跳，以及機動出現在哪個方向上、周跳出現在哪個雙差觀測值上。機動以及周跳的探測可以通過對預報殘差進行統計檢驗來完成。

根據卡爾曼濾波理論，在濾波模型存在偏差或對偏差進行了修正時，預報殘偏差應該是零均值的白噪聲。若實際系統存在偏差，但在濾波模型中未進行修正，則預報殘差將不再是零均值的白噪聲。當存在偏差b、d時，采用濾波模型式（4a）和式（4b）的預報殘差為：

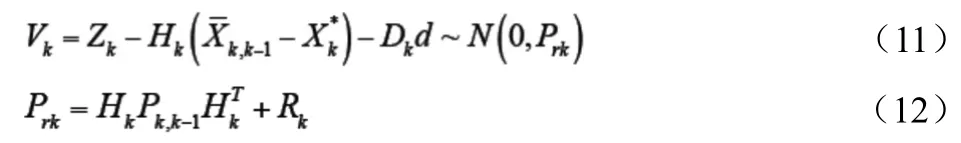
若采用濾波模型式（6a）和式（6b），則預報殘差為：

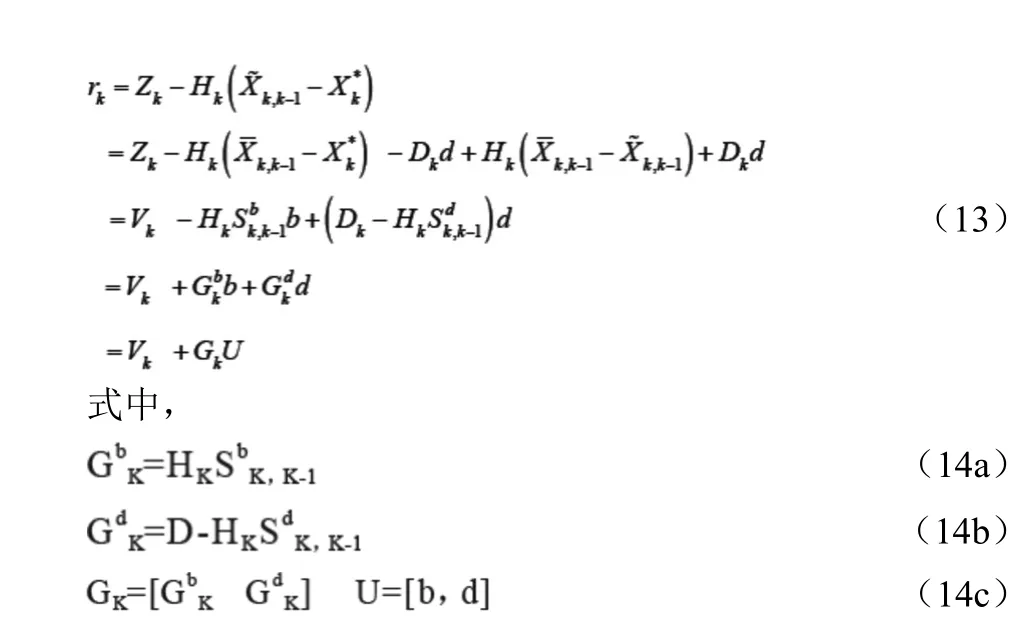
由于b、d是常值偏差，因而rK服從均值為GKU，方差為的正態分布

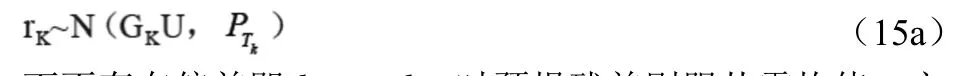
而不存在偏差即b=0，d=0時預報殘差則服從零均值，方差為的正態分布

根據采用無偏差參數模型式（2a）和式（2b）計算得到的新息序列在有、無偏差時的統計特性，可以構造如下原假設H0和備選假設Ha：

上述檢驗可構造如下統計檢驗量

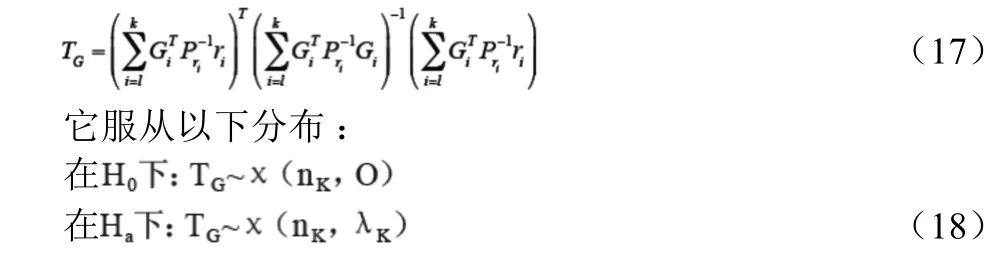
式中，nK為偏差向量U的維數；λK為非中心化參數，定義為

上式所構成的偏差統計量可分為兩種情況；當l=k時，僅利用當前觀測時元的預報殘差構成統計量，稱為局部模型檢驗 LMT（Local Model Test）；

當K＞l時，則利用多個時元的預報殘差構成統計量，稱為全局模型檢驗GMT（Global Model Test）。全局模型檢驗探測系統模型偏差的能力比局部檢驗強，但存在檢驗延遲的問題，且計算量比局部檢驗大。

根據假設檢驗理論，選定所需檢測的偏差，構造相應系數陣GK并選定某一顯著性水平a，并取F=（nk）可以得出如下判斷標準：當TG＜F時，接受原假設H0；當TG≥F時，接受備選假設Ha。

從理論上講，這種檢驗方法是成立的。但從實際應用來看，此方法很難實行，因為在濾波計算時我們并不知道哪個方向發生機動或哪個觀測值有周跳。因此，實用中常采用以下方法。

首先選取偏差向量的維數等于預報殘差的維數，此時Gi陣為可逆方陣，此時統計量TG變為如下形式

在H0下有

式中，mi為第i個觀測時元預報殘差的維數。上式實際上只是一個預警檢驗統計量，它僅能用于判斷系統是否出現故障。當k=l時，即僅利用當前觀測的預報殘差，稱為局部預警檢驗。此時在H0下有

選擇一顯著性水平a，并取接受H0，即認為既無機動也無周跳，當≥F1時，接受Ha，即認為可能存在機動或周跳。此時應對故障原因進行進一步診斷，從而對偏差源進行定位。中國魏明博士和盧剛博士建議采用類似巴爾達的數據探測（Data Snooping）的方法進行，即對每假定的偏差源分別采用一維的檢驗一統計量進行定位檢驗，直到檢測出全部可能的偏差。

當檢測機動加速度時，則有

或者寫成

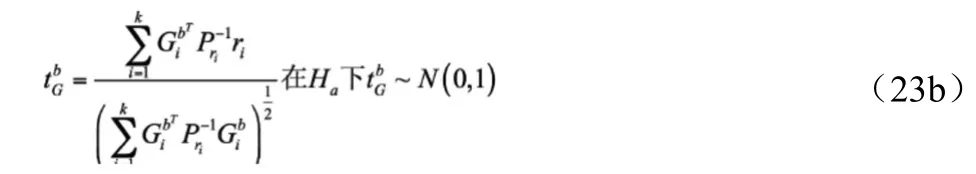
式（23a）和式（23b）為檢驗機動加速度的全局一維定位檢驗量，若令k=1，則形成局部一維定位檢驗量，此時有

式（24a）和（24b）為檢驗周跳的全局一維定位檢驗量，若令k=1則形式相應的局部一維定位檢驗量，此時有

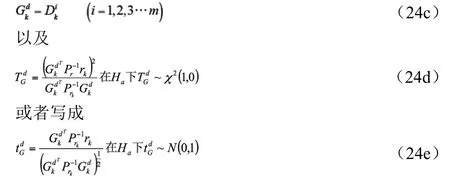
盧剛博士（1991）認為局部預警檢驗和局部定位檢驗對GPS相對定位中觀測值進行偏差的檢驗和定位已足夠，因為最常見的偏差如周跳等均影響當前時刻的濾波值。

在實用中，我們發現上述局部統計量對周跳很敏感而對機動加速度則不甚敏感，往往在機動發生若干時元之后才能探測到。另外，當QK選擇大于某一數值時，或者選得更大，即使不對機動加速度引起的濾波估計偏差進行補償也能獲得很好的濾波結果。下面我們用可靠性理論對上述現象進行研究分析。

3 可靠性分析

可靠性研究建立在數理統計假設檢驗的基礎上。經典的假設檢驗理論是1955年由萊曼和皮爾孫提出的。在測量平范疇內，可靠性研究理論是由荷蘭巴爾達教授在1967～1968年提出的。巴爾達的可靠性理論是從單個一維備選假設出發，研究平差系統發現單個模型誤差的能力和不可發現的模型誤差對平差結果的影響。前者稱為內部可靠性，后者稱為外部可靠性。這里的模型誤差包括粗差和系統誤差。此外，從已知單位權方差出發，巴爾達教授還導出了檢驗粗差的數據探測法（Data Snooping），即以服從正態分布的標準化殘差作為統計量。

隨后，由Fotstner和Koch等人將該理論推廣到單個多維備選假設，從而研究系統發現多個模型誤差的能力。1983年Fotstner第一次提出了模型誤差的區分可能性，并從兩個一維備選假設出發，導出了區分可能性本質上取決于檢驗量之間相關系數的結論。李德仁院士在他的博士論文中從高斯-馬爾可夫模型含兩個多維備選假設出發，提出了平差系統的可區分性和可靠性理論。該理論可研究全系統發現并區分不同模型誤差的區分和定位提供了研究的基本理論和定量的尺度。

近年來，可靠性研究理論已在大地測量、攝影測量、工程測量及形變測量中取得了廣泛的應用。這一理論也已被引入到集成導航系統的設計之中。下面應用可靠性理論來研究卡爾曼濾波處理高精度GPS動態定位數據的內外部可靠性。

3.1 內部可靠性分析

在單個備選假設下，內部可靠性研究的是若檢驗以一定的顯著水平進行時能以什么樣的把握（檢驗功效βP）發現模型誤差。在多數情況下，由于模型誤差的大小是未知的，內部可靠性主要研究至少要出現多大的模型誤差，它才能在所規定的檢驗功效β0在顯著性水平為α0的檢驗中發現。在兩個備選假設下，可靠性理論主要研究的是不同備選假設下模型誤差的可區分性（可區分性理論）。弗斯特勒爾（1983）指出兩個檢驗量之間的相關系數可作為衡量可區分性的指標。李德仁教授在其博士論文中從兩個多維備選假設的情況下，導出了檢驗量之間的總體相關和最大相關，并進而導出了可發現且可與它種模型誤差相區分的模型誤差下界值。

鑒于在前述質量控制模型中以類似巴爾達的數據探測法來探測周跳和機動加速度，因而在下面的可靠性研究中主要考慮備選假設為一維時的內部可靠性分析。

首先考慮單個一維備選假設的情形。

對于單個方向機動加速度，有零假設H0：不存在機動加速度

備選假設Ha：存在一個方向的機動加速度

根據內部可靠性理論，可發現的機動加速度下界定義為

式中，δ0為非中心化參數，它可在給定顯著水平α0和檢驗功效β0下由標準化正態分布表求出。同樣對于單個觀測值粗差，有

零假設H0：不存在觀測值粗差

備選假設Ha：存在一個觀測值粗差可發現觀測值粗差的下界定義為：

當僅選擇當前時元的預報殘差進行檢驗，即采用局部一維定位檢測時，k=l，b，d分別定義為：

對于兩個一維備選假設，即

H0：無機動，無觀測值粗差

Ha1：存在一個方向機動加速度

Ha2：存在一個觀測值粗差

此時，內部可靠性要研究發現并區分兩類模型誤差的能力。可區分性取決于兩個備選假設之間的相關系數。單個方向機動加速度和單個觀測值粗差檢驗統計量的相關系數定義為

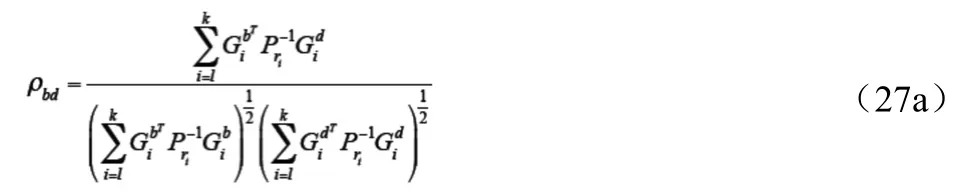
在k=l時，即選用統計量為局部一維定位統計量時

相關系數越大，則模型誤差的可區分性越差，當ρbd=1時，機動加速度與觀測值粗差不可區分。根據相關系數ρbd可以查表得到可區分性放大倍數Kρbd。該值表示由于相關引起的非中心化參數的放大倍數，更具體地講，它代表可區分且可發現的模型誤差下界為可發現模型誤差下界值的多少倍。

可發現且可與單個機動加速度區分的觀測值粗差下界為

可發現且可與單個觀測值粗差區分的機動加速度下界為

研究中發現，對于本節的濾波模型，內部可靠性主要與動態噪聲QK和觀測噪聲RK有關，在RK一定的情況下，隨著給定QK的增大可發現機動加速度和觀測值粗差的下界呈增大趨勢，而機動加速度與觀測值粗差的相關系數則呈減小趨勢。對于相同的QK，當觀測值精度較高時，可發現機動加速度和觀測值差的下界值較小。

3.2 可靠性分析實踐

下面以1996年8月14日在哈爾濱進行的一次秒采樣率機載GPS動態定位為例予以說明（如表1～表6所示）。該次定位中所采用的機載GPS信號接收機和基準接收機均為Trimble 4000SSE雙頻接收機。表1～表5為采用局部檢驗量時的內部可靠性分析，其中各量和計算均只采用濾波遞推估計10個時元后的一個時元（GPS時間288880s）的數據（該時元PDOP=2.8，共觀測下列6顆衛星：PRN26，06，27，16，17，18。其中PRN26號衛星高度角最大，其他衛星分別與它構成雙差觀測值）。表3～表4為采用寬巷觀測值進行濾波計算時的內部可靠性分析數據，表4～表5為采用L1單頻觀測值進行濾波計算時的內部可靠性分析數據。計算中假定L1，L2載波相位量測精度等于0.025周，因而對于L1雙差觀測值，有協方差陣

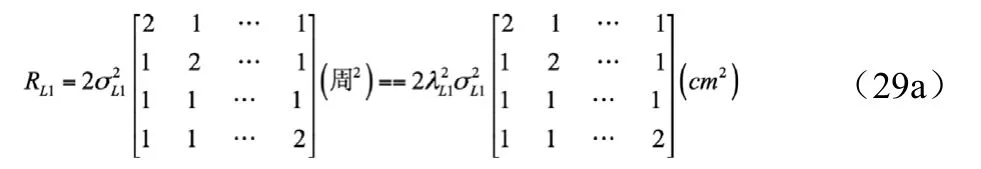
對于寬巷雙差載波相位觀測值有

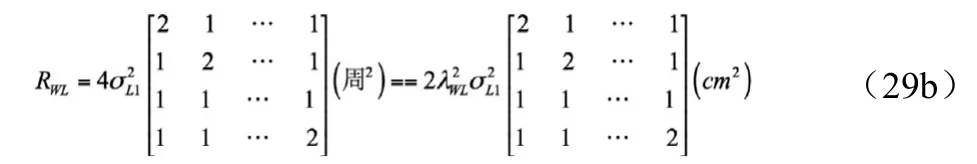
式中，λL1，λWL分別為L1載波相位和寬巷載波相位的波長（單位：cm）。

表1 QK與可發現機動加速度關系（寬巷）

表2 QK與可發現觀測值粗差的關系（寬巷）

動態噪聲協方差陣定義為

Q為標量，在各種QK陣設計中分別選取Q=le-8，le-4，le-2，0.1，1，10，100。各表計算中選取δ0為顯著性水平a0=0.1%，檢驗功效為80%時的非中心化參數δ0=4.13。

由表1可知，當RK一定時（寬巷觀測值），隨QK設定值的增大可發現機動加速度下界值呈增大趨勢。當Q=10時，可發現機動加速度下界約為重力加速度的2.6倍，超過了絕大多數運動載體的最大機動能力。而當Q=le-8時，所能發現的機動加速度下界約為0.2～0.4m。這是由于寬巷觀測量測量噪聲較大引起的。當選擇觀測噪聲較小的觀測量L1載波相位時，對應相同的QK可發現的機動加速度下界相對較小。

表3 QK與相關系數

表4 QK與可發現機動加速度關系（L1）

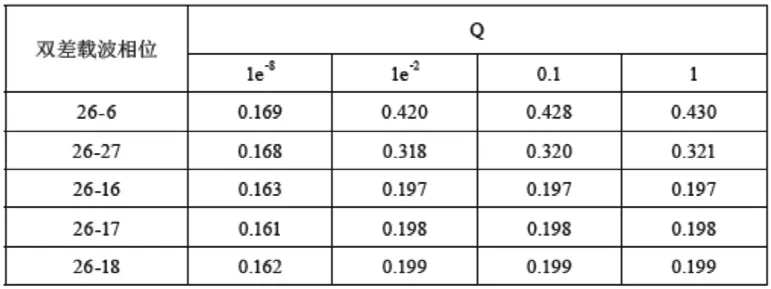
表5 QK與可發現觀測值粗差（L1）

從整體上看（尤其是QK較大時），局部檢驗量對機動加速度不敏感，這是前面提到的采用局部檢驗量時會產生機動探測延遲的主要原因，為了較好地探測機動，應考慮采用全局檢驗量。

由表2可知，RK一定QK增大時，可發現的載波相位粗差的下界也呈增大的趨勢，但增大速度明顯比可發現的機動加速度下界要慢，而且呈現出一種飽和趨勢。在Q≥0.1增大速度明顯變慢，對于不同的雙差載波相位，可發現觀測值粗差的下界值不同。更值得注意的是對于各種Q值可發現的粗差下界均小于1周，即1周大小的周跳是完全可以發現的。而此時我們所采用的僅是局部定位檢驗統計量，這也是盧剛（1991）認為僅利用局部檢驗量就可以探測出小周跳的原因。

比較表5和表2還可以發現，當選擇觀測精度較高的L1觀測值時，可發現粗差的下界值更小，隨QK的增大趨于飽和的速度更快，因而探測周跳的能力也更強。

表3中未列出機動加速與所有雙差載波相位的相關系數，僅列出了X、Y、Z方向與雙差載波相位相關系數值的最大值。表中第一列的“/”上為機動加速度方向，“/”下為對應最大相關系數的雙差載波相位衛星號。從表中可知，當Q較小時相關系數很大，甚至大到0.977。而隨著Q的增大，相關系數呈現逐漸減小的趨勢。而與可發現的機動加速度和粗差的趨勢正好相反。在由相應的相關系數查表得到可區分性放大倍數并乘以表3中可發現粗差下界值后可得到可與機動加速度區分且可發現的粗差下界值（見表2中“-”下方）。相應的區分可能性1-γ0選為95%。這一可區分且可發現的粗差下界值仍小于1 周，這表明即使對于1周的周跳也是可以發現并與機動加速度相區分。

以上實際是處理大量高精度GPS動態定位內部可靠性分析的基本特點。根據上述實例分析，可以得到以下幾個基本結論：

（1）對于周跳的探測，可僅采用局部檢驗量。由于載波相位量測精度高，即使動態噪聲選擇得較大，僅采用局部檢驗量，周跳均可發現且與機動加速度相區分，觀測量精度越高（RK越小）周跳的探測能力越強。

（2）對于機動加速度的檢測，應采用全局檢驗量。局部檢驗量對機動加速度的檢測不甚敏感。當采用多個時元構造全局檢驗時，隨著選擇時元數的增多，機動加速度檢測能力逐步增強。

（3）當QK較大時，可發現機動加速度下界值往往會超過運動載體的最大機動能力，然而此時對周跳探測能力仍優于1周。此時，可不必考慮對機動加速度的檢測，而僅用數據探測法檢測周跳。

表6 采用全局檢驗量時QK與可發現機動加速度關系（寬巷）

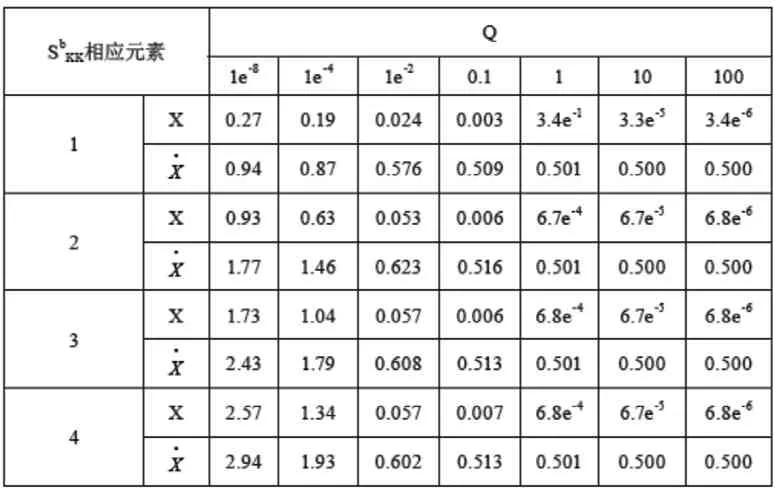
表7 SbKK相應元素（寬巷）

3.3 外部可靠性研究

外部可靠性研究的是不可發現的模型誤差對平差結果的影響。在對周跳進行修正后，僅存在機動加速度，此時機動加速度時濾波值的影響為：

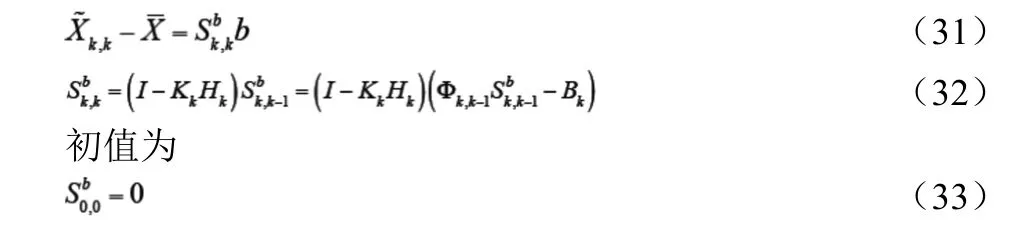
由式（31）可知機動加速度對濾波值的影響是由機動加速度與中相應元素相乘得到的，由于直角坐標系軸垂直的，因而沿X、Y或Z軸方向的單方向機動加速度，僅影響該方向的坐標和速度。

仍采用與檢驗內部可靠性相同的數據，采用寬巷觀測值，利用式（31）進行了外部可靠展性分析（表7）

表7中列出了與X方向位置、速度濾波估計偏差有關的中相應的元素（K=1，2，3，4）。由表列數據乘以X方·向機動加速度，可以得到這幾個時元的X，X濾波估計偏差。由表列數據可知，當給定QK較小時（Q＜le-2）時，隨著時元數的增加，由機動加速度引起的位置、速度偏差呈遞增趨勢，機動加速度會引起濾波估計的變壞甚至發散。而QK較大時（Q＞0.1）時，隨著時元數的增加，由機動加速度引起的位置估計誤差趨于常值。此常值隨QK的增大逐漸趨于0。速度估計偏差則趨于機動加速度的1/2。此時濾波得到的速度估值實際上是該時元與前一時元速度的平均值，即存在機動加速度時，采用無偏差參數模型，速度濾波估計隨QK增大逐漸趨于平均速度。

以上實例可以作如下解釋：RK一定，當QK較小時，濾波增益也小，即過去觀測在濾波中的加權較大，此時濾波估計對過去觀測的依賴性大，在出現機動后，會引起估計偏差的增大。當QK較大時濾波對于過去觀測的依賴性或者說受過去觀測的影響也相對較小。在出現機動后濾波估計主要取決于當前的觀測，濾波估計偏差隨時元數增加的影響也較小，而且趨于較小的穩定值（濾波位置估計偏差趨于0）。另外，由于雙差載波相位觀測對速度的偏導數為0，即載波相位觀測量不直接對速度分量進行觀測。QK較大時，速度估計基本上由在時元和上一時元的位置求平均得到，此時的速度估計為平均速度，而不是當前時刻的瞬時速度

4 簡單、實用的高精度GPS動態定位濾波處理模型

由前述的內部可靠性研究可知，采用局部檢驗量周跳均可發現且與機動加速度相區分。觀測量精度越高，周跳探測的能力也越強。且當QK較大時，可發現機動加速度下界值往往會超過運動載體的最大機動能力，機動加速度的檢測應采用全局檢驗量。

由外部可靠性研究可知，在QK較小時不可發現的機動加速度會引起濾波估計變壞甚至發散，而QK較大時，隨時元數的增多，由機動加速度引起的位置估計誤差趨于常值，此常值隨QK的增大趨于零。隨QK的增大，速度估計偏差趨于機動加速度的1/2，即速度濾波估值趨于平均速度。

當我們不以測速為目的，而僅僅以確定各時元動態點位為目的時，可以不顧及機動加速度的影響，即可以不采用機動識辯動態模型而采用常速模型并假定較大的動態噪聲將機動加速度引起的速度擾動歸入動態噪聲之中。由于載波相位具有很高的量測精度，此時濾波位置估計仍具有很高的精度，且濾波不會發散。在多種機載GPS動態定位數據處理中發現，當選擇Q≥0.4，L1、L2載波相位量測精度分別假定為0.025周時，各次濾波結果中坐標分量相差僅在毫米級，圖7.2.1為一次秒采樣率機載GPS動態定位中，QK中元素Q分別選擇為0.4、1、4、10 時濾波結果中X坐標分量的互差。

基本以上內外可靠性分析以及在已知整周模糊度已知時載波相位觀測值可轉換為高精度測相位偽距的特點，提出了一種簡單實用的高精度GPS動態定位濾波處理模型。由于狀態定位向量中不包含模糊度參數，稱之為無模糊度參數濾波模型。

無模糊度參數濾波模型由式（35）定義：

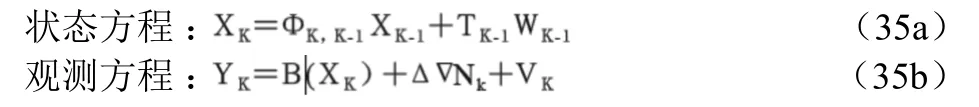
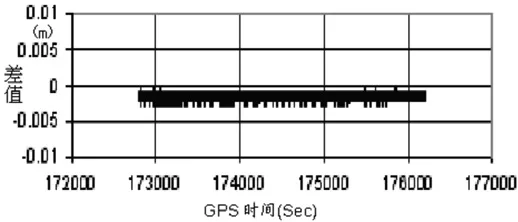
圖1 不同QK下濾波差值

系統動態噪聲和量測噪聲的統計特性假設如下：

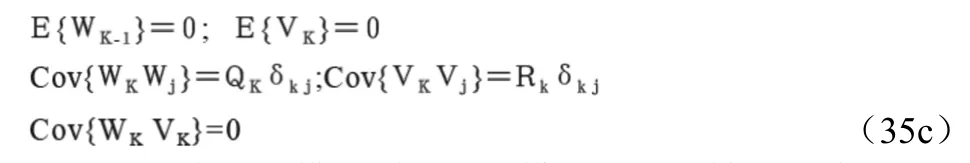
式（35a）中動態模型采用常速模型。狀態轉移矩陣ΦK，K-1和干擾矩陣TK-1定義如下：

式中，I3為3×3維單位陣；ΔT為采樣時間間隔。其中，狀態向量為；xK，yK，zK為動態接收機天線在WGS-84地心坐標系中的三維位置，為動態接收天線的三維速度。在該模型中選取較大的模型噪聲QK，根據內部可靠性分析可探測的機動加速度下界值也大，從而相應的局部檢驗量對機動加速度不敏感。根據外部可靠性分析，機動加速度對濾波位置影響很小，而動態定位所需要的也只是各觀測時元的動態位置，因而選擇較大的QK不會因機動加速度降低動態定位的精度。

在此模型下，關鍵的問題是周跳的探測與修復。周跳的探測和修復按如下步驟進行：

第一步：根據預處理中周跳探測結果，首先刪除有周跳標記衛星所對應的雙差載波相位觀測值。

第二步：計算預報殘差及其協方差陣，然后采用式（21）進行局部示警檢驗。當＜F時，認為剩余雙差觀測值沒有周跳，轉到第五步。當≥F時，則剩余雙差觀測值中仍存在周跳，但無法確定在哪個觀測值上，為此需進行進一步檢測。

第三步：對所剩余雙差觀測值分別采用式（24b）進行局部一維定位檢測，并刪除數值最大檢驗量所對應雙差觀測值。

第四步：重復第二、三步直到局部示警檢驗量TG1＜F。

第五步：利用剩余雙差觀測值進行濾波計算。

第六步：檢查周跳標記，并根據濾波位置反求有周跳標記雙差載波相位觀測值的周跳數。

以上周跳的探測的修復基本上采用盧剛和魏明的周跳探測、修復方法，并基于內外部可靠性研究拋棄了并無多大作用而耗力的機動加速度檢測部分，簡化了處理模型。研究表明以上周跳探測和修復方法對于少量周跳（無周跳的雙差載波相位觀測值數量≥3）是十分有效的，若周跳衛星很多，連續跟蹤的衛星數＜4時，以上方法則無法完全修復周跳，此時需利用在航模糊解算方法重新求各衛星整周模糊度，這和盧剛的研究結果也是一致的。

5 數值分析

5.1 周跳的探測與修復

根據上文所述模型，對無周跳數附加虛擬跳值后進行了周跳的探測和修復，所用數據為1996年8 月4日哈爾濱進行的一次秒采樣率機載GPS動態定位（表8，表9）。表8中數據為飛機靜止時的周跳探測與修復結果；表9中數據為飛機起飛后的周跳探測和修復結果。由于飛機在運動，因而各雙關載波相位的預報殘差較大，但此時仍有很好的周跳探測和修復能力，充分證明了上文模型的有效性。

5.2 與GPSur vey軟件解算結果比較

Ttimble公司為其測量型接收機配備了高精度定位數據處理軟件包GPSurvey，它可以處理靜態和動態數據，為了驗證本文算法的正確性，選擇了一套動態定位數據分別采用文方法和GPSurvey軟件進行了處理，其差值見圖2（圖中虛線表示基準站與流動站的距離，實線為解算差值）。從該圖中可以看出，即使距離遠達100km，本文方法與GPSurvey軟件解算差值也不超過5cm，即不超過0.5ppm，這也證明了本文方法的正確性。

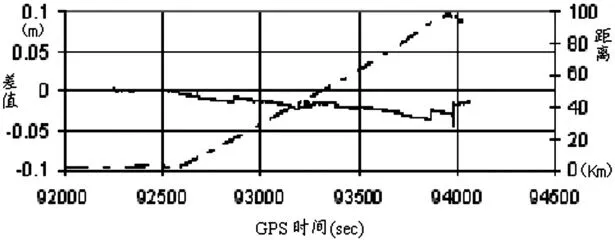
圖2 無模糊度參數解算與GPSurvey軟件解算成果比較

[1] 劉基余.GPS衛星導航定位原理與方法（第二版）.北京：北京科學出版社，2008.6.

[2] Lachapelle，G.，GPS Theory and Applications，University of Calgary，Fall 2000，PP.310.

[3] 劉基余，陳小明，李德仁等.GPS Kinematic Carrier Phase Measurements for Aerial Photogrammetry，ISPRS Journal of Photogrammetry and Remote Sensing，Vol.51，No.5，1996，P.230～242.