武術套路動作分解過程的模式識別方法
劉猛猛
摘 要: 針對傳統的武術套路分解過程中動作分解模式識別時,存在動作無法連續識別缺少細節特征的問題,提出武術套路動作分解過程中,使用NReJ3D技術對模式識別方法進行優化。通過分析識別結構框架,引入NReJ3D技術對人體細節特征進行采集,通過嵌入映射分析為模式匹配程度分析提供依據,利用低維運動空間實現模式匹配識別,實現模式識別方法的優化。通過實驗結果表明,改進識別方法能對連續動作進行高清晰度識別,細節特征提取較多,具有一定優勢。
關鍵詞: 武術套路; 動作分解; 模式識別; 細節特征; 特征采集; 低維運動空間
中圖分類號: TN911?34; TP393 文獻標識碼: A 文章編號: 1004?373X(2018)08?0171?03
Abstract: In allusion to the problems that the continuous actions cannot be recognized and it lacks detail features in the traditional pattern recognition of action decomposition during the decomposition process of Wushu routines, the idea of using NReJ3D technology to optimize the pattern recognition method during the action decomposition process of Wushu routines is proposed. NReJ3D technology is introduced to collect the detail features of human body by analyzing and recognizing structure framework. Map analysis is embedded to provide the basis for analysis of pattern matching degree. Low dimensional motion space is used to realize the pattern matching recognition and optimization of pattern recognition method. The experimental results show that the improved recognition method can recognize the continuous actions with high resolution and extract more detail features, which has certain advantages.
Keywords: Wushu routine; action decomposition; pattern recognition; detail feature; feature acquisition; low dimensional motion space
武術套路動作分解過程中,傳統動作模式識別方法使用RGB圖像的形式進行識別,識別內容包含動作信息以及武術套路,但傳統方法對光線的變化、視角位置、動作頻率等因素很敏感[1]。人體呈現鏈式結構時,武術套路動作特點往往表現在關節位置的變化上,由于識別方法的限制,很大程度上不能對連續動作進行識別[2]。傳統識別方法在低維運動空間里人體動作識別計算難度很高,模式識別的有效性不足45%。雖然在低維運動空間里描述人體運動需要復雜的動態數據,但是武術套路動作會受限于運動力學的影響。針對上述背景,本文提出武術套路動作分解過程的模式識別方法,對低維運動空間下人體動作識別結構進行優化設計,能夠有效解決傳統模式識別方法中角度、光感等因素的限制。利用NReJ3D技術作為人體細節特征表達方式,能夠對細節變化保持較高的敏感度,對嵌入方式進行重新優化,達到低維運動空間映射的連續性,以此解決傳統方法無法連續識別的問題。為了驗證本文提出的模式識別方法的有效性,模擬應用過程進行試驗,用傳統模式識別方法與本文識別方法相比較,通過實驗結果表明,本文提出武術套路動作分解過程的模式識別方法,能對連續武術套路動作進行識別,具有較高的細節刻畫能力。
1 武術動作模式識別框架優化設計
本文對模式識別框架進行優化設計,使用自身反饋的形式進行優化,改變傳統順勢性識別模式,利用模塊自身特點進行識別分析[3]。本文設計武術動作模式識別框架如圖1所示。
1.1 基于NReJ3D技術的動作特征采集
本文使用NReJ3D技術進行細節上的模式識別以及細微動作表達。由于武術套路動作在低維度運動空間里的變化,往往表現在關節位置的變化上。關節之間反差往往體現在關節角度以及相對位置的變化。NReJ3D技術的特征表達方式是使用多個節點數據進行細節描述,節點數據所描述的信息往往大于直接用3D節點數據的特征表達形式[4],比如抬動左腿和抬動右腿。如果直接用傳統表達方法,抬動左腿需要使用17個3D節點數據進行動作套路特征表達;抬動右腿需要使用20個3D節點數據進行動作套路特征的表達,抬動左腿和抬動右腿的實際差別僅是3個數據節點[5]。其余的數據節點信息沒有發生實質性變化,這樣很難識別出細節的動作。使用NReJ3D技術能把節點數據轉變為描述性節點數據,有一個描述性數據發生變化,可能是維度和角度的多重變化。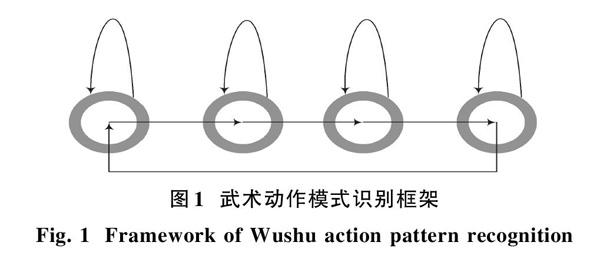
本文導入NReJ3D技術,從武術套路動作分解數據中得到3D節點數據,使用描述性數據對3D節點數據進行描述,整個描述過程中對動作細微變化進行表達,能準確識別動作細微變化。使用NReJ3D技術進行動作特征表達時,首先需要對武術套路動作進行特征分析,將人體轉變成為一個剛性連接的方位移動變量[6]。能描述動作的平移、縮放及多維度變化,且可以無視角度變化以及光線變化。假設武術套路動作在時刻[t]下,利用NReJ3D技術所描述的節點數據為[i],在三維坐標[xit,yit,zit]中,以人體的非變化區域為中心,對動態數據節點[h]變化進行描述。其中描述節點滿足[ii≠h]條件時,可以把動態數據節點[h]的數據變化差作為動態特征的一部分,即:

1.2 嵌入映射
經過上述NReJ3D技術處理后的武術套路動作,能夠在低維運動空間里把動作序列有效地映射到數據維度空間去[7]。但是傳統的映射方法無法映射出本文引入NReJ3D技術處理后的節點數據。需要對嵌入映射過程進行修訂。在實際操作中,選擇原有的武術套路動作三維數據集以及描述多維動作數據集放在一起重新進行嵌入式導入。但武術套路動作三維數據集中包含的數據量過于龐大,因此本文使用Roweis嵌入的方式,進行嵌入映射計算。
通常狀態下,對于一個武術動作的測試點[y]來說,本文使用三個步驟計算,便可以將映射嵌入低維運動空間里對應位置[x]上。在描述多維動作數據集中,找到與武術動作的測試點[y]最近的k個識別映射點,假設識別映射個數為[yii=1,2,…,k],然后計算器對應的多維權重值[wj],并對其進行導入處理[8]。由于[y]的k個近鄰點[yii=1,2,…,k],動作在低維運動空間里所對應的點分配映射為[xii=1,2,…,k],那么可以說[y]在低維運動空間里所對應的識別映射為[x=xiwi,i=1,2,…,k],至此完成嵌入映射過程。
1.3 模式匹配程度分析
經過上述的NReJ3D技術處理以及嵌入映射,武術套路動作基本已經識別完成,將相似度高的兩個武術套路動作進行匹配識別。測定識別動作數據與武術套路數據集相似度,在低維運動空間里實現匹配識別。本文使用Hausdorff比對方式進行度量(由在低維運動空間下,假設所有識別匹配動作點與每個武術套路運動模式匹配過程是均值狀態),即:
2 實驗分析
2.1 實驗參數設計
本文實驗對象為模式識別方法,通過量化后的數據無法實現對比,需采用描述性數據進行對比。使用描述性數據必須對數據進行標準設定,本文對人體進行數據分解設置,實驗參數如表1所示。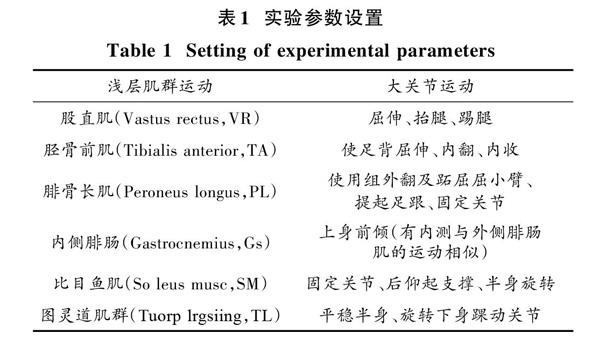
2.2 實驗結果分析
實驗過程分別選取兩項肌肉模式識別數據,兩項關節轉變識別數據,實驗識別結果見圖2。從圖2中能夠清晰識別肌肉的變化情況,并且具有一定的細節刻畫能力。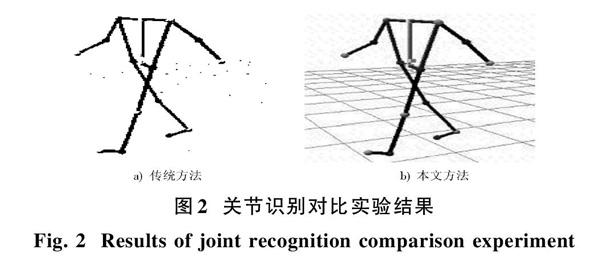
圖2為本文識別方法與傳統識別方法在關節上的對比結果,傳統方法下,可看出關節大致變化趨勢,但非聯動性關節表現力不清[10]。本文使用NReJ3D技術對關節的細節進行重點刻畫,能夠清晰地看清每個關節的趨勢變化。
圖3為SGY環幀率對比結果。SGY環幀率與識別精準度成正比關系,SGY環幀率越高說明識別精準率越高。通過圖3可知,雖然傳統方法開始略好于本文提出的識別方法,但后續的實驗過程中,沒有高于本文提出的方法,為此本文提出的識別方法更具有識別能力。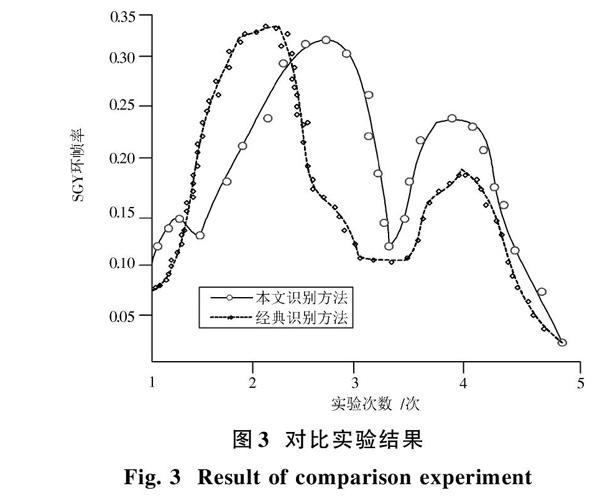
3 結 語
本文提出武術套路動作分解過程的模式識別方法。重新設計識別結構框架,利用NReJ3D技術對人體細節進行描述性的表達,對嵌入式映射過程重新設計,實現動作連續性識別表達,利用低維運動空間實現模式匹配識別。希望通過本文的研究能夠提升武術套路動作分解過程的模式識別能力。
參考文獻
[1] 阮羚,李成華,宿磊,等.基于奇異值分解的局部放電模式識別方法[J].電工技術學報,2015,30(18):223?228.
RUAN Ling, LI Chenghua, SU Lei, et al. Pattern recognition for partial discharging using singular value decomposition [J]. Transactions of China electrotechnical society, 2015, 30(18): 223?228.
[2] 王俊峰.基于圖像識別的武術動作分解方法研究[J].現代電子技術,2017,40(15):33?36.
WANG Junfeng. Research on Wushu movement decomposition method based on image recognition [J]. Modern electronics technique, 2017, 40(15): 33?36.
[3] 田潤鋒.武術套路動作節奏學習方法探究[J].青少年體育,2016,31(12):36?37.
TIAN Runfeng. Inquiry learning method of Wushu movement rhythm [J]. Youth sports, 2016, 31(12): 36?37.
[4] 律方成,謝軍,李敏,等.局部放電稀疏分解模式識別方法[J].中國電機工程學報,2016(10):2836?2845.
L? Fangcheng, XIE Jun, LI Min, et al. Partial discharge sparse decomposition pattern recognition method [J]. Proceedings of the CSEE, 2016(10): 2836?2845.
[5] 孟巧玲,易金花,喻洪流,等.基于肌音信號的上肢康復訓練動作模式識別方法[J].中華物理醫學與康復雜志,2015,37(11):876?878.
MENG Qiaoling, YI Jinhua, YU Hongliu, et al. Action pattern recognition method of upper limb rehabilitation training based on muscle tone [J]. Chinese journal of physical medicine and rehabilitation, 2015, 37(11): 876?878.
[6] 劉玉敏,周昊飛.基于多特征的PSO?MSVM動態過程質量異常模式識別[J].計算機應用研究,2015,32(3):713?716.
LIU Yumin, ZHOU Haofei. Recognition of quality abnormal patterns for dynamic process based on multi?features with PSO?MSVM [J]. Application research of computers, 2015, 32(3): 713?716.
[7] 趙漫丹,郝向陽,張振杰.一種基于層級分類策略的復雜模式識別方法[J].計算機應用研究,2016,33(8):2320?2323.
ZHAO Mandan, HAO Xiangyang, ZHANG Zhenjie. Method of complicated pattern recognition based on hierarchical classification strategy [J]. Application research of computers, 2016, 33(8): 2320?2323.
[8] 韓雪.武術動作分析及能量轉化模型的應用[J].中學物理教學參考,2015(24):66?67.
HAN Xue. Analysis of Wushu movements and application of energy transformation model [J]. Teaching reference of middle school physics, 2015(24): 66?67.
[9] 宋偉,劉玉萍,王麗娜.高水平競技武術套路比賽運動員技術特征分析[J].北京體育大學學報,2015(5):135?140.
SONG Wei, LIU Yuping, WANG Lina. Analysis of high level Wushu competition athletes′ technical characteristics [J]. Journal of Beijing University of Physical Education, 2015(5): 135?140.
[10] 劉和臣.運動員動作三維視覺圖像準確識別仿真研究[J].計算機仿真,2016,33(8):369?372.
LIU Hechen. Athletes action three?dimensional visual images accurately identify simulation research [J]. Computer simulation, 2016, 33(8): 369?372.

