雙向內外管差壓流量計參數優化與數值模擬

王太飛，孟　江，吉　鵬

(中北大學機械工程學院，山西 太原 030051)

0　引言

流量儀表技術在19世紀中葉到20世紀迅速發展。人類社會對流量測量的需求加快了流量儀表的更新換代[1]。直到近幾十年，新材料和新技術的出現，使該行業實現了跨越式發展。在新型流量計層出不窮的時代，傳統的差壓式流量計仍占有一席之地。差壓式流量計是目前在工業測量中應用較為廣泛的流量儀表之一[2]。

對于近幾年流行的V錐差壓流量計，其優點是要求直管段較短、抗臟污等。但是V錐差壓流量計難以兼顧較高的精確度和較低的壓力損失，因此其并不是能源監測流量儀表的最佳選擇。為了減少測量能耗及保證精確測量，對差壓流量計進行了改進，如設計了內外管差壓流量計[3]。內外管差壓流量計能夠在不改變總流通面積的前提下，在同一截面上獲得差壓，對管道內流體的流型影響較小，消除了節流件前后摩阻壓降對差壓信號的影響，達到了節能的效果；在相同的流量下，其獲得的差壓遠大于傳統差壓式流量計，提高了信號的靈敏度；其節流方式對流體的擾動比傳統流量計小，提高了差壓信號的穩定性[4-6]。

雖然對內外管差壓流量計的結構設計已有一些研究和優化，但仍存在一些問題。如文獻[7]和文獻[8]，雖然都獲得了結構優化結果，并能有效地進行流量測量，但在結構相似的內外管流量計中流體方向相反，且取壓位置分別為節流件的入口和出口處。為提高內外管差壓流量計的實用性，解決內外管流量計在測量過程中流體流動方向和取壓口的爭議，設計了雙向內外管壓差流量計。該流量計可以不考慮流體流動方向，實現盲插安裝，且取壓口處信號更加穩定，為實際應用提供了便利。此外，對內外管差壓流量計的結構優化通常是選擇幾個數據模型進行對比，以選擇最優模型。為了得到準確的結構模型，本文利用二次回歸正交組合設計的試驗方法，并結合已有的模型數據，進行雙向內外管差壓流量計主要參數優化，得到確切的結構尺寸，為雙向內外管差壓流量計的進一步研究提供參考。

1　理論基礎

1.1　工作原理

雙向內外管差壓流量計與一般的差壓流量計原理相似，主要差異就是內外管取壓差。雙向內外管差壓流量計結構如圖1所示。其通過在流道2和流道1中取壓差來進行流量測量。

流體流過雙向內外管差壓流量計節流件時(可不考慮流體流動方向，以圖1中流體方向為例進行測量原理說明)，流體于截面Ⅰ被流道1和流道2分開。流體流至截面Ⅱ前，流道1對流體進行壓縮節流，使流體流速增大，壓力減小；流道2中流體擴散，使流體流速降低，壓力增大。流體在截面Ⅱ直管段流速和壓力都趨于穩定，并于截面Ⅱ處取壓差。流體流至截面Ⅲ時，流道1中流體擴散，使流體流速降低；流道2中流體被壓縮節流，使流體流速增大，壓力減小，最后匯于主管道。

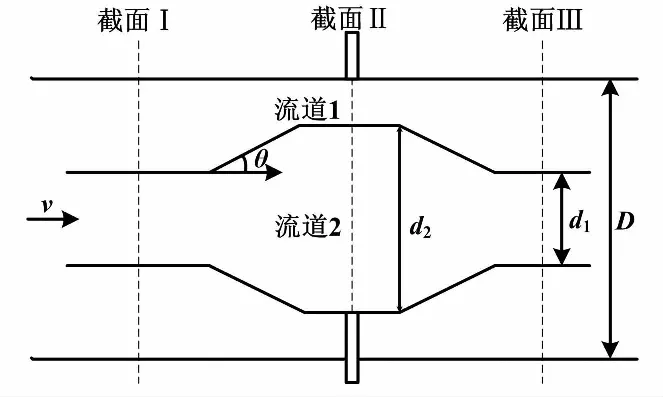
圖1　雙向內外管差壓流量計結構圖Fig.1　Structure of differential pressure flowmeter with　two-way internal and external tubes

流道1、流道2的連續方程為：

A11v11=A12v12=A13v13

(1)

A21v21=A22v22=A23v23

(2)

因為雙向內外管節流件為對稱結構，所以流體在流經截面Ⅰ、Ⅲ時，內外管的流體瞬時流速和壓力相等。由此可得雙向內外管差壓流量計在3個截面處的伯努利方程：

(3)

(4)

當流體流經節流件時，由于節流件的長度短、擴散角小、水頭損失小，通常會忽略水頭損失。則：

z1=z2=z3

(5)

由此可得出流體流入節流件前的流速：

(6)

考慮到流體的黏度以及安裝的支架對流場的影響，定義流出系數C。則流速可表示為：

(7)

式中：C為流出系數(一般為試驗標定)。

不可壓縮流體的體積流量可表示為：

(8)

式中：A為流道總截面積。

傳統差壓流量計體積流量的測量公式為：

(9)

可得雙向內外管差壓流量計的理論等效直徑比為：

(10)

壓差信號和壓力損失是差壓流量計的兩個重要參數，其決定了流量計性能的優劣，是流量計設計過程中需重點考慮的因素。對于雙向內外管差壓流量計而言，內外管壓差越大、前后壓差越小，則壓差信號越強、壓力損失越小、性能越優越。為衡量雙向內外管差壓流量計的性能，選擇引入壓損比φ作為衡量標準，即：

(11)

式中：ΔP內外為內外管壓差信號；ΔP前后為節流件前后永久壓損。

在雙向內外管差壓流量計結構參數優化和不同差壓流量計的性能對比中，壓損比φ越大，流量計性能越好，越能滿足工業生產的需要。

1.2　結構優化

本文采用二次正交回歸組合設計的試驗方法，利用二次正交回歸表設計9組異徑模型。然后，利用Fluent軟件進行雙向內外管差壓流量計的模型建立和數值模擬仿真。依據仿真所得的壓損比，建立回歸方程，對試驗結果進行優化。

2　模型仿真與回歸分析

依據對內外管差壓流量計以及噴射泵擴散角的優化研究[8-10]，選取外管道內徑D為27.2 mm、節流件擴散角θ為7°。為更直觀地顯示雙向內外管差壓流量計的具體結構尺寸并有效屏蔽不合理的模型結構，選定節流件大徑8≤d2≤23.2 mm、小徑和大徑之比0.4≤k≤0.8，并通過這2個因素確定雙向內外管差壓流量計的基本結構。

設定d2、k，建立正交組合試驗方案。通過Fluent軟件，依據試驗方案建模、仿真并計算得到壓損比，建立二元二次正交回歸組合設計表，并根據試驗結果建立回歸方程；然后對偏回歸系數進行顯著性檢驗，證明需要建立的回歸方程以及各偏回歸系數都能夠達到顯著水平；最后根據極值條件，確定最大壓損比下d2和k的值，得到壓差信號靈敏、穩定的雙向內外管差壓流量計的結構。

模型建立后，采取自動網格劃分。仿真條件設置如下：流體介質為水，為不可壓縮流體；工況的溫度為常溫20 ℃；依據d2、k建立正交組合試驗方案，并進行結構參數設置；管路水平放置，方向設置與圖1方向一致；入口速度為 1 m/s、3 m/s。仿真得到的壓損比為正交回歸表中的φ值，需再進行回歸分析與顯著性檢驗。

根據臨界雷諾數，判定管內為湍流狀態，仿真模型選擇2階標準模式的湍流模型。將管路流場仿真的入口邊界條件設為速度入口，并在速度入口的湍流參數設置中選擇湍流強度和水力直徑。其中：湍流強度為I=0.16(Re)-1/8，Re為水的雷諾數。出口條件選擇流出出口，其他參數同入口條件一致，壁面條件設置為墻壁，并采用比較適合解決穩態問題的半隱式壓力耦合方程組(semi-smplicit methool for pressure linked equations,SIMPLE)算法。在Fluent的后處理中，根據面積得到前后兩點和內外管取壓口四點處的壓力，求得壓損，并應用正交回歸組合的試驗方法進行優化計算。

取d2、k為正交回歸組合設計中的兩個因素，故因素數m=2，去零水平試驗次數m0=1，星號臂長γ=1。由此可得該試驗的因素水平編碼表，如表1所示。

表1　因素水平編碼表Tab.1　Factor levels coding

在Fluent中建立相應的仿真模型，并通過改變d2、k的值，共設計9組試驗。在仿真的后處理中計算出相應的壓損比，并記錄在如表2所示的二元二次回歸正交組合設計計算表中。表2中：z1與z2分別是d2與k的編碼值。

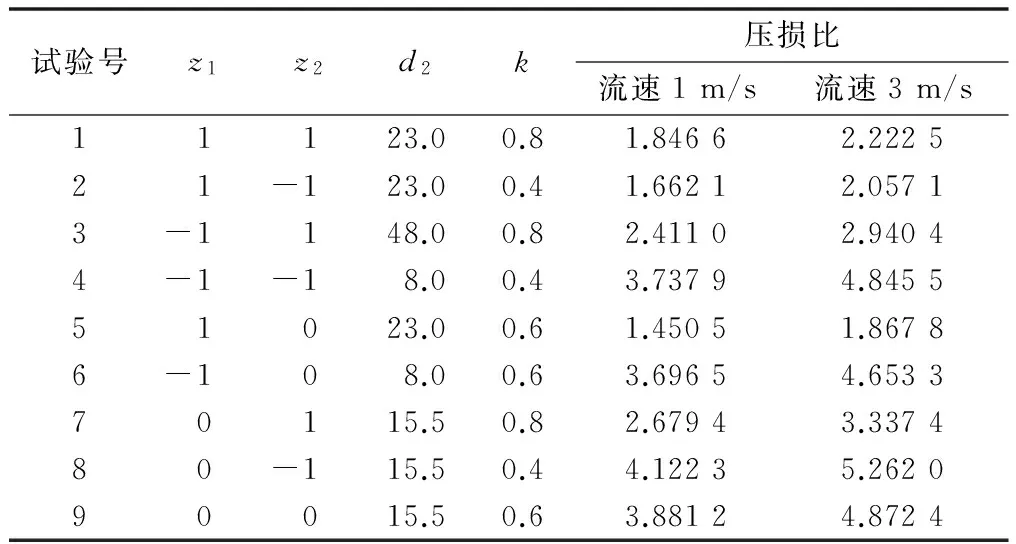
表2　二元二次回歸正交組合設計計算表Tab.2　Calculation table for binary quadratic regression orthogonal design

設定入口速度為1 m/s、3 m/s，在雙向內外管流量計的入口、出口和節流件管中、管外設置4個取壓點，依據式(11)求解出對應模型的壓損比；利用回歸分析，計算出9組模型的回歸方程；根據極值必要條件，求解出最大壓損比下對應的d2、k(節流件大徑值、節流件小徑與大徑比的值)，由此得出最優模型。

當入口速度為1 m/s時，φ的二次回歸方程為：

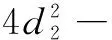
(12)

式中：8≤d2≤23.2；0.4≤k≤0.8。

采用約束優化算法得到最大壓損比φ=4.227 0，對應的最優尺寸參數為d2=11.178 9、k=0.4。

當入口速度為3 m/s時，φ的二次回歸方程為：

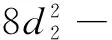
(13)

式中：8≤d2≤23.2;0.4≤k≤0.8。

采用約束優化算法得到最大壓損比φ=5.423 2，對應的最優尺寸參數為d2=11.130 5、k=0.4。

對比入口速度1 m/s和3 m/s最優模型尺寸。考慮到數據計算誤差，可以將2組最優模型尺寸視為一致。同時，該結果也說明了在模型尺寸最優的情況下，低速流場中任何速度的流體，在該模型下的壓損比都可以達到一個最優值。經圓整，選取節流件大徑11.15 mm，節流件小徑與大徑之比為0.4，節流件小徑為4.45 mm，作為雙向內外管差壓流量計的最優模型。

3　流量計性能對比

為了研究雙向內外管差壓流量計在流量測量方面的特性，在同等工況下，選擇最優尺寸模型，建立雙向內外管差壓流量計模型、內外管差壓流量計模型(流體進入節流件方向不同的兩種情況)進行模擬仿真，并對比3種模型的前后壓損、節流件內外管壓差和壓損比等特性。

應用Fluent軟件，分別建立3種流量計的模型。其中，入口邊界條件設為速度入口。分別取0.5 m/s、1 m/s、1.5 m/s、2 m/s、3 m/s這5個速度等級，設置迭代步數1 000，步長為1。其他設置依照前文雙向內外管模型優化時的方法，此處不作贅述。應用Fluent軟件查看3種流量計模型在各個入口速度的壓力云圖時，三者在壓差取壓點附近的壓力穩定。可以直觀地看到：雙向內外管差壓流量計與內外管差壓流量計(大管徑流入)這2個仿真模型的內外壓差明顯，而另一個模型的內外壓差對比并不明顯。在后續處理中，計算出三者的壓損比。為了更直觀地對比壓損比的變化，將計算結果繪制成折線圖，不同速度下3組流量計的壓損比折線圖如圖2所示。

圖2　壓損比折線圖Fig.2　Line charts of pressure loss ratio

根據圖2可以看出，在5級速度下，隨著流速的不斷增大，3組流量計的壓損比都在增大。雙向內外管差壓流量計的壓損比大于另外2組內外管差壓流量計(不管流體從節流件哪個方向流入)，說明雙向內外管差壓流量計靈敏度更高，在測量過程中雙向內外管差壓流量計性能優于普通的內外管差壓流量計。此外，從節流件小管徑流入的內外管差壓流量計的壓損比最小。將壓力損失同樣繪制成折線圖，不同速度下3組流量計的壓力損失折線圖如圖3所示。

圖3　壓力損失折線圖Fig.3　Line charts of pressure loss

在5級速度下，隨著流速的不斷增大，3組流量計的前后測點壓力損失都在增大；但雙向內外管差壓流量計的前后測壓點的壓力損失小于另外2組內外管差壓流量計(不管流體從節流件哪個方向流入)。由此可知，雙向內外管差壓流量計能夠在測量過程中減少能量損失。該設計符合現代社會提倡的節能環保理念。在能耗方面，雙向內外管流量計更加節能，表現出更多的測量優勢。

4　結束語

由于內外管差壓流量計在流體方向和取壓位置的選擇上存在爭議，本文設計了雙向內外管差壓流量計。該流量計可實現盲插安裝，且取壓口的信號更加穩定。相對于通過數組結構模型數據進行對比選擇出最優結構模型，本文將Fluent流體仿真軟件與二次正交回歸組合設計的試驗方法相結合，能夠準確地選擇最優結構模型。以雙向內外管差壓流量計中節流件大徑、節流件小徑與大徑之比為參數，正交組合出9組模型，利用Fluent對雙向內外管差壓流量計進行建模仿真，求得壓損比。然后，正交回歸分析得到回歸方程，計算得到節流件大徑為11.15 mm、節流件小徑為4.45 mm、節流件小徑與大徑之比為0.4的最優模型，并通過仿真分析計算了最優模型的壓損比。其壓損比大于之前9組模型的壓損比，驗證了利用正交回歸分析優化的可靠性。

將雙向內外管差壓流量計與普通內外管差壓流量計進行對比分析。結果表明，前者的壓損比大于后者，測量性能更加優越。雙向內外管差壓流量計的壓力損失明顯小于單向內外管差壓流量計，流體動能損失更小，符合工業生產中的節能理念。在國家提倡節能減排的背景下，擁有節能環保和測量精準的雙向內外管差壓流量計，具有良好的工業實用價值，可以在化工與石油領域中進一步推廣。

參考文獻:

[1] 解海艇,黃富貴.流量儀表技術的發展趨勢[J].自動化儀表,2013,34(4):69-72.

[2] 翟小金,沈新建,王光磊,等.新型差壓式流量計性能研究[J].自動化儀表,2017,38(1):81-85.

[3] PENG L L,DONG H C,SHI Y,et al.Gas-liquid two-phase flow detection techniques based on internal and external tube differential pressure flowmeter[J].Applied Mechanics & Materials,2014(6):363-369.

[4] 許德福,王濤.淺談差壓式流量計的工作原理及選型[J].廣東化工,2013,40(251):152-153.

[5] 周民,劉鐵軍,謝代梁.差壓式雙錐流量計研究及實驗分析[J].自動化與儀表,2016,31(1):14-18.

[6] 方立德,張垚,王小杰,等.新型內外管差壓流量計濕氣測量模型研究[J].傳感技術學報,2013,26(8):1173-1177.

[7] 李小亭,王小杰,方立德,等.新型內外管差壓流量計特性研究[J].儀器儀表學報,2012,33(10):2371-2379.

[8] 范玉良,孟江,趙贊,等.內外管壓差流量計的壓力損失[J].機械設計與研究,2014,30(1):98-100.

[9] MENG J,LIU Z P,AN K,et al.Simulation and optimization of throttle flowmeter with inner-outer tube element [J].Measurement Science Review,2017,16(2):68-75.

[10]龍新平,王豐景,俞志君.噴射泵內部流動模擬與其擴散角優化[J].核動力工程,2011,32(1):52-57.