基于四桿曲柄滑塊機構的可展機構設計

孔凡臣，　孫建偉，2＊，　張邦成,2，　張　煒

(1.長春工業大學 機電工程學院， 吉林 長春　130012;2.長春工業大學 汽車工程研究院， 吉林 長春　130012)

0　引　言

由于運載火箭受到體積和成本的限制，因此，占用空間小、質量輕的可展機構被大量應用于星載天線和空間結構支撐等方面。可展機構具有收攏和展開兩種穩定的狀態。當機構處于運載階段時，機構通過折疊收攏的方式來減小自身尺寸，從而使其能夠被放置于運載火箭內，當進入預定工作位置時，機構再由收攏狀態展開形成星載天線或空間機構支撐結構[1]。

隨著航天技術的不斷發展，對通訊、衛星定位、對地觀測和深空探測等設備的精度和體積提出了更高的要求。對于可展機構的研究已成為機構學的熱點研究內容之一。

國內外眾多學者圍繞該問題進行了深入的研究。比較典型的可展機構有美國TRW公司研制開發的太陽花(Sunflower)天線；劍橋大學可展結構試驗室研制的SSDA(Solid Surface Deployable Antenna)以及德國Dornier公司和歐空局ESA聯合研制的DAISY(Deployable Antenna Integral System)[2]。廖啟征[3]等提出了一種由剛性桿件和柔性鉸鏈組成平面放縮機構的方法，為平面任意形狀可展式機構的設計以及機構的慣性力平衡設計提供了一種通用性方法。李端玲[4]等基于球面剪叉單元構造出了各種球面剪叉可展機構，這些機構可保持在球面上運動，具有繞通過球心的軸線轉動的特點，有收縮和展開的功能。楊毅[5]等基于7 桿閉環機構提出一種新型四棱錐單元,并將其作為一個基本可展機構單元,設計出了一種全新的大型可展機構,并分析了單元的自由度、運動學和奇異性,給出了機構組合方法與伸縮比計算公式。Deng[6]等給出了基于純鉸鏈連接設計單環展開/折疊機構的幾何方法。系統綜合了從5轉動副到8轉動副的單閉環空間機構構型，進而給出了一系列具有對稱運動度的單環展開/折疊機構。Lu[7]等以Hoekens機構為單元提出了一種新型的平面可展/收機構單元,該機構單元可在單一方向上改變其外形輪廓，在運動過程中其另一方向上的長度保持恒定,在此基礎上，通過在展收方向上的單元組合獲得了大型棱柱型展收機構。基于平面四桿機構的卡丹運動(Cardanic motion)，Shieh[8]提出了一個用于綜合平面和空間展開機構的系統方法。通過利用平面四桿機構(Cardanic linkages)連桿曲線為一條直線的特點，利用該機構建立了相應的可展機構單元，進而組合成了空間和平面可展機構。

文中將以平面四桿曲柄滑塊機構為基礎，根據機構軌跡輸出和函數輸出的特點[9]，分別對具有恒定截面的棱柱形可展機構和具有負泊松比的圓形可展機構進行設計。并對其進行機構建模和運動學仿真分析，通過動態仿真驗證其運動原理。

1　平面四桿曲柄滑塊機構輸出數學模型

1.1　軌跡輸出

平面四桿機構是結構最簡單、應用最廣的低副機構，曲柄滑塊機構作為四桿機構的一個類型，其機構模型如圖1所示。

圖1　平面四桿曲柄滑塊機構軌跡輸出模型

圖中，A點位于坐標原點處，AB和BC的桿長分別為l1和l2；P點為連桿BC上任意一點，BP的桿長為l3；滑道中心線與曲柄轉動中心的偏離距離為l4；BP與BC的夾角為α；x軸與AB桿夾角為θ1；連桿BC與x軸夾角為θ2。P點軌跡可以表示為xy平面上的一組點的集合，其解析式可寫為以θ1和θ2為變量的函數式：

xP=l1cosθ1+l3cos(α-θ2)

(1)

yP=l1sinθ1+l3sin(α-θ2)

(2)

當l1=l2=l3=l,l4=0且α=180°時，如圖2所示。

由式(1)和式(2)可得P點在x-y坐標系下的表達式為：

xP=lcosθ1-lcosθ2

(3)

yP=lsinθ1+lsinθ2

(4)

當-90°≤θ1≤90°時，由正弦定理可知θ2=θ1，則由式(3)和式(4)可得：

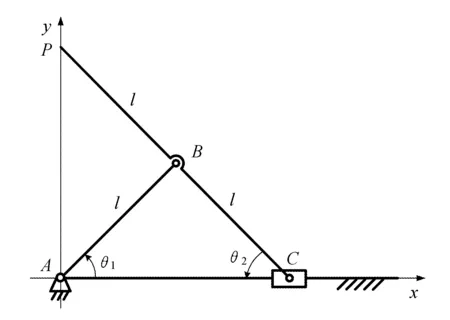
圖2　特定尺寸條件下四桿曲柄滑塊機構模型

當90°≤θ1≤270°時，由幾何關系可知θ2=180°-θ1，則由式(3)和式(4)可得：

xP=2lcosθ1

(7)

yP=2lsinθ1

(8)

將式(7)和式(8)整理可得

(9)

根據式(5)、式(6)和式(9)可以發現，當l1=l2=l3=l，l4=0且α=180°時，曲柄滑塊機構的連桿軌跡為一條直線和一個以2l為半徑的半圓構成的封閉曲線，如圖3所示。

圖3　軌跡輸出特點

1.2　函數輸出

四桿曲柄滑塊機構如圖4所示。

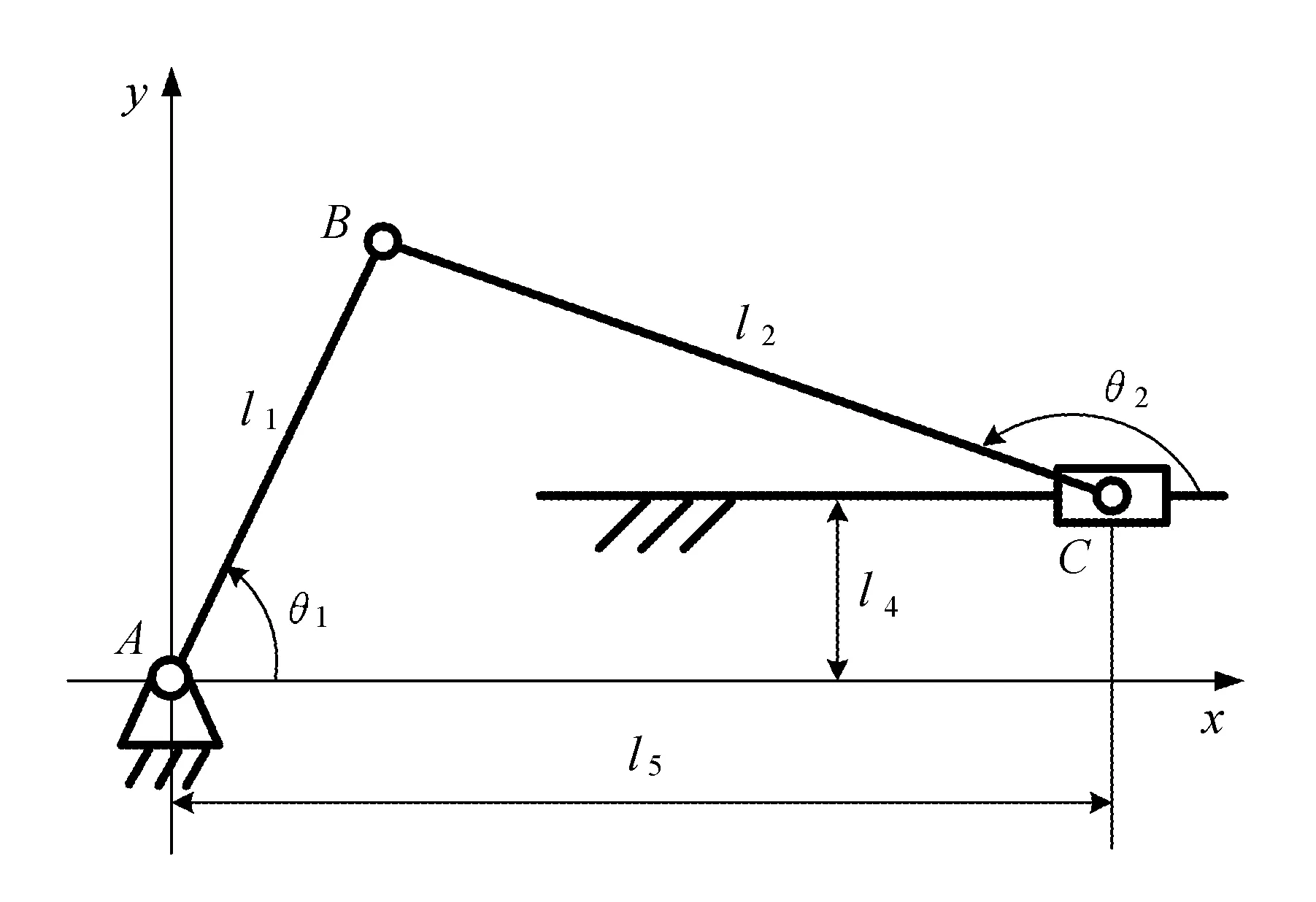
圖4　四桿曲柄滑塊機構

圖中，A點位于坐標原點處，AB和BC的桿長分別為l1和l2；滑道中心線與曲柄轉動中心的偏離距離為l4；θ1和θ2分別為桿AB和BC與x軸的夾角；l5為滑塊中心C點與A點在x軸方向上的距離。根據幾何關系，θ1與l5之間的函數關系為：

l5=l1cosθ1-l2cosθ2

(10)

同理，θ1與θ2之間的函數關系為：

l1sinθ1-l4=l2sin(180°-θ2)

(11)

整理可得：

(12)

當l4=0時，平面四桿曲柄滑塊機構函數輸出模型如圖5所示。

圖5　l4=0時平面四桿曲柄滑塊機構函數輸出模型

由式(12)可得,θ1與θ2之間的函數關系為：

(13)

(15)

2　具有恒定截面的棱柱展開機構

2.1　可展單元結構

通過1.1的運動分析，將圖2所示的能夠實現直線軌跡輸出的曲柄滑塊機構作為基本機構來設計,具有恒定截面可展機構單元,恒定截面可展機構單元結構如圖6所示。

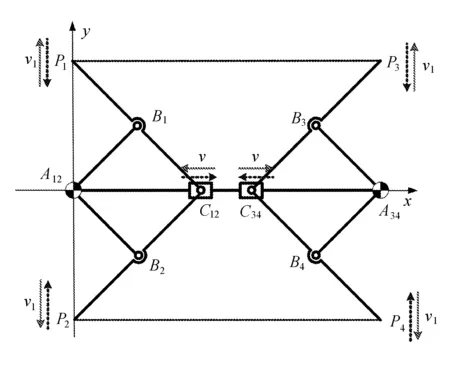
圖6　恒定截面可展機構單元簡圖

在圖6中，曲柄滑塊機構A12B1C12P1和A12B2C12P2通過共用絞點A12和滑塊C12來組成一對展收機構單元；同理，曲柄滑塊機構A34B3C34P3和A34B4C34P4通過共用絞點A34和滑塊C34來組成一對展收機構單元。將兩對機構滑動副共用的導軌組合在一起就構成了文中提出的具有恒定截面特點的可展機構單元，裝配形式如圖7所示。

圖7　恒定截面可展機構單元模型圖

當P1和P3的初始位置縱坐標相同時，可展單元在展收過程中P1、A12和P2始終保持在同一直線上，P2、A34和P4始終保持在同一直線上。可展單元包括12個絞點、2個滑動副和10個桿件,根據自由度計算公式可得機構單元的自由度為：

2.風險評估。風險評估是內部控制的首要前提，是在風險識別和預測的基礎上，采用定性或定量方法，對風險發生可能性和影響程度進行預計和估算，最終確定風險評級的過程。具體內容包括風險管理組織體系、風險識別和分類、風險評估、風險應對及風險監控與報告等。企業應全面梳理、識別和評估影響目標實現的相關風險，建立本企業風險清單或風險庫。針對不同風險，結合本企業的風險偏好和承受度，權衡利弊，按照成本效益原則制定完善相應的規避、降低、分擔或承受措施。通常情況下，內部風險可以進行有效防范和控制，外部風險主要采取規避。

F=3n-2PL=3×10-2×14=2

(16)

由于自由度為2，為保證展開和收攏的同步性，將兩個滑塊與同步帶固定后采用同一齒輪輸入動力來實現滑塊的同步反向運動，同時將單元的自由度降為1(展開與收攏過程見圖6)。

由圖6可知，單元收攏時的高度為圖2中兩根連桿BP厚度和一根曲柄AB厚度之和，而單元展開高度近似為4l。

2.2　可展機構單元組合連接

以圖6所示的可展機構為基本單元，通過組合就可以構成具有恒定截面的棱柱形可展機構，恒定截面三棱柱可展機構展開過程如圖8所示。

圖8(a)和(b)分別為三棱柱可展機構收攏狀態下的主視圖和俯視圖。圖8(c)～(f)為具有恒定截面三棱柱可展機構的展開過程。從圖中可以看出，在機構展開過程中其橫截面(圖8中三角形框架)始終保持不變。

恒定截面四棱柱可展機構展開過程如圖9所示。

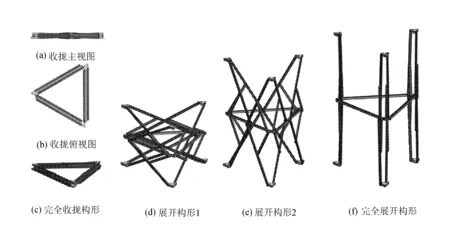
圖8恒定截面三棱柱可展機構展開過程

圖9　恒定截面四棱柱可展機構展開過程

圖9(a)和(b)分別為兩段四棱柱可展機構收攏狀態下的主視圖和俯視圖。圖9(c)～(g)為具有恒定截面四棱柱可展機構的展開過程。從圖中可以看出，在機構展開過程中其橫截面(圖9中四邊形框架)始終保持不變。基于文獻[7]的研究成果，為保證圖9中上、下兩段可展機構的同步展收，文中采用在上、下兩段可展機構的連接絞點添加齒輪副實現動力傳遞。

3　負泊松比可展機構

3.1　負泊松比可展單元結構

通過1.2的運動分析，將圖5所示的曲柄滑塊機構作為基本機構來設計,具有負泊松比可展機構單元如圖10所示。

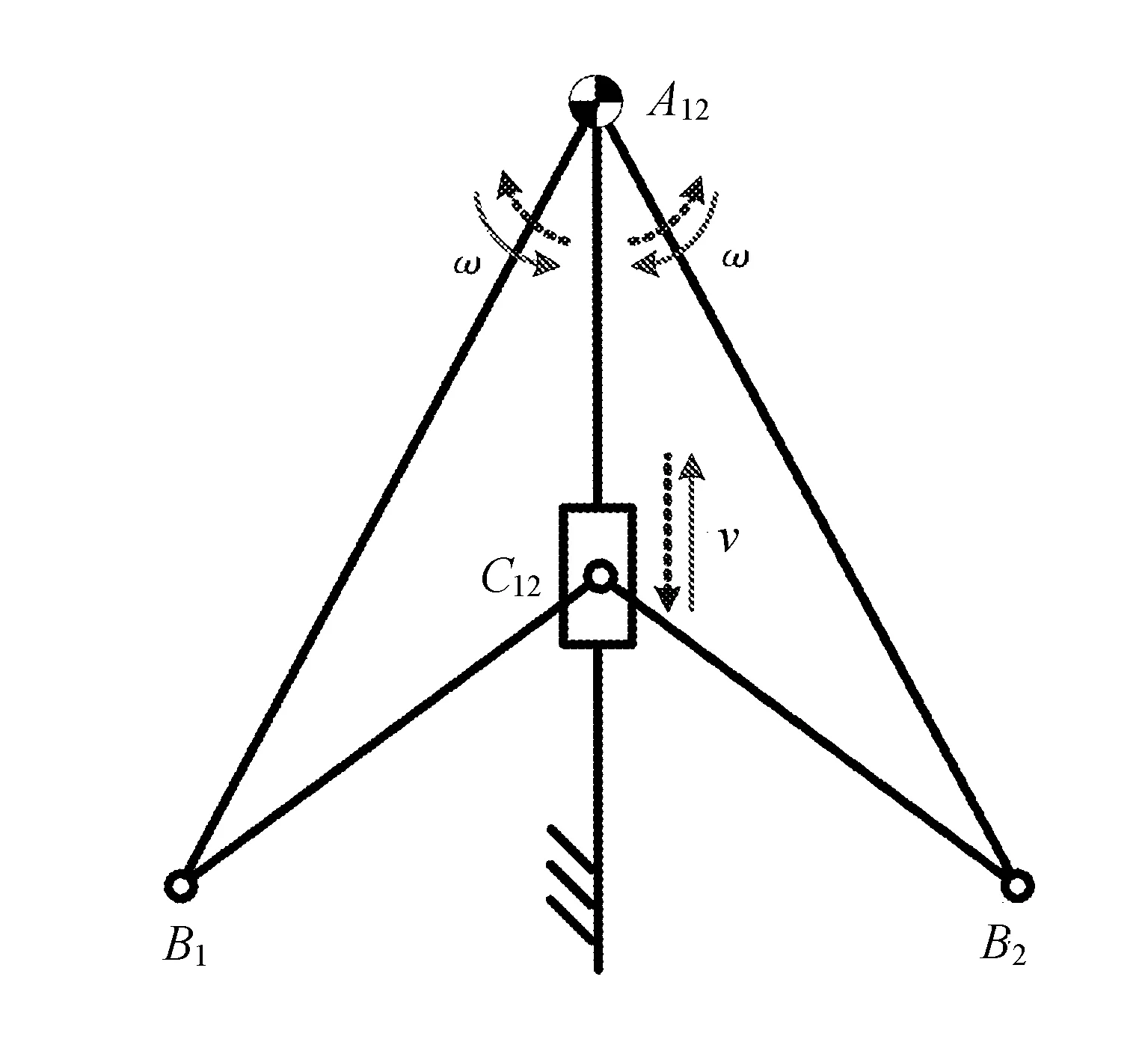
圖10　負泊松比可展機構單元簡圖

在圖10中，曲柄滑塊機構A12B1C12和A12B2C12通過共用絞點A12和滑塊C12來組成一對展收機構單元，裝配形式如圖11所示。

圖11　負泊松比可展機構單元模型圖

可展單元包括6個絞點、1個滑動副和5個桿件,根據自由度計算公式可得機構單元的自由度為：

F=3n-2PL=3×5-2×7=1

(17)

由于自由度為1，可展單元需用一個氣缸推動滑塊實現機構的展開與收攏。

基于圖11所示的可展機構單元，文中設計了l1和l2的長度分別為310 mm和490 mm ，3×3單元布局的平板式可展機構。

負泊松比可展機構展收構態如圖12所示。

圖12負泊松比可展機構展收構態

圖12(a)和(b)分別是該機構的收攏和展開狀態時的俯視圖。從圖中可以看出，機構在展開收攏過程中，其尺寸在兩個方向上同時增加或減少(由于這種現象與材料學中的負泊松比材料的拉伸膨脹類似，文中定義該機構為具有負泊松比特點的可展機構)。對于可展機構,伸縮比是一個重要的性能指標，我們可以通過對l1和l2長度的調整來實現機構伸縮比和負泊松比的控制。

3.2　圓形可展機構

由于圓形展開面在展開過程中隨著半徑的增大，展開面的周長也在增大，因此，要求可展機構在展開過程中需要具有負泊松比特點，而傳統的可展單元很難實現這一要求。文中以圖11所示的可展機構為基本單元，通過組合構成了可以實現圓形展開面要求的負泊松比可展機構，如圖13所示。

圖13(a)～(d)為該可展機構的展開過程。圖13(e)和(f)分別為可展機構收攏狀態和完全展開狀態下的俯視圖。從圖13(f)中可以看出，在機構展開后可基本實現近似的圓形展開。

4　結　語

1)給出了通過組合四個曲柄滑塊機構來構成具有恒定截面的平面可展機構單元的方法。通過提出的可展機構單元的進一步組合，設計出了具有恒定截面的棱柱可展機構。該可展機構可保證展開過程中保持底座長度不變的要求，并具有較大的伸縮比。此外，通過對棱柱可展機構單元的組合可在其展收方向上形成大型棱柱形可展機構。

2)根據曲柄滑塊機構函數輸出特點，給出了通過組合兩個曲柄滑塊機構來構成具有負泊松比特性的平面可展機構單元的方法。通過提出的可展機構單元的進一步組合，設計出了具有圓形展開面的可展機構。并對該可展機構進行了設計和仿真，通過仿真結果可以看出，該結構能夠基本實現大尺度圓形展開面的設計要求。

3)文中僅僅基于曲柄滑塊機構對兩種可展單元進行了初步的結構設計，沒有進行相應的運動學分析、展開面強度分析、靜力學性能分析和自振頻率特性分析。因此在下一步的工作中，將針對以上問題進行進一步分析與研究，進而給出兩種可展單元結構的最優參數。

圖13圓形可展機構展開過程

參考文獻：

[1]A Das, M W Obal. Revolutionary satellite structural systems technology: avision for the future[J]. IEEE Aerospace Conference，Snowmass at Aspen, USA,1998,21(28)：57-67.

[2]劉榮強,田大可,鄧宗全.空間可展開天線結構的研究現狀與展望[J].機械設計,2010,27(9):1-9.

[3]廖啟征,李端玲.單層及多層平面圖形放縮機構的構造方法[J].機械工程學報,2008,44(6):43-48.

[4]李端玲,張忠海,于振.球面剪叉可展機構的運動特性分析[J].機械工程學報,2013,49(13):1-7.

[5]楊毅,丁希侖.四棱錐單元平板式可展開收攏機構的運動特性分析[J].航空學報,2010,31(6):1257-1265.

[6]Z Q Deng, H L Huang, B Li, et al. Synthesis of deployable/Foldable single loop mechanisms with revolute joints[J]. ASME Journal of Mechanisms and Robotics,2011,3(3):031006.1-031006.12.

[7]S N Lu, D Zlatanov, X L Ding, et al. A new family of deployable mechanisms based on the hoekens linkage[J]. Mechanism and Machine Theory,2014,73:130-153.

[8]W B Shieh. Design of the deployable mechanisms based on the cardanic motion of planar four-Bar linkage[J]. Mechanisms and Robotics Conference, V05AT08A061, Buffalo, New York, USA,2014,38:17-20.

[9]蒼鵬，劉文瑞，孫建偉.平面連桿機構軌跡輸出的小波分析[J].長春工業大學學報，2015,36(4):433-437.