無限導流水平井試井分析模型的研究

(大慶油田有限責任公司測試技術服務分公司　黑龍江　大慶　163453)

0　引　言

1950年以后，裂縫井內不穩定滲流壓力的研究逐漸進入研究者的視線。1972年Cady與Ramey利用MDH法和Muskat校正法進行了試井分析，此后，Gringarten[1]、Cinco-Ley[2]等人分別求解了無限導流裂縫及有限導流裂縫的不穩定壓力，經過Bordet、Harrington、D.Tiab[3]等人的研究，逐漸形成了一種利用壓力及壓力導數對無因次時間曲線進行快速獲取試井參數的方法，即TDS試井解釋技術。在TDS方法中，利用繪制的壓力與壓力導數對時間的對數曲線，對相關參數如滲透率、裂縫半長、表皮系數以及孔隙度進行求解。TDS方法利用相關參數計算公式與繪制無因次典型曲線斜率間的關系，對油藏參數進行求解。油氣在裂縫中的流動模型因裂縫特征的區別可劃分為三類，有限導流模型、無限導流模型及均勻流量模型，本文主要采用無限導流模型，對水平井壓裂技術中的試井模型進行建立和求解。

水平井壓裂技術具有泄油面積較大、縱向的掃油距離較遠、易于開采薄層、連通裂縫更廣、成本較低等優點，因此其在油藏開發中扮演著越來越重要的角色。水平井壓裂技術對油藏監測、管理及評價技術的要求較高，因此試井工作[4]的作用尤為突出。本文利用無限導流裂縫模型對壓裂水平井的試井模型進行求解，分析壓力及壓力導數曲線特性以及不同裂縫參數對其的影響規律，以期為水平井壓裂的試井工作提供理論借鑒。

1　水平井壓裂無限導流多裂縫模型

1.1　無限導流裂縫模型

若垂直裂縫全部切割直井，直徑位于垂直裂縫的中心地帶，則無因次壓降可描述為：

(1)

式(1)中，pwD為無因次壓力，其表達式可寫為：

(2)

式(2)中，k為地層滲透率，μm2；h為油層厚度，m；pi為原始地層壓力，MPa；pwf為裂縫壓力，MPa；q為該井產量，m3/d；μ為流體粘度，mPa·s。

txfD為考慮裂縫半長無因次時間，其表達式可寫為：

(3)

式(3)中，tD為無因次時間；rw為裂縫邊界半徑，m；xf為裂縫半長，m；Φ為孔隙度；ct為壓縮系數，1/MPa；t為時間，h。

無限導流裂縫模型將裂縫導流能力認為無限大，流體在裂縫中流動過程中壓降為零，且裂縫寬度假設為無限小。在式(1)中，將xD=0.372[5]帶入其中可計算得出均質無限大油藏無限導流裂縫的井底無因次壓降。將式(1)中無因次壓力pwD對無因次時間txfD進行求導得：

(4)

當xD=0時，且在較短的時間內，即txfD<1時，式(4)可轉化為：

(5)

在無限導流裂縫模型中，當無因次時間txfD處于0.02與0.2之間，即在線性流與徑向流動區域間出現“雙徑向流”區間，在此區間內，無因次壓力對時間的導數可表示為：

(6)

即

(7)

(txfD)LBRi=0.01

(8)

由式(3)和式(7)可得出

(9)

式(9)中，tLBRi為流動段分段時間；xf為裂縫半長，m；Φ為孔隙度；ct為壓縮系數，1/MPa；k為地層滲透率，μm2；μ為流體粘度，mPa·s。

進而由式(6)與(8)求解地層滲透率：

(10)

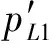
由式(9)與式(10)求解得出裂縫半長為：

(11)

1.2　無限導流多裂縫模型

利用無限導流模型對水平井壓裂多裂縫進行分析時，對均質無限大油藏中水平井多裂縫進行假設：

首先，分析對象為均質油藏，油層在x、y方向為無限大且頂底邊界均認為不滲透，油層在x、y方向的滲透率不同；第二，油層的邊界與水平井筒平行，裂縫長度為L，其處于油層中Z處，裂縫m位于xwi,ywi,zw處；第三，任意半長的多裂縫與井筒相垂直，裂縫間距任意且認為寬度無限小；第四，流入井筒中的流體認為全部來自于裂縫，其它渠道流入的流量可忽略；第五，不考慮重力因素影響；第六，忽略流體由裂縫進入井筒瞬間產生的壓降；最后，將流體認為不可壓縮流體，其粘度即壓縮系數不變。

利用格林函數[6]

(12)

則某特定流量源周邊的壓力分布表達式為：

(13)

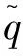
(14)

式(14)中，xD為源周邊x方向坐標，tD為無因次時間。

Sy定義為y方向源，其表達式為：

(15)

式(15)中，yD為源周邊y方向坐標，ywD為源點Y坐標，tD為無因次時間。

在無限導流模型中，長直狀導流裂縫與X軸平行，多條平行裂縫與Y軸垂直，則格林函數可用Sx、Sy表示：

(16)

式(16)中，ywi為裂縫y坐標；t為時間，s；q為排液量。

無因次壓力表達式為：

(17)

將xD=0.372代入，即可得到無限導流模型的井底不穩定壓力響應。

2　無限導流多裂縫模型流動特性及影響參數分析

2.1　流動特性分析

對模型進行求解，根據結果繪制無限導流模型描述下的水平井壓裂的井底壓力與壓力導數的變化曲線，裂縫條數為3，如圖1所示，在均質無限大的油藏中，無限導流裂縫的壓力相應曲線可劃分為5個階段，其中圖中實線表示為壓力導數對時間的雙對數理論曲線圖，虛線表示壓力對時間的雙對數理論曲線圖。

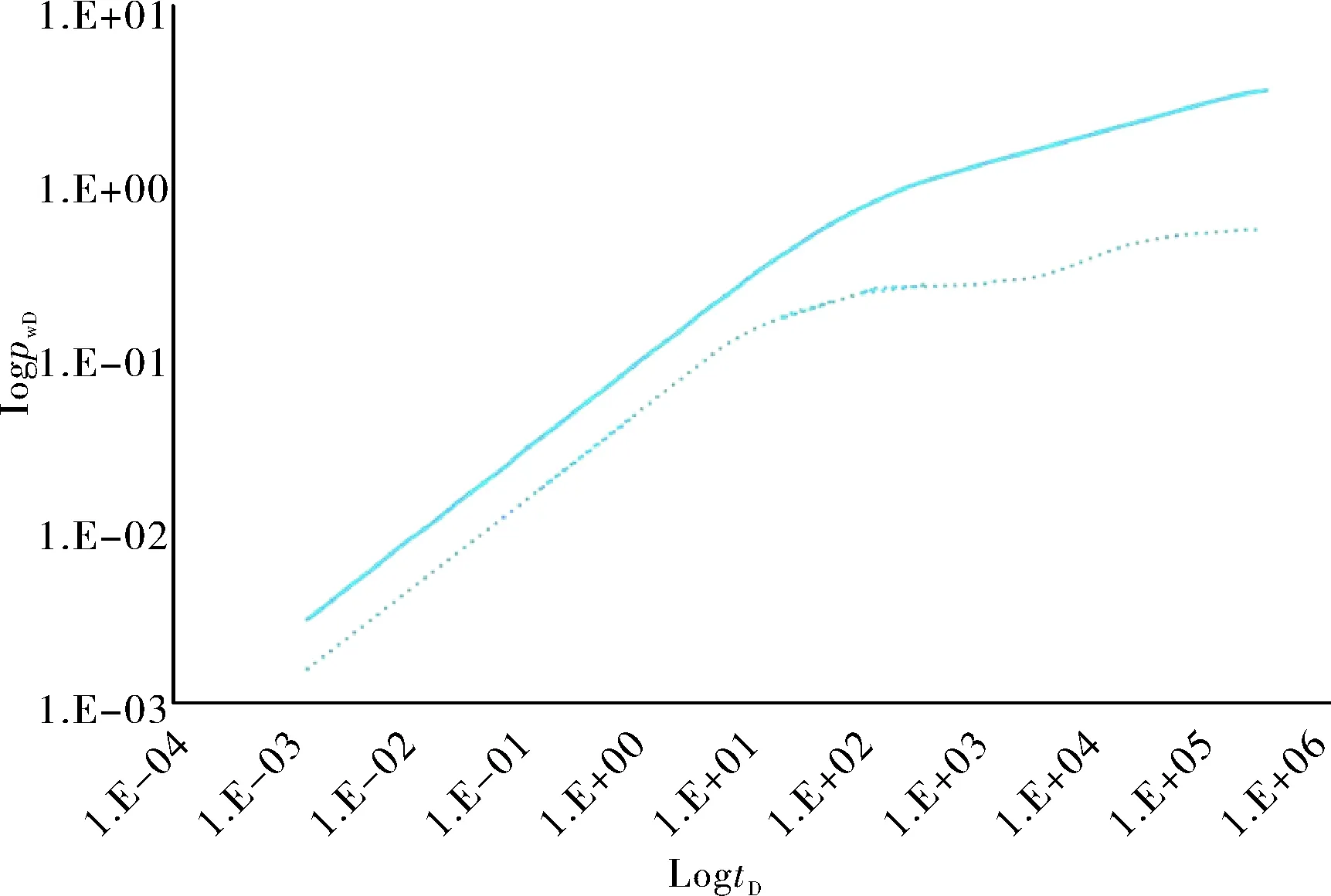
圖1　無限導流模型水平井壓裂井底壓力曲線圖

第一階段，為起始段線性流階段，在此階段，裂縫周邊地層中的流體沿垂直裂縫的方向流入裂縫內，在此過程中，不同裂縫間互不干擾，在曲線圖中壓力與壓力導數曲線為直線，斜率為0.5。

第二階段，為第一雙徑向流階段，此階段為流體由沿裂縫垂直裂縫的方向流動變化至平行于裂縫方向流動的中間階段，曲線圖中此階段為斜率0.36的直線。

第三階段，為早期徑向流階段，在此階段，流體流動區域逐漸接近裂縫周邊，壓力影響范圍呈類圓形區域，流體由裂縫周邊進入裂縫的流動方式為擬徑向流，此時不同裂縫間仍不存在相互干擾，此階段在壓力導數曲線中為一水平直線。

第四階段，為雙徑向流階段，在此階段，由于流體流動區域的不斷拓展，裂縫周邊地層中的流體以擬徑向流流入裂縫，距離裂縫較遠處的流體同時向近裂縫地帶流動，在此階段中，不同裂縫間會出現干擾，其在壓力導數曲線圖中為斜率0.36的直線段。

第五階段，為系統擬徑向流階段。在此階段，流體的流動區域不斷拓展，遠縫地帶的流體向水平井段流動，其在曲線圖中為恒值為0.5的水平直線。

2.2　裂縫參數對壓力動態曲線的影響

1)多裂縫間距的影響規律

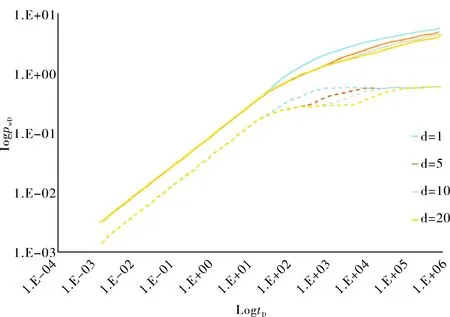
圖2　裂縫間距對水平井壓裂壓力動態曲線的影響圖

圖2為不同無因次裂縫間距下壓力與壓力導數對時間的雙對數變化曲線圖，其中實線為不同無因次裂縫間距下壓力導數對時間的雙對數變化曲線，虛線為不同無因次裂縫間距下壓力對時間的雙對數變化曲線。由圖2可見，當無因次裂縫間距增大、其他參數恒定時，早期徑向流階段所占時間比例增大，因而雙徑向流階段與系統擬徑向流階段產生的時間受到延遲。產生這種現象的主要原因是，隨無因次裂縫間距增大，不同裂縫間產生的干擾將不斷減小，因而雙徑向流階段產生的時間較晚。

2)裂縫數量的影響規律

圖3為裂縫數量對井底壓力動態曲線的影響圖，從圖3中可見，在其他條件恒定時，隨著裂縫數量由1增長至4，壓力導數曲線整體呈降低趨勢。產生這種現象的原因在于，當裂縫數量變大時，水平井井筒周圍裂縫數量增多，滲透性增強，因此初期井底壓力隨時間的變化較為平緩，即數量越大的壓力導數曲線整體下移。

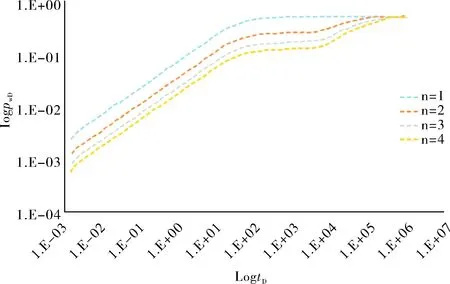
圖3　裂縫數量對水平井壓裂井底壓力動態曲線的影響規律圖

除此之外，裂縫數量的改變對系統擬徑向流階段與雙徑向流階段的影響較大，而對初期線性流階段和早期徑向流階段的規律影響較小。隨著裂縫數量增大，不同裂縫間干擾效應增強，因此雙徑向流階段持續時間隨裂縫數量的增多而增長，而系統擬徑向流動階段產生時間較晚。

3)裂縫半長的影響規律

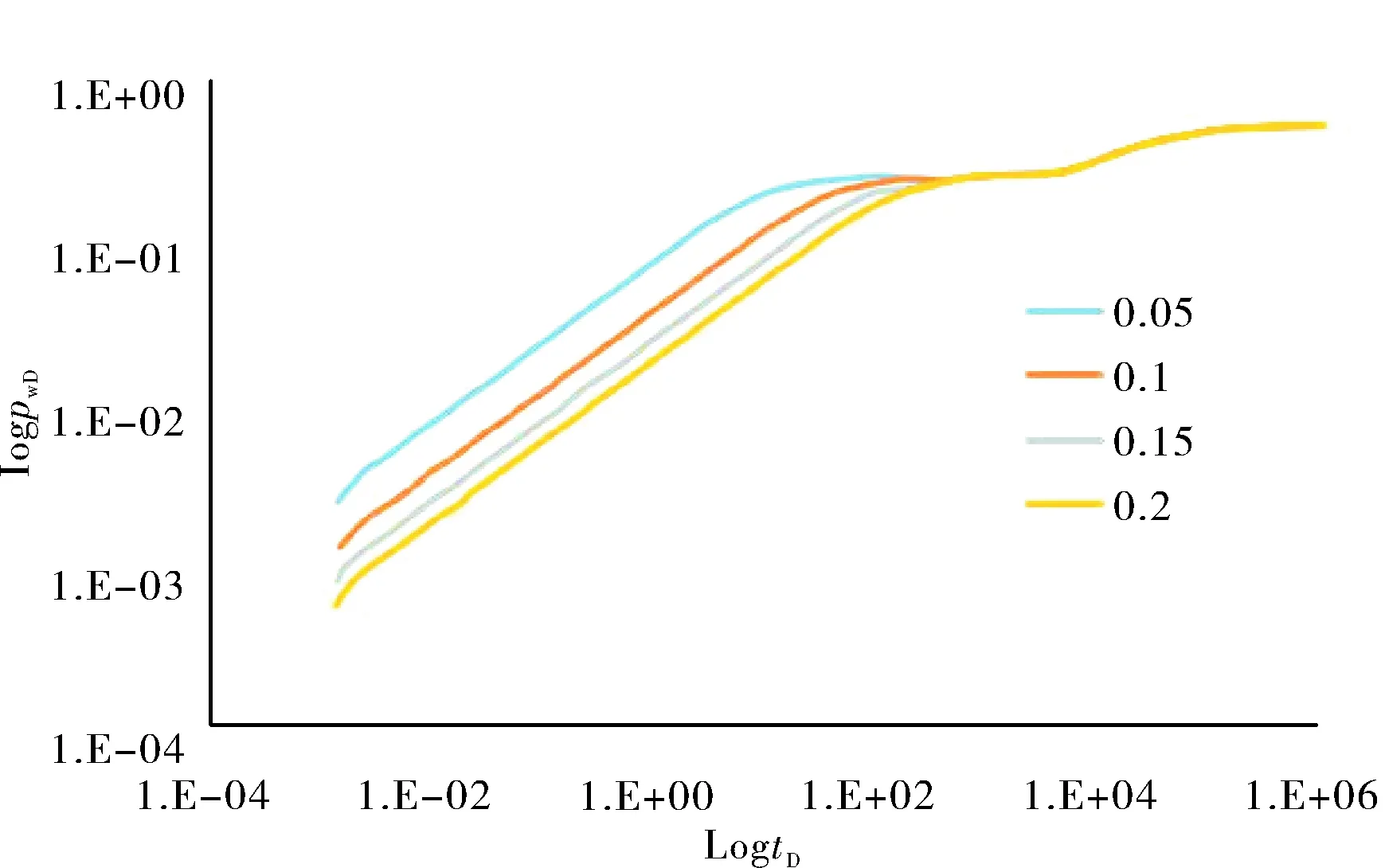
圖4　裂縫半長對水平井壓裂井底壓力動態曲線的影響規律圖

圖4為裂縫半長變化對壓力導數對時間雙對數曲線的影響規律圖，由圖4可見，在其他條件恒定時，無因次裂縫半長由0.05增長至0.2的過程中，井底壓力曲線的初期階段下移。隨著裂縫半長的增大，當固定井生產能力不變時，井底壓降降低，因此井底壓力曲線隨裂縫半長的增加而降低。裂縫半長增大對雙徑向流與系統擬徑向流階段不產生影響，而使得壓力導數曲線的初期線性階段與早期徑向流階段持續時間減小。

3　結　論

將無限導流裂縫模型與水平井壓裂相結合，利用無限導流模型建立了水平井壓裂多裂縫的壓力及壓力導數隨時間變化曲線，根據曲線可計算滲透率、裂縫參數等數據。在所得曲線基礎上，對5個不同的流動階段進行了特性分析，著重討論了裂縫間距、裂縫數量及裂縫半長對壓力變化的影響，為水平井壓裂試井工作提供了相關理論借鑒。

[1] GRINGARTEN A C, RAMEY H J. The use of source and Green’s functions in solving unsteady-flow problems in reservoirs[J]. Society of Petroleum Engineers Journal, 1973, 13(05): 285-296.

[2] CINCO L, SAMANIEGO V, DOMINGUEZ A. Transient pressure behavior for a well with a finite-conductivity vertical fracture[J]. Society of Petroleum Engineers Journal, 1978, 18(04): 253-264.

[3] TIAB D. Direct type-curve synthesis of pressure transient tests[C]//Low Permeability Reservoirs Symposium. Society of Petroleum Engineers, 1989.

[4] 王博, 楊恒遠, 王昊,等. 致密氣井修正等時試井分析新方法[J]. 長江大學學報(自科版), 2016, 13(11):54-59.

[5] GRINGARTEN A C, RAMEY Jr H J. Unsteady-state pressure distributions created by a well with a single horizontal fracture, partial penetration, or restricted entry[J]. Society of petroleum engineers journal, 1974, 14(04): 413-426.

[6] 邊鳳曉. 壓裂水平井試井分析模型應用研究[D]. 西安：西安石油大學,2012.