基于窗口Hough變換與閾值分割的矩形識(shí)別算法①

賀 輝, 閆 明, 黃 靜

(北京師范大學(xué)珠海分校 信息技術(shù)學(xué)院,珠海 519087)

矩形結(jié)構(gòu)的識(shí)別被廣泛應(yīng)用在各個(gè)領(lǐng)域,例如低溫電子顯微鏡下對(duì)矩形和圓形微粒的自動(dòng)檢測(cè); 航拍圖片中對(duì)矩形結(jié)構(gòu)(例如車輛、建筑物)的自動(dòng)或半自動(dòng)檢測(cè); 或者檢測(cè)圖像或錄像里的車牌辨識(shí)等等. 目前文獻(xiàn)論述的大多數(shù)矩形檢測(cè)方法是基于原始邊緣和直線的檢測(cè)[1-3]以及基于圖像閾值分割檢測(cè)矩形[4-8]. 例如Lagunovsky和Ablameyko提出了基于原始直線的矩形檢測(cè)技術(shù)[1]. 首先,提取出原始直線,將這些直線分組聚合為線段. 對(duì)比其長(zhǎng)度和方向來(lái)檢測(cè)出四邊形,再進(jìn)一步近似為矩形. Lin和Nevatia提出了在航拍圖像中檢測(cè)矩形和平行四邊形的技術(shù)[2]. 他們的技術(shù)基于線檢測(cè),之后選擇某些在某些值范圍內(nèi)的線段(取決于建筑物的最大和最小尺寸). 在給定的線段中搜索反平行線,從而定義一個(gè)搜索區(qū)域,再搜索矩形的余下兩條邊.Jung和Schramm提出了一種使用一個(gè)環(huán)形滑動(dòng)窗口在圖像中進(jìn)行逐像素掃描,對(duì)當(dāng)前環(huán)形窗口內(nèi)的圖像求Hough變換,通過(guò)檢驗(yàn)Hough空間內(nèi)的峰值的特性,來(lái)判斷當(dāng)前滑動(dòng)環(huán)的圓心是否落在矩形的中心點(diǎn)[3]. 這種方法可以有效精確地檢測(cè)出任意矩形,但是逐行掃描的方式會(huì)導(dǎo)致大量像素點(diǎn)被重復(fù)計(jì)算,算法效率低.Mahnaz Shafii和Maher Sid-Ahmed在近年來(lái)的研究中提出了一種基于圖像中的平行軸邊界框的最小面積來(lái)對(duì)文檔中的結(jié)構(gòu)進(jìn)行傾斜檢測(cè)和矯正. 通過(guò)使用最小邊界框的區(qū)域標(biāo)準(zhǔn)來(lái)增強(qiáng)垂直輪廓和平行輪廓. 這種方法在多種傾斜角度中都可以有效地匹配[4]. 而基于閾值分割的方法對(duì)輸入圖像目標(biāo)和背景反差要求較高,容易受到噪聲的干擾而不易準(zhǔn)確的檢測(cè)到目標(biāo)矩形[9-11].

本文面向銀行票據(jù)自動(dòng)裁剪應(yīng)用需求,結(jié)合了基于直線的檢測(cè)和基于圖像閾值分割的兩種策略的優(yōu)點(diǎn)以及在特定環(huán)境下的局限性,提出了一種基于窗口霍夫變換與閾值分割的圖像中矩形的自動(dòng)識(shí)別策略： 對(duì)全局圖像的Hough Space峰值進(jìn)行匹配,將匹配的結(jié)果與對(duì)圖像閾值分割的結(jié)果做擬合,從而得到票據(jù)的目標(biāo)區(qū)域. 具有如下特點(diǎn)： 1) 能有效區(qū)分非目標(biāo)區(qū)域的噪聲結(jié)構(gòu)干擾; 2) 無(wú)須設(shè)定閾值; 3) 算法性能優(yōu)越,匹配結(jié)果快速準(zhǔn)確.

1 算法原理

1.1 Hough變換原理(HT)

HT是利用圖像的全局特征將圖像的形態(tài)學(xué)信息做變換與統(tǒng)計(jì)的方法,HT用來(lái)檢測(cè)一個(gè)圖像的線性結(jié)構(gòu)是很有效的. J.Princen等提出了對(duì)Hough變換的正式的數(shù)學(xué)定義. 廣義的霍夫變換(Hough transform)可以表示為通過(guò)對(duì)目標(biāo)形狀的量化所得到的核函數(shù)(Kernel Function)在關(guān)于數(shù)據(jù)點(diǎn)集合之內(nèi)的積分. 其中,Kernel Function為目標(biāo)的形狀和量化參數(shù)空間之間的轉(zhuǎn)化關(guān)系[12]. Duda和Hart[13]的研究表明任何線在xy平面內(nèi)都能被描述成. 其中,ρ是垂直距離,θ是直線的垂直角度. 霍夫變換將一個(gè)二維圖像的邊緣點(diǎn)集合使用二維函數(shù)轉(zhuǎn)換為滿足的線段的邊緣點(diǎn)集合. 而在實(shí)際應(yīng)用中,傾角θ和垂直距離ρ可以被量化,得到一個(gè)數(shù)組,這個(gè)數(shù)組的峰值可以被用來(lái)檢測(cè)邊緣點(diǎn)聚合成的線段[13].

由于在霍夫空間的線段峰值特性明顯,因此基于霍夫空間的基線模式的檢測(cè)被廣泛應(yīng)用. Abdelhak所提出的基于隨機(jī)霍夫變換的技術(shù)用于對(duì)阿拉伯語(yǔ)文件的傾斜校正和基線檢測(cè)[14]. 通過(guò)計(jì)算文本行中較低基線的斜率來(lái)識(shí)別和矯正文檔的傾角. Trupti的研究中也將霍夫變換應(yīng)用于手寫(xiě)梵文文檔的傾斜檢測(cè)和矯正,通過(guò)提取文檔的每個(gè)詞,對(duì)每個(gè)詞語(yǔ)單元做霍夫變換來(lái)檢測(cè)歪斜[4]. 我們?cè)缙诘难芯恳餐ㄟ^(guò)霍夫空間的基線檢測(cè)技術(shù)來(lái)對(duì)銀行票據(jù)進(jìn)行預(yù)處理[15].

在圖像中識(shí)別矩形包含多個(gè)對(duì)象,我們需要在給定的霍夫空間中檢測(cè)出能夠識(shí)別出矩形特征的模式.因此,我們記錄了一些矩形所包含的特定幾何聯(lián)系,可以用來(lái)直接在霍夫空間中做檢測(cè).

1.2 在Hough Space里的矩形特征模式

圖1 處在笛卡爾坐標(biāo)系的矩形

圖2 對(duì)矩形做Hough變換的Hough space

2) 屬于同一對(duì)峰值點(diǎn)的兩個(gè)峰值高度是相等的,對(duì)應(yīng)到各自的線段的長(zhǎng)度. 例如和.

若在當(dāng)前圖像中有其他結(jié)構(gòu),這些邊緣會(huì)和干擾信息和其他結(jié)構(gòu)相關(guān)聯(lián),也許也會(huì)匹配這些幾何關(guān)系.因此,對(duì)干擾信息的去除也是不可缺少的步驟.

1.3 構(gòu)建并分析峰值點(diǎn)集合

接下來(lái)是通過(guò)在所得的離散化Hough空間里尋找峰值來(lái)檢測(cè)線段. 由于表示滿足線性方程的邊緣點(diǎn)的數(shù)量,因此找到霍夫圖像的峰值的簡(jiǎn)單方法是提取滿足的所有點(diǎn)(即檢索像素點(diǎn)大于等于TC的所有直線),得到一個(gè)離散點(diǎn)聚合. 但是,噪聲和其他結(jié)構(gòu)會(huì)降低這種估計(jì)峰值的精度[7]. 為此,使用butterfly模式去分析峰值附近區(qū)域可以有效地增強(qiáng)區(qū)域擬合度[6].Butterfly模式在此不做太多解釋,此方面,Furukawa和Shinagawa提出了一個(gè)簡(jiǎn)化版本的butterfly計(jì)算用來(lái)增強(qiáng)霍夫圖像[7]. 對(duì)于給定的圖像,對(duì)應(yīng)的增強(qiáng)公式為：

其中h和w表示增強(qiáng)過(guò)的矩形區(qū)域的長(zhǎng)和高. 由于ρ和θ已經(jīng)被量化,所以通過(guò)矩形遮罩的卷積來(lái)求上式的積分. 最終,將滿足的增強(qiáng)圖像的局部最大值存儲(chǔ)為峰值.

上式中,Tθ是最小容錯(cuò)角度閾值,TL是最小容錯(cuò)歸一化閾值所映射的原圖關(guān)系是線段Hi和Hj互相平行,所映射的原圖關(guān)系為線段Hi和Hj長(zhǎng)度相等. 而所找到的即為具有平行特征的線段.

2 關(guān)鍵算法實(shí)現(xiàn)

2.1 Canny算子[17]對(duì)票據(jù)做邊緣檢測(cè)預(yù)處理

由于光照的干擾,將彩色票據(jù)圖像轉(zhuǎn)化為灰度圖像會(huì)有可能丟失邊緣細(xì)節(jié)特征,考慮到接下來(lái)的工作需要對(duì)圖像做閾值分割,所以本文直接對(duì)彩色圖像的RGB三通道進(jìn)行處理.

2.2 對(duì)邊緣圖像做Hough變換

在M*N目標(biāo)圖像中,將ρ離散化為p*ρ個(gè)參數(shù)空間,將θ離散化為K*θ個(gè)參數(shù)空間. 對(duì)于p和K的選取,Furukawa和Shinagawa所提出的方法具有借鑒意義,對(duì)于一個(gè)M*N圖像來(lái)說(shuō),計(jì)算出的霍夫圖像長(zhǎng)為4M/3,寬為4N/3. 在這個(gè)情況下,可以設(shè)定M=N=Dmax,即可得離散步長(zhǎng)對(duì)于在本例的票據(jù)實(shí)驗(yàn)用例中,為了簡(jiǎn)化運(yùn)算,我們?nèi)=180,步長(zhǎng)step = 1. 因此計(jì)算得到的Hough變換結(jié)果圖像寬度和高度分別為和180.

2.3 構(gòu)建并分析峰值點(diǎn)集合檢測(cè)矩形

在實(shí)際應(yīng)用中,由于銀行票據(jù)通常具有固定不變的長(zhǎng)寬比,該約束條件可以用來(lái)在當(dāng)前所找到的兩對(duì)的集合中再一次搜尋,尋找符合以下條件的Pair,即進(jìn)一步完成了對(duì)目標(biāo)區(qū)域的約束：

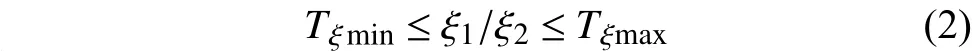
2.4 對(duì)圖像做閾值分割

此處采用我們?cè)缜疤岢龅淖赃m應(yīng)直方圖閾值二值化的目標(biāo)分割算法[15]. 分割結(jié)果往往包含噪聲,如孤立點(diǎn)噪聲或呈塊狀的噪聲,可以分別通過(guò)中值濾波和對(duì)形態(tài)學(xué)操作來(lái)消除.

2.5 將分割結(jié)果與霍夫變換的矩形做擬合修正

最后,我們得到了一個(gè)存儲(chǔ)圖像矩形信息的集合List＜R>和一個(gè)二值化的圖像. 遍歷List＜R>的元素,將每一個(gè)矩形元素映射到二值化圖像中,對(duì)目標(biāo)矩形區(qū)域內(nèi)的像素做采樣,記錄矩形元素和二值圖像的擬合值,選擇最大值的矩形元素. 此矩形即為目標(biāo)矩形.

3 算法測(cè)試

為了驗(yàn)證本文所提出的方案的有效性,本文面向銀行票據(jù)自動(dòng)裁剪需求,選取了50組真實(shí)拍攝銀行票據(jù)圖像進(jìn)行識(shí)別率測(cè)試. 銀行票據(jù)具有較為完整的矩形結(jié)構(gòu),但是真實(shí)拍攝的銀行票據(jù)圖像存在的多種自然光照不均和拍攝角度造成的干擾對(duì)票據(jù)的準(zhǔn)確識(shí)別帶來(lái)了難度.

測(cè)試中,本文將使用我們?cè)缙诘难芯拷Y(jié)果自適應(yīng)閾值分割方法(即對(duì)糾偏圖像進(jìn)行自適應(yīng)二值分割,確定裁剪框的方法)[15]和本文所提出的方法所測(cè)試的結(jié)果進(jìn)行識(shí)別率的比對(duì).

3.1 測(cè)試數(shù)據(jù)

本研究工作的測(cè)試數(shù)據(jù)為高清攝像機(jī)采集的照片圖像,分為2種分辨率,分別是2592*1944和1600*1200.本文將給出其中的2個(gè)典型數(shù)據(jù),如圖3所示. 其中,圖3(a)的票據(jù)整體呈矩形,但是四條邊均存在褶皺,圖3(b)里包含一張黃色的小矩形作為匹配的非目標(biāo)區(qū)域. 兩組數(shù)據(jù)的背景和票據(jù)的灰度差異并不能完全地拉開(kāi),這無(wú)疑降低了閾值分割方法的匹配度.

圖3 待測(cè)試的票據(jù)圖像

3.2 實(shí)驗(yàn)結(jié)果及分析

使用自適應(yīng)閾值分割裁剪的結(jié)果如圖4所示. 實(shí)驗(yàn)結(jié)果表明,在沒(méi)有其他矩形干擾情況下,該方案能有效準(zhǔn)確地識(shí)別出票據(jù),并且不會(huì)留下明顯的黑邊,如圖4(a)所示. 然而,如果背景和票據(jù)的灰度反差降低,會(huì)導(dǎo)致在二值圖像內(nèi)仍然存在除了目標(biāo)區(qū)域之外的背景區(qū)域未被分割. 易將包括亮背景區(qū)域的矩形當(dāng)成目標(biāo)矩形,從而導(dǎo)致裁剪結(jié)果不當(dāng),如圖4(b)所示.

本文方法裁剪結(jié)果如圖5所示. 結(jié)果表明,在存在嚴(yán)重背景干擾情況下,此裁剪結(jié)果仍能有效地識(shí)別出票據(jù). 這個(gè)結(jié)果主要是得益于Hough變換帶來(lái)的所有可能性的矩形匹配.

由對(duì)比結(jié)果可以看出,自適應(yīng)二值化分割算法一定程度上依賴于背景和主題目標(biāo)的高對(duì)比度,因此在低對(duì)比度的環(huán)境下,可能會(huì)發(fā)生錯(cuò)誤匹配的情況. 而本方案依賴于矩形特征和對(duì)比度兩個(gè)方面,能有效地去除低對(duì)比度環(huán)境下的干擾.3.3 性能改進(jìn)

圖4 閾值分割法的裁剪結(jié)果

圖5 本文方法的裁剪結(jié)果

由于對(duì)一張圖像做Hough變換涉及逐像素進(jìn)行浮點(diǎn)運(yùn)算,其運(yùn)算過(guò)程所消耗的時(shí)間占處理圖像時(shí)間的極大比重. 而對(duì)圖像做Hough變換是為了得到圖像的量化結(jié)構(gòu)信息,因此Hough變換的結(jié)果只與圖像本身結(jié)構(gòu)有關(guān),與圖像分辨率無(wú)關(guān). 對(duì)于待處理圖像,本文將其以固定寬為100像素等比例壓縮. 對(duì)壓縮之后的縮略圖做Hough變換,所得到的量化結(jié)構(gòu)信息做矩形識(shí)別. 對(duì)識(shí)別出的裁剪框按照比例還原在原圖的位置,再對(duì)原圖進(jìn)行裁剪和傾斜校正. 表1和表2統(tǒng)計(jì)了對(duì)原圖以及縮略圖做識(shí)別所用的平均時(shí)間.

表1 處理原圖所用平均時(shí)間(單位： ms)

從表1和表2分析可以看出,使用縮略圖進(jìn)行處理,其算法的速度優(yōu)化明顯. 大量的逐像素運(yùn)算已經(jīng)不再成為性能瓶頸. 尤其是對(duì)較高分辨率的圖像,由于Hough變換與圖像大小無(wú)關(guān),因此處理時(shí)間減幅更大,使得實(shí)現(xiàn)實(shí)時(shí)票據(jù)裁剪和遠(yuǎn)程存儲(chǔ)成為可能.

表2 處理縮略圖所用平均時(shí)間(單位： ms)

4 結(jié)論與展望

本文針對(duì)銀行票據(jù)自動(dòng)裁剪應(yīng)用需求,基于窗口Hough變換和閾值分割,提出了自適應(yīng)Hough變換的矩形匹配和閾值二值分割算法. 窗口Hough變換對(duì)目標(biāo)的識(shí)別具有結(jié)構(gòu)約束,二值分割對(duì)目標(biāo)識(shí)別具有灰度對(duì)比約束,能夠最大可能降低光照對(duì)分割的不利影響. 在目前的50張實(shí)際拍攝銀行票據(jù)圖像的測(cè)試中,能通過(guò)97.5%的測(cè)試數(shù)據(jù). 反映出本算法的可靠性和穩(wěn)定性,具有推廣應(yīng)用價(jià)值.

1Lagunovsky D,Ablameyko S. Straight-line-based primitive extraction in grey-scale object recognition. Pattern Recognition Letters,1999,20(10)： 1005-1014. [doi： 10.1016/S0167-8655(99)00067-7]

2Lin CG,Nevatia R. Building detection and description from a single intensity image. Computer Vision and Image Understanding,1998,72(2)： 101-121. [doi： 10.1006/cviu.1998.0724]

3Jung CR,Schramm R. Rectangle detection based on a windowed Hough transform. Proceedings of the 17th Brazilian Symposium on Computer Graphics and Image Processing. Curitiba,Brazil. 2004. 113-120.

4Jundale TA,Hegadi RS. Skew detection and correction of Devanagari script using Hough transform. Procedia Computer Science,2015,(45)： 305-311. [doi： 10.1016/j.procs.2015.03.147]

5Illingworth J,Kittler J. A survey of the Hough transform.Computer Vision Graphics &Image Processing,1988,43(2)：280.

6Leavers VF. Survey： Which Hough transform? CVGIP：Image Understanding,1993,58(2)： 250-264. [doi： 10.1006/ciun.1993.1041]

7Furukawa Y,Shinagawa Y. Accurate and robust line segment extraction by analyzing distribution around peaks in Hough space. Computer Vision and Image Understanding,2003,92(1)： 1-25. [doi： 10.1016/j.cviu.2003.07.002]

8李牧,閆繼紅,李戈,等. 自適應(yīng)Canny算子邊緣檢測(cè)技術(shù).哈爾濱工程大學(xué)學(xué)報(bào),2007,28(9)： 1002-1007.

9韓思奇,王蕾. 圖像分割的閾值法綜述. 系統(tǒng)工程與電子技術(shù),2002,24(6)： 91-94,102.

10劉欣欣,李雪,王瓊. 基于灰度直方圖的多閾值分割法. 計(jì)算機(jī)應(yīng)用與軟件,2013,30(12)： 28-30,63. [doi： 10.3969/j.issn.1000-386x.2013.12.008]

11陳果,左洪福. 圖像閾值分割的兩種新技術(shù). 模式識(shí)別與人工智能,2002,15(4)： 468-473.

12Princen J,Illingworth J,Kittler J. A formal definition of the Hough Transform： Properties and relationships. Journal of Mathematical Imaging and Vision,1992,1(2)： 153-168.[doi： 10.1007/BF00122210]

13Duda RO,Hart PE. Use of the Hough transformation to detect lines and curves in pictures. Communications of the ACM,1972,15(1)： 11-15. [doi： 10.1145/361237.361242]

14Boukharouba A. A new algorithm for skew correction and baseline detection based on the randomized Hough transform.Journal of King Saud University-Computer and Information Sciences,2017,29(1)： 29-38. [doi： 10.1016/j.jksuci.2016.02.002]

15賀輝,劉琨,肖紅玉. 銀行票據(jù)自動(dòng)裁剪方案設(shè)計(jì)與控件開(kāi)發(fā). 計(jì)算機(jī)與數(shù)字工程,2016,45(7)： 1327-1332.

16陳強(qiáng),朱立新,夏德深. 結(jié)合Canny算子的圖像二值化. 計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào),2005,17(6)： 1302-1306.

17Shafii M,Sid-Ahmed M. Skew detection and correction based on an axes-parallel bounding box. International Journal on Document Analysis and Recognition,2015,18(1)： 59-71.[doi： 10.1007/s10032-014-0230-y]