改進蝙蝠算法在模糊層次分析中的應用①

張曉琪, 胡 振, 唐天國

(南充職業技術學院 信息與管理工程系,南充 637131)

蝙蝠算法(Bat Algorithm,BA)是劍橋大學的Xin-She Yang基于蝙蝠的回聲定位特性提出的一種群體智能搜索算法[1],它完美結合了現有成功算法的主要優點[2],具有模型簡單、求解效率高、潛在并行性和分布式等特點[3,4],其準確性和有效性優于遺傳算法(Genetic Algorithm,GA)、粒子群優化(Particle Swarm Optimization,PSO)算法等經典算法[5,6],已被應用于多個學科和工程領域[7-9]. 但BA沒有變異機制,難以保持種群的多樣性,容易陷入局部最優而發生早熟收斂,致使求解精度較低; 它比PSO算法加強了局部搜索,卻也引起了后期收斂速度變慢的問題. 為了改善性能,已研究出各種進化的、有效的變種蝙蝠算法[10],如： 劉長平等通過引入邏輯自映射函數改進局部搜索能力,提出了一種具有混沌搜索策略的蝙蝠優化算法[3,6]; 肖輝輝等將差分進化(Differential Evolution,DE)算法的變異、交叉和選擇機制融合到基本蝙蝠算法中,增強了種群的多樣性、全局尋優能力和搜索能力,形成了一種基于算法改進的蝙蝠算法[4]; 薛威力等通過動態調整參數和高斯擾動避免陷入局部最優,提出了一種基于方差改進的蝙蝠算法[10]. 這些改進策略能夠增強全局尋優能力、提高求解精度,但同時對算法的簡捷性和運行效率帶來了不利影響.

本文提出一種基于權重因子、Cauchy分布隨機數擾動和非線性規劃的改進蝙蝠算法,并將其應用于模糊層次分析中的判斷矩陣一致性修正與因素權重計算,取得了較為滿意的結果.

1 蝙蝠算法及其改進

1.1 基本蝙蝠算法

1.1.1 蝙蝠算法的仿生原理

BA是模擬自然界中蝙蝠利用超聲波來探測獵物、繞過障礙物的一種隨機搜索算法： 設有若干蝙蝠構成群體,其個體映射為多維空間中的可行解,將搜索最優解的過程模擬成蝙蝠個體移動和搜尋獵物過程;利用求解問題的適應度函數值衡量蝙蝠所處位置的優劣,將個體的優勝劣汰過程類比為優化過程中以較優的可行解替代較差可行解的迭代過程.

1.1.2 蝙蝠行為與算法描述

將蝙蝠的回聲定位行為按如下規則理想化：

(1) 所有蝙蝠利用超聲波回音的感覺差異來區分食物/獵物和障礙物.

(2) 每只蝙蝠以速度vi、固定頻率fmin(或波長λ)在位置xi(問題的解)隨機飛行. 在搜索獵物時,它們根據目標的遠近調整波長λ(或頻率f)、響度A和脈沖發射率r∈[0,1].

(3) 響度A從最大值A0(正數)以一定方式衰減到最小值Amin.

對于求解非線性最小值函數minfx,設蝙蝠群體規模為n,在d維搜索空間中,個體在t時刻的速度和位置分別為,則在(t+1)時刻其速度和位置更新為：

在優化過程中,當滿足條件時BA會自動轉為局部搜索,從當前最優解集中選擇一個解,并令每只蝙蝠在其鄰域隨機游走產生局部新解：

式中,x'是在當前最優解x附近產生的局部新解;ε∈[-1,1]為d維隨機向量;是蝙蝠群體在t時刻的平均響度.

蝙蝠在接近獵物的過程中,其脈沖發射速率ri逐步提高,同時聲波的響度Ai逐漸降低,并在發現獵物時達到最小. 相應迭代更新公式為：

1.2 蝙蝠算法的改進

與其它群體智能優化算法相似的是,BA也未能避免易陷入局部最優、發生早熟收斂等問題,因而對復雜高維多目標優化問題的求解精度不高. 究其原因,BA的尋優能力主要來自于蝙蝠個體間的相互作用,由于個體沒有變異機制,“超級蝙蝠”可能吸引其它個體迅速向其聚攏,致使種群多樣性嚴重下降; 同時,隨著蝙蝠個體在迭代過程中不斷移向最優個體,種群逐漸喪失進化能力,故而后期的收斂速度大為降低甚至停滯. 由此可見,對BA的改進應著眼于全程保持種群的多樣性,使其全局搜索能力和迭代后期的進化能力得以增強.

本文通過在BA中引入權重因子、Cauchy分布隨機數擾動和非線性規劃來改進其性能.

1.2.1 引入速度權重因子

PSO算法以慣性權重w控制粒子對原有速度的繼承性,其值較大則粒子多樣性好,算法的全局搜索能力強; 反之則粒子移動性減弱,局部搜索能力增強. 在實際應用中,通常令w在指定取值區間內線性遞減,使PSO算法由前期強調全局搜索逐步轉為后期重在局部搜索,從而提高其整體優化性能.

蝙蝠算法與粒子群算法同屬群智能優化算法,二者的數學模型相近,故其運行機制非常相似,前者強化了局部搜索能力,但可通過一定的參數設置演變為后者. 同時,兩種算法都存在早熟收斂、求解精度較低等問題,因而可采用某些相同的策略來進行改進. 為此,我們將PSO算法的慣性權重引入BA,即為蝙蝠的速度增加一個權重因子w,并令其在區間[wl,wu]線性遞減,則將式(2)變為如下式(6)：

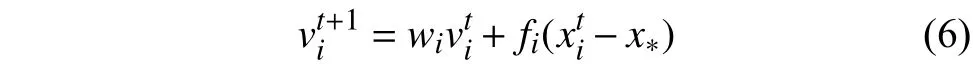
顯然,式(2)是w≡1時的一種特殊情況[11]. 每次迭代時,權重因子w按式(7)計算：

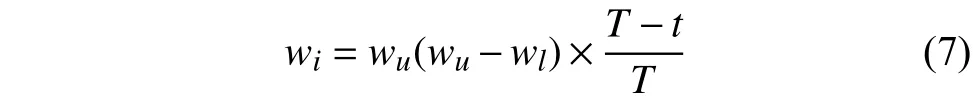
1.2.2 施加Cauchy分布隨機數擾動

Cauchy分布的概率特性是兩翼較長,易于產生遠離原點的隨機數. 因此,對蝙蝠位置進行Cauchy分布隨機數擾動,可較好地保持蝙蝠群體的多樣性,降低其陷入局部最優的概率,從而提高算法的全局搜索能力,有效防止早熟現象的發生. 擾動公式如下：

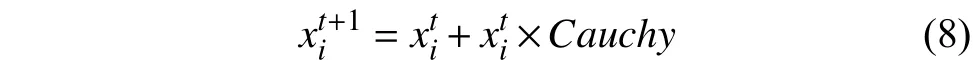
式中,Cauchy表示標準Cauchy分布隨機數,其值為,其中為均勻分布隨機數.

1.2.3 融入非線性規劃

將速度權重因子和Cauchy分布隨機數擾動引入BA,能改善其群體的多樣性,使其全局搜索能力得以提高,但也可能由于蝙蝠移動性的增強而錯過最佳解,為此在算法中融入非線性規劃函數,以提高其局部搜索效率和整體優化精度,并加快收斂速度.

非線性規劃(Nonlinear Programming,NP)研究n元實函數在一組等式或不等式約束條件下的極值問題,其目標函數和約束條件必有至少一個為未知量的非線性函數. 一般形式如下：

設計非線性規劃函數fnp(或直接使用MATLAB的fmincon函數),從變量的初始值開始搜索約束條件下的函數最小值,在BA尋優過程中調用之： 傳送x的當前值(蝙蝠位置)至fnp函數,以之為初始值進行最佳函數值的搜索,并將所得x的更好值返回BA繼續迭代過程. 為避免對算法的運行速度產生明顯影響,可根據優化問題的實際需要,每完成10次或20次迭代調用1次fnp函數.

1.3 改進蝙蝠算法的流程

(1) 設置算法參數. 確定蝙蝠數量n、變量維度d和最大迭代次數T,設置搜索脈沖頻率范圍[fmin,fmax]、脈沖速率最大值r0及其增強系數γ、響度最大值A0及其衰減系數α,給出變量空間[xl,xu]、蝙蝠速度范圍[vl,vu]及其權重取值區間[wl,wu];

(2) 隨機初始化蝙蝠位置xi、速度vi及搜索脈沖的頻率fi、速率ri和響度Ai,并根據適應度值找出當前最優個體位置x*;

(3) 根據式(1)更新脈沖頻率fi,依次由式(7)、式(6)計算蝙蝠的速度vi,再按式(3)更新其位置xi,即得新一代蝙蝠群體;

(4) 若隨機數rand>ri,則利用式(4)對當前最優蝙蝠位置進行隨機擾動,以擾動結果替換當前蝙蝠個體位置,并計算其適應度值;

(5) 若蝙蝠位置得到改善且rand＜Ai,則接受所得新解,并按式(5)更新脈沖響度Ai和發射速率ri. 否則按式(8)對蝙蝠位置施加Cauchy分布隨機數擾動,并進行越界處理;

(6) 根據適應度值找出蝙蝠群體的當前最優解和最優值;

(7) 若迭代次數t為20(或10)的倍數,則調用非線性規劃函數fnp加強局部搜索;

(8) 若達到最大迭代次數T(或優化精度ε),停止搜索并輸出全局最優解和最優值,否則轉到步驟(3)進入下一次迭代.

1.4 改進蝙蝠算法的測試

采用標準測試函數,在32位Windows7系統環境用MATLAB R2015b編程運行. 為了方便敘述和比較分析,將僅引入速度權重和Cauchy分布隨機數擾動的蝙蝠算法稱為WCBA,而將在此基礎上融入非線性規劃的改進算法簡稱WCNBA.

1.4.1 測試函數及參數設置

選用5個標準測試函數,其屬性如表1所示.

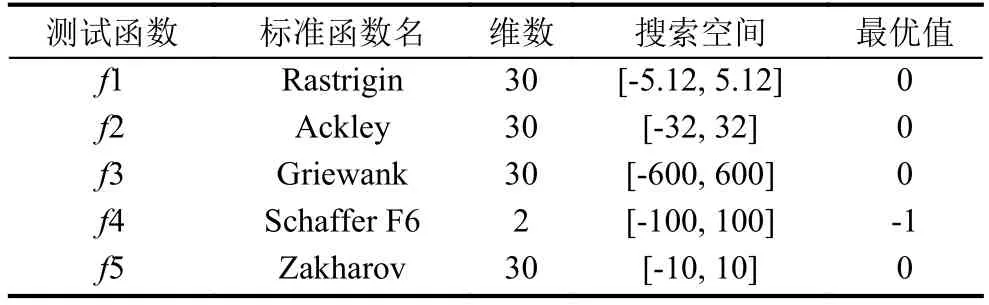
表1 5個測試函數

由于測試目的是將WCBA和WCNBA與BA進行比較,以驗證改進的有效性,因此沒有刻意對算法的參數進行優化,而是統一設置為：n=40,T=300;fi∈[-1,1],r0=0.75,A0=0.25,γ=α=0.9;vi∈[-1,1],wi∈[1.0,0.5].

同時,我們也選取兩種經典算法DE和PSO對一些函數進行測試,以便進一步對蝙蝠算法及其改進效果進行對比分析. DE算法參數： 縮放因子F0=0.5,交叉概率CR=0.25; PSO算法參數： 學習因子c1=c2=2.05,速度取值區間v∈[-1,1]. 結果表明,BA、WCBA和WCNBA全面優于DE和PSO算法,其中單峰函數Sphere與多峰函數Rastrigin的求解迭代曲線分別如圖1、圖2所示.

圖1 Sphere函數的求解迭代曲線

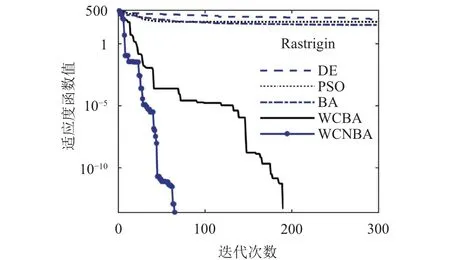
圖2 Rastrigin函數的求解迭代曲線

1.4.2 測試結果分析

每個測試函數獨立運行30次,取最優值、最差值、平均值和尋優成功率(獲得理論最優值的次數占獨立運行總次數的比率)進行比較,所得結果如表2所示.

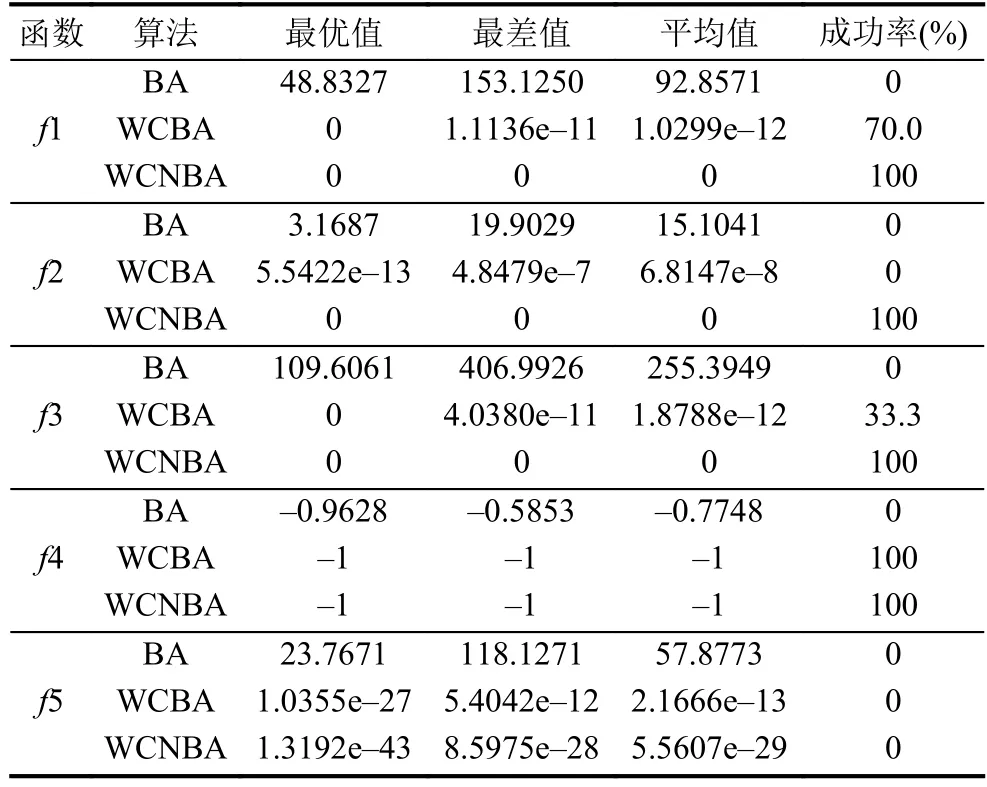
表2 標準函數測試結果

從表2的測試結果看,基于BA改進的WCBA和WCNBA皆顯著優于基本蝙蝠算法. 其中,WCNBA對f1～f4都能完全收斂到理論最優值,尋優成功率達到100%; 對于f5所得結果的平均值也非常接近理論最優值. 而WCBA對f4可完全收斂于理論最優值,對f1和f3的尋優成功率則分別達到70.0%和33.3%,對f2和f5所得結果也遠優于BA. 因此,WCNBA是一種成功的BA改進算法,WCBA也具有一定的實用價值.

2 改進蝙蝠算法在模糊層次分析中的應用

2.1 模糊層次分析的步驟與關鍵環節

層次分析法(Analytic Hierarchy Process,AHP)是將決策問題作為一個系統,將其影響因素分解為目標、準則和方案等層次,在此基礎上將定性指標模糊量化,遵照人類的思維、判斷規律進行決策過程的一種實用方法. 因在處理復雜決策問題方面的實用性和有效性,AHP廣泛應用于眾多領域.

將AHP應用于模糊環境即為模糊層次分析法(Fuzzy Analytic Hierarchy Process,FAHP),它應用模糊數學的隸屬度來量化指標實測值,從而解決層次分析中的模糊性(如因素類屬之間不明晰、專家認識上的模糊性等)問題,最大限度地降低人為因素的影響.FAHP的主要步驟為：

(2) 確定各層因素分別對其直接上級重要程度兩兩比較的隸屬度,以之建立模糊互補矩陣;

(3) 層次單排序(計算各層因素的相對權重);

(4) 方案總排序(方案層對目標層的合成權重).

模糊層次分析的數據量大、計算復雜繁瑣,其關鍵環節為計算因素權重,它決定了決策結果的科學性、合理性和可信度. 計算因素權重的必要條件是模糊互補矩陣具有滿意一致性,因此還需先對其進行一致性檢驗和修正.

2.2 用改進蝙蝠算法求解因素權重

對于模糊互補矩陣M=(mij)n×n(n為因素個數)：

（一）從政治意義看，習近平新時代中國特色社會主義思想，是新時代國家政治生活和社會生活的根本指針。從政黨發展史看，擁有堅強的領導核心，擁有科學的指導思想，是一個政黨形成凝聚力戰斗力不可或缺的兩個方面，也是政黨走向成熟的重要標志。我們黨確立習近平新時代中國特色社會主義思想的指導地位，確立習近平總書記的核心地位，對于維護黨中央權威和集中統一領導，對于保證黨和國家事業興旺發達、長治久安具有重大而深遠的意義，標志著我們這個走過97年光輝歷程的世界第一大黨，達到了政治上、思想上、組織上的空前團結和統一，為推進新時代中國特色社會主義事業提供了堅強政治保障。

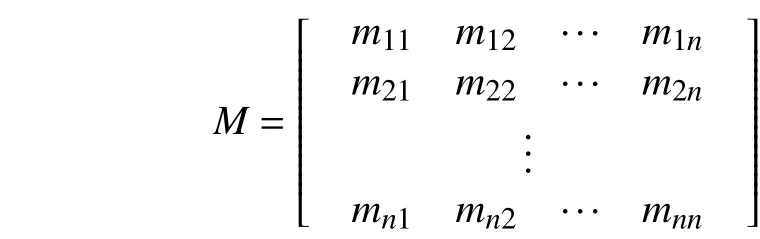
以0.1～0.9標度法表示其元素值,則由模糊互補矩陣的定義可知：mii=0.5、mij+mji=1(i,j=1,2,…,n分別為元素mij的行號和列號),亦即M的對角線元素恒為0.5、其左下區域元素mji=1-mij. 因此,在應用中只需確定右上區域元素mij,即可算得左下區域元素mji.

傳統做法是先用手工調整或數學變換法進行模糊互補矩陣的一致性檢驗與修正,再以方根法、特征值法、和行歸一化法和排序法等由模糊互補一致性矩陣計算因素權重,其計算量大、繁瑣費時. 應用WCNBA可將這兩步工作合二為一,即同時完成模糊互補矩陣的一致性檢驗、修正和相應的因素權重計算,從而簡化步驟、提高效率.

2.2.1 模糊互補一致性矩陣的充要條件

定義1. 對于模糊互補矩陣M=(mij)n×n,若,都有：

則稱M為加性一致性模糊互補矩陣. 由此可推知模糊互補一致性矩陣的充要條件為： 任意指定行與其余各行對應元素之差為某一常數.

定理1. 設M=(mij)n×n為模糊互補矩陣,則M是模糊一致性矩陣的充要條件為： 存在一階非負歸一化向量及正數α,使得,皆有

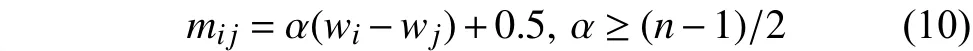
式中,α是對因素之間重視程度差異的度量,其值小則決策者越重視這種差異;wi為因素權重.

2.2.2 用改進蝙蝠算法求解因素權重

設R=(rij)n×n為修正后的模糊互補矩陣,將式(9)的推論和式(10)結合起來,可得模糊互補矩陣一致性的指標函數：

該指標函數值越小,則R的一致性越好; 其值為0時,R具有完全一致性. 在實際應用中,通常以f(n)＜0.1為模糊互補矩陣具有滿意一致性的標準.

應用WCNBA同步進行模糊互補矩陣的一致性修正和因素權重計算時,以因素權重及矩陣右上區域(不含對角線)除第一行之外的元素為優化變量(共有(n-1)(n-2)/2+n個,n為因素個數),以實數形式編碼,并設其搜索區間為[0,1]; 以式(11)為適應度函數進行搜索,當其值＜0.1或達到最大迭代次數時,返回因素權重和修正后的元素值.

2.2.3 應用實例

在某校的課程建設質量評價中,采用模糊層次分析法確定各級評價指標的主觀權重,其中有如下兩個模糊互補矩陣[13]：

用WCNBA進行M1、M2的一致性修正和因素權重計算,算法的運行參數均按1.4.1設置,其尋優迭代過程如圖3所示,所得結果如表3所示.

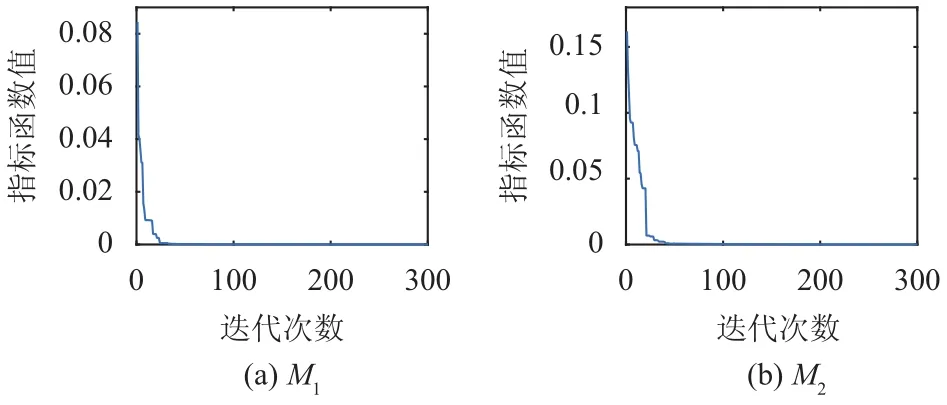
圖3 用WCNBA對M1、M2的尋優迭代過程

將表3與M1、M2的數據對比可知,M1的(2,4)和M2的(2,3)、(3,5)位置處的元素得到了修正,于是相應的模糊互補一致性矩陣R1和R2如下：

表3 M1、M2的一致性修正和因素權重計算結果

3 結論

本文針對基本蝙蝠算法在尋優過程中難以保持種群的多樣性、易發生早熟收斂、求解精度較低等問題,通過引入速度權重因子、施加Cauchy分布隨機數擾動和融入非線性規劃函數等措施,設計并實現了改進的蝙蝠算法WCBA和WCNBA. 經用標準函數測試,并在模糊層次分析中應用,結果表明改進的蝙蝠算法顯著優于基本蝙蝠算法.

1Yang XS. A new metaheuristic bat-inspired algorithm.González JR,Pelta DA,Cruz C,et al. Nature Inspired Cooperative Strategies for Optimization. Berlin Heidelberg：Springer,2010. 65-74.

2李煜,馬良. 新型全局優化蝙蝠算法. 計算機科學,2013,40(9)： 225-229.

3劉長平,葉春明. 具有混沌搜索策略的蝙蝠優化算法及性能仿真. 系統仿真學報,2013,25(6)： 1183-1188,1195.

4肖輝輝,段艷明. 基于DE算法改進的蝙蝠算法的研究及應用. 計算機仿真,2014,31(1)： 272-277,301.

5賀興時,丁文靜,楊新社. 基于模擬退火高斯擾動的蝙蝠優化算法. 計算機應用研究,2014,31(2)： 392-397.

6劉長平,葉春明,劉滿成. 來自大自然的尋優策略： 像蝙蝠一樣感知. 計算機應用研究,2013,30(5)： 1320-1322,1356.

7盛曉華,葉春明. 蝙蝠算法在PFSP調度問題中的應用研究. 工業工程,2013,16(1)： 119-124.

8李枝勇,馬良,張惠珍. 0-1規劃問題的元胞蝙蝠算法. 計算機應用研究,2013,30(10)： 2903-2906,2935. [doi： 10.3969/j.issn.1001-3695.2013.10.005]

9張蓉. 蝙蝠算法優化最二乘支持向量機的網絡入侵檢測.激光雜志,2014,35(11)： 101-104.

10薛威力,賀興時,楊新社. 蝙蝠算法的一種改進. 哈爾濱商業大學學報(自然科學版),2016,32(6)： 706-712.

11李枝勇,馬良,張惠珍. 蝙蝠算法收斂性分析. 數學的實踐與認識,2013,43(12)： 182-190. [doi： 10.3969/j.issn.1000-0984.2013.12.026]

12胡振. QPSO混合算法在PID控制器優化中的應用. 計算機系統應用,2014,23(10)： 233-238. [doi： 10.3969/j.issn.1003-3254.2014.10.042]

13陳素彬,胡振. 高職院校分析化學課程建設的量化評價方法. 化學教育,2017,38(8)： 44-50.